openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复
文章目录
- openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复
- 152.1 背景信息
- 152.2 前提条件
- 152.3 PITR恢复流程
- 152.4 recovery.conf文件配置
- **152.4.1 归档恢复配置**
- **152.4.2 恢复目标设置**
openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复
152.1 背景信息
当数据库崩溃或希望回退到数据库之前的某一状态时,openGauss的即时恢复功能(Point-In-Time Recovery,简称PITR)可以支持恢复到备份归档数据之后的任意时间点。
说明:
- PITR仅支持恢复到物理备份数据之后的某一时间点。
- 仅主节点可以进行PITR恢复,备机需要进行全量build达成与主机数据同步。
152.2 前提条件
- 基于经过物理备份的全量数据文件。
- 基于已归档的WAL日志文件。
152.3 PITR恢复流程
- 将物理备份的文件替换目标数据库目录。
- 删除数据库目录下pg_xlog/中的所有文件。
- 将归档的WAL日志文件复制到pg_xlog文件中(此步骤可以省略,通过配置recovery.conf恢复命令文件中的restore_command项替代)。
- 在数据库目录下创建恢复命令文件recovery.conf,指定数据库恢复的程度。
- 启动数据库。
- 连接数据库,查看是否恢复到希望预期的状态。
- 若已经恢复到预期状态,通过pg_xlog_replay_resume()指令使主节点对外提供服务。
152.4 recovery.conf文件配置
152.4.1 归档恢复配置
- restore_command = string
这个SHELL命令是获取WAL文件系列中已归档的WAL文件。字符串中的任何一个%f是用归档检索中的文件名替换, 并且%p是用服务器上的复制目的地的路径名替换。 任意一个%r是用包含最新可用重启点的文件名替换。
示例:
restore_command = 'cp /mnt/server/archivedir/%f %p'
- archive_cleanup_command = string
这个选项参数声明一个shell命令。在每次重启时会执行这个shell命令。 archive_cleanup_command为清理备库不需要的归档WAL文件提供一个机制。 任何一个%r由包含最新可用重启点的文件名代替。这是最早的文件,因此必须保留以允许恢复能够重新启动,因此所有早于%r的文件可以安全的移除。
示例:
archive_cleanup_command = 'pg_archivecleanup /mnt/server/archivedir %r'
需要注意的是,如果多个备服务器从相同的归档路径恢复时, 需要确保在任何一个备服务器在需要之前,不能删除WAL文件。
- recovery_end_command = string
这个参数是可选的,用于声明一个只在恢复完成时执行的SHELL命令。recovery_end_command是为以后的复制或恢复提供一个清理机制。
152.4.2 恢复目标设置
- recovery_target_name = string
此参数声明命名还原到一个使用pg_create_restore_point()创建的还原点。
示例:
recovery_target_name = 'restore_point_1'
- recovery_target_time = timestamp
此参数声明命名还原到一个指定时间戳。
示例:
recovery_target_time = '2020-01-01 12:00:00'
- recovery_target_xid = string
这个参数声明还原到一个事务ID。
示例:
recovery_target_xid = '3000'
- recovery_target_lsn = string
这个参数声明还原到日志的指定LSN点。
示例:
recovery_target_lsn = '0/0FFFFFF'
- recovery_target_inclusive = boolean
声明是否在指定恢复目标(true)之后停止,或在这(false)之前停止。改声明仅支持恢复目标为recovery_target_time、recovery_target_xid和recovery_target_lsn的配置。
示例:
recovery_target_inclusive = true
 说明:
说明:
- recovery_target_name、recovery_target_time、recovery_target_xid、recovery_target_lsn这四个配置项仅同时支持一项。
- 如果不配置任何恢复目标,或配置目标不存在,则默认恢复到最新的WAL日志点。
👍 点赞,你的认可是我创作的动力!
⭐️ 收藏,你的青睐是我努力的方向!
✏️ 评论,你的意见是我进步的财富!

相关文章:

openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复
文章目录 openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复152.1 背景信息152.2 前提条件152.3 PITR恢复流程152.4 recovery.conf文件配置**152.4.1 归档恢复配置****152.4.2 恢复目标设置** openGauss学习笔记-152 openGauss 数据库运维-备份…...
PhpStorm基本配置及常用快捷键
重要Preference配置 激活服务器 http://jetbrains.tencent.click/http://owo.helphttp://idea.imsxm.com/http://www.0-php.com:10172017.3以上版本 JetBrains IDE 2017.3以上版本,激活检测机制变成了动态封禁域名,导致大部分域名激活被屏蔽了࿰…...

Autosar通信实战系列05-CanNM模块进阶常见问题思考
本文框架 前言1. UDS 0x28服务控制Nm报文收发后对状态机有影响?2. 节点网络启动后第一帧是否必须是网络管理报文?3. 主动唤醒后发送的第一帧报文为NM报文如何配置?4. CanNmMsgCycleOffset的使用场景?5. 什么情况下CBV中RepeatMessageRequest Bit置位?6. 主动(本地)唤醒与…...

Java中多态的一些简单理解
什么是多态 1.面向对象的三大特性:封装、继承、多态。从一定角度来看,封装和继承几乎都是为多态而准备的。这是我们最后一个概念,也是最重要的知识点。 2.多态的定义:指允许不同类的对象对同一消息做出响应。即同一消息可以根据发…...
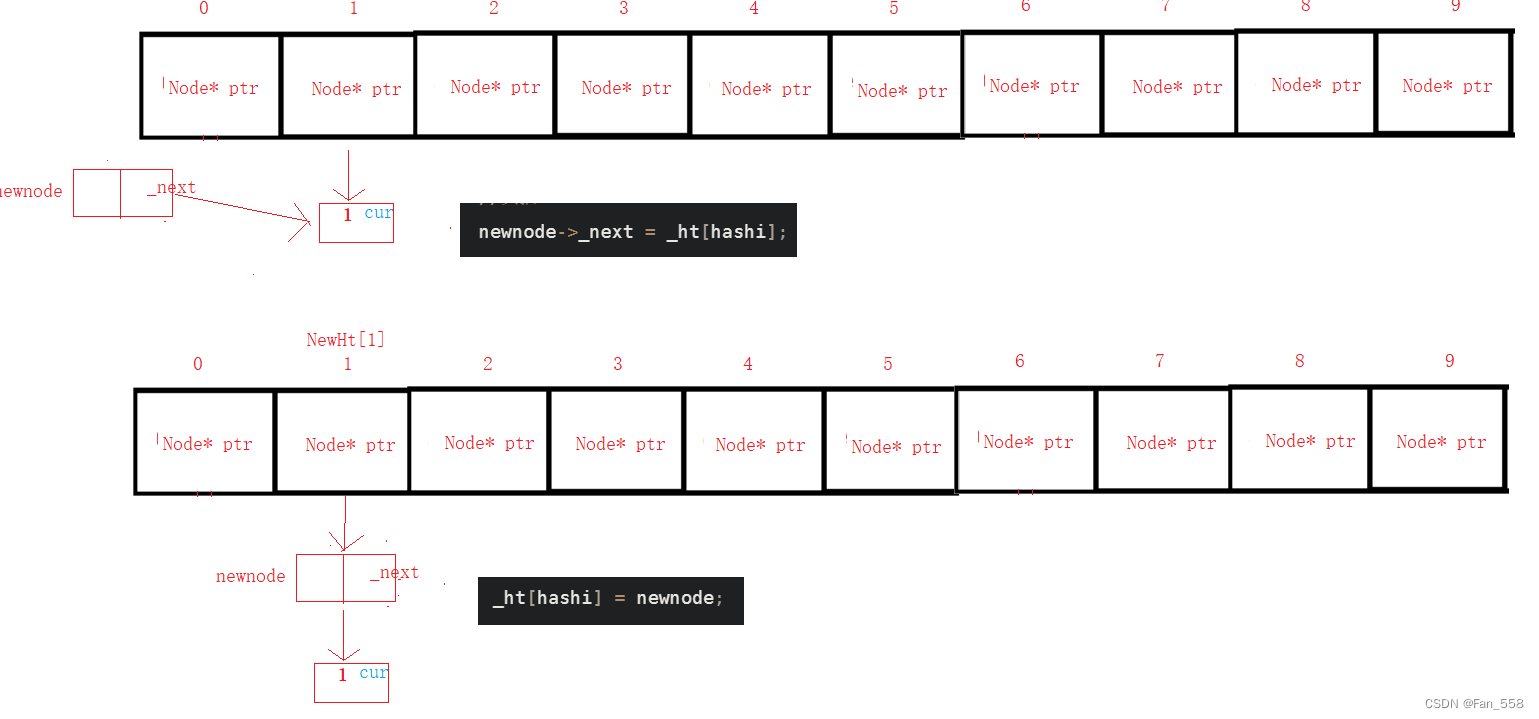
011 数据结构_哈希
前言 本文将会向你介绍哈希概念,哈希方法,如何解决哈希冲突,以及闭散列与开散列的模拟实现 1. 哈希概念 顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素时,必须要经…...
案例025:基于微信小程序的移动学习平台的设计与实现
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...
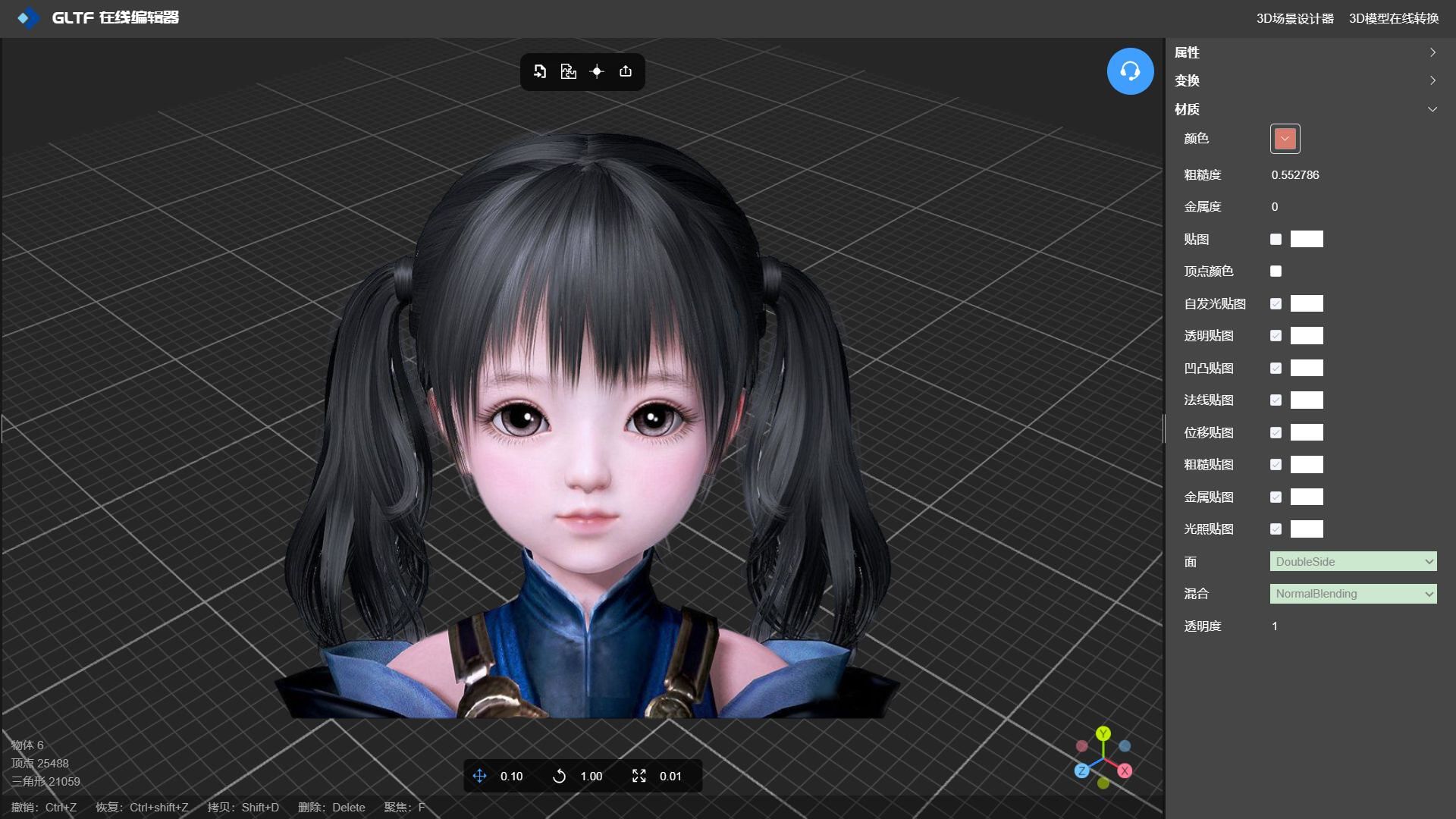
写实3D游戏模型纹理贴图设置
在线工具推荐: 3D数字孪生场景编辑器 - GLTF/GLB材质纹理 - 3D模型在线转换 - Three.js AI自动纹理开发包 - YOLO 虚幻合成数据生成器 - 三维模型预览图生成器 - 3D模型语义搜索引擎 当谈到游戏角色的3D模型风格时,有几种不同的风格: …...

如何基于Akamai IoT边缘平台打造一个无服务器的位置分享应用
与地理位置有关的应用相信大家都很熟悉了,无论是IM软件里的位置共享或是电商、外卖应用中的配送地址匹配,我们几乎每天都在使用类似的功能与服务。不过你有没有想过,如何在自己开发的应用中嵌入类似的功能? 本文Akamai将为大家提…...

【开源】基于JAVA的木马文件检测系统
项目编号: S 041 ,文末获取源码。 \color{red}{项目编号:S041,文末获取源码。} 项目编号:S041,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 木马分类模块2.3 木…...
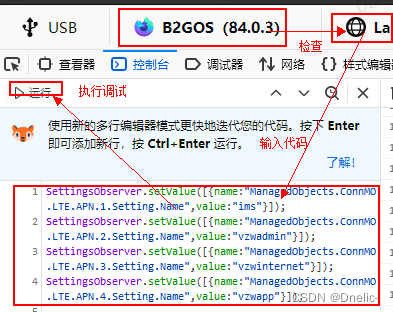
KaiOS 运营商相关文件operator_variant_manager.js代码功能和调试
gaia/apps/system/js/operator_variant_manager.js at master mozilla-b2g/gaia GitHub js文件接口功能 No 接口/常量 功能 1 OperatorVariantManager var OperatorVariantManager function(core) 2 OperatorVariantManager.IMPORTS OperatorVariantManager.I…...
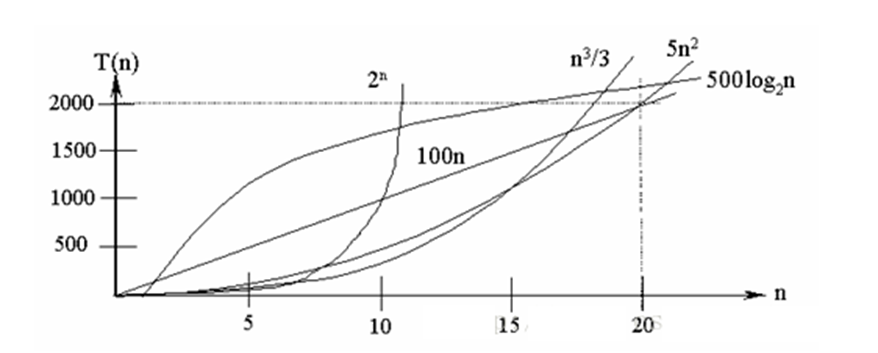
【数据结构(六)】排序算法介绍和算法的复杂度计算(1)
文章目录 1. 排序算法的介绍1.1. 排序的分类 2. 算法的时间复杂度2.1. 度量一个程序(算法)执行时间的两种方法2.2. 时间频度2.2.1. 忽略常数项2.2.2. 忽略低次项2.2.2. 忽略系数 2.3. 时间复杂度2.4. 常见的时间复杂度2.5. 平均时间复杂度和最坏时间复杂度 3. 算法的空间复杂度…...

带有 RaspiCam 的 Raspberry Pi 监控和延时摄影摄像机
一、说明 一段时间以来,我一直想构建一个运动激活且具有延时功能的树莓派相机,但从未真正找到我喜欢的案例。我在thingiverse上找到了这个适合树莓派和相机的好案例。它是为特定的鱼眼相机设计的,但从模型来看,我拥有的廉价中国鱼…...
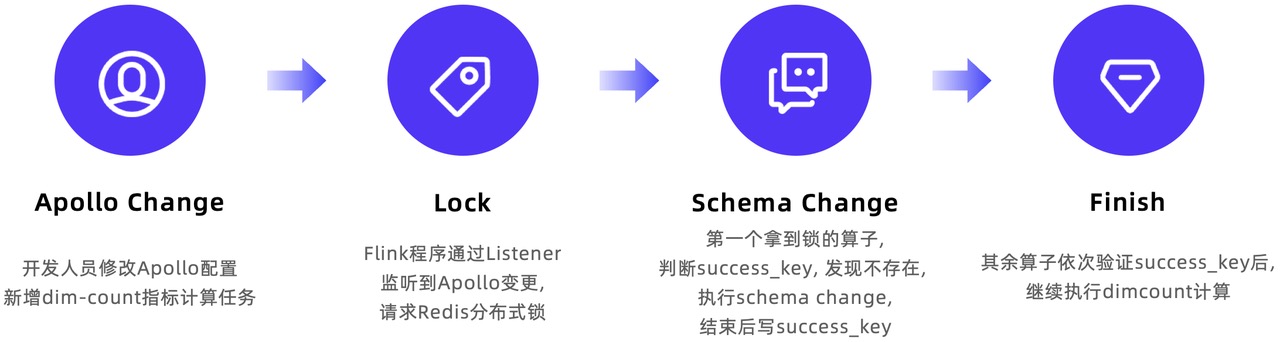
Apache Doris 在某工商信息商业查询平台的湖仓一体建设实践
作者|某工商信息商业查询平台 高级数据研发工程师 李昂 信息服务行业可以提供多样化、便捷、高效、安全的信息化服务,为个人及商业决策提供了重要支撑与参考。对于行业相关企业来说,数据收集、加工、分析能力的重要性不言而喻。以某工商信息…...

【尘缘送书第六期】2023年度学习:AIGC、AGI、GhatGPT、人工智能大模型实现必读书单
【文末送书】今天推荐几本AIGC、AGI、GhatGPT、人工智能大模型领域优质书籍。 目录 前言1 《ChatGPT 驱动软件开发》2 《ChatGPT原理与实战》3 《神经网络与深度学习》4 《AIGC重塑教育》5 《通用人工智能》6 文末送书 前言 2023年是人工智能大语言模型大爆发的一年࿰…...
我的 CSDN 三周年创作纪念日:2020-12-12
本人大叔一枚,自1992年接触电脑,持续了30年的业余电脑发烧爱好者,2022年CSDN博客之星Top58,阿里云社区“乘风者计划”专家博主。自某不知名财校毕业后进入国有大行工作至今,先后任职于某分行信息科技部、电子银行部、金…...

什么是css初始化
什么是css初始化 CSS初始化是指重设浏览器的样式。 因为浏览器的兼容问题,不同浏览器对有些标签的默认值是不同的,如果没对CSS初始化往往会出现浏览器之间的页面显示差异。 每次新开发网站或新网页时候通过初始化CSS样式的属性,为我们将用…...

谁会成为第一个MoE大模型基座呢?重磅!Mixtral MoE 8x7B!!!
文章目录 谁会成为第一个MoE大模型基座呢?重磅!Mixtral MoE 8x7B!!!前言重磅!Mixtral MoE 8x7B!!!Mixtral是啥模型介绍模型结构长啥样?表现如何?可…...

Linux升级nginx版本
处于漏洞修复目的服务器所用nginx是1.16.0版本扫出来存在安全隐患,需要我们升级到1.17.7以上。 一般nginx默认在 /usr/local/ 目录,这里我的nginx是自定义的路径安装在 /app/weblogic/nginx 。 1.查看生产环境nginx版本 cd /app/weblogic/nginx/sbin/…...
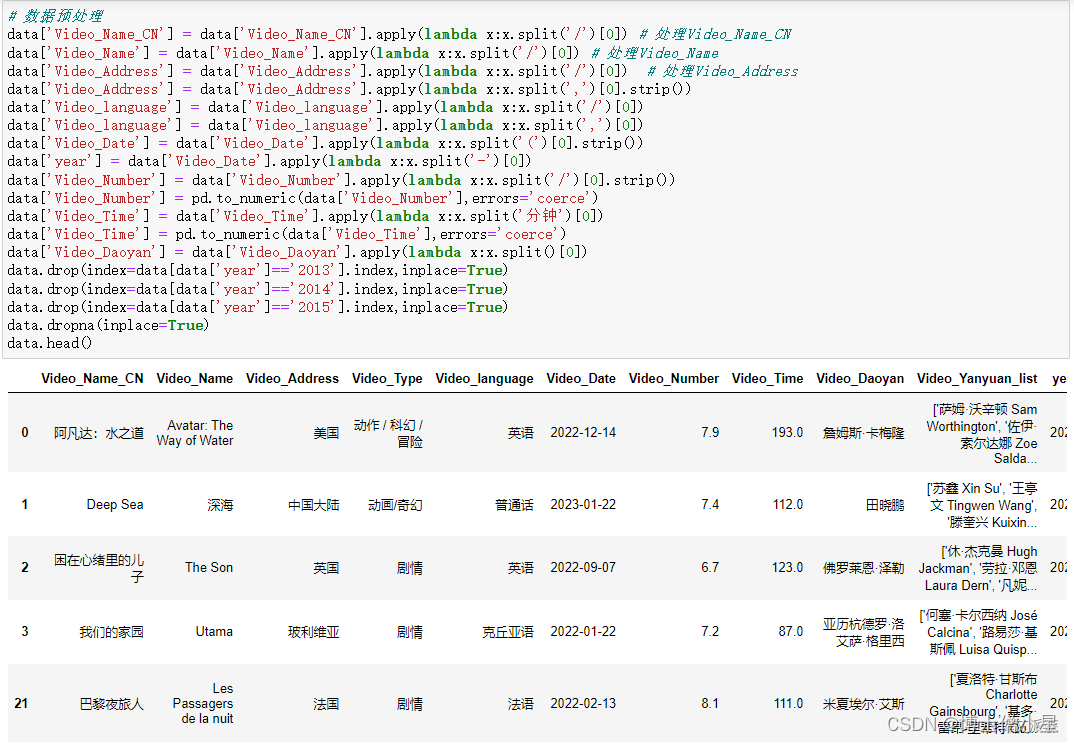
人工智能|网络爬虫——用Python爬取电影数据并可视化分析
一、获取数据 1.技术工具 IDE编辑器:vscode 发送请求:requests 解析工具:xpath def Get_Detail(Details_Url):Detail_Url Base_Url Details_UrlOne_Detail requests.get(urlDetail_Url, headersHeaders)One_Detail_Html One_Detail.cont…...

mac苹果笔记本电脑如何强力删除卸载app软件?
苹果电脑怎样删除app?不是把app移到废纸篓就行了吗,十分简单呢! 其实不然,因为在Mac电脑上,删除应用程序只是删除了应用程序的主要组件。大多数时候,系统会有一个相当长的目录,包含所有与应用程…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
