70.爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意: 给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
解题思路
动态规划
- 定义状态: 设
dp[i]表示爬到第i阶楼梯的方法数。 - 状态转移方程:
dp[i] = dp[i-1] + dp[i-2],即爬到第i阶楼梯的方法数等于爬到第i-1阶楼梯的方法数加上爬到第i-2阶楼梯的方法数。 - 初始状态:
dp[1] = 1,dp[2] = 2。 - 遍历顺序: 从小到大遍历,计算每一层楼梯的方法数。
特殊案例
- 如果输入
n为 1 或 2,则直接返回n。
C#代码实现
public int ClimbStairs(int n) {// 如果楼梯只有一阶或者两阶,直接返回阶数if (n == 1 || n == 2) {return n;}// 创建一个数组,长度为n+1int[] dp = new int[n + 1];// 初始化数组,第一阶和第二阶的步数都为1dp[1] = 1;dp[2] = 2;// 从第三阶开始,动态规划计算步数for (int i = 3; i <= n; i++) {// 动态规划转移方程,dp[i] = dp[i - 1] + dp[i - 2]dp[i] = dp[i - 1] + dp[i - 2];}// 返回最后一步的步数return dp[n];
}
C代码实现
int climbStairs(int n) {// 如果楼梯只有一阶或者两阶,直接返回阶数if (n == 1 || n == 2) {return n;}// 定义一个数组,用来存储阶数对应的斐波那契数int* dp = (int*)malloc(sizeof(int) * (n + 1));// 初始化数组,斐波那契数从1开始,所以dp[1]和dp[2]都等于1dp[1] = 1;dp[2] = 2;// 从第三阶开始,斐波那契数等于前两阶的和for (int i = 3; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}// 返回斐波那契数int result = dp[n];// 释放内存free(dp);return result;
}
时间复杂度和空间复杂度
- 时间复杂度:O(n),其中 n 是楼梯的阶数。需要计算每一层楼梯的方法数。
- 空间复杂度:O(n)。使用了一个大小为 n+1 的数组来保存中间结果。
相关文章:

70.爬楼梯
题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意: 给定 n 是一个正整数。 示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶…...

【论文解读】ICLR 2024高分作:ViT需要寄存器
来源:投稿 作者:橡皮 编辑:学姐 论文链接:https://arxiv.org/abs/2309.16588 摘要: Transformer最近已成为学习视觉表示的强大工具。在本文中,我们识别并表征监督和自监督 ViT 网络的特征图中的伪影。这些…...
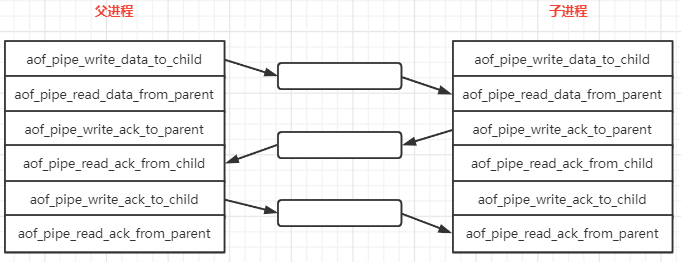
【Redis】AOF 基础
因为 Redis AOF 的实现有些绕, 就分成 2 篇进行分析, 本篇主要是介绍一下 AOF 的一些特性和依赖的其他函数的逻辑,为下一篇 (Redis AOF 源码) 源码分析做一些铺垫。 AOF 全称: Append Only File, 是 Redis 提供了一种数据保存模式, Redis 默认不开启。 AOF 采用日志的形式来记…...
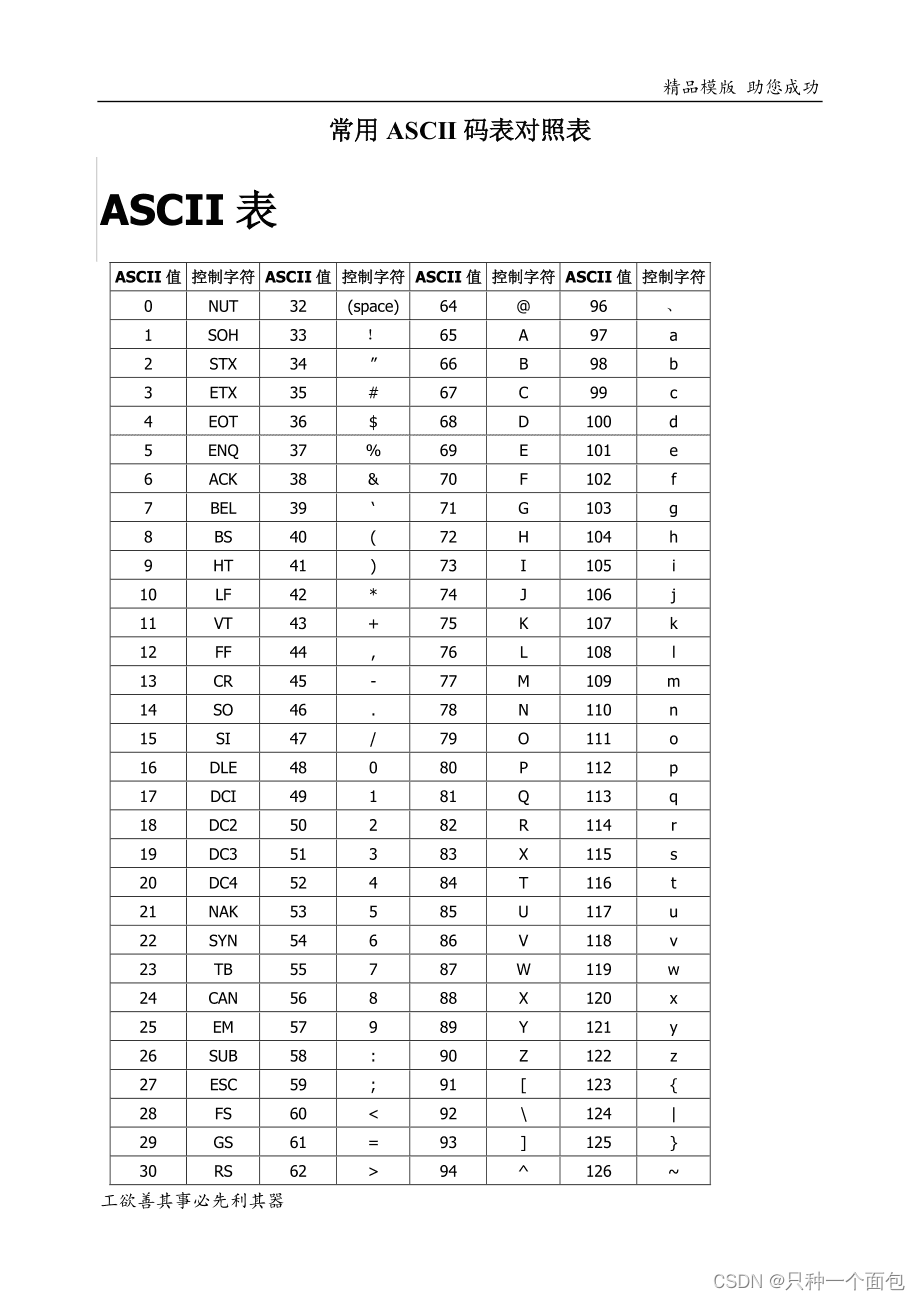
C语言—每日选择题—Day50
一天一天的更新,也是达到50天了,精选的题有250道,博主累计做了不下500道选择题,最喜欢的题型就是指针和数组之间的计算呀,不知道关注我的小伙伴是不是一直在坚持呢?文末有投票,大家可以投票让博…...
[C/C++]——内存管理
学习C/C的内存管理 前言:一、C/C的内存分布二、C语言中动态内存管理方式三、C中动态内存管理方式3.1、new/delete操作符3.1.2、new/delete操作内置类型3.1.3、new/delete操作自定义类型 3.2、认识operator new和operator delete函数3.3、了解new和delete的实现原理3…...
PDF文件的限制编辑,如何设置?
想要给PDF文件设置一个密码防止他人对文件进行编辑,那么我们可以对PDF文件设置限制编辑,设置方法很简单,我们在PDF编辑器中点击文件 – 属性 – 安全,在权限下拉框中选中【密码保护】 然后在密码保护界面中,我们勾选【…...
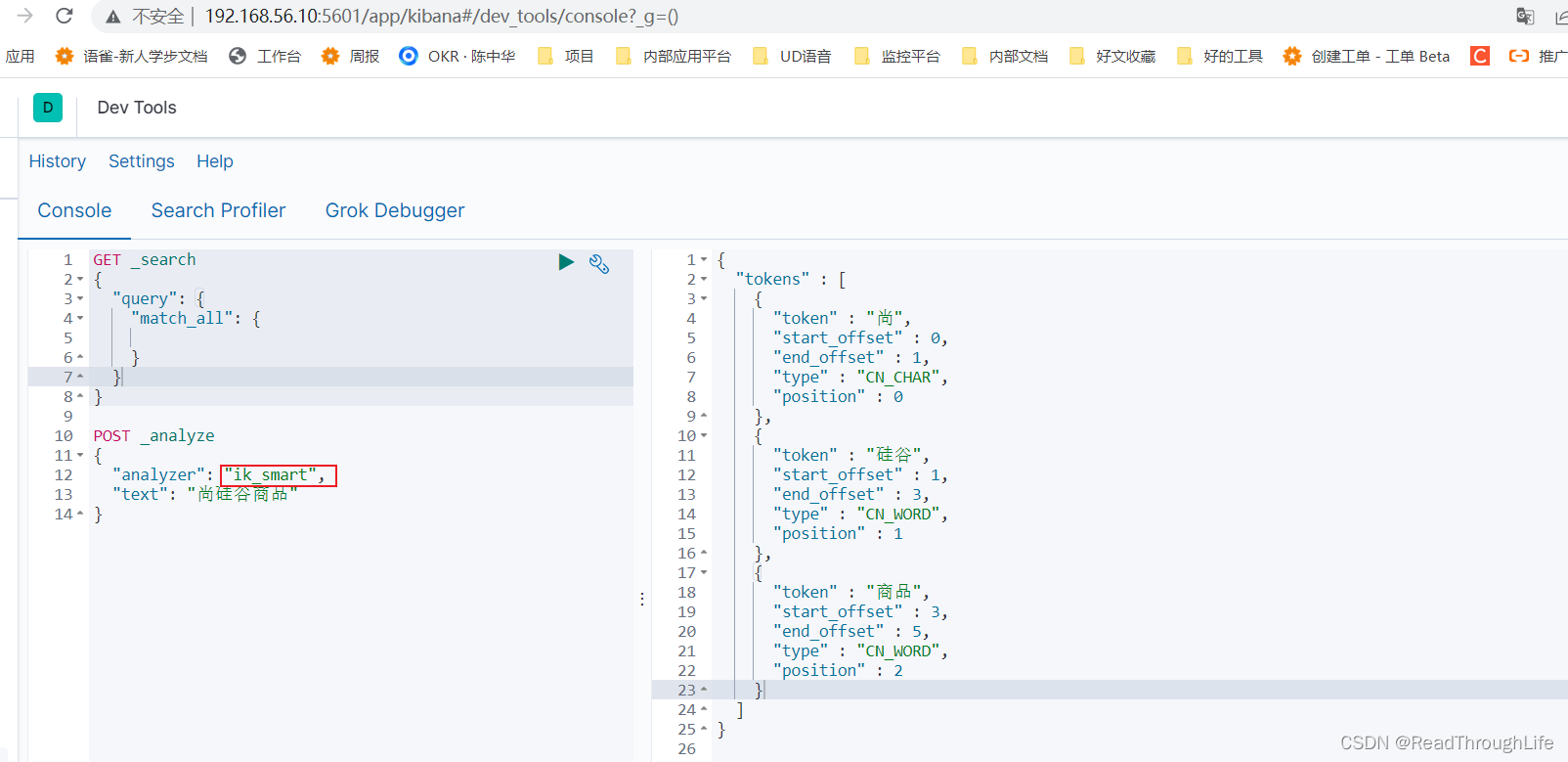
Linux 中使用 docker 安装 Elasticsearch 及 Kibana
Linux 中使用 docker 安装 Elasticsearch 及 Kibana 安装 Elasticsearch 和 Kibana安装分词插件 ik_smart 安装 Elasticsearch 和 Kibana 查看当前运行的镜像及本地已经下载的镜像,确认之前没有安装过 ES 和 Kibana 镜像 docker ps docker images从远程镜像仓库拉…...

在Flutter中使用PhotoViewGallery指南
介绍 Flutter中的PhotoViewGallery是一个功能强大的插件,用于在应用中展示可缩放的图片。无论是构建图像浏览器、相册应用,还是需要在应用中查看大图的场景,PhotoViewGallery都是一个不错的选择。 添加依赖 首先,需要在pubspec…...

c语言中的static静态(1)static修饰局部变量
#include<stdio.h> void test() {static int i 1;i;printf("%d ", i); } int main() {int j 0;while (j < 5){test();j j 1;}return 0; } 在上面的代码中,static修饰局部变量。 当用static定义一个局部变量后,这时局部变量就是…...

生信算法4 - 获取overlap序列索引和序列的算法
生信序列基本操作算法 建议在Jupyter实践,python版本3.9 1. 获取overlap序列索引和序列的算法实现 # min_length 最小overlap碱基数量3个 def getOverlapIndexAndSequence(a, b, min_length3):""" Return length of longest suffix of a matching…...

springboot 学习网站
Spring Boot 系列教程https://www.docs4dev.com/ Spring Boot 教程汇总 http://www.springboot.wiki/ Spring Cloud 微服务教程 http://www.springboot.wiki/ 1、自定义banner https://www.cnblogs.com/cc11001100/p/7456145.html 2、事件和监听器 https://blog.csd…...
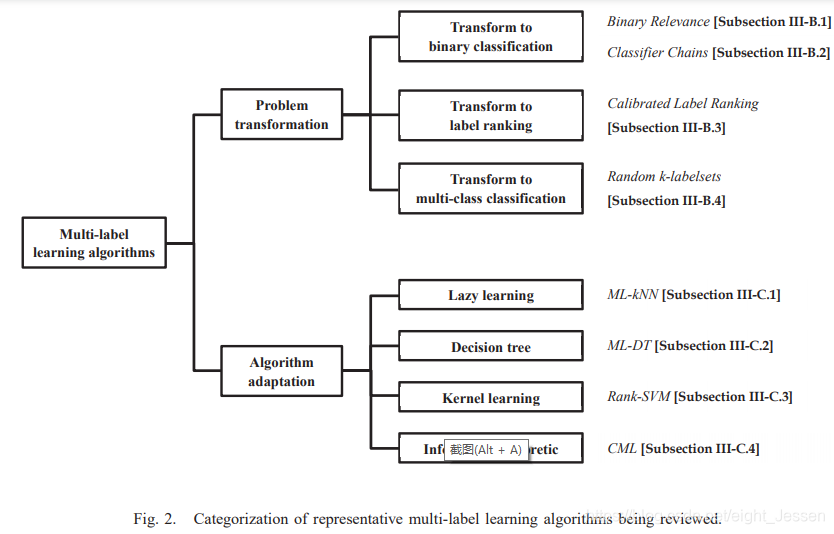
论文笔记:A review on multi-label learning
一、介绍 传统的监督学习是单标签学习,但是现实中一个实例可能对应多个标签。这篇文章介绍了多标签分类的定义和评价指标、多标签学习的算法还有其他相关的任务。 二、问题相关定义 2.1 多标签学习任务 假设 X R d X R^d XRd,表示d维的输入空间&am…...
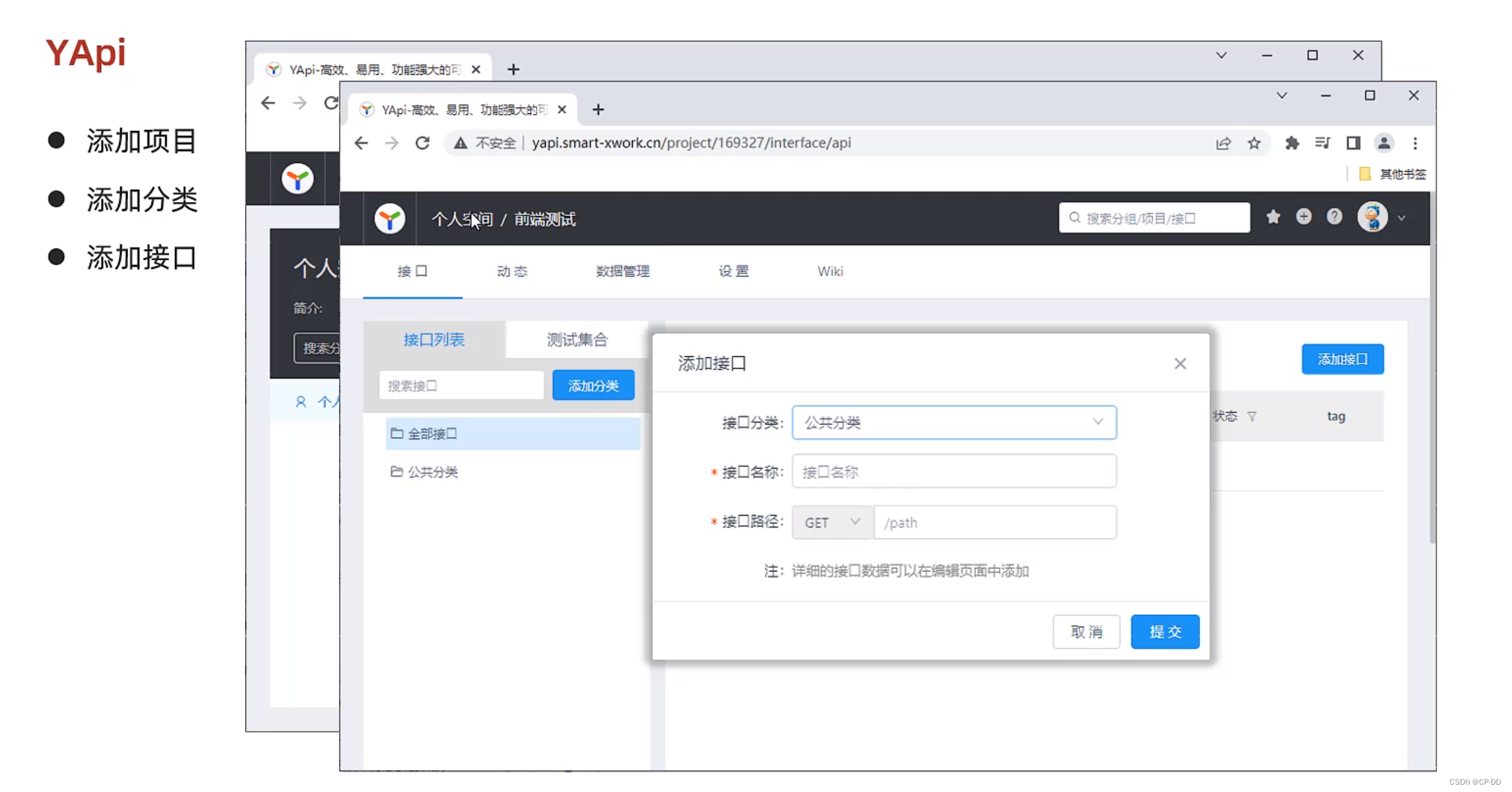
接口文档 YAPI介绍
YAPI介绍 YAPI使用流程...

LeetCode 300最长递增子序列 674最长连续递增序列 718最长重复子数组 | 代码随想录25期训练营day52
动态规划算法10 LeetCode 300 最长递增子序列 2023.12.15 题目链接代码随想录讲解[链接] int lengthOfLIS(vector<int>& nums) {//创建变量result存储最终答案,设默认值为1int result 1;//1确定dp数组,dp[i]表示以nums[i]为结尾的子数组的最长长度ve…...

Improving IP Geolocation with Target-Centric IP Graph (Student Abstract)
ABSTRACT 准确的IP地理定位对于位置感知的应用程序是必不可少的。虽然基于以路由器为中心(router-centric )的IP图的最新进展被认为是前沿的,但一个挑战仍然存在:稀疏IP图的流行(14.24%,少于10个节点,9.73%孤立)限制了图的学习。为了缓解这个问题,我们将目标主机(ta…...

华为技面三轮面试题
1. 最长回文子串 -- 中心扩散法 给你一个字符串 s,找到 s 中最长的回文子串。 如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。 示例 1: 输入:s "babad" 输出:"bab" 解释&…...
Linux arm架构下构建Electron安装包
上篇文章我们介绍 Electron 基本的运行开发与 windows 安装包构建简单流程,这篇文章我们从零到一构建 Linux arm 架构下安装包,实际上 Linux arm 的构建流程,同样适用于 Linux x86 环境,只不过需要各自的环境依赖,Linu…...
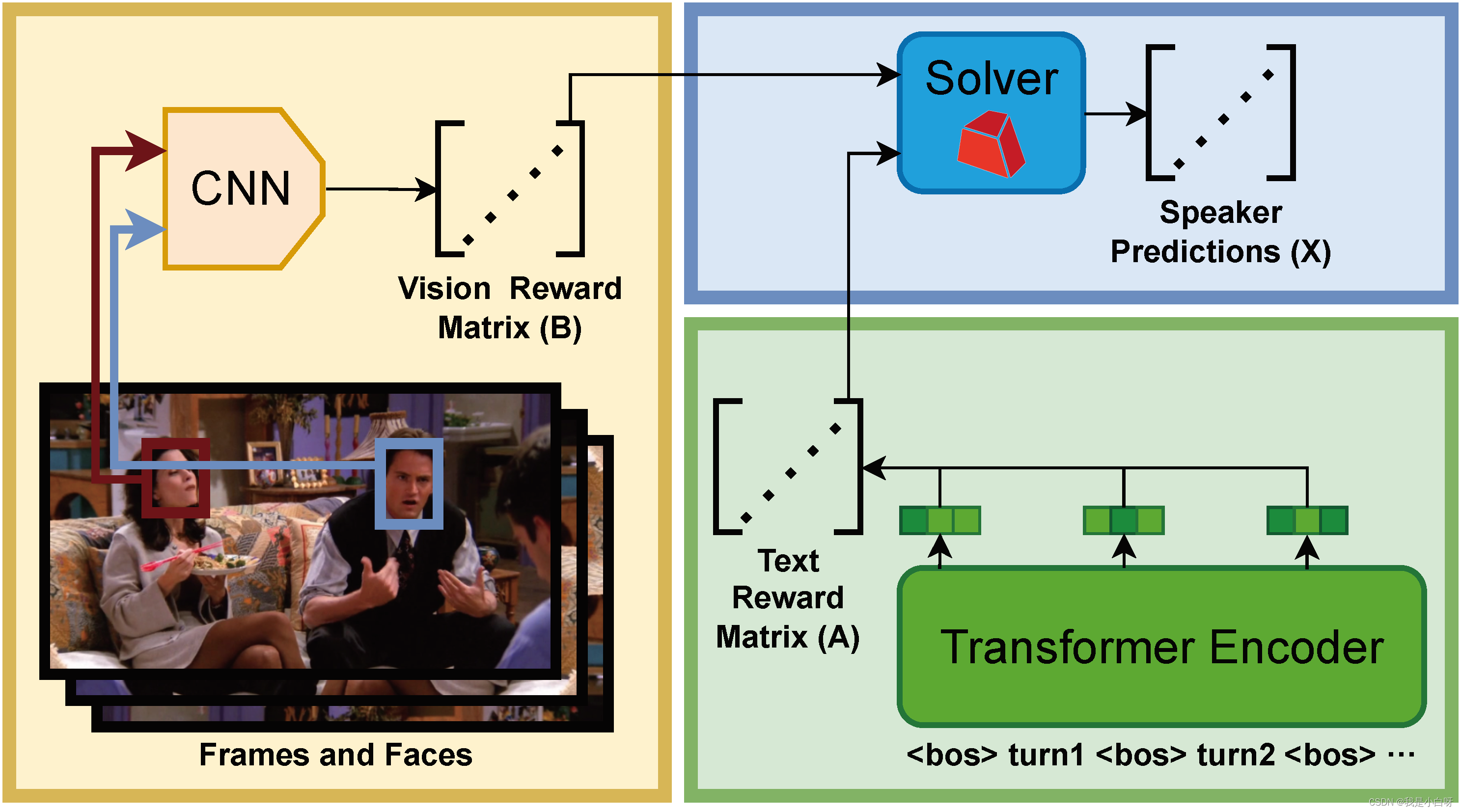
【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 NLP 部分
【CCF BDCI 2023】多模态多方对话场景下的发言人识别 Baseline 0.71 NLP 部分 概述NLP 简介文本处理词嵌入上下文理解 文本数据加载to_device 函数构造数据加载样本数量 len获取样本 getitem 分词构造函数调用函数轮次嵌入 RobertaRoberta 创新点NSP (Next Sentence Prediction…...

推免那些事
平生第一次搞推免,也是最后一次。错失了一些机会,也有幸获得了一些机会,值得祝庆,也值得反思。 以下记录为个人流水账。 个人背景 我的背景可以算不是非常好了,况且今年211受歧视比较严重。 学校:211&…...

华清远见嵌入式学习——QT——作业2
作业要求: 代码运行效果图: 登录失败 和 最小化 和 取消登录 登录成功 和 X号退出 代码: ①:头文件 #ifndef LOGIN_H #define LOGIN_H#include <QMainWindow> #include <QLineEdit> //行编辑器类 #include…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
