【数据挖掘 | 关联规则】FP-grow算法详解(附详细代码、案例实战、学习资源)
!

🤵♂️ 个人主页: @AI_magician
📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。
👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!🐱🏍
🙋♂️声明:本人目前大学就读于大二,研究兴趣方向人工智能&硬件(虽然硬件还没开始玩,但一直很感兴趣!希望大佬带带)

摘要: 本系列旨在普及那些深度学习路上必经的核心概念,文章内容都是博主用心学习收集所写,欢迎大家三联支持!本系列会一直更新,核心概念系列会一直更新!欢迎大家订阅
该文章收录专栏
[✨— 《深入解析机器学习:从原理到应用的全面指南》 —✨]
@toc
FP-Growth算法
Apriori算法需要多次扫描数据,I/O是很大的瓶颈。为了解决这个问题,FP-Growth(Frequent Pattern Growth)通过构建FP树(Frequent Pattern Tree)来避免生成候选项集,从而减少了搜索空间,提高了算法的效率。无论多少数据,只需要扫描两次数据集,因此提高了算法运行的效率。
FP Tree算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分,如下图所示:

1. 项头表(线性结构):里面记录了所有的1项频繁集出现的次数,按照次数降序排列。比如上图中B在所有10组数据中出现了8次,因此排在第一位。
- FP Tree(树结构):它将我们的原始数据集映射到了内存中的一颗FP树。
- 节点链表:所有项头表里的1项频繁集都是一个节点链表的头,它依次指向FP树中该1项频繁集出现的位置。这样做主要是方便项头表和FP Tree之间的联系,以查找和更新。
算法步骤:
-
构建项头表(Header Table):遍历数据集,统计每个项的支持度,删除支持度低于阈值的项,最后按照支持度降序排序。构建一个项头表,每个项头表项包含项的名称、支持度计数和指向该项在FP树中第一个节点的指针。在实际操作中需要扫描两次数据,第一次用于统计项支持度操作,第二次扫描用于删除支持度低于阈值中事务的项。(其中之所排序是因为在FP树的建立时,可以尽可能的共用祖先节点)
-
构建FP树:遍历数据集,读取每一条事务依次构建FP树。对于每个事务中的项,从根节点开始,如果该项在当前节点的子节点中存在,则增加子节点的支持度计数;否则,创建一个新的子节点,并更新项头表中该项的链表。最后构建得到的树称为FP树。
-
构建条件模式基:对于每个项头表中的项,从项头表链表的末尾开始,递归遍历该项的链表,生成以该项为后缀路径的条件模式基。每个条件模式基包含路径中除了当前项的其他项以及对应的支持度计数。
D的条件模式基如下图。将所有的祖先节点计数设置为叶子节点的计数,即变成{A:2, C:2,E:1 G:1,D:1, D:1},此时E节点和G节点由于在条件模式基里面的支持度低于阈值,被我们删除,最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2, C:2}。
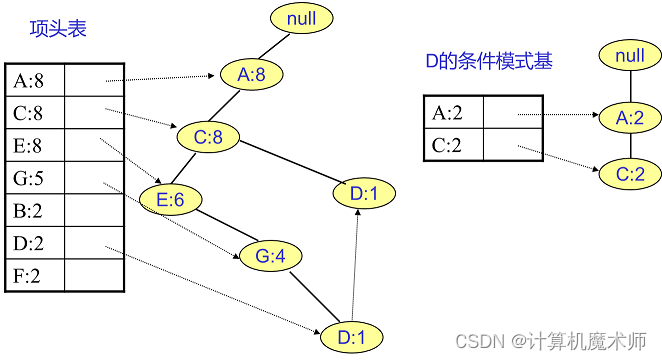
-
递归挖掘FP树:对于每个项头表中的项,将它与条件模式基组合,形成新的频繁项集。如果条件模式基非空,则以条件模式基为输入递归调用FP树构建和挖掘过程。
在上一步得到条件模式基后,结合得到 D的频繁2项集为{A:2,D:2}, {C:2,D:2}。递归合并二项集,得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集。
FP Tree算法改进了Apriori算法的I/O瓶颈,巧妙的利用了树结构,参考BIRCH聚类,BIRCH聚类也是巧妙的利用了树结构来提高算法运行速度。利用内存数据结构以空间换时间是常用的提高算法运行时间瓶颈的办法。
在实践中,FP Tree算法是可以用于生产环境的关联算法,而Apriori算法则做为先驱,起着关联算法指明灯的作用。除了FP Tree,像GSP,CBA之类的算法都是Apriori派系的。
经典案例和代码实现:
以下是一个使用Python的mlxtend库实现FP-Growth算法的示例代码:
from mlxtend.frequent_patterns import fpgrowth
from mlxtend.preprocessing import TransactionEncoder
import pandas as pd# 创建示例数据集
dataset = [['Milk', 'Eggs', 'Bread'],['Milk', 'Butter'],['Cheese', 'Bread', 'Butter'],['Milk', 'Eggs', 'Bread', 'Butter'],['Cheese', 'Bread', 'Butter']]# 使用TransactionEncoder将数据集转换为布尔矩阵
te = TransactionEncoder()
te_ary = te.fit(dataset).transform(dataset)
df = pd.DataFrame(te_ary, columns=te.columns_)# 使用fpgrowth函数查找频繁项集
frequent_itemsets = fpgrowth(df, min_support=0.2, use_colnames=True)print(frequent_itemsets)
这里使用了mlxtend库中的fpgrowth函数来执行FP-Growth算法。首先,将事务数据集转换为布尔矩阵表示,然后调用fpgrowth函数来寻找指定最小支持度阈值的频繁项集。
另外,如果你想使用自己实现的FP-Growth算法,可以参考相关的开源实现和算法细节。以下是一些学习资源,可以帮助你更深入地了解FP-Growth算法:
- Han, J., Pei, J., & Yin, Y. (2000). Mining frequent patterns without candidate generation. In Proceedings of the 2000 ACM SIGMOD international conference on Management of data (pp. 1-12).
- Agrawal, R., Imieliński, T., & Swami, A. (1993). Mining association rules between sets of items in large databases. ACM SIGMOD Record, 22(2), 207-216.
- mlxtend documentation: https://rasbt.github.io/mlxtend/
- Python implementation of FP-Growth algorithm: https://github.com/evandempsey/fp-growth
参考文章:
https://www.cnblogs.com/pinard/p/6307064.html

🤞到这里,如果还有什么疑问🤞🎩欢迎私信博主问题哦,博主会尽自己能力为你解答疑惑的!🎩🥳如果对你有帮助,你的赞是对博主最大的支持!!🥳
相关文章:

【数据挖掘 | 关联规则】FP-grow算法详解(附详细代码、案例实战、学习资源)
! 🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&a…...
 11)
力扣题目学习笔记(OC + Swift) 11
11.盛最多水的容器 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 返回容器可以储存的最大水量。 说明:你不能倾…...
JVM基础入门
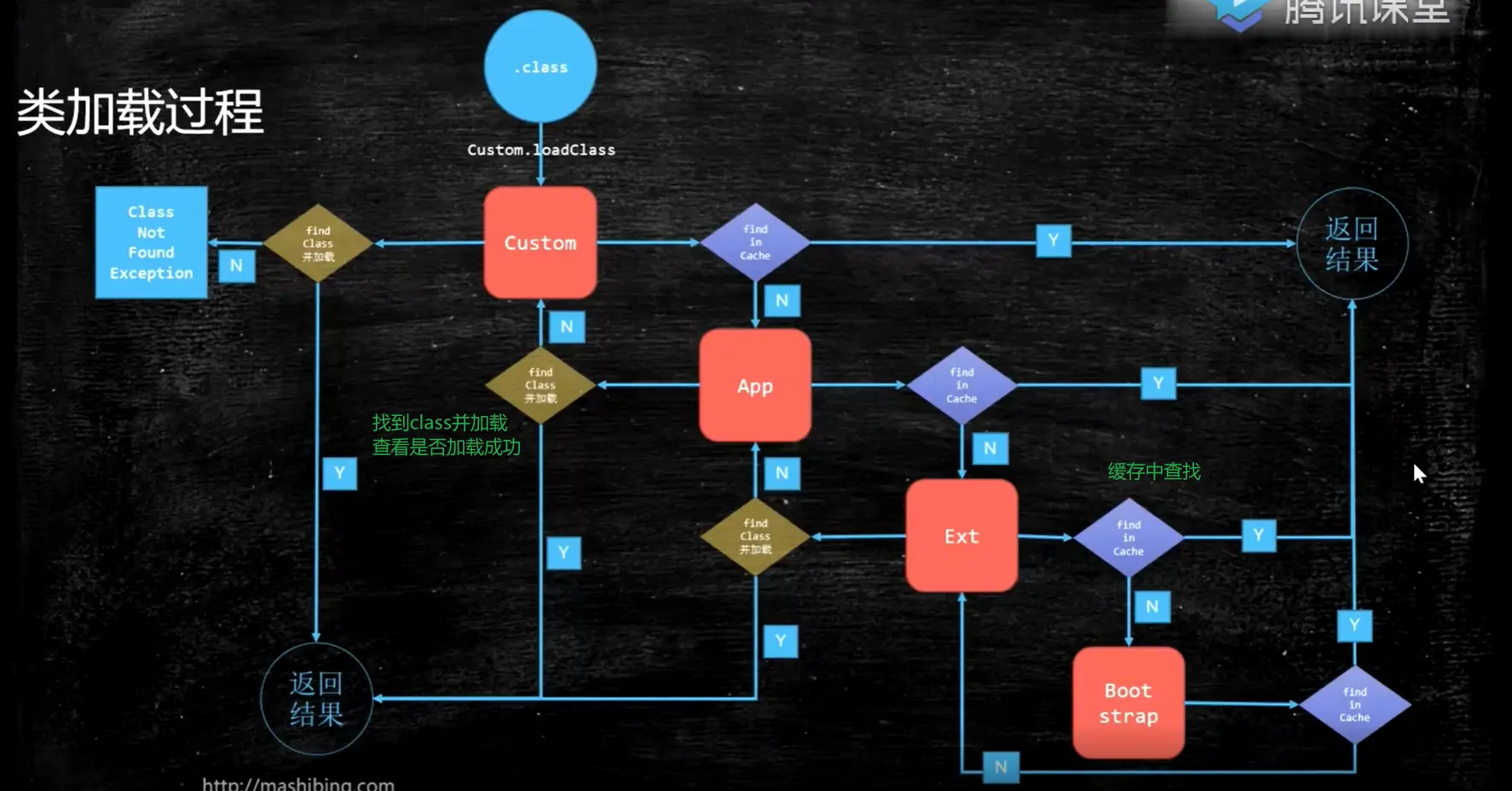
JVM 基础入门 JVM 基础 聊一聊 Java 从编码到执行到底是一个怎么样的过程? 假设我们有一个文件 x.Java,你执行 javac,它就会变成 x.class。 这个 class 怎么执行的? 当我们调用 Java 命令的时候,class 会被 load 到…...

前端真的死了吗
随着人工智能和低代码的崛起,“前端已死”的声音逐渐兴起。前端已死?尊嘟假嘟?快来发表你的看法吧! 以下方向仅供参考。 一、为什么会出现“前端已死”的言论 前端已死这个言论 是出自于2022年开始 ,2022年下半年疫情…...

前后端分离开发
前期 前后端混合开发 后期 前后端分离开发...
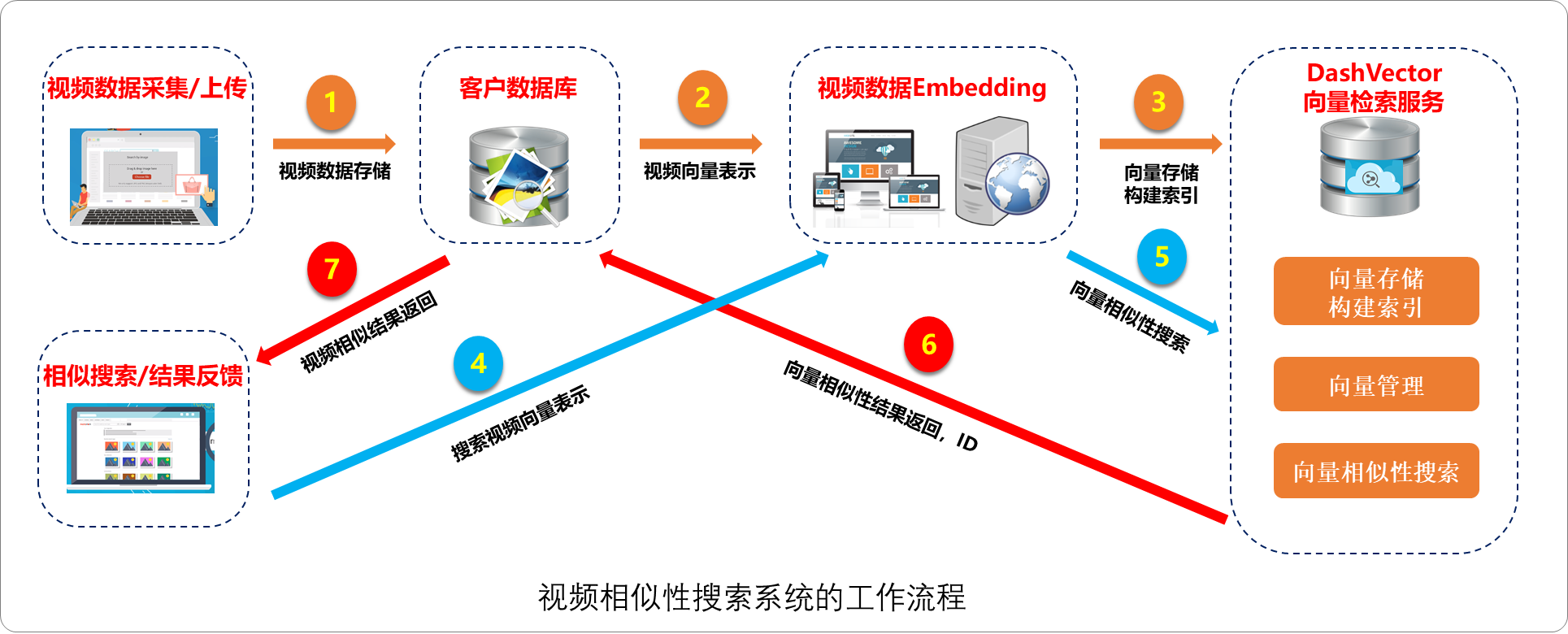
向量数据库——AI时代的基座
向量数据库——AI时代的基座 1.前言 向量数据库在构建基于大语言模型的行业智能应用中扮演着重要角色。大模型虽然能回答一般性问题,但在垂直领域服务中,其知识深度、准确度和时效性有限。为了解决这一问题,企业可以利用向量数据库结合大模…...

【️什么是分布式系统的一致性 ?】
😊引言 🎖️本篇博文约8000字,阅读大约30分钟,亲爱的读者,如果本博文对您有帮助,欢迎点赞关注!😊😊😊 🖥️什么是分布式系统的一致性 ?…...

鸿蒙ArkTS Web组件加载空白的问题原因及解决方案
问题症状 初学鸿蒙开发,按照官方文档Web组件文档《使用Web组件加载页面》示例中的代码照抄运行后显示空白,纠结之余多方搜索后扔无解决方法。 运行代码 import web_webview from ohos.web.webviewEntry Component struct Index {controller: web_webv…...
【Java】网络编程-UDP回响服务器客户端简单代码编写
这一篇文章我们将讲述网络编程中UDP服务器客户端的编程代码 1、前置知识 UDP协议全称是用户数据报协议,在网络中它与TCP协议一样用于处理数据包,是一种无连接的协议。 UDP的特点有:无连接、尽最大努力交付、面向报文、没有拥塞控制 本文讲…...

【设计模式】之工厂模式
工厂模式 1.介绍 工厂模式(创建型模式),是我们最常用的实例化对象模式,是用工厂方法代替new操作的一种模式;在工厂模式中,我们在创建对象时不会对客户端暴露创建逻辑,并且是通过使用一个共同的…...

70.爬楼梯
题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 注意: 给定 n 是一个正整数。 示例 1: 输入: 2 输出: 2 解释: 有两种方法可以爬到楼顶…...

【论文解读】ICLR 2024高分作:ViT需要寄存器
来源:投稿 作者:橡皮 编辑:学姐 论文链接:https://arxiv.org/abs/2309.16588 摘要: Transformer最近已成为学习视觉表示的强大工具。在本文中,我们识别并表征监督和自监督 ViT 网络的特征图中的伪影。这些…...
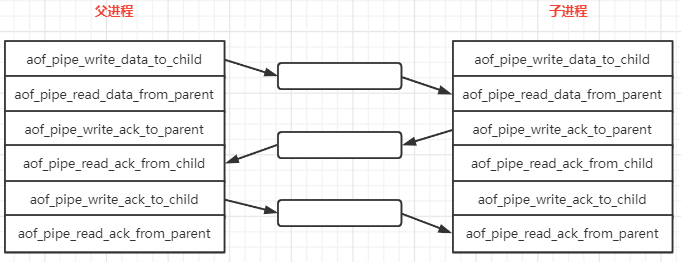
【Redis】AOF 基础
因为 Redis AOF 的实现有些绕, 就分成 2 篇进行分析, 本篇主要是介绍一下 AOF 的一些特性和依赖的其他函数的逻辑,为下一篇 (Redis AOF 源码) 源码分析做一些铺垫。 AOF 全称: Append Only File, 是 Redis 提供了一种数据保存模式, Redis 默认不开启。 AOF 采用日志的形式来记…...
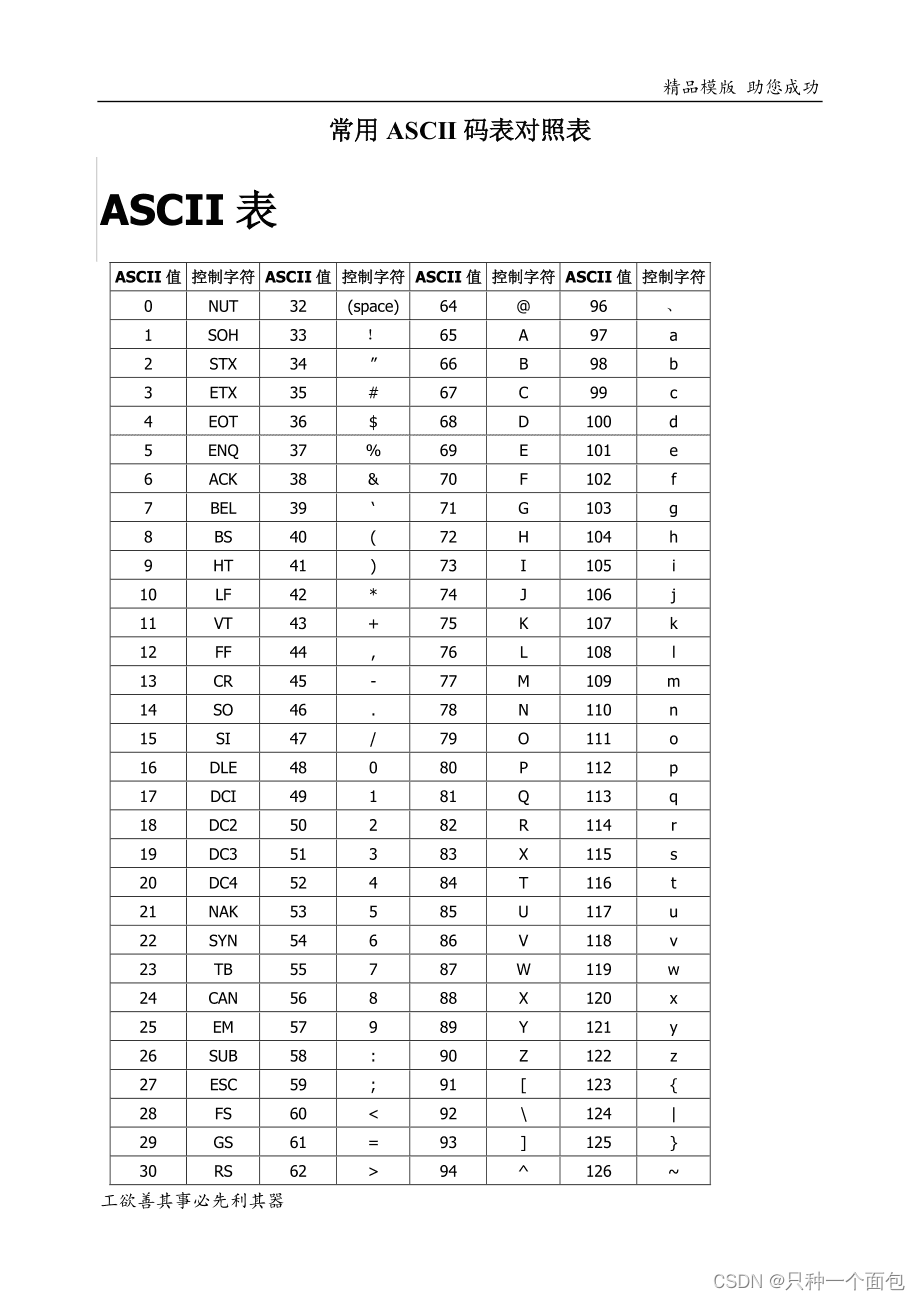
C语言—每日选择题—Day50
一天一天的更新,也是达到50天了,精选的题有250道,博主累计做了不下500道选择题,最喜欢的题型就是指针和数组之间的计算呀,不知道关注我的小伙伴是不是一直在坚持呢?文末有投票,大家可以投票让博…...
[C/C++]——内存管理
学习C/C的内存管理 前言:一、C/C的内存分布二、C语言中动态内存管理方式三、C中动态内存管理方式3.1、new/delete操作符3.1.2、new/delete操作内置类型3.1.3、new/delete操作自定义类型 3.2、认识operator new和operator delete函数3.3、了解new和delete的实现原理3…...
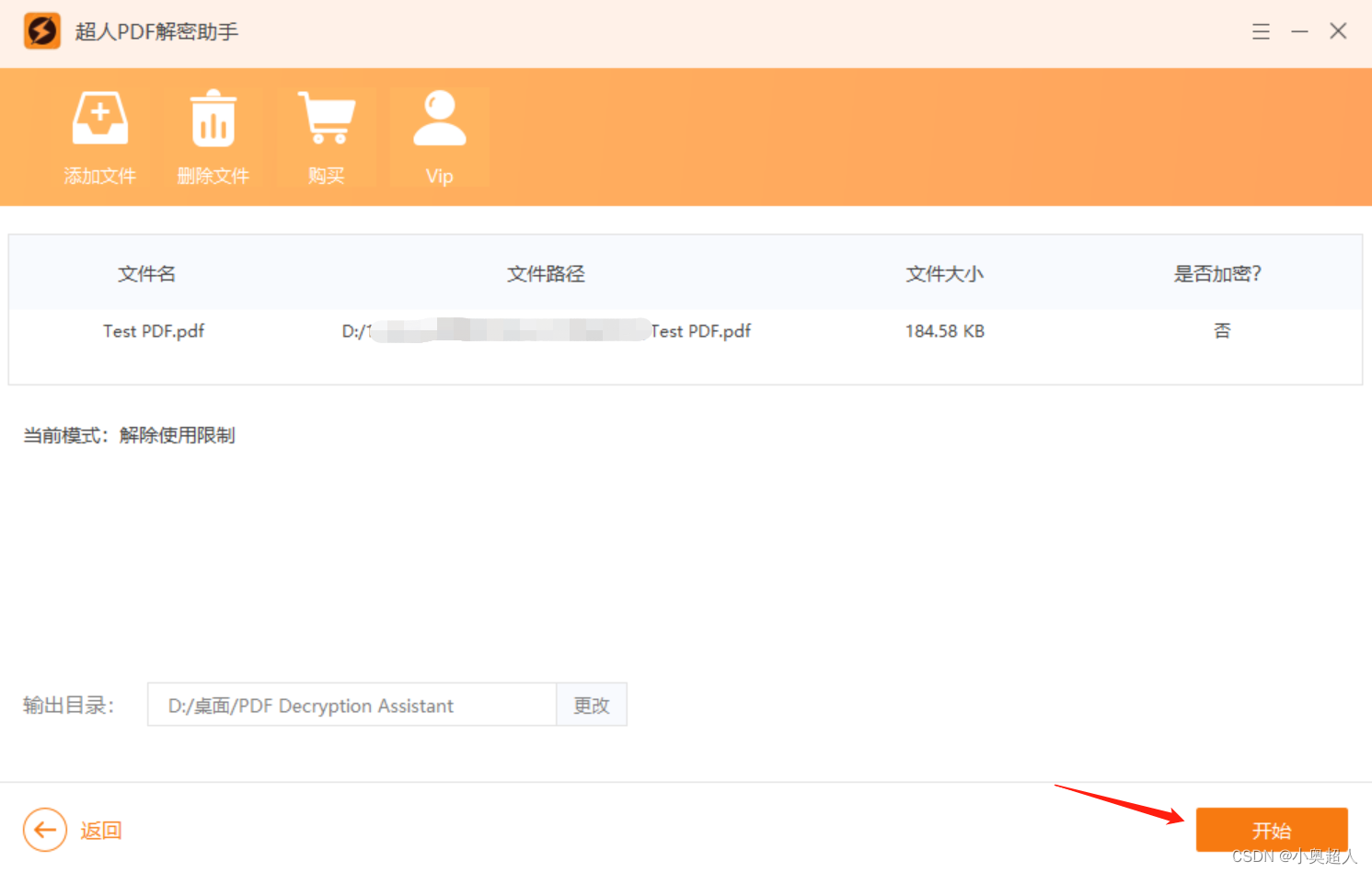
PDF文件的限制编辑,如何设置?
想要给PDF文件设置一个密码防止他人对文件进行编辑,那么我们可以对PDF文件设置限制编辑,设置方法很简单,我们在PDF编辑器中点击文件 – 属性 – 安全,在权限下拉框中选中【密码保护】 然后在密码保护界面中,我们勾选【…...
Linux 中使用 docker 安装 Elasticsearch 及 Kibana
Linux 中使用 docker 安装 Elasticsearch 及 Kibana 安装 Elasticsearch 和 Kibana安装分词插件 ik_smart 安装 Elasticsearch 和 Kibana 查看当前运行的镜像及本地已经下载的镜像,确认之前没有安装过 ES 和 Kibana 镜像 docker ps docker images从远程镜像仓库拉…...

在Flutter中使用PhotoViewGallery指南
介绍 Flutter中的PhotoViewGallery是一个功能强大的插件,用于在应用中展示可缩放的图片。无论是构建图像浏览器、相册应用,还是需要在应用中查看大图的场景,PhotoViewGallery都是一个不错的选择。 添加依赖 首先,需要在pubspec…...

c语言中的static静态(1)static修饰局部变量
#include<stdio.h> void test() {static int i 1;i;printf("%d ", i); } int main() {int j 0;while (j < 5){test();j j 1;}return 0; } 在上面的代码中,static修饰局部变量。 当用static定义一个局部变量后,这时局部变量就是…...

生信算法4 - 获取overlap序列索引和序列的算法
生信序列基本操作算法 建议在Jupyter实践,python版本3.9 1. 获取overlap序列索引和序列的算法实现 # min_length 最小overlap碱基数量3个 def getOverlapIndexAndSequence(a, b, min_length3):""" Return length of longest suffix of a matching…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的,如果需要进行.NET开发,则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET,所以要进…...
