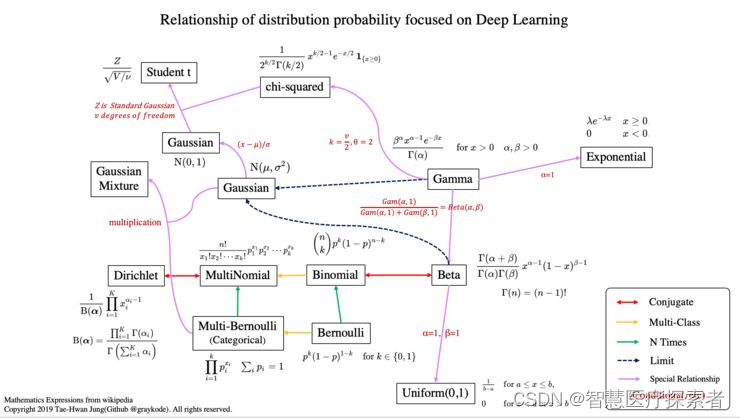
深度学习中的13种概率分布
1 概率分布概述
-
共轭意味着它有共轭分布的关系。
在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。
-
多分类表示随机方差大于 2。
-
n 次意味着我们也考虑了先验概率 p(x)。
2 分布概率与特征
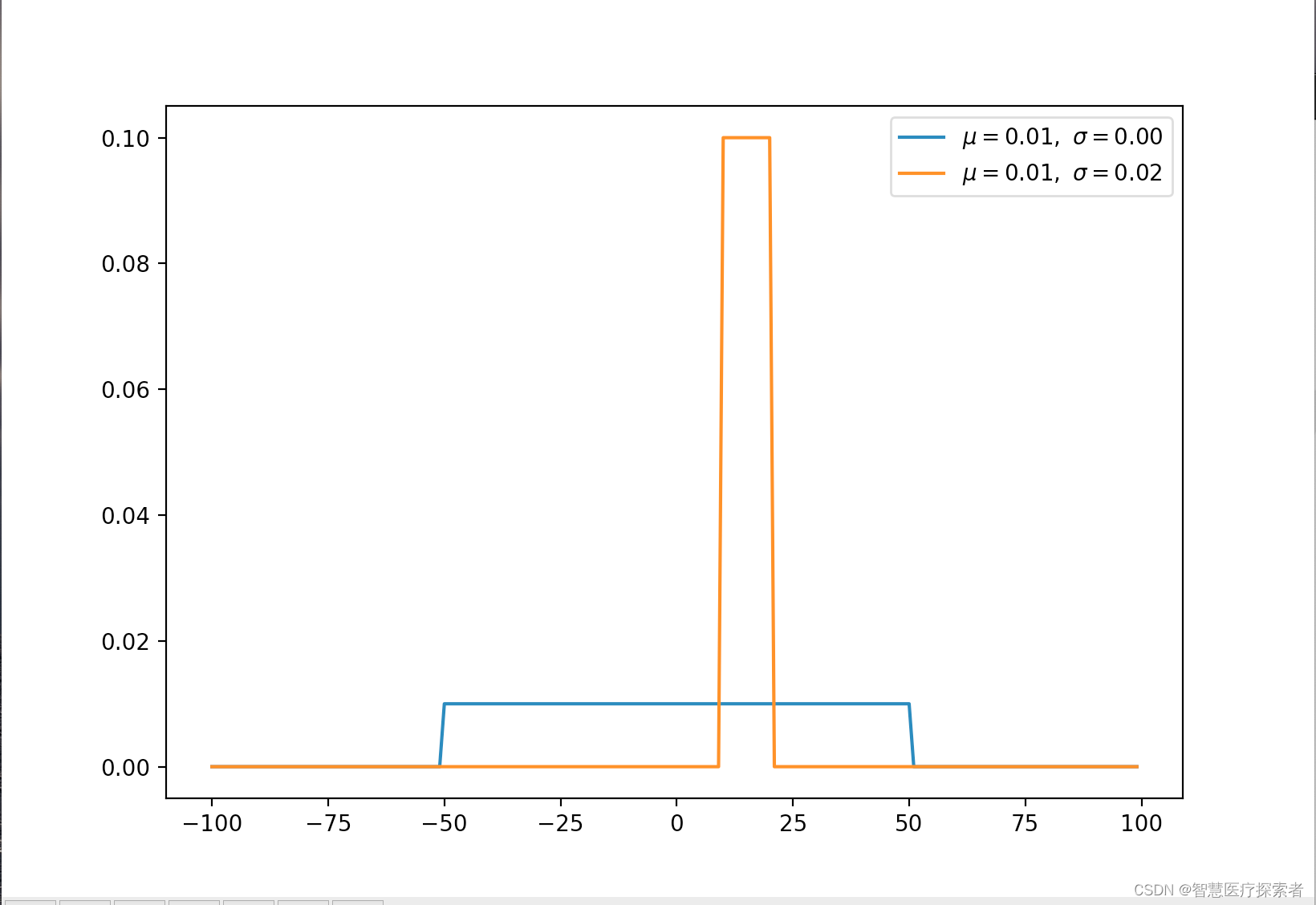
2.1 均匀分布(连续)
均匀分布在 [a,b] 上具有相同的概率值,是简单概率分布。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef uniform(x, a, b):y = [1 / (b - a) if a <= val and val <= belse 0 for val in x]return x, y, np.mean(y), np.std(y)x = np.arange(-100, 100) # define range of x
for ls in [(-50, 50), (10, 20)]:a, b = ls[0], ls[1]x, y, u, s = uniform(x, a, b)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))plt.legend()
plt.show()运行代码显示:
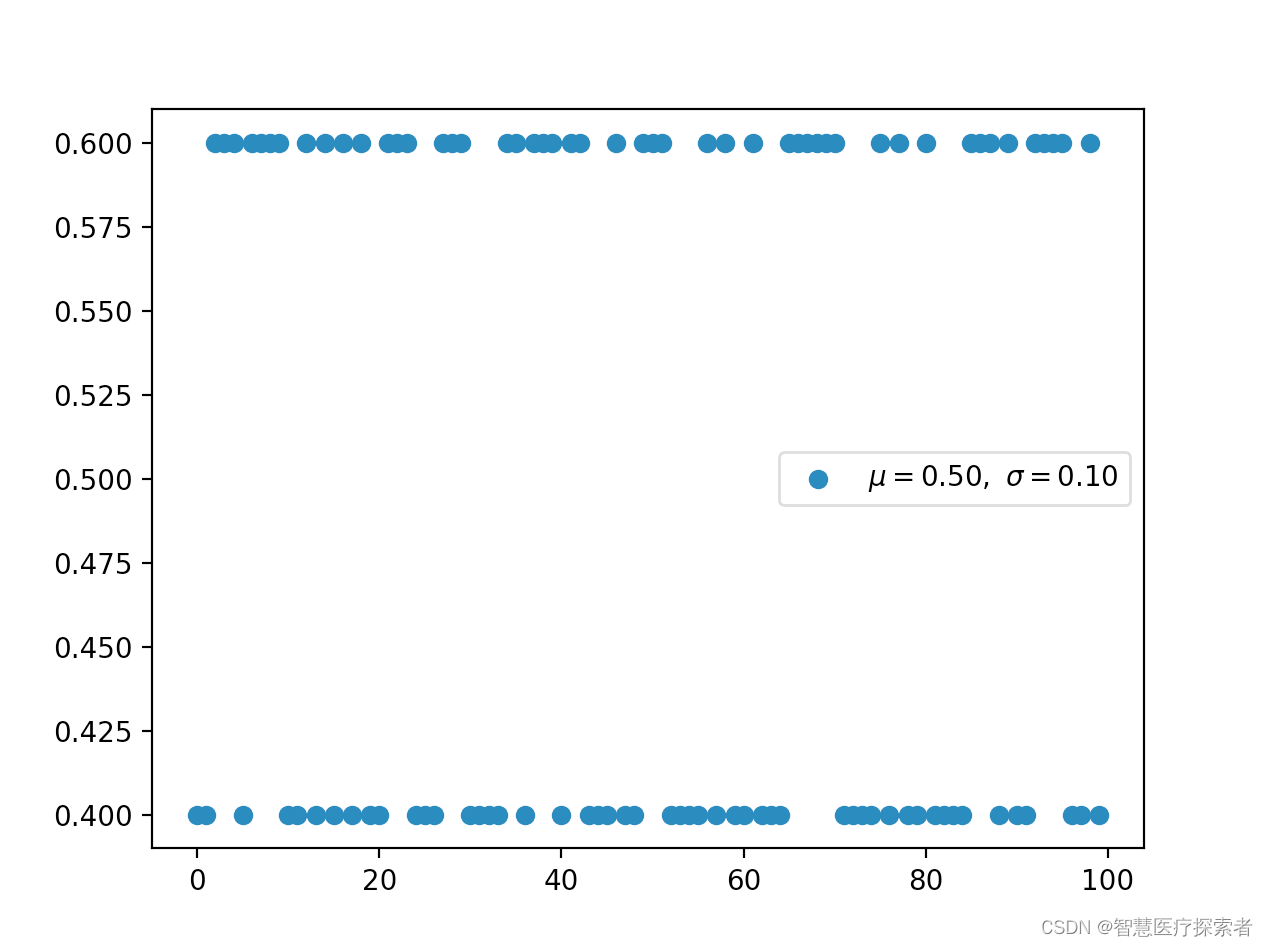
2.2 伯努利分布(离散)
-
先验概率 p(x)不考虑伯努利分布。因此,如果我们对最大似然进行优化,那么我们很容易被过度拟合。
-
利用二元交叉熵对二项分类进行分类。它的形式与伯努利分布的负对数相同。
示例代码:
import random
import numpy as np
from matplotlib import pyplot as pltdef bernoulli(p, k):return p if k else 1 - pn_experiment = 100
p = 0.6
x = np.arange(n_experiment)
y = []
for _ in range(n_experiment):pick = bernoulli(p, k=bool(random.getrandbits(1)))y.append(pick)u, s = np.mean(y), np.std(y)
plt.scatter(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:
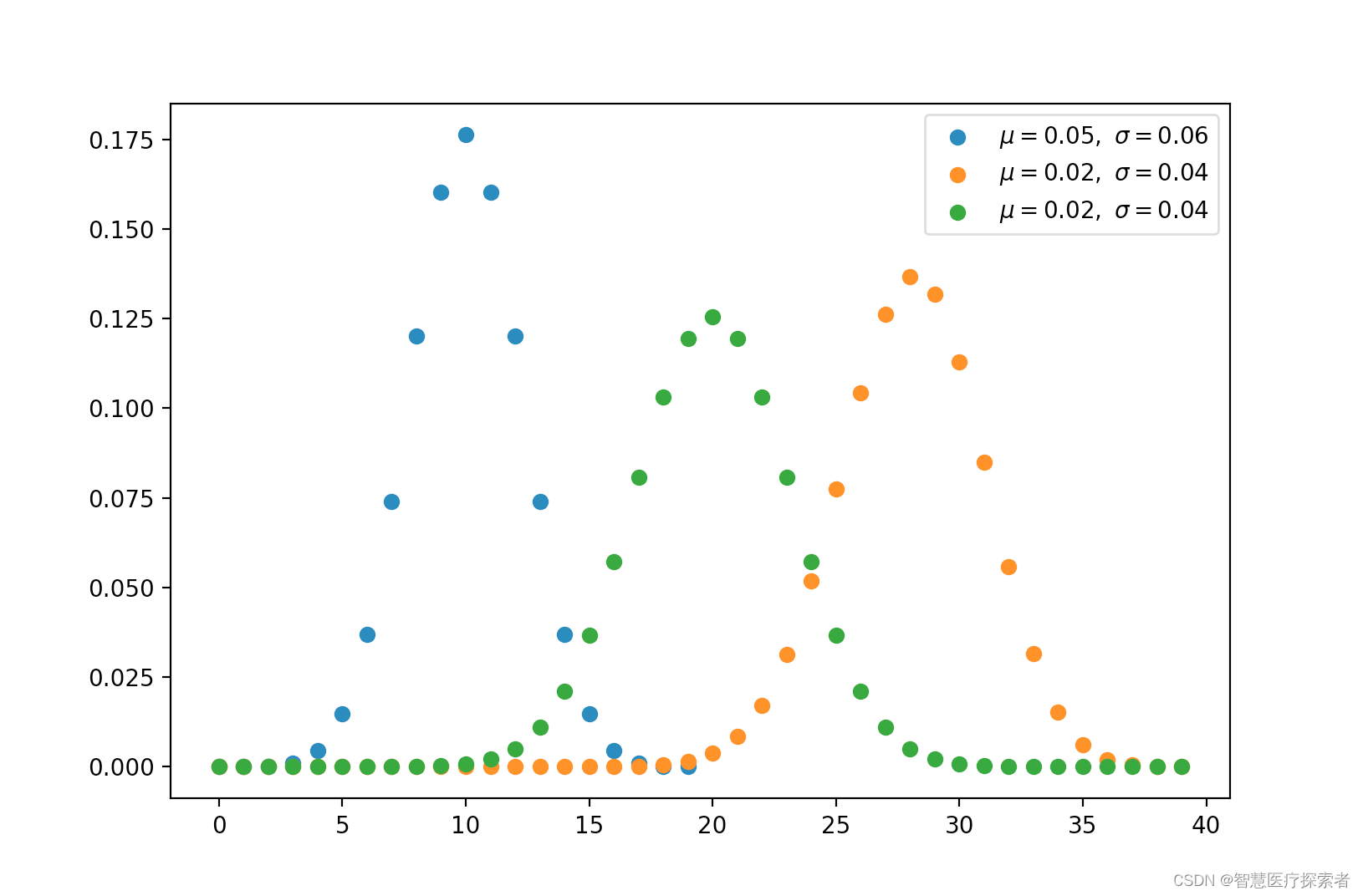
2.3 二项分布(离散)
-
参数为 n 和 p 的二项分布是一系列 n 个独立实验中成功次数的离散概率分布。
-
二项式分布是指通过指定要提前挑选的数量而考虑先验概率的分布。
示例代码:
import numpy as np
from matplotlib import pyplot as pltimport operator as op
from functools import reducedef const(n, r):r = min(r, n-r)numer = reduce(op.mul, range(n, n-r, -1), 1)denom = reduce(op.mul, range(1, r+1), 1)return numer / denomdef binomial(n, p):q = 1 - py = [const(n, k) * (p ** k) * (q ** (n-k)) for k in range(n)]return y, np.mean(y), np.std(y)for ls in [(0.5, 20), (0.7, 40), (0.5, 40)]:p, n_experiment = ls[0], ls[1]x = np.arange(n_experiment)y, u, s = binomial(n_experiment, p)plt.scatter(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))plt.legend()
plt.show()运行代码显示:
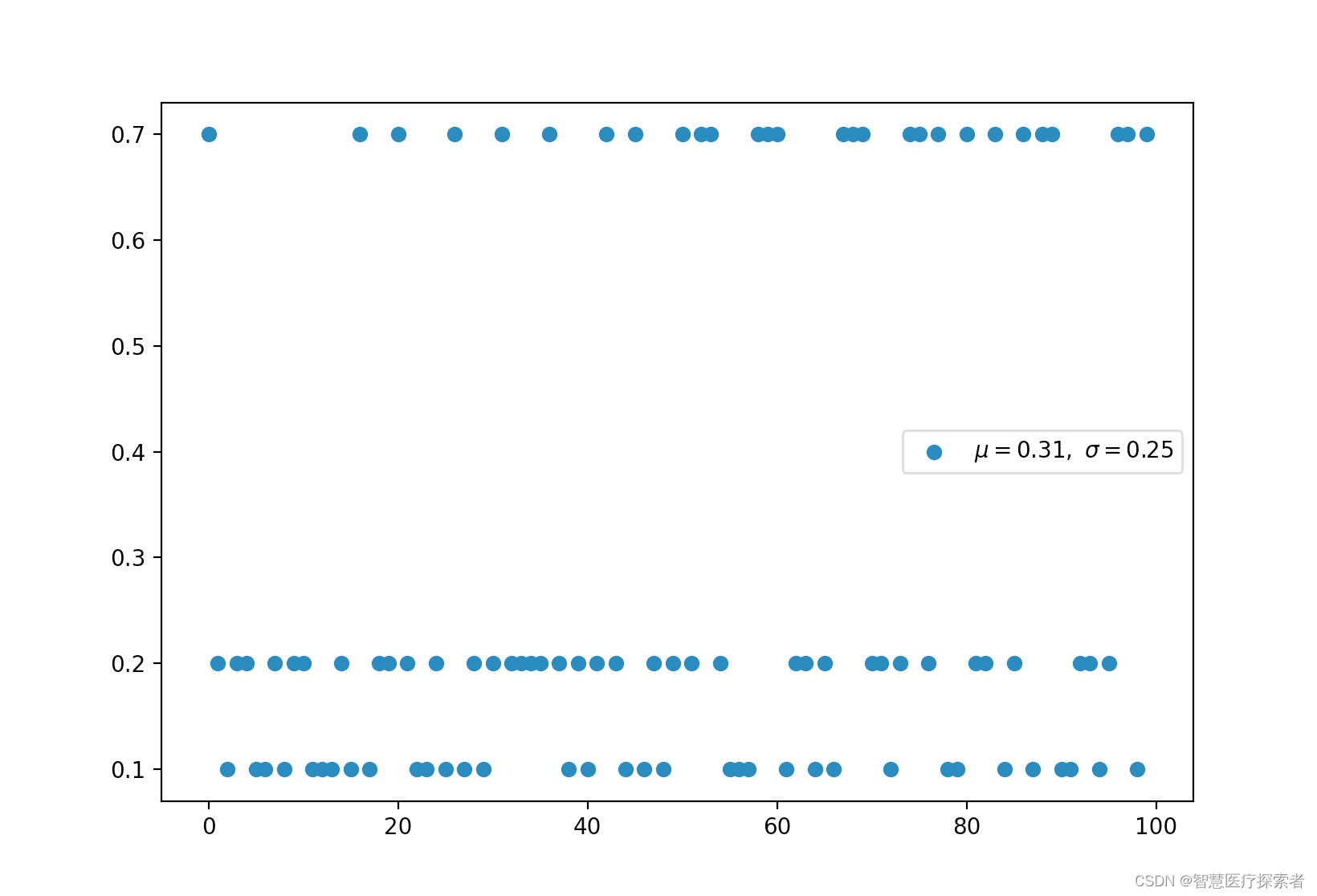
2.4 多伯努利分布,分类分布(离散)
-
多伯努利称为分类分布。
-
交叉熵和采取负对数的多伯努利分布具有相同的形式。
示例代码:
import random
import numpy as np
from matplotlib import pyplot as pltdef categorical(p, k):return p[k]n_experiment = 100
p = [0.2, 0.1, 0.7]
x = np.arange(n_experiment)
y = []
for _ in range(n_experiment):pick = categorical(p, k=random.randint(0, len(p) - 1))y.append(pick)u, s = np.mean(y), np.std(y)
plt.scatter(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:
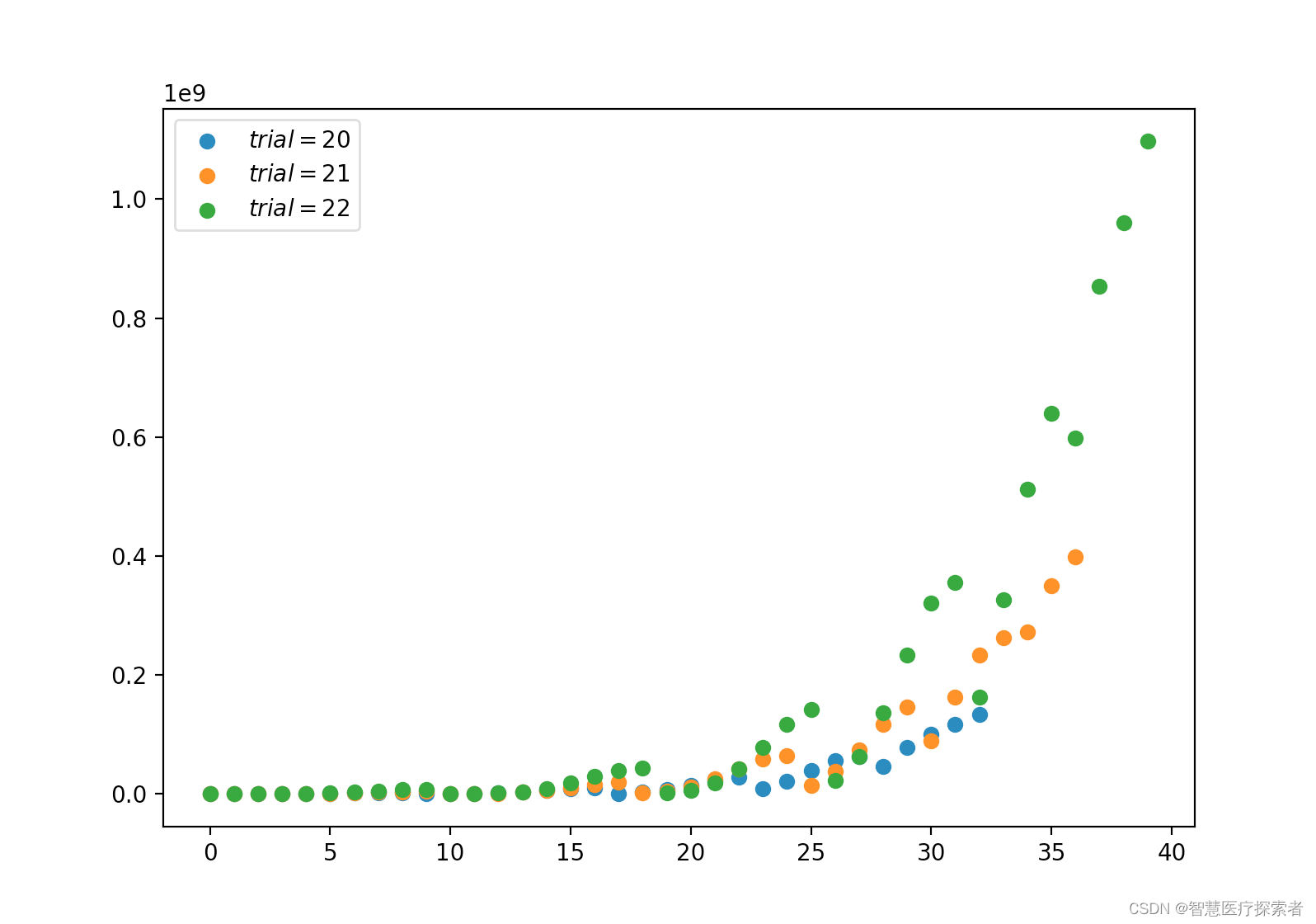
2.5 多项式分布(离散)
多项式分布与分类分布的关系与伯努尔分布与二项分布的关系相同。
示例代码:
import numpy as np
from matplotlib import pyplot as pltimport operator as op
from functools import reducedef factorial(n):return reduce(op.mul, range(1, n + 1), 1)def const(n, a, b, c):"""return n! / a! b! c!, where a+b+c == n"""assert a + b + c == nnumer = factorial(n)denom = factorial(a) * factorial(b) * factorial(c)return numer / denomdef multinomial(n):""":param x : list, sum(x) should be `n`:param n : number of trial:param p: list, sum(p) should be `1`"""# get all a,b,c where a+b+c == n, a<b<cls = []for i in range(1, n + 1):for j in range(i, n + 1):for k in range(j, n + 1):if i + j + k == n:ls.append([i, j, k])y = [const(n, l[0], l[1], l[2]) for l in ls]x = np.arange(len(y))return x, y, np.mean(y), np.std(y)for n_experiment in [20, 21, 22]:x, y, u, s = multinomial(n_experiment)plt.scatter(x, y, label=r'$trial=%d$' % (n_experiment))plt.legend()
plt.show()运行代码显示:
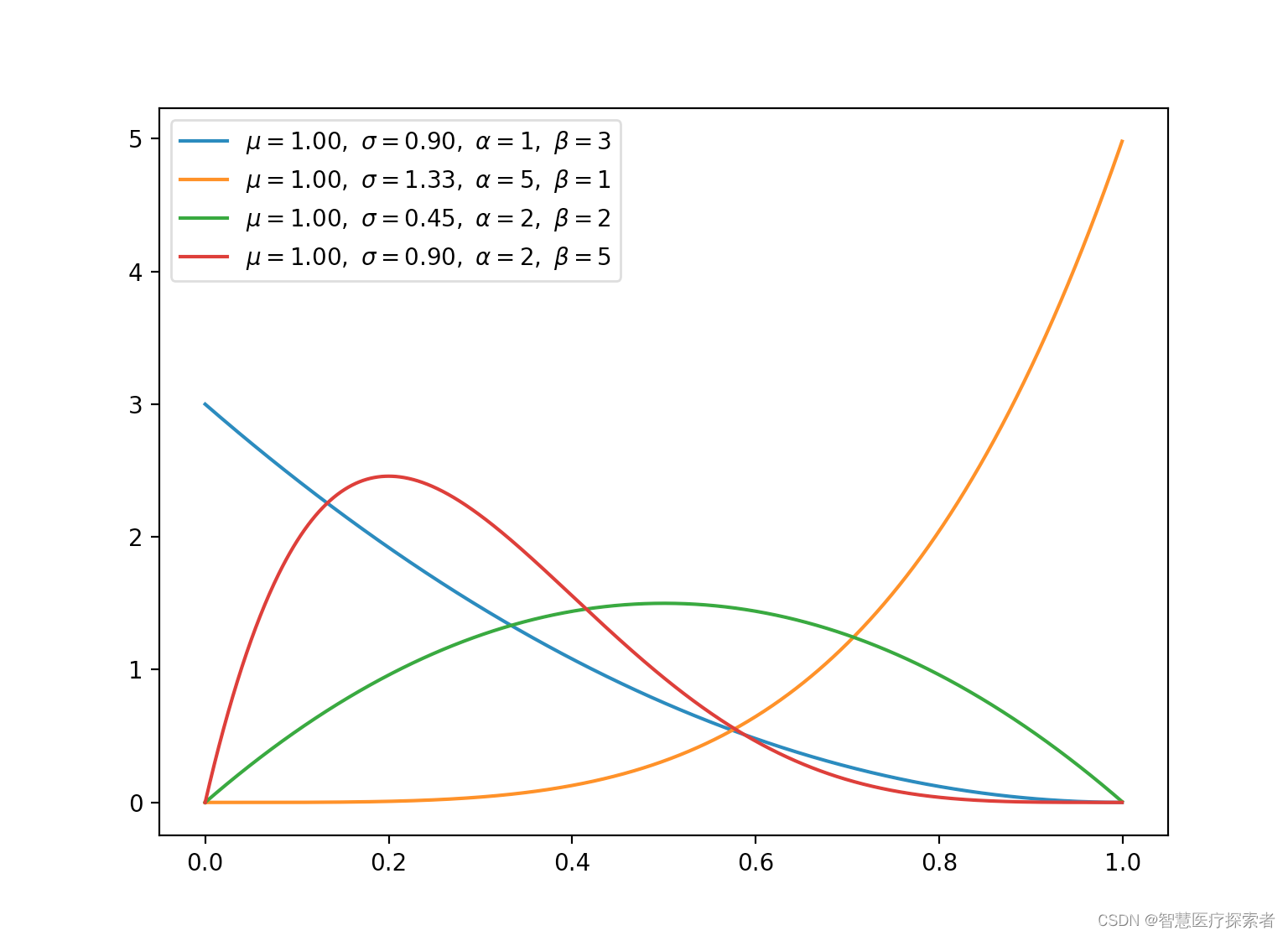
2.6 β分布(连续)
-
β分布与二项分布和伯努利分布共轭。
-
利用共轭,利用已知的先验分布可以更容易地得到后验分布。
-
当β分布满足特殊情况(α=1,β=1)时,均匀分布是相同的。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef beta(x, a, b):gamma = gamma_function(a + b) / \(gamma_function(a) * gamma_function(b))y = gamma * (x ** (a - 1)) * ((1 - x) ** (b - 1))return x, y, np.mean(y), np.std(y)for ls in [(1, 3), (5, 1), (2, 2), (2, 5)]:a, b = ls[0], ls[1]# x in [0, 1], trial is 1/0.001 = 1000x = np.arange(0, 1, 0.001, dtype=np.float)x, y, u, s = beta(x, a=a, b=b)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'r'\ \alpha=%d,\ \beta=%d$' % (u, s, a, b))
plt.legend()
plt.show()运行代码显示:
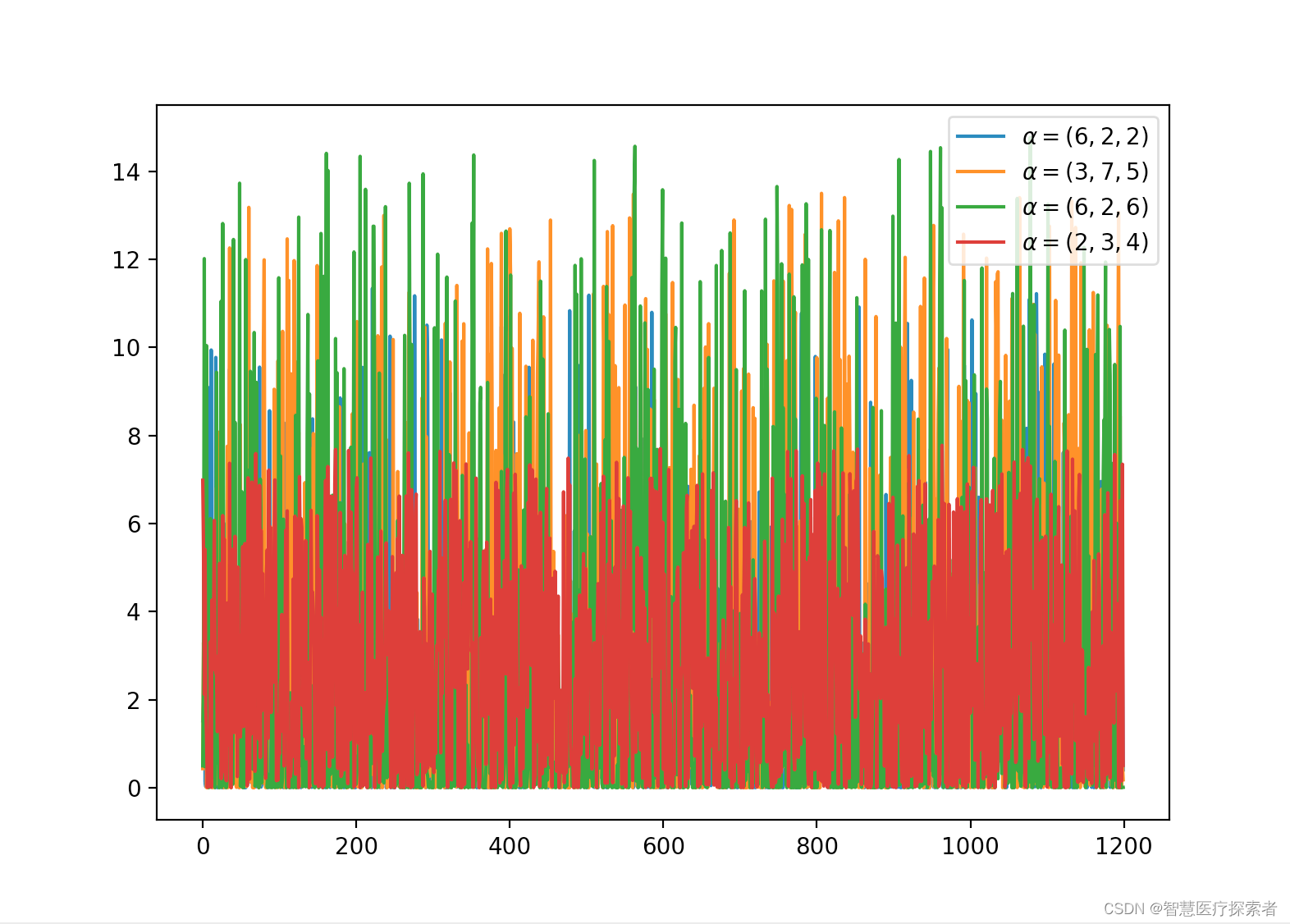
2.7 Dirichlet 分布(连续)
-
dirichlet 分布与多项式分布是共轭的。
-
如果 k=2,则为β分布。
示例代码:
from random import randint
import numpy as np
from matplotlib import pyplot as pltdef normalization(x, s):""":return: normalizated list, where sum(x) == s"""return [(i * s) / sum(x) for i in x]def sampling():return normalization([randint(1, 100),randint(1, 100), randint(1, 100)], s=1)def gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef beta_function(alpha):""":param alpha: list, len(alpha) is k:return:"""numerator = 1for a in alpha:numerator *= gamma_function(a)denominator = gamma_function(sum(alpha))return numerator / denominatordef dirichlet(x, a, n):""":param x: list of [x[1,...,K], x[1,...,K], ...], shape is (n_trial, K):param a: list of coefficient, a_i > 0:param n: number of trial:return:"""c = (1 / beta_function(a))y = [c * (xn[0] ** (a[0] - 1)) * (xn[1] ** (a[1] - 1))* (xn[2] ** (a[2] - 1)) for xn in x]x = np.arange(n)return x, y, np.mean(y), np.std(y)n_experiment = 1200
for ls in [(6, 2, 2), (3, 7, 5), (6, 2, 6), (2, 3, 4)]:alpha = list(ls)# random samping [x[1,...,K], x[1,...,K], ...], shape is (n_trial, K)# each sum of row should be one.x = [sampling() for _ in range(1, n_experiment + 1)]x, y, u, s = dirichlet(x, alpha, n=n_experiment)plt.plot(x, y, label=r'$\alpha=(%d,%d,%d)$' % (ls[0], ls[1], ls[2]))plt.legend()
plt.show()运行代码显示:
2.8 伽马分布(连续)
-
如果 gamma(a,1)/gamma(a,1)+gamma(b,1)与 beta(a,b)相同,则 gamma 分布为β分布。
-
指数分布和卡方分布是伽马分布的特例。
代码示例:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef gamma(x, a, b):c = (b ** a) / gamma_function(a)y = c * (x ** (a - 1)) * np.exp(-b * x)return x, y, np.mean(y), np.std(y)for ls in [(1, 1), (2, 1), (3, 1), (2, 2)]:a, b = ls[0], ls[1]x = np.arange(0, 20, 0.01, dtype=np.float)x, y, u, s = gamma(x, a=a, b=b)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'r'\ \alpha=%d,\ \beta=%d$' % (u, s, a, b))
plt.legend()
plt.show()运行代码显示:
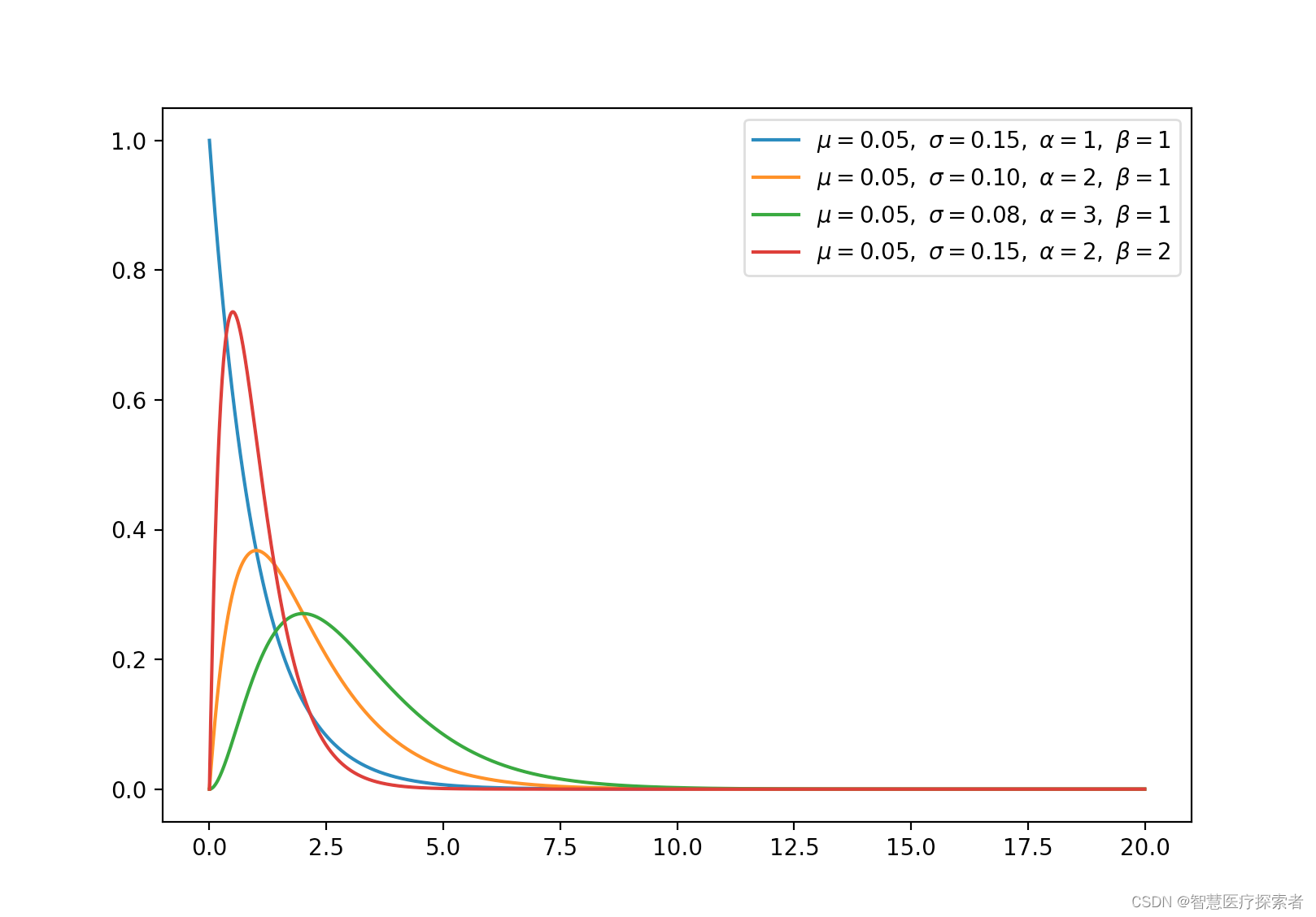
2.9 指数分布(连续)
指数分布是 α 为 1 时 γ 分布的特例。
import numpy as np
from matplotlib import pyplot as pltdef exponential(x, lamb):y = lamb * np.exp(-lamb * x)return x, y, np.mean(y), np.std(y)for lamb in [0.5, 1, 1.5]:x = np.arange(0, 20, 0.01, dtype=np.float)x, y, u, s = exponential(x, lamb=lamb)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f,'r'\ \lambda=%d$' % (u, s, lamb))
plt.legend()
plt.show()运行代码显示
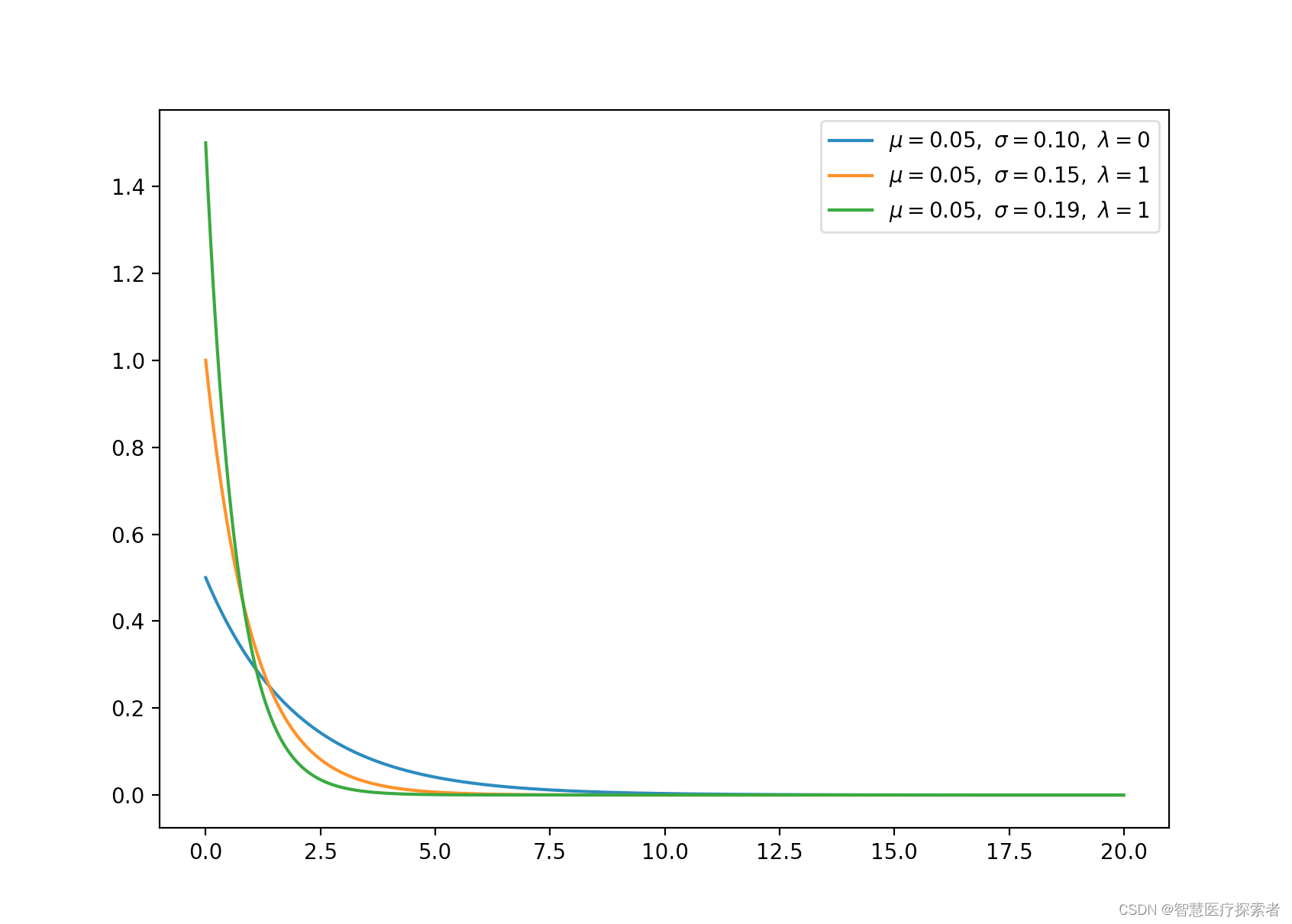
2.10 高斯分布(连续)
高斯分布是一种非常常见的连续概率分布。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gaussian(x, n):u = x.mean()s = x.std()# divide [x.min(), x.max()] by nx = np.linspace(x.min(), x.max(), n)a = ((x - u) ** 2) / (2 * (s ** 2))y = 1 / (s * np.sqrt(2 * np.pi)) * np.exp(-a)return x, y, x.mean(), x.std()x = np.arange(-100, 100) # define range of x
x, y, u, s = gaussian(x, 10000)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:

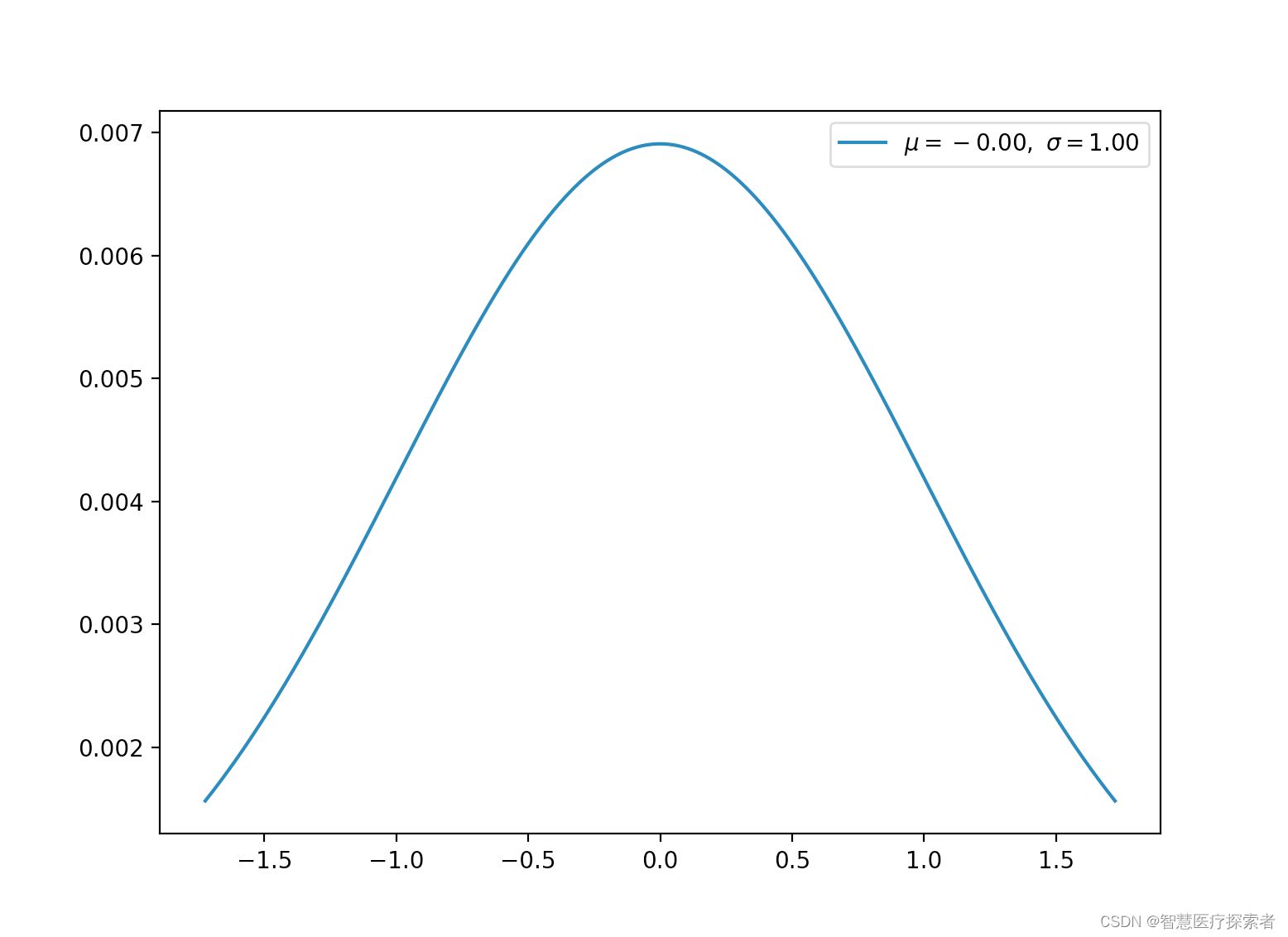
2.11 标准正态分布(连续)
标准正态分布为特殊的高斯分布,平均值为 0,标准差为 1。
import numpy as np
from matplotlib import pyplot as pltdef normal(x, n):u = x.mean()s = x.std()# normalizationx = (x - u) / s# divide [x.min(), x.max()] by nx = np.linspace(x.min(), x.max(), n)a = ((x - 0) ** 2) / (2 * (1 ** 2))y = 1 / (s * np.sqrt(2 * np.pi)) * np.exp(-a)return x, y, x.mean(), x.std()x = np.arange(-100, 100) # define range of x
x, y, u, s = normal(x, 10000)plt.plot(x, y, label=r'$\mu=%.2f,\ \sigma=%.2f$' % (u, s))
plt.legend()
plt.show()运行代码显示:
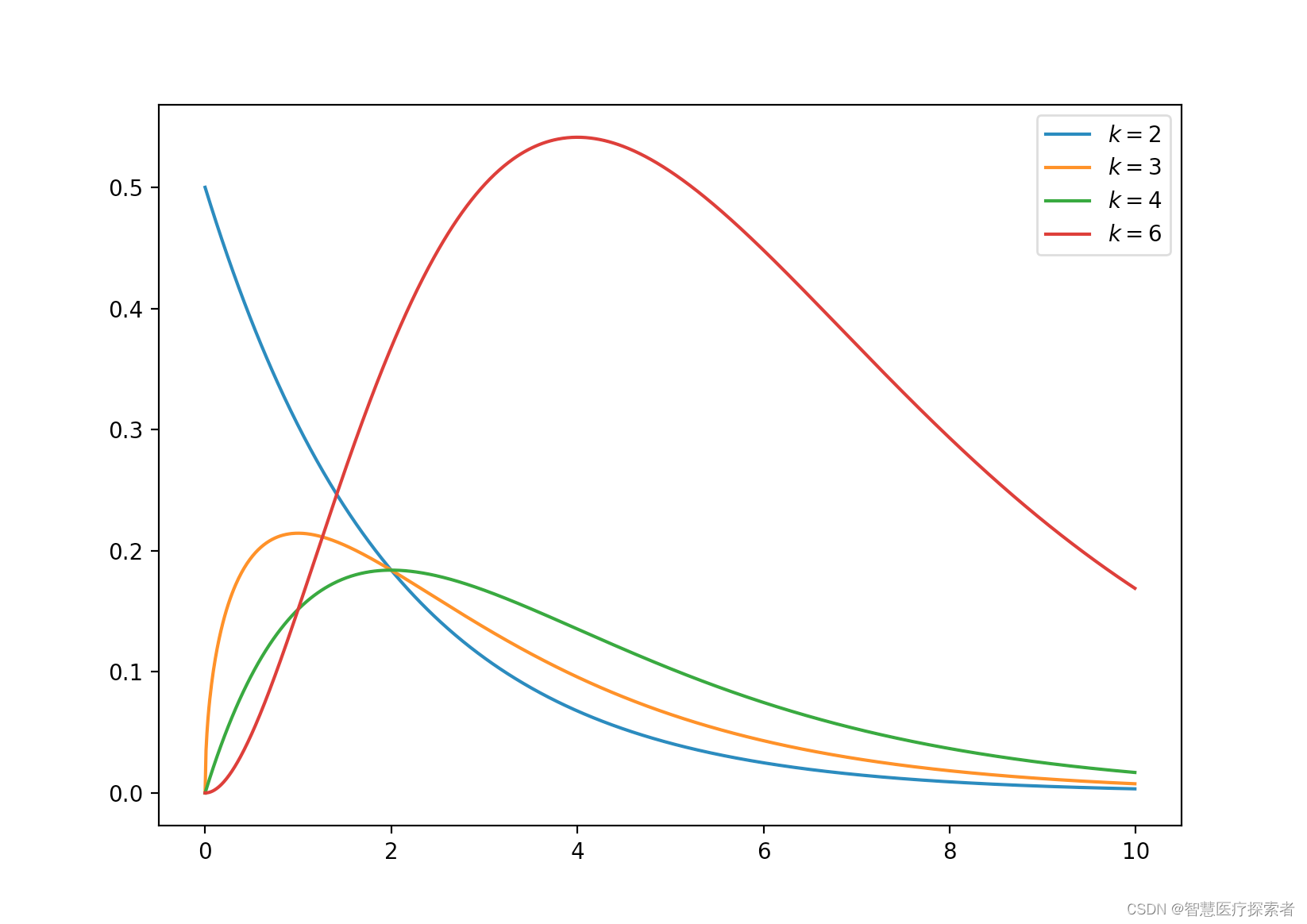
2.12 卡方分布(连续)
-
k 自由度的卡方分布是 k 个独立标准正态随机变量的平方和的分布。
-
卡方分布是 β 分布的特例
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef chi_squared(x, k):c = 1 / (2 ** (k/2)) * gamma_function(k//2)y = c * (x ** (k/2 - 1)) * np.exp(-x /2)return x, y, np.mean(y), np.std(y)for k in [2, 3, 4, 6]:x = np.arange(0, 10, 0.01, dtype=np.float)x, y, _, _ = chi_squared(x, k)plt.plot(x, y, label=r'$k=%d$' % (k))plt.legend()
plt.show()运行代码显示
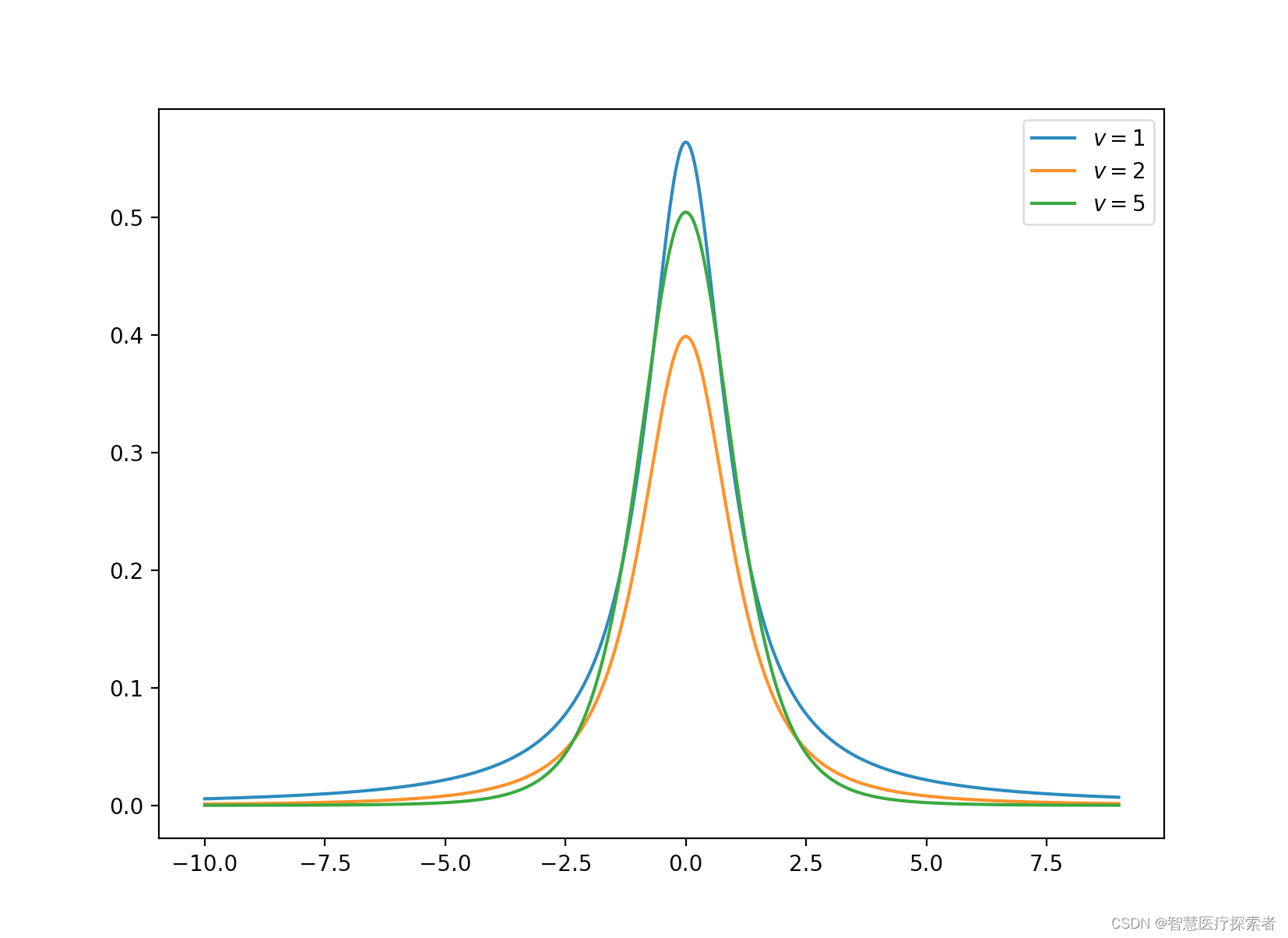
2.13 t 分布(连续)
t 分布是对称的钟形分布,与正态分布类似,但尾部较重,这意味着它更容易产生远低于平均值的值。
示例代码:
import numpy as np
from matplotlib import pyplot as pltdef gamma_function(n):cal = 1for i in range(2, n):cal *= ireturn caldef student_t(x, freedom, n):# divide [x.min(), x.max()] by nx = np.linspace(x.min(), x.max(), n)c = gamma_function((freedom + 1) // 2) \/ np.sqrt(freedom * np.pi) * gamma_function(freedom // 2)y = c * (1 + x**2 / freedom) ** (-((freedom + 1) / 2))return x, y, np.mean(y), np.std(y)for freedom in [1, 2, 5]:x = np.arange(-10, 10) # define range of xx, y, _, _ = student_t(x, freedom=freedom, n=10000)plt.plot(x, y, label=r'$v=%d$' % (freedom))plt.legend()
plt.show()运行代码显示
相关文章:

深度学习中的13种概率分布
1 概率分布概述 共轭意味着它有共轭分布的关系。 在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。 多…...

C#基础知识 - 操作数与运算符篇2
C#基础知识 - 操作数与运算符篇 4.2 运算符4.2.1 按操作数个数分类4.2.2 按运算类型分类4.2.3 对运算符 、-- 的使用4.2.4 关系运算符:>、 < 、> 、<、 ! 、4.2.5 逻辑运算符:&& || ! ^ & |4.2.6 位运算符:~ 、^、 &…...
第十五章总结
一.输入/输出流 1.输入流 InputStrema类是字节输入流的抽象类,它是所有字节输入流的父类。 该类中所有方法遇到错误都会引发IOException异常。 read()方法:从输入流中读取数据的下一个字节。返回0~255的int字节值。如果因为已经到达流末尾而没有可用的…...

音频I2S
前言 基于网上资料对相关概念做整理汇总,部分内容引用自文后文章。 学习目标:简单了解相关概念、相关协议。 1 概述 数字音频接口DAI,即Digital Audio Interfaces,顾名思义,DAI表示在板级或板间传输数字音频信…...

小程序中的合法域名的作用及条件有哪些?
小程序的合法域名是指小程序项目中使用的各种接口、资源文件等所在的域名。在小程序开发中,需要将这些域名添加到小程序后台的“开发设置”-“服务器域名”中进行配置,才能够正常使用。 合法域名的作用: 1.作为小程序请求的 API 服务器域名…...
SpringData JPA 整合Springboot
1.导入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...

打工人副业变现秘籍,某多/某手变现底层引擎-Stable Diffusion 黑白老照片上色修复
在这个时代,我们习惯于拥有高清、色彩丰富的照片,然而,那些古老的黑白色老照片由于年代的久远,往往会出现模糊、破损等现象。 那么今天要给大家介绍的是,用 Stable Diffusion 来修复老照片。 前段时间 ControlNet 的除了上线了“IP-Adapter”模型以外还增加另一个…...

第十三章总结
一.泛型 1.定义泛型类 泛型机制语法: 类名<T> 其中,T是泛型的名称,代表某一种类型。 【例13.6】创建带泛型的图书类 代码: 结果: 2.泛型的常规用法 (1)定义泛型类时声明多个变量 class MyClass<T1,T2…...

大模型应用_PrivateGPT
https://github.com/imartinez/privateGPT 1 功能 整体功能,想解决什么问题 搭建完整的 RAG 系统,与 FastGPT相比,界面比较简单。但是底层支持比较丰富,可用于知识库的完全本地部署,包含大模型和向量库。适用于保密级…...
[Android] ubuntu虚拟机上搭建 Waydroid 环境
1.安装虚拟机 略 2.安装waydroid Ubuntu/Debian and derivatives For Droidian and Ubuntu Touch, skip directly to the last step Install pre-requisites sudo apt install curl ca-certificates -y Add the official repository curl https://repo.waydro.id | sudo…...

LeedCode刷题---滑动窗口问题(二)
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、将X减到0的最小操作数 题目链接:将 x 减到 0 的最小操作数 题目描述 给你一个整数数组 nums 和一个整数 x 。每一…...
pycharm依赖管理(不要用pip freeze)
在使用python虚拟环境时,可以使用requirements.txt来管理当前项目的依赖。 注意,不要用 pip freeze > requirements.txt 这个命令,因为它会引入很多无关的包。 可以使用 pipreqs ./ --encodingutf-8 ./ 表示当前项目的目录࿰…...

[Kafka 常见面试题]如何保证消息的不重复不丢失
文章目录 Kafka1. Kafka如何保证不丢失消息?生产者数据的不丢失消费者数据的不丢失Kafka集群中的broker的数据不丢失 2. Kafka中的消息是否会丢失和重复消费?1. 消息发送2. 消息消费 3. Kafka 的设计是什么样的呢?4. 数据传输的事务定义有哪三…...
用法)
Java中System.setProperty()用法
Java中System.setProperty()用法 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入了解Java中的System.setProperty()方法,…...
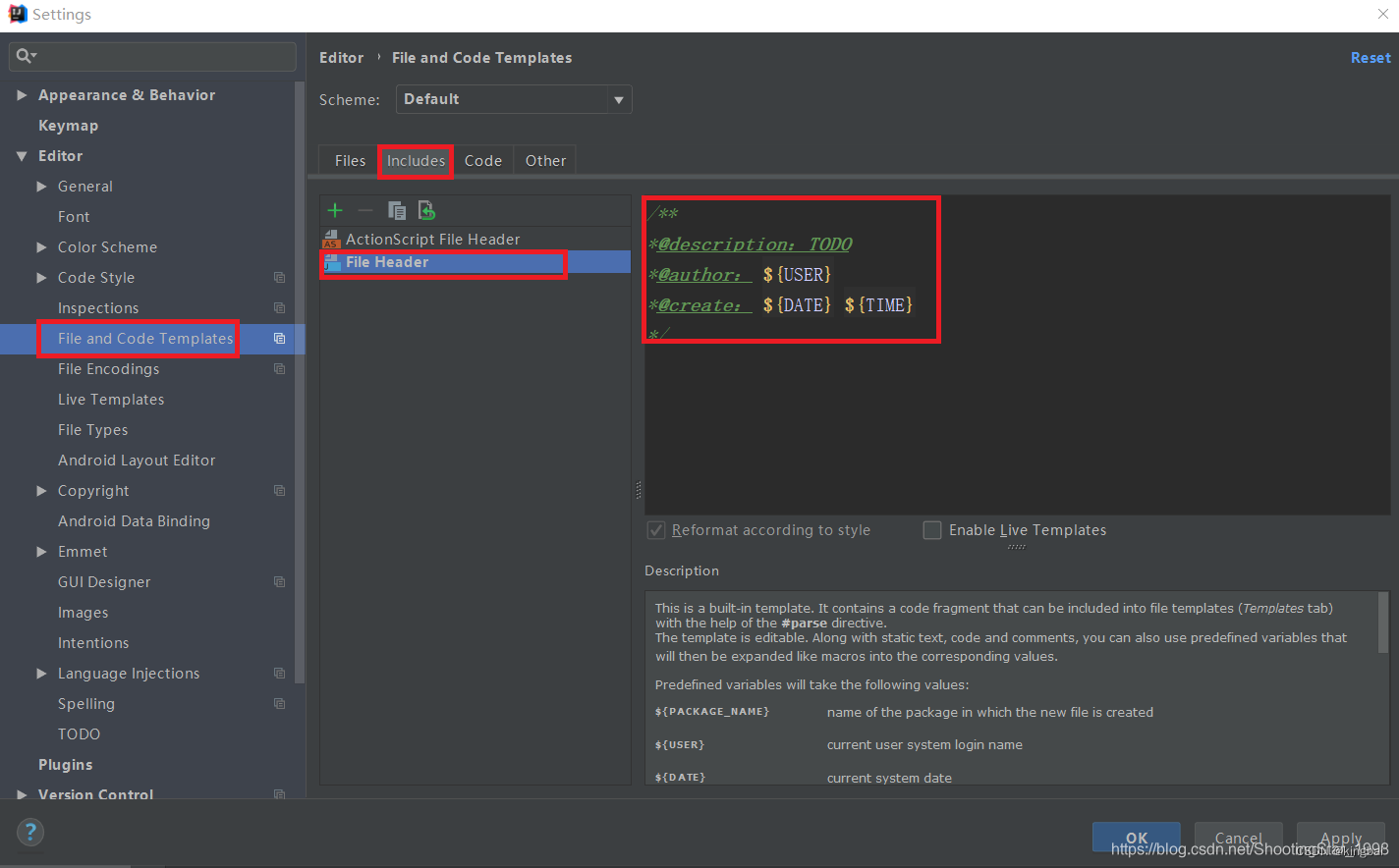
Eclipse 自动生成注解,如果是IDEA可以参考编译器自带模版进行修改
IDEA添加自动注解 左上角选择 File -> Settings -> Editor -> File and Code Templates; 1、添加class文件自动注解: /*** <b>Function: </b> todo* program: ${NAME}* Package: ${PACKAGE_NAME}* author: Jerry* date: ${YEA…...

微信小程序vant安装使用过程中遇到无法构建npm的问题
官网地址,然而如果完全按照这个教程来,实际上是缺少步骤的,需要补充一些步骤(参考https://www.bilibili.com/video/BV1vL41127Er) # 这步init就是补充的 npm init npm i vant/weapp -S --production# 剩下的按照vant的…...

[python]用python获取EXCEL文件内容并保存到DBC
目录 关键词平台说明背景所需库实现过程方法1.1.安装相关库2.代码实现 关键词 python、excel、DBC、openpyxl 平台说明 项目Valuepython版本3.6 背景 在搭建自动化测试平台的时候经常会提取DBC文件中的信息并保存为excel或者其他文件格式,用于自动化测试。本文…...

Spring Boot 如何配置 log4j2
Log4j2 介绍 Spring Boot 中默认使用 Logback 作为日志框架,接下来我们将学习如何在 Spring Boot 中集成与配置 Log4j2。在配置之前,我们需要知道的是 Log4j2 是 Log4j 的升级版,它在 Log4j 的基础上做了诸多改进: 异步日志&…...

如何安装docker
安装Docker的步骤取决于您使用的操作系统。以下是常见操作系统上安装Docker的基本步骤: 对于Linux: 更新软件包索引: sudo apt-get update安装允许apt通过HTTPS使用仓库的包: sudo apt-get install apt-transport-https ca-certificates cur…...

Linux 之 性能优化
uptime $ uptime -p up 1 week, 1 day, 21 hours, 27 minutes$ uptime12:04:11 up 8 days, 21:27, 1 user, load average: 0.54, 0.32, 0.23“12:04:11” 表示当前时间“up 8 days, 21:27,” 表示运行了多长时间“load average: 0.54, 0.32, 0.23”“1 user” 表示 正在登录…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
