java8实战 lambda表达式和函数式接口(上)
前言:
本博客对java8实战第三章的总结,也是上一篇博客行为化参数的延续,介绍一下函数式接口
Lambda表达式

lambda的表达式的结构由:参数,箭头,主体构成。
lambda示例

函数式接口:
先看上一篇博文最后一个例子如下:,用lambda例子来筛选苹果,其中仓库inventory包含了很多苹果Apple对象list,然后再根据red条件筛选红色苹果,我们对筛选的这个行为进行行为参数化,其中Predicate<T> p,这个就是一个函数式接口。
public interface Predicate<T> {boolean test(T t);
}public static <T> List<T> filter(<List<T> list, Predicate<T> p){List<T> result = new ArrayList<>();for(T e: list){if(p.test(e)){result.add(e);} }
}List<Apple> redAndHeavyApple = filterApples(inventory, (Apple apple) -> "red".equals(apple.getColor()));什么是函数式接口?简单来说,就是定义一个抽象方法的接口,如上面Predicate接口里面定义了一个抽象方法test,它就是函数式接口,就是这么简单。
那么函数式接口可以用来做什么?Lambda表示式允许你直接以内联形形式为函数式接口的抽象方法提供实现,并把整个表达式作为函数式接口的实例。简单来说,Lambda就是一个函数式接口的具体实现,而lambda主体部分就是函数式接口的抽象方法。
它的效果类似这样,以“等号”分割线的上下两部分一样的效果,而可以看到lambda表达式更简洁。
List<Apple> redAndHeavyApple = filterApples(inventory, (Apple apple) -> "red".equals(apple.getColor()));
===============================================
public class AppleRedPredicate implements Predicate {public boolean test(Apple apple) {return "red".equals(apple.getColor();}
}List<Apple> redAndHeavyApple = filterApples(inventory, new AppleRedAndHeavyPredicate());Java API也有其他的函数式接口:
public interface Comparator<T> {int compare(T o1, To2);
}public interface Runnable {void run();
}public interface ActionListener extends EventListener{void actionPerformed(ActionEvent e);
}public interface Callable<V>{V call();
}public interface PrivilegedAction<V>{T run();
}当前前面那个Predicate<T>接口也是.
如何使用lambda和函数式接口
书本举了一个"环绕执行模式"例子,环绕执行模式,在我看来就是,所有行为都是围绕执行处理过程,比如资源处理时候,打开一个资源(数据库或者文件),然后做一些处理,然后关闭操作,这过程中,中间这段处理过程就是重点。
如下,有一段代码式打开某个文件,并且读取一行并返回
public static String processFile() throws IOException{try (BufferdReader br = new BufferdReader(new FileReader("data.txt"))){return br.readLine();}
}这段代码式有局限的,就如第一篇博客所说,需求式不断变化的,如果需求改为读取两行,或者返回使用最频繁的词,那上面代码无法满足,那么一种就是不断创建新函数,每种函数处理不同情况,还有一种保持一个处理函数,但是处理函数的入参是行为参数,处理函数统一处理不同行为参数,也就是说处理的行为,体现在参数上,如使用lambda表达式来体现行为参数:
String result = processFile((BufferedReader br) -> br.readLine() + br.readLine());那么对应的,processFile入参就是函数式接口,所以还需要创建一个能匹配BufferReader->String的函数式接口:
@FunctionalInterface
public interface BufferedReaderProcessor {String process(BufferedReader b) throws IOException;
}然后processFile就变成了
public static String processFile(BufferedReaderProcessor p) throws IOException{try (BufferdReader br = new BufferdReader(new FileReader("data.txt"))){return p.process(br);}
}因此我们就得到一个很灵活的processFile,通过用lambda表达式来表达不同的行为:
读取一行:
String result = processFile((BufferedReader br) -> br.readLine());读取两行:
String result = processFile((BufferedReader br) -> br.readLine() + br.readLine());第三章剩下的部分下一篇博客继续讲。我个人感觉这种方式很灵活,我认为它也不是完全完美,其一就是要求行为参数代码量得少,个人感觉不适宜lambda写太多行为代码,我认为如果行为太过复杂反而用不同类来实现函数式接口,将入参变为不同类对象,反而代码可读性更好些。
参考文献:
《java8 实战》
相关文章:

java8实战 lambda表达式和函数式接口(上)
前言: 本博客对java8实战第三章的总结,也是上一篇博客行为化参数的延续,介绍一下函数式接口 Lambda表达式 lambda的表达式的结构由:参数,箭头,主体构成。 lambda示例 函数式接口: 先看上一篇…...
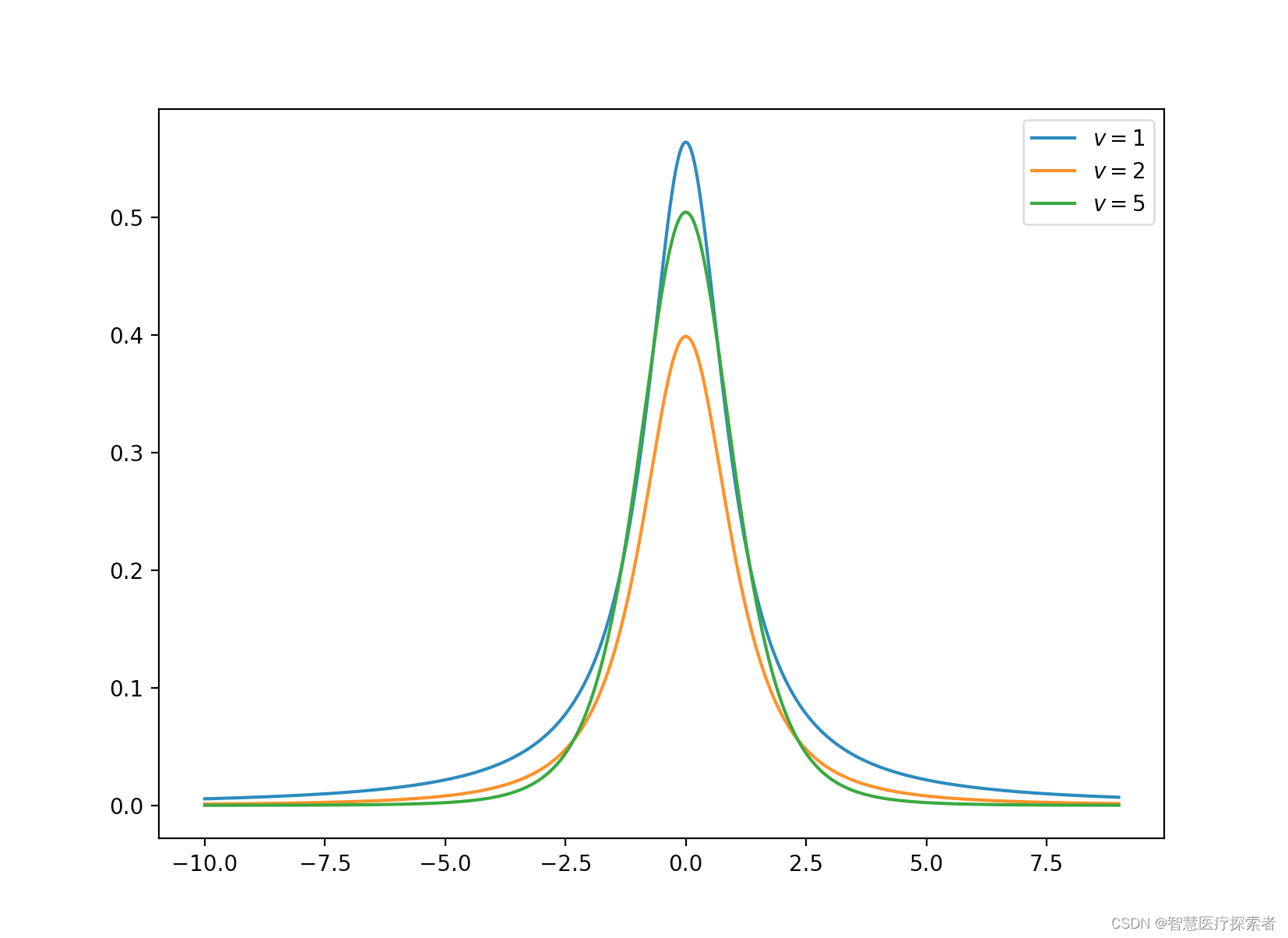
深度学习中的13种概率分布
1 概率分布概述 共轭意味着它有共轭分布的关系。 在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。 多…...

C#基础知识 - 操作数与运算符篇2
C#基础知识 - 操作数与运算符篇 4.2 运算符4.2.1 按操作数个数分类4.2.2 按运算类型分类4.2.3 对运算符 、-- 的使用4.2.4 关系运算符:>、 < 、> 、<、 ! 、4.2.5 逻辑运算符:&& || ! ^ & |4.2.6 位运算符:~ 、^、 &…...
第十五章总结
一.输入/输出流 1.输入流 InputStrema类是字节输入流的抽象类,它是所有字节输入流的父类。 该类中所有方法遇到错误都会引发IOException异常。 read()方法:从输入流中读取数据的下一个字节。返回0~255的int字节值。如果因为已经到达流末尾而没有可用的…...

音频I2S
前言 基于网上资料对相关概念做整理汇总,部分内容引用自文后文章。 学习目标:简单了解相关概念、相关协议。 1 概述 数字音频接口DAI,即Digital Audio Interfaces,顾名思义,DAI表示在板级或板间传输数字音频信…...

小程序中的合法域名的作用及条件有哪些?
小程序的合法域名是指小程序项目中使用的各种接口、资源文件等所在的域名。在小程序开发中,需要将这些域名添加到小程序后台的“开发设置”-“服务器域名”中进行配置,才能够正常使用。 合法域名的作用: 1.作为小程序请求的 API 服务器域名…...
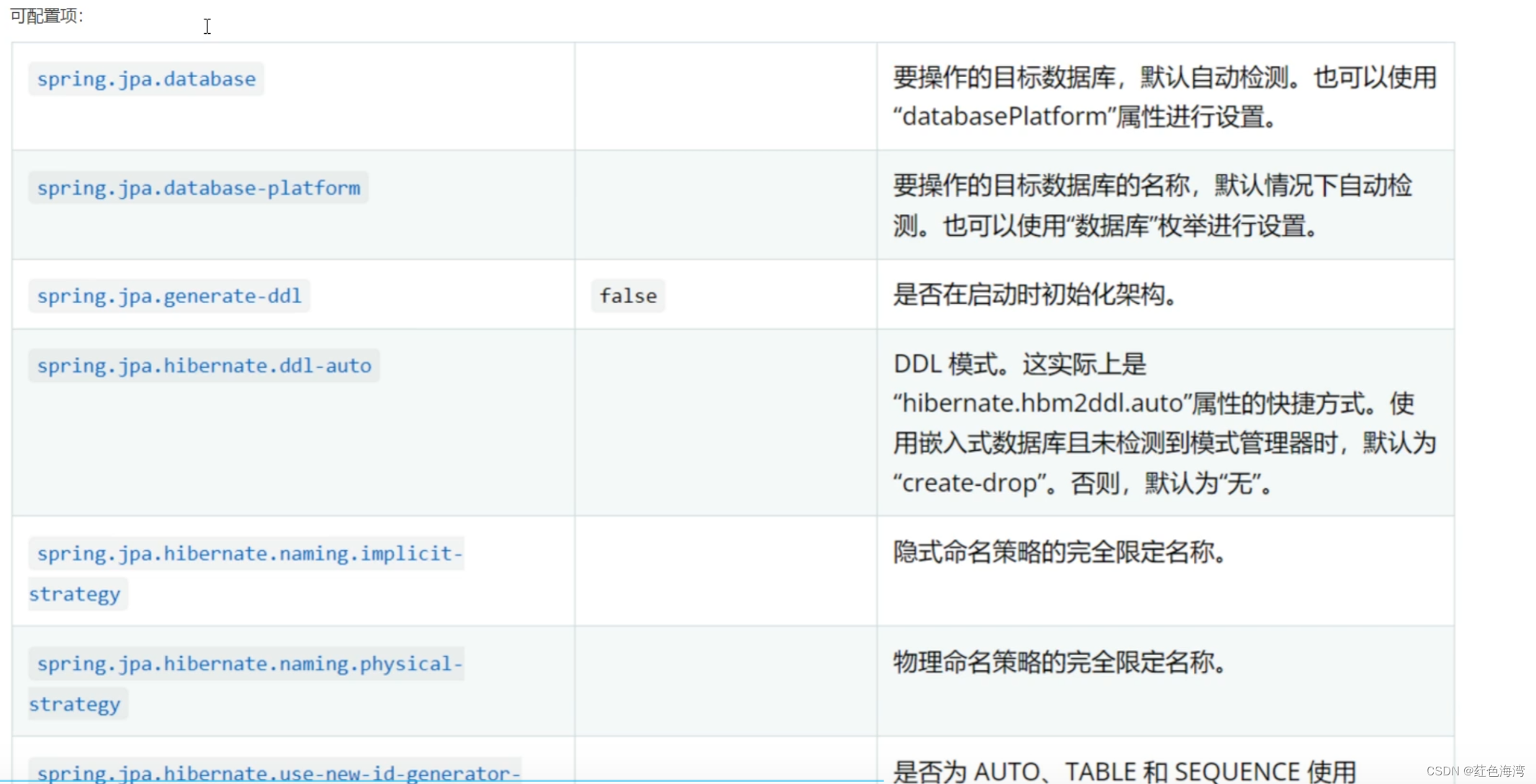
SpringData JPA 整合Springboot
1.导入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...

打工人副业变现秘籍,某多/某手变现底层引擎-Stable Diffusion 黑白老照片上色修复
在这个时代,我们习惯于拥有高清、色彩丰富的照片,然而,那些古老的黑白色老照片由于年代的久远,往往会出现模糊、破损等现象。 那么今天要给大家介绍的是,用 Stable Diffusion 来修复老照片。 前段时间 ControlNet 的除了上线了“IP-Adapter”模型以外还增加另一个…...

第十三章总结
一.泛型 1.定义泛型类 泛型机制语法: 类名<T> 其中,T是泛型的名称,代表某一种类型。 【例13.6】创建带泛型的图书类 代码: 结果: 2.泛型的常规用法 (1)定义泛型类时声明多个变量 class MyClass<T1,T2…...

大模型应用_PrivateGPT
https://github.com/imartinez/privateGPT 1 功能 整体功能,想解决什么问题 搭建完整的 RAG 系统,与 FastGPT相比,界面比较简单。但是底层支持比较丰富,可用于知识库的完全本地部署,包含大模型和向量库。适用于保密级…...
[Android] ubuntu虚拟机上搭建 Waydroid 环境
1.安装虚拟机 略 2.安装waydroid Ubuntu/Debian and derivatives For Droidian and Ubuntu Touch, skip directly to the last step Install pre-requisites sudo apt install curl ca-certificates -y Add the official repository curl https://repo.waydro.id | sudo…...

LeedCode刷题---滑动窗口问题(二)
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、将X减到0的最小操作数 题目链接:将 x 减到 0 的最小操作数 题目描述 给你一个整数数组 nums 和一个整数 x 。每一…...
pycharm依赖管理(不要用pip freeze)
在使用python虚拟环境时,可以使用requirements.txt来管理当前项目的依赖。 注意,不要用 pip freeze > requirements.txt 这个命令,因为它会引入很多无关的包。 可以使用 pipreqs ./ --encodingutf-8 ./ 表示当前项目的目录࿰…...

[Kafka 常见面试题]如何保证消息的不重复不丢失
文章目录 Kafka1. Kafka如何保证不丢失消息?生产者数据的不丢失消费者数据的不丢失Kafka集群中的broker的数据不丢失 2. Kafka中的消息是否会丢失和重复消费?1. 消息发送2. 消息消费 3. Kafka 的设计是什么样的呢?4. 数据传输的事务定义有哪三…...
用法)
Java中System.setProperty()用法
Java中System.setProperty()用法 大家好,我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天,让我们一起深入了解Java中的System.setProperty()方法,…...
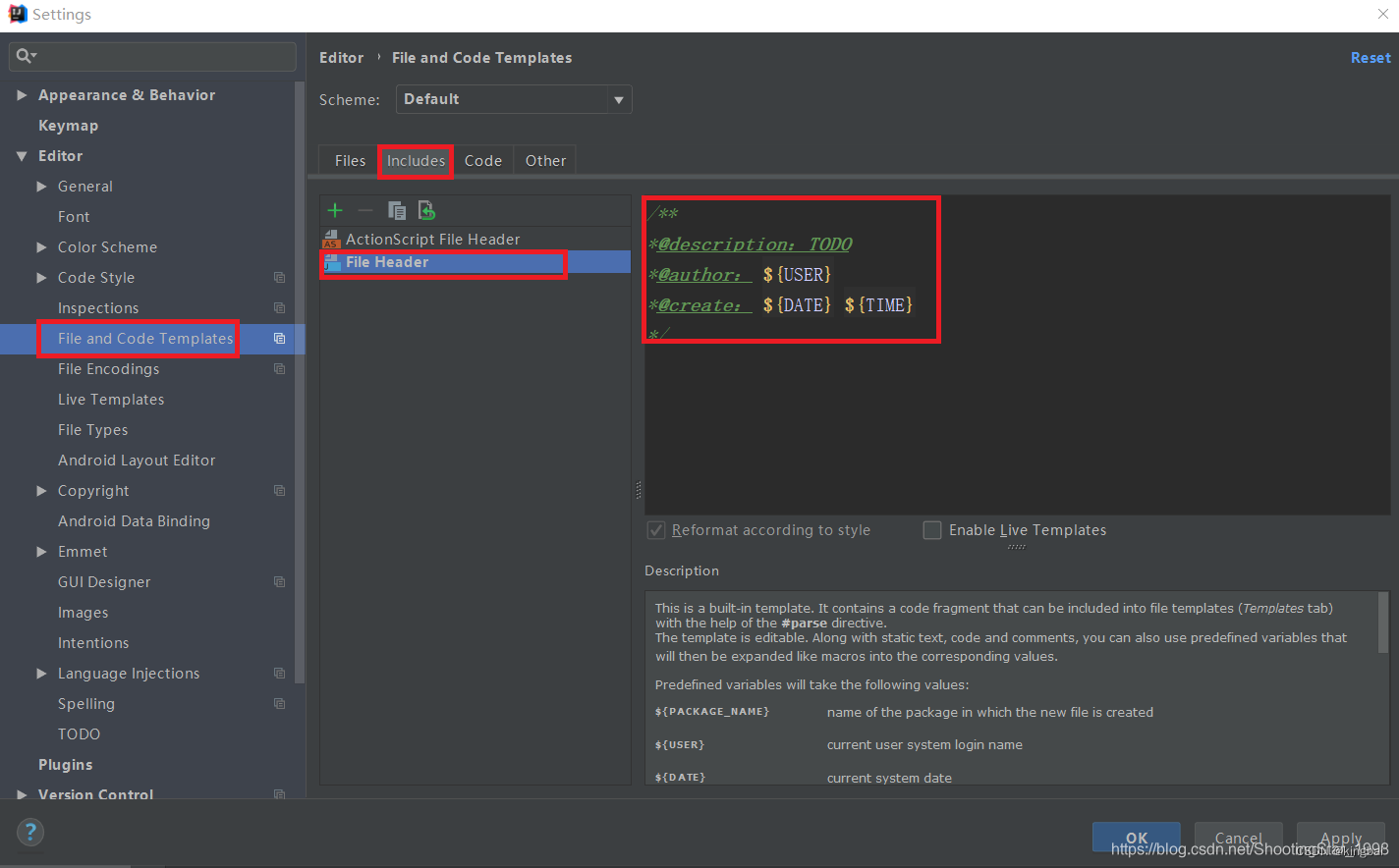
Eclipse 自动生成注解,如果是IDEA可以参考编译器自带模版进行修改
IDEA添加自动注解 左上角选择 File -> Settings -> Editor -> File and Code Templates; 1、添加class文件自动注解: /*** <b>Function: </b> todo* program: ${NAME}* Package: ${PACKAGE_NAME}* author: Jerry* date: ${YEA…...

微信小程序vant安装使用过程中遇到无法构建npm的问题
官网地址,然而如果完全按照这个教程来,实际上是缺少步骤的,需要补充一些步骤(参考https://www.bilibili.com/video/BV1vL41127Er) # 这步init就是补充的 npm init npm i vant/weapp -S --production# 剩下的按照vant的…...

[python]用python获取EXCEL文件内容并保存到DBC
目录 关键词平台说明背景所需库实现过程方法1.1.安装相关库2.代码实现 关键词 python、excel、DBC、openpyxl 平台说明 项目Valuepython版本3.6 背景 在搭建自动化测试平台的时候经常会提取DBC文件中的信息并保存为excel或者其他文件格式,用于自动化测试。本文…...

Spring Boot 如何配置 log4j2
Log4j2 介绍 Spring Boot 中默认使用 Logback 作为日志框架,接下来我们将学习如何在 Spring Boot 中集成与配置 Log4j2。在配置之前,我们需要知道的是 Log4j2 是 Log4j 的升级版,它在 Log4j 的基础上做了诸多改进: 异步日志&…...

如何安装docker
安装Docker的步骤取决于您使用的操作系统。以下是常见操作系统上安装Docker的基本步骤: 对于Linux: 更新软件包索引: sudo apt-get update安装允许apt通过HTTPS使用仓库的包: sudo apt-get install apt-transport-https ca-certificates cur…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...

C++ Saucer 编写Windows桌面应用
文章目录 一、背景二、Saucer 简介核心特性典型应用场景 三、生成自己的项目四、以Win32项目方式构建Win32项目禁用最大化按钮 五、总结 一、背景 使用Saucer框架,开发Windows桌面应用,把一个html页面作为GUI设计放到Saucer里,隐藏掉运行时弹…...
