京东体育用品销售数据分析与可视化系统
京东体育用品销售数据分析与可视化系统
- 前言
- 数据爬取模块
- 1. 数据爬取
- 2. 数据处理
- 3. 数据存储
- 数据可视化模块
- 1. 数据查看
- 2. 店铺商品数量排行
- 3. 整体好评率
- 4. 不同品牌市场占比
- 5. 品牌差评率排名
- 6. 品牌价格排名
- 7. 品牌评论数量分布
- 创新点
前言
在体育用品行业,了解市场销售数据是制定有效营销策略的重要一环。为了帮助体育用品企业更好地了解市场动态,我设计并实现了一套基于 Flask 和 Echarts 的体育用品销售数据分析与可视化系统。该系统主要分为数据爬取和数据可视化两个模块,每个模块下又包含多个子模块,以满足不同需求的数据分析。

数据爬取模块
1. 数据爬取
通过爬取京东体育用品的销售数据,我们能够获取到丰富的商品信息,包括品牌、价格、评价等数据。
2. 数据处理
爬取下来的数据可能存在一些杂乱无章的情况,因此在这个子模块中,对数据进行清洗和处理,确保数据的准确性和可用性。
3. 数据存储
处理后的数据需要进行存储,这里选择使用数据库进行数据的持久化存储,以便后续的分析和可视化。
数据可视化模块
1. 数据查看
通过数据查看功能,用户可以灵活选择不同的维度和指标,实时查看销售数据的变化趋势,帮助企业了解市场动态。
2. 店铺商品数量排行
展示不同店铺的商品数量排行,帮助企业了解各店铺在市场上的竞争力。
3. 整体好评率
通过可视化的方式展示体育用品整体好评率,为企业提供了解市场反馈的重要依据。
4. 不同品牌市场占比
分析不同品牌在市场上的份额,帮助企业制定品牌推广策略。
5. 品牌差评率排名
展示各品牌的差评率排名,帮助企业及时发现并解决品牌问题,提升产品质量。
6. 品牌价格排名
通过价格排名,企业可以了解各品牌产品在市场上的价格水平,为定价策略提供参考。
7. 品牌评论数量分布
分析品牌评论数量的分布情况,帮助企业发现市场的热门品牌和产品。
创新点
通过引入可视化大屏,本系统能够将复杂的销售数据以生动的图表形式呈现,使得数据更加直观和易懂。这种可视化方式不仅提高了数据分析的效率,也为企业决策提供了更直观的支持。同时,系统模块化的设计,使得用户可以根据需求选择特定功能,灵活应用于不同场景,满足多层次的数据分析需求。
通过这个体育用品销售数据分析与可视化系统,企业可以更加深入地了解市场状况,优化产品策略,提升市场竞争力,为企业的可持续发展提供有力支撑。
相关文章:

京东体育用品销售数据分析与可视化系统
京东体育用品销售数据分析与可视化系统 前言数据爬取模块1. 数据爬取2. 数据处理3. 数据存储 数据可视化模块1. 数据查看2. 店铺商品数量排行3. 整体好评率4. 不同品牌市场占比5. 品牌差评率排名6. 品牌价格排名7. 品牌评论数量分布 创新点 前言 在体育用品行业,了…...

【STM32】STM32学习笔记-EXTI外部中断(11)
00. 目录 文章目录 00. 目录01. 中断系统02. 中断执行流程03. STM32中断04. NVIC基本结构05. NVIC优先级分组06. EXTI简介07. EXTI基本结构08. AFIO复用IO口09. EXTI框图10. 计数器模块11. 旋转编码器简介12. 附录 01. 中断系统 中断:在主程序运行过程中࿰…...

CSS BFC详解
概念 BFC(Block Formatting Context)是CSS中的一个概念,用于描述一个独立的渲染区域,其中的元素按照一定规则进行布局和渲染。 BFC具有以下特性和作用 清除浮动:当一个元素的float属性设置为left或right时ÿ…...
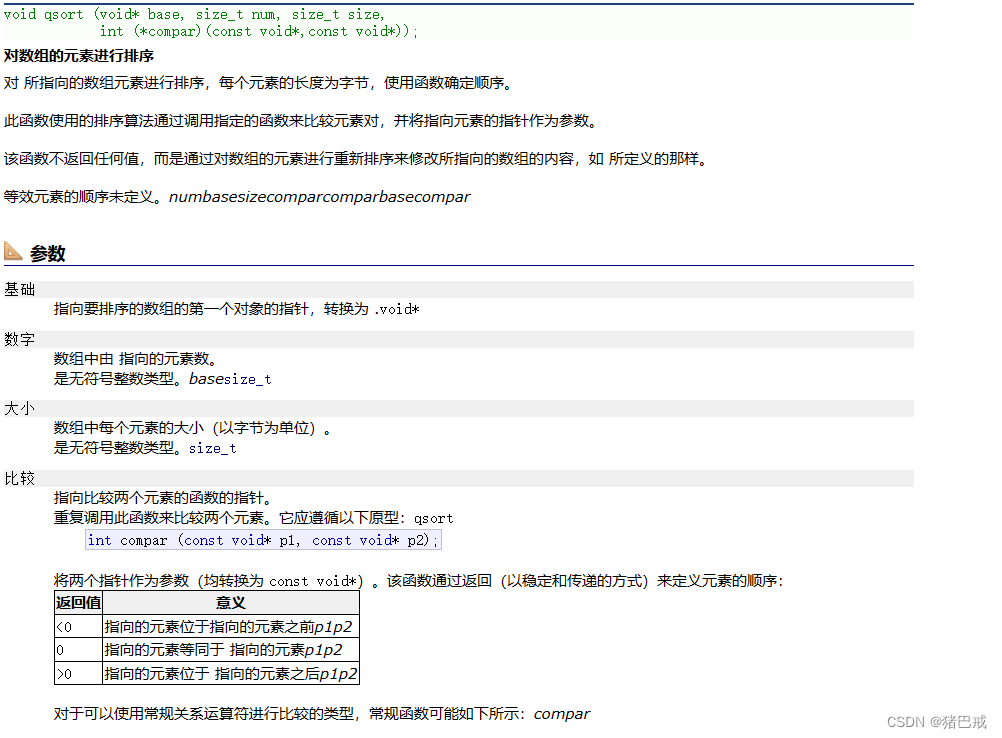
【C语言】实战项目——通讯录
引言 学会创建一个通讯录,对过往知识进行加深和巩固。 文章很长,要耐心学完哦! ✨ 猪巴戒:个人主页✨ 所属专栏:《C语言进阶》 🎈跟着猪巴戒,一起学习C语言🎈 目录 引言 实战 建…...

05 Rust 结构体
结构体 Rust 中的结构体(Struct)与元组(Tuple)都可以将若干个类型不一定相同的数据捆绑在一起形成整体,但结构体的每个成员和其本身都有一个名字,这样访问它成员的时候就不用记住下标了。 元组常用于非定…...
C语言预处理详解及其指令
预处理详解 1.预定义符号2.#define定义常量基本使用方法举例子如果在define定义的表示符后面加上分号会发生什么?用一下来解释 3. #define定义宏举例例1例2 4. 带有副作用的宏参数例如: 5. 宏替换的规则6. 宏函数的对比宏和函数的一个对比 7. #和##7.1 #运算符7.2 #…...
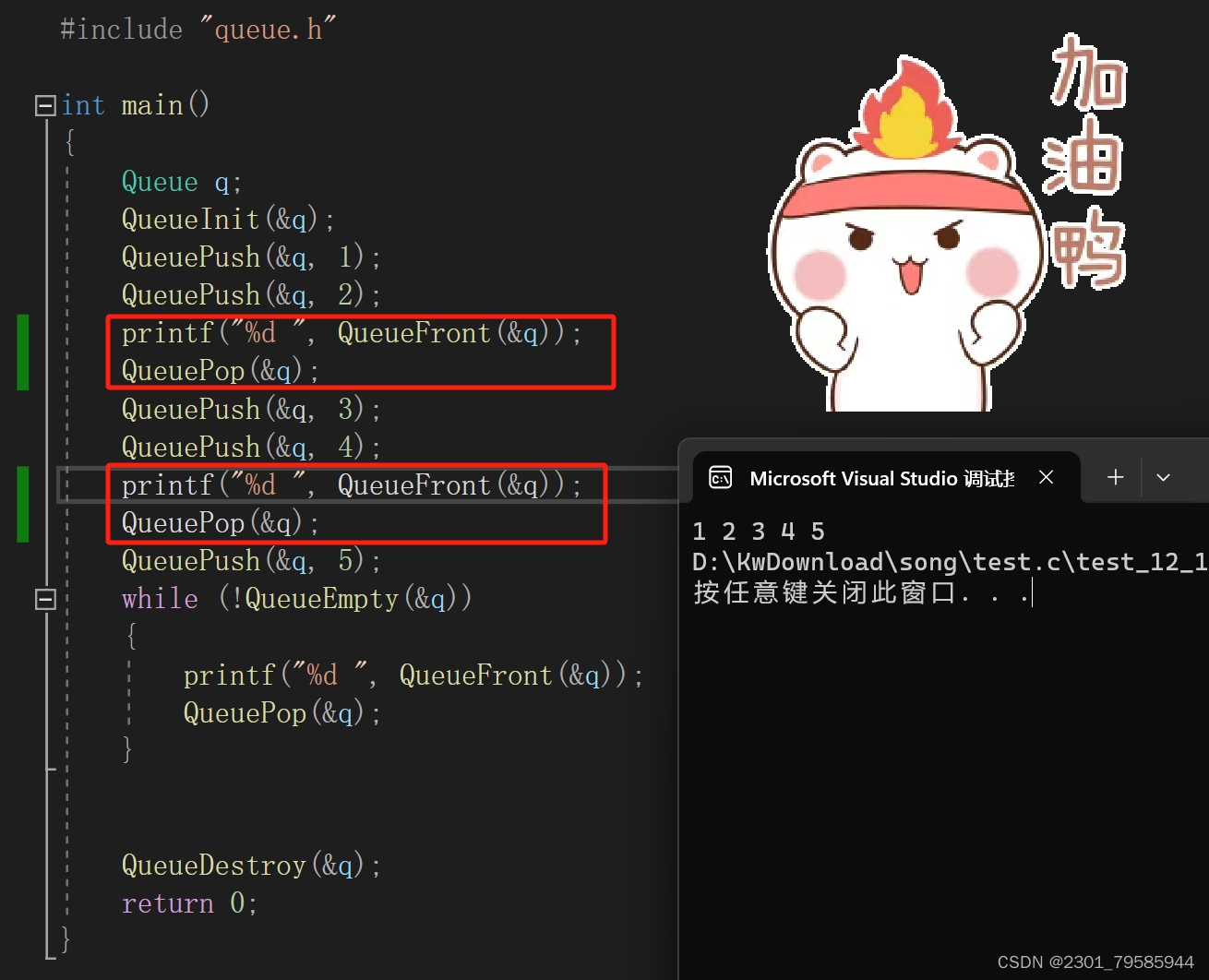
【数据结构—队列的实现】
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 一、队列 1.1队列的概念及结构 二、队列的实现 2.1头文件的实现—Queue.h 2.2源文件的实现—Queue.c 2.3源文件的测试—test.c 三、测试队列实际数据的展示 3.…...
ASP.NET MVC实战之权限拦截Authorize使用
1,具体的实现方法代码如下 public class CustomAuthorizeAttribute : FilterAttribute, IAuthorizationFilter{/// <summary>/// 如果需要验证权限的时候,就执行进来/// </summary>/// <param name"filterContext"></par…...

java8实战 lambda表达式和函数式接口(上)
前言: 本博客对java8实战第三章的总结,也是上一篇博客行为化参数的延续,介绍一下函数式接口 Lambda表达式 lambda的表达式的结构由:参数,箭头,主体构成。 lambda示例 函数式接口: 先看上一篇…...
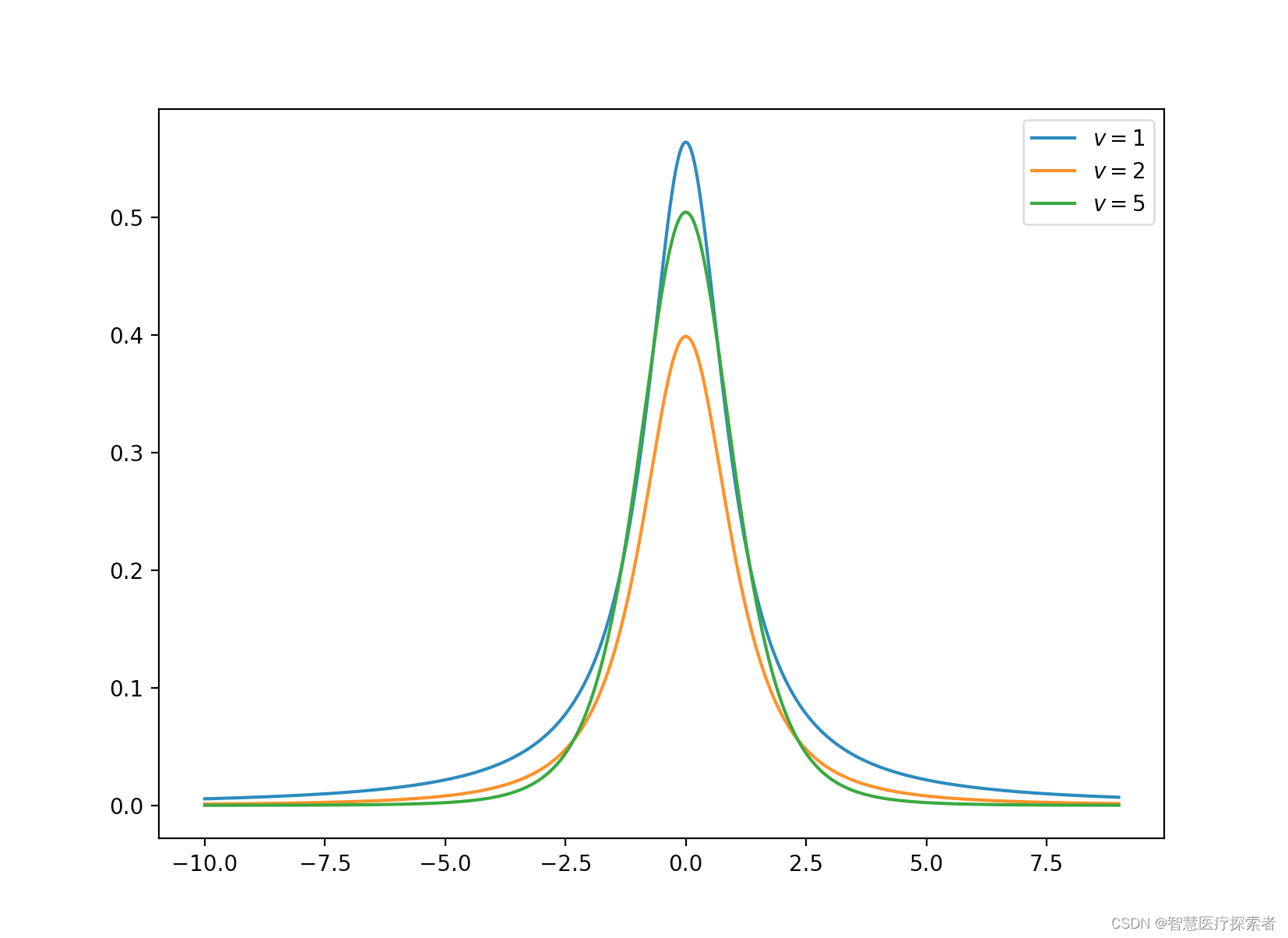
深度学习中的13种概率分布
1 概率分布概述 共轭意味着它有共轭分布的关系。 在贝叶斯概率论中,如果后验分布 p(θx)与先验概率分布 p(θ)在同一概率分布族中,则先验和后验称为共轭分布,先验称为似然函数的共轭先验。 多…...

C#基础知识 - 操作数与运算符篇2
C#基础知识 - 操作数与运算符篇 4.2 运算符4.2.1 按操作数个数分类4.2.2 按运算类型分类4.2.3 对运算符 、-- 的使用4.2.4 关系运算符:>、 < 、> 、<、 ! 、4.2.5 逻辑运算符:&& || ! ^ & |4.2.6 位运算符:~ 、^、 &…...
第十五章总结
一.输入/输出流 1.输入流 InputStrema类是字节输入流的抽象类,它是所有字节输入流的父类。 该类中所有方法遇到错误都会引发IOException异常。 read()方法:从输入流中读取数据的下一个字节。返回0~255的int字节值。如果因为已经到达流末尾而没有可用的…...

音频I2S
前言 基于网上资料对相关概念做整理汇总,部分内容引用自文后文章。 学习目标:简单了解相关概念、相关协议。 1 概述 数字音频接口DAI,即Digital Audio Interfaces,顾名思义,DAI表示在板级或板间传输数字音频信…...

小程序中的合法域名的作用及条件有哪些?
小程序的合法域名是指小程序项目中使用的各种接口、资源文件等所在的域名。在小程序开发中,需要将这些域名添加到小程序后台的“开发设置”-“服务器域名”中进行配置,才能够正常使用。 合法域名的作用: 1.作为小程序请求的 API 服务器域名…...
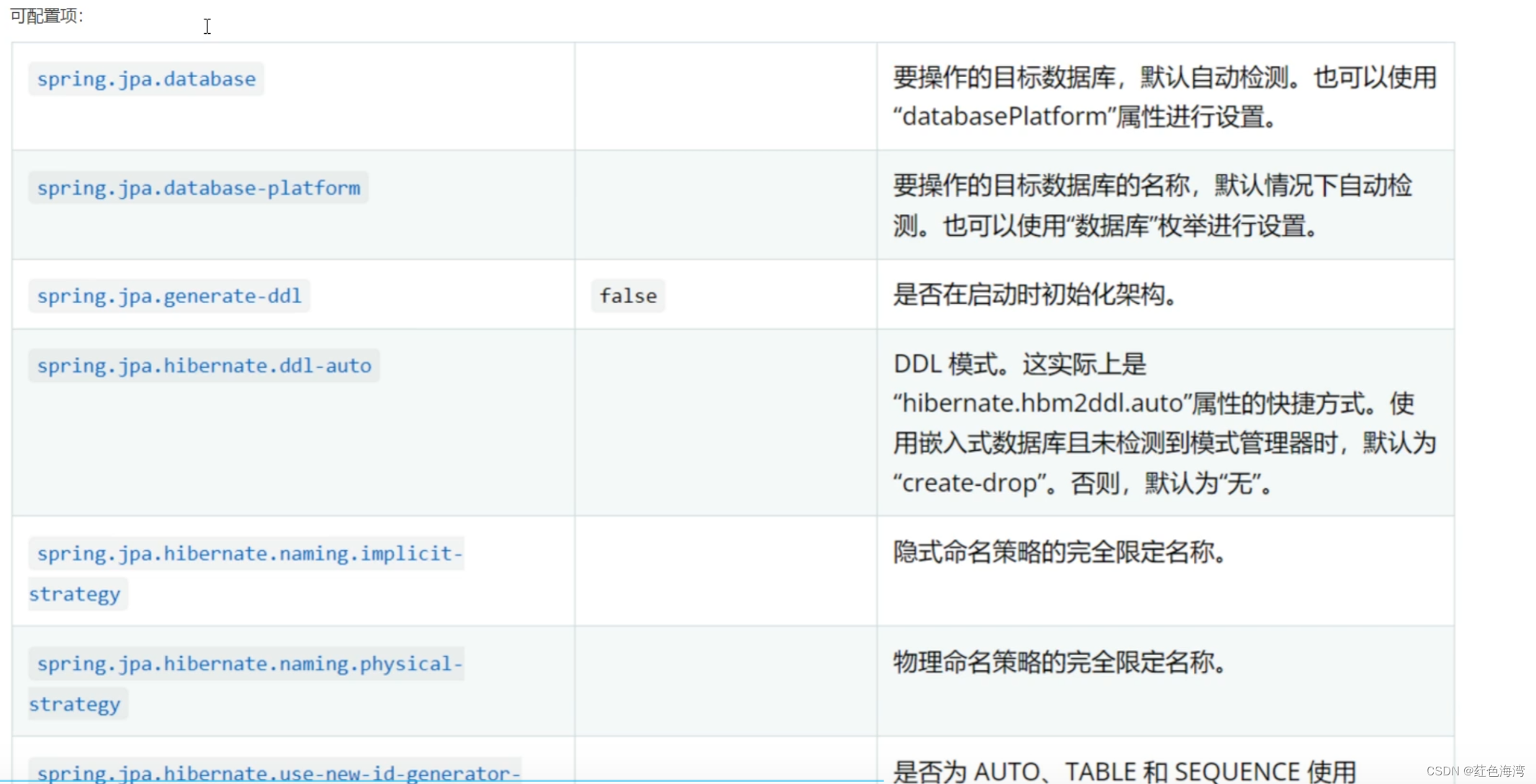
SpringData JPA 整合Springboot
1.导入依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...

打工人副业变现秘籍,某多/某手变现底层引擎-Stable Diffusion 黑白老照片上色修复
在这个时代,我们习惯于拥有高清、色彩丰富的照片,然而,那些古老的黑白色老照片由于年代的久远,往往会出现模糊、破损等现象。 那么今天要给大家介绍的是,用 Stable Diffusion 来修复老照片。 前段时间 ControlNet 的除了上线了“IP-Adapter”模型以外还增加另一个…...

第十三章总结
一.泛型 1.定义泛型类 泛型机制语法: 类名<T> 其中,T是泛型的名称,代表某一种类型。 【例13.6】创建带泛型的图书类 代码: 结果: 2.泛型的常规用法 (1)定义泛型类时声明多个变量 class MyClass<T1,T2…...

大模型应用_PrivateGPT
https://github.com/imartinez/privateGPT 1 功能 整体功能,想解决什么问题 搭建完整的 RAG 系统,与 FastGPT相比,界面比较简单。但是底层支持比较丰富,可用于知识库的完全本地部署,包含大模型和向量库。适用于保密级…...
[Android] ubuntu虚拟机上搭建 Waydroid 环境
1.安装虚拟机 略 2.安装waydroid Ubuntu/Debian and derivatives For Droidian and Ubuntu Touch, skip directly to the last step Install pre-requisites sudo apt install curl ca-certificates -y Add the official repository curl https://repo.waydro.id | sudo…...

LeedCode刷题---滑动窗口问题(二)
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、将X减到0的最小操作数 题目链接:将 x 减到 0 的最小操作数 题目描述 给你一个整数数组 nums 和一个整数 x 。每一…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
