快速排序(一)
目录
快速排序(hoare版本)
初级实现
问题改进
中级实现
时空复杂度
高级实现
三数取中
快速排序(hoare版本)
初级实现
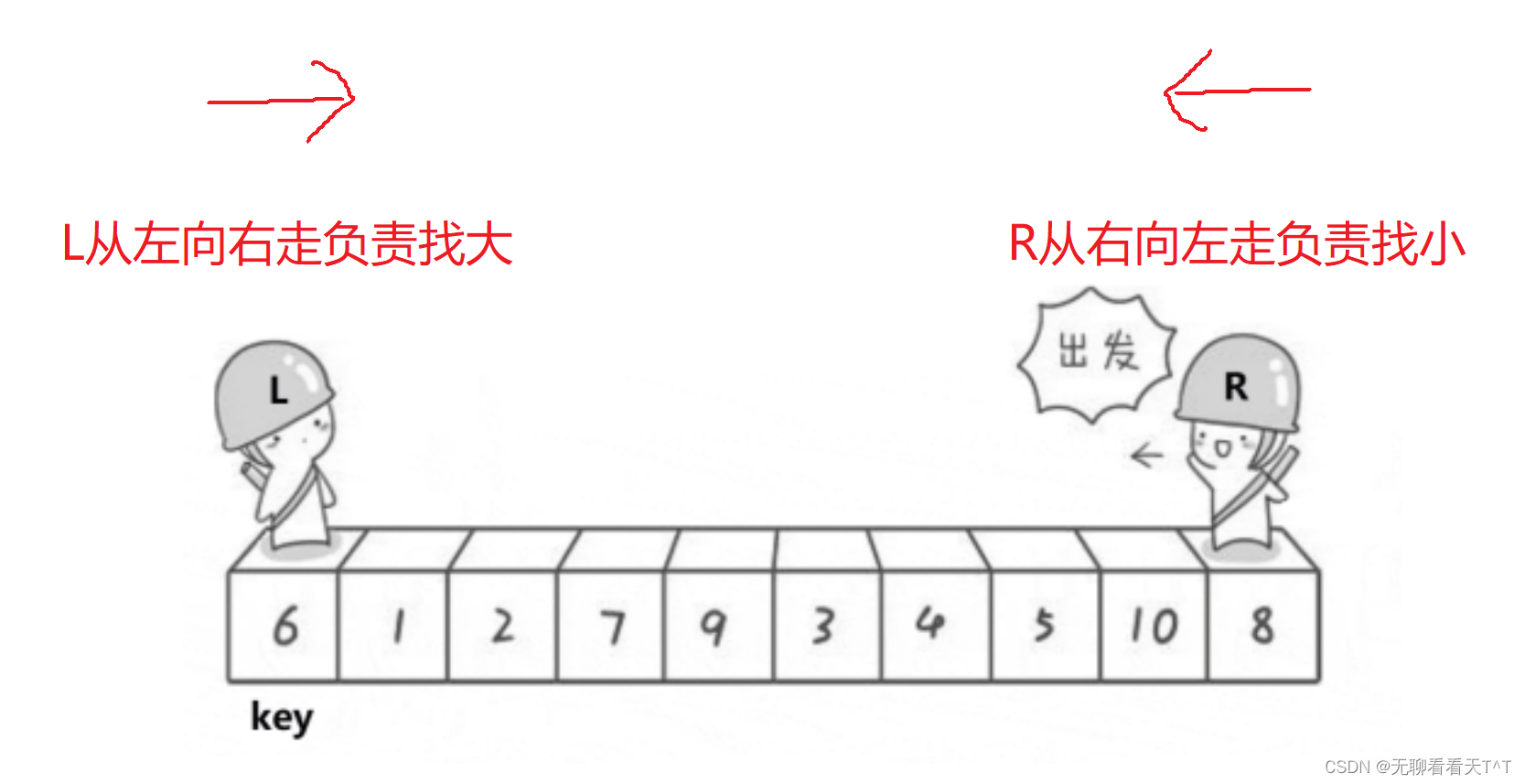
int left = begin; //数组首元素下标
int right = end; //数组尾元素下标
int keyi = begin; //即可以是首元素下标、也可以是尾元素下标,一般来说是首元素下标2、right和left开始自己的寻找任务,当a[right] > a[keyi],right就--继续向左走,当a[left] < a[keyi],left就++继续向右走,当二者都在找的过程中在某一位置停下时(两个while循环均结束),交换此时的a[left]和a[right]:
void QuickSort(int* a, int begin, int end)
{int left = begin, right = end;int keyi = begin;// 右边找小while (a[right] > a[keyi]){--right;}// 左边找大while (a[left] < a[keyi]){++left;}Swap(&a[left], &a[right]);}3、当left与right相遇即left == right时,此时元素的值一定小于基准元素的值,所以交换当前元素与基准元素的位置(因为我们要做的就是将小于基准元素的数放在左边,大于的放在右边):

void QuickSort(int* a, int begin, int end)
{int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (a[right] > a[keyi]){--right;}// 左边找大while (a[left] < a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);
}关于“为什么相遇位置一定会比基准元素小”的解释:
因为我们规定右边先走(当然你也可以让左基准元素是数组尾元素然后左边先走,这里就不再分析了),这样就会有两种相遇的情况:
①right遇到left,right没找到比基准元素小的,一直走,找到时停下,然后left向右走,当二者相遇即right ==left时停下(原因我们后面会将),所处位置的元素的值小于基准元素:
②left遇到right,right先走,找到小于基准元素的位置停下,left开始找比基准元素大的,没有找到,一直走,遇到right停下,相遇位置是right,前面说过此时的位置应该是小于基准元素的位置(“right先走,找到小于基准元素的位置停下”):
至此,我们快速排序的初级实现已经完成了,接下来就是处理我们遗留的一些问题了:
问题改进
1、产生原因:有时我们写的代码只适用于部分数据,但是换成其它数据时就会出错,为了保证我们代码的通用性,我们要进行多次的用例测试,比如我们将数组换为{6,1,2,5,4,6,9,7,10,8}:
可以发现,之前的代码并不能让right和left相遇,又因为我们规定right先走,所以我们为了能让二者相遇,需要保证left永远不会超过right,故在a[right] > a[keyi]之前加上left < right,即left < right && a[right] >= a[keyi],left也是一样的道理:
void QuickSort(int* a, int begin, int end) {int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] > a[keyi]){--right;}// 左边找大while (left < right && a[left] < a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]); }
2、产生原因:当我们将基准元素换到数组的中的某个位置时,它左侧的元素经过一系列检查与交换的操作后已经全部是小于基准元素的元素,右边的元素也已经全部是大于基准元素的元素,现在我们要做的就是将左右两边的元素均变为有序,当左右两边均有序时该数组就完全有序(原因自己想去😡)这就需要用到递归思想了(在前面我们说过hoare版本的快排是基于二叉树思想的),当我们尝试对上面的数组开始递归操作时,如果还是原来的代码就会出现下图所示的问题:
可以发现, 原本我们是想通过右递归将右侧大于基准元素的几个元素变为有序,但可以看到的是只有当a[right] == 4时才会停下,此时就已经在左递归的范围内了,因此为了保证不会越界,我们还需要为a[right] > a[keyi]加上一个"=",即a[right] >= a[keyi],左递归也是一样的道理:
void QuickSort(int* a, int begin, int end) {int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]); }
中级实现
至此,我们开始进行递归操作,关于递归的过程如下图所示:
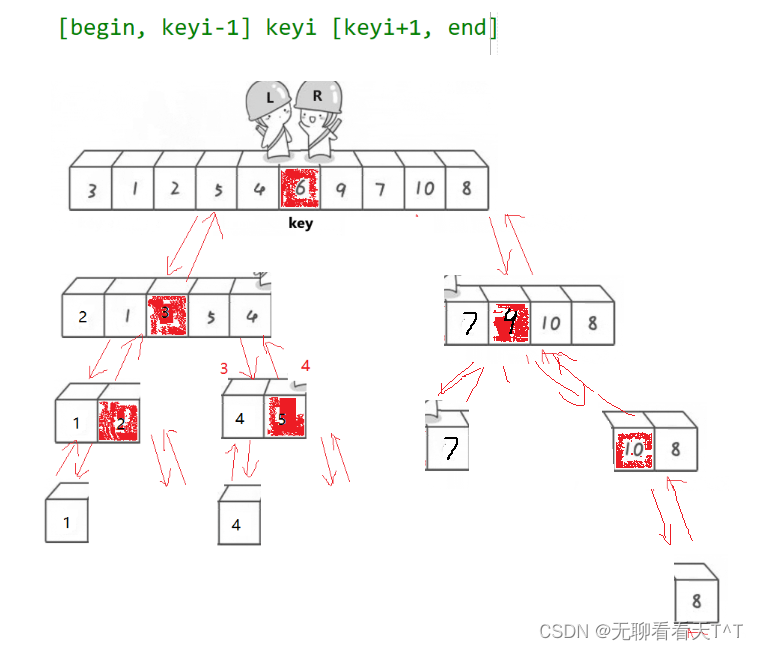
关于递归的代码也不再过多解释,自行理解即可:
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}
以上就是一个“较为”完整的快速排序的代码
时空复杂度
最坏时间复杂度:O(N^2)(当数组已经降序有序或升序有序时,此时基准元素一直位于首元素或尾元素,n个元素要进行n次快速排序才能将当前的顺序改变,n*n)
最好时间复杂度:O(N*logN)(每次划分都能将数组均匀地分成两个接近子数组,N个元素要进行logN次的排序,N*logN)
空间复杂度:O(logN)或O(N)(在递归过程中需要使用栈来保存函数调用信息,所以快速排序的空间复杂度取决于递归调用的层数。在最坏情况下,递归调用栈可能达到O(n)的空间复杂度,最好的空间复杂度为O(logn))
高级实现
当面对有序队列时,快速排序的效率确实会降低。这是因为快速排序的分区操作通常选择一个基准元素,并将小于等于基准的元素放在左侧,大于基准的元素放在右侧。如果输入数据已经有序,那么每次分区后只能将一个元素移到正确位置上,而剩余部分仍然需要进行递归调用。为了应对这种情况,可以采取以下方法来提高快速排序在有序队列上的效率:
随机化选择基准:通过随机选择基准值可以降低出现最坏情况(即已经有序)的概率。这样可以增加快速排序处理无序数据时的性能。
三数取中法:使用三数取中法来选择合适的基准值。从待排序数组中选取头、尾和中间位置上的三个数,并将它们按照大小顺序排列。然后选取其中位数作为划分子数组(即作为枢纽),以避免最坏情况发生。
插入排序优化:当待排序子数组长度较小时(比如小于某个阈值),可以切换到插入排序算法进行处理。插入算法对局部有序数据表现良好,在长度较短的子数组上可以提高排序效率。
优化递归调用:通过限制递归深度或者使用尾递归优化等方法,减少对有序数据的不必要处理。
这些方法可以在特定情况下提高快速排序算法在有序队列上的性能,但需要根据具体场景选择合适的策略。
三数取中
注意事项:获取的是下标为begin、midi、end的三个元素中的中位数(非最多,非最小)
完整代码如下:
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi; //返回a[midi] < a[midi] < a[end]else if (a[begin] > a[end])return begin; //返回a[end] < a[begin] < a[midi]elsereturn end; //返回a[begin] < a[end] < a[midi]}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi; //返回a[end] < a[mid] < a[begin]else if (a[begin] < a[end])return begin; //返回a[midi] < a[begin] < a[end]else return end; //返回a[midi] < a[end] < a[begin]}
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}~over~
相关文章:
快速排序(一)
目录 快速排序(hoare版本) 初级实现 问题改进 中级实现 时空复杂度 高级实现 三数取中 快速排序(hoare版本) 历史背景:快速排序是Hoare于1962年提出的一种基于二叉树思想的交换排序方法 基本思想:…...
GO的sql注入盲注脚本
之间学习了go的语法 这里就开始go的爬虫 与其说是爬虫 其实就是网站的访问如何实现 因为之前想通过go写sql注入盲注脚本 发现不是那么简单 这里开始研究一下 首先是请求网站 这里貌似很简单 package mainimport ("fmt""net/http" )func main() {res, …...
写好ChatGPT提示词原则之:清晰且具体(clear specific)
ChatGPT 的优势在于它允许用户跨越机器学习和深度学习的复杂门槛,直接利用已经训练好的模型。然而,即便是这些先进的大型语言模型也面临着上下文理解和模型固有局限性的挑战。为了最大化这些大型语言模型(LLM)的潜力,关…...
Java实现快速排序及其动图演示
快速排序(Quicksort)是一种基于分治思想的排序算法。它通过选择一个基准元素,将数组分为两个子数组,其中一个子数组的所有元素都小于基准元素,另一个子数组的所有元素都大于基准元素,然后递归地对这两个子数…...
iClient3D 图元操作
1. S3MTilesLayer,S3M(Spatial 3D Model)图层类 S3MTilesLayer,S3M(Spatial 3D Model)图层类,通过该图层实现加载三维切片缓存,包括倾斜摄影模型、BIM模型、点云数据、精细模型、矢量数据、符号等。 那S3MTilesLayer中针对图元的…...

从0到1!开发小白快速入门腾讯云数据库
在这个海量数据大爆发的时代,一个单一的开源数据库产品往往很难直接满足企业的业务需求,在某些场景下,无论是性能、安全还是稳定性,都面临着各种各样的问题。 你在工作中也有这样的烦恼的话,一定是因为你还没有使用过…...

Golang清晰代码指南
发挥易读和易维护软件的好处 - 第一部分 嗨,开发者们,清晰的代码是指编写易于阅读、理解和维护的软件代码。它是遵循一组原则和实践,优先考虑清晰性、简单性和一致性的代码。清晰的代码旨在使代码库更易管理,减少引入错误的可能性…...

C语言 文件I/O(备查)
所有案列 跳转到其他。 文件打开 FILE* fopen(const char *filename, const char *mode); 参数:filename:指定要打开的文件名,需要加上路径(相对、绝对路径)mode:指定文件的打开模式 返回值:成…...
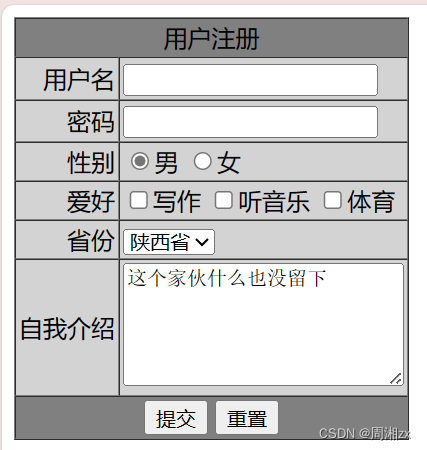
web(HTML之表单练习)
使用HTML实现该界面: 要求如下: 用户名为文本框,名称为 UserName,长度为 15,最大字符数为 20。 密码为密码框,名称为 UserPass,长度为 15,最大字符数为 20。 性别为两个单选按钮&a…...

通过对象轮换实现 LRU 缓存结构
文章目录 通过两个对象轮换,按照是否访问实现内容长久保存rollup 的缓存实现 export default function (max) { //max 缓存容量var num, curr, prev;var limit max || 1;function keep(key, value) {if (num > limit) {prev curr; // 超过容量时当前对象变成缓…...
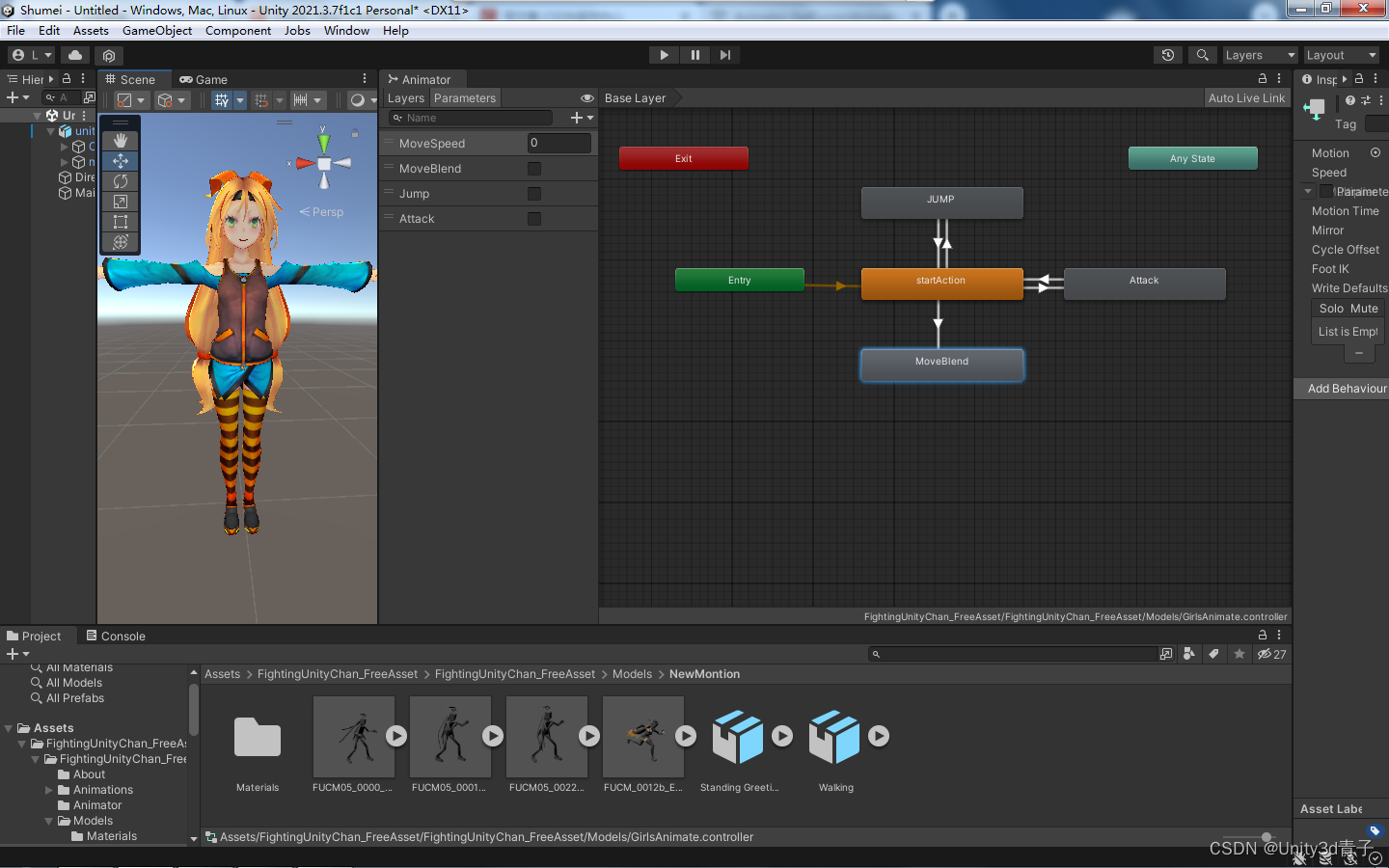
【Unity动画】综合案例完结-控制角色动作播放+声音配套
这个案例实现的动作并不复杂,主要包含一个 跳跃动作、攻击动作、还有一个包含三个动画状态的动画混合树。然后设置三个参数来控制切换。 状态机结构如下: 完整代码 using System.Collections; using System.Collections.Generic; using UnityEngine;pu…...
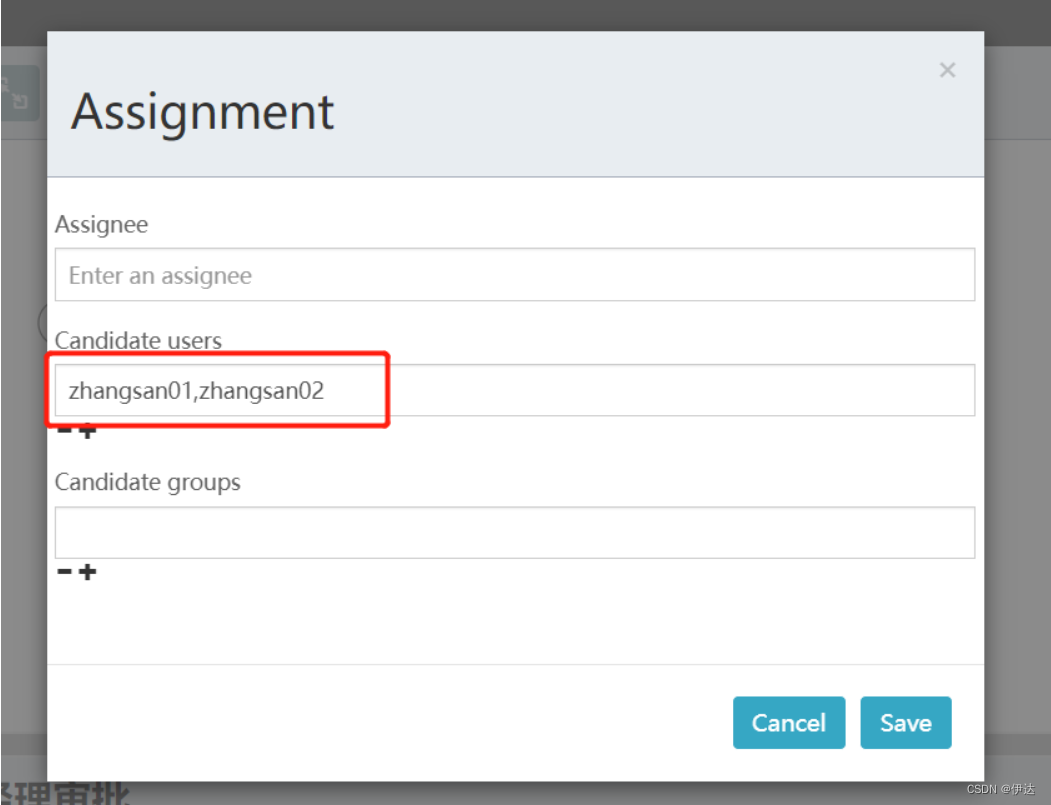
【工作流Activiti】任务组
1、Candidate-users候选人 1.1、需求 在流程定义中在任务结点的assignee固定设置任务负责人,在流程定义时将参与者固定设置在.bpmn文件中,如果要临时变更任务负责人则需要修改流程定义,系统扩展性很差,针对这种情况,我…...
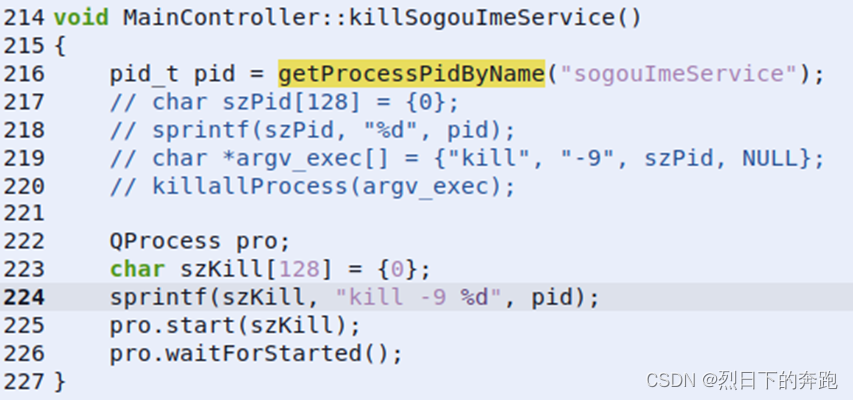
桌面概率长按键盘无法连续输入问题
问题描述:概率性长按键盘无法连续输入文本 问题定位: 系统按键流程分析 图一 系统按键流程 按键是由X Server接收的,这一点只要明白了X Window的工作机制就不难理解了。X Server在接收到按键后,会转发到相应程序的窗口中。在窗…...
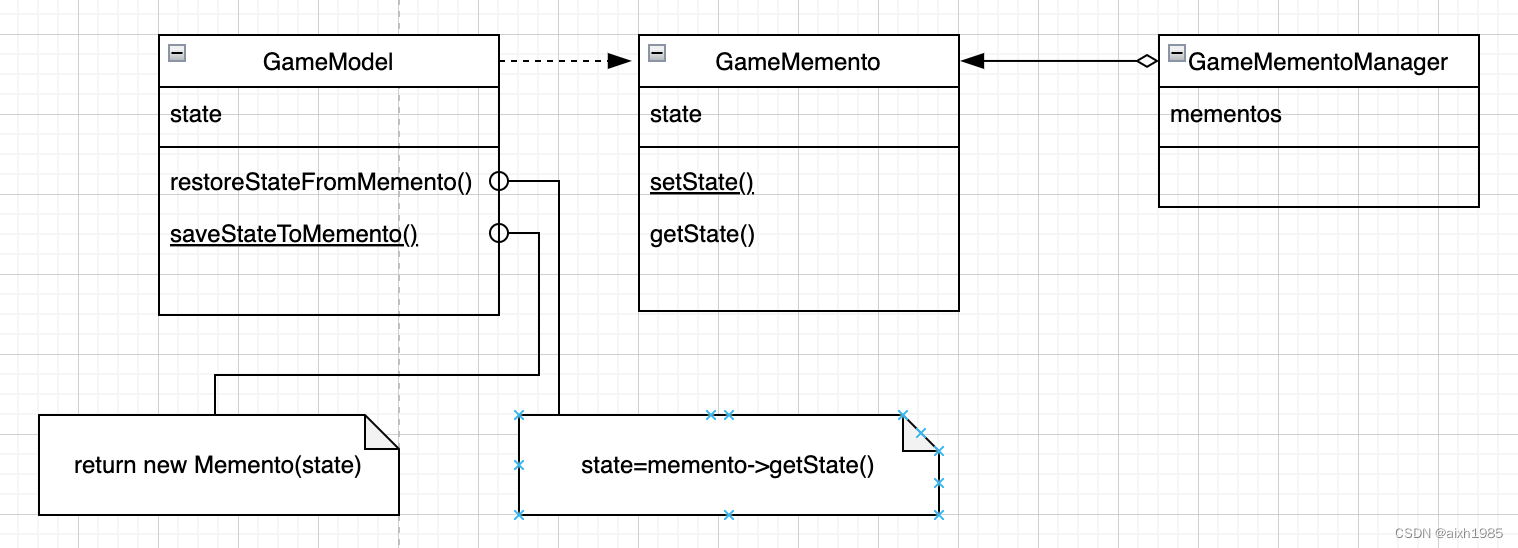
用23种设计模式打造一个cocos creator的游戏框架----(十九)备忘录模式
1、模式标准 模式名称:备忘录模式 模式分类:行为型 模式意图:在不破坏封装性的前提下捕获一个对象的内部状态,并在对象之外保存这个状态。这样以后就可以将对象恢复到原先保存的状态 结构图: 适用于: …...

动手学深度学习-自然语言处理-预训练
词嵌入模型 将单词映射到实向量的技术称为词嵌入。 为什么独热向量不能表达词之间的相似性? 自监督的word2vec。 word2vec将每个词映射到一个固定长度的向量,这些向量能更好的表达不同词之间的相似性和类比关系。 word2vec分为两类,两类…...
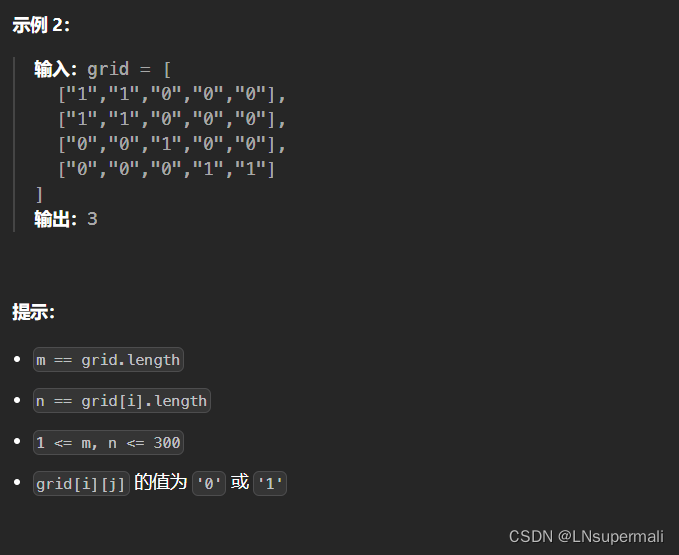
力扣200. 岛屿数量(java DFS解法)
Problem: 200. 岛屿数量 文章目录 题目描述思路解题方法复杂度Code 题目描述 思路 该问题可以归纳为一类遍历二维矩阵的题目,此类中的一部分题目可以利用DFS来解决,具体到本题目: 1.我们首先要针对于二维数组上的每一个点,尝试展…...
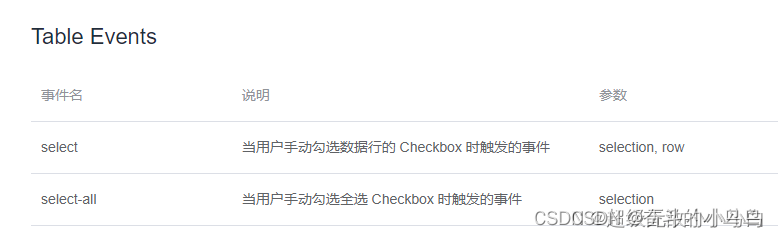
解决el-table组件中,分页后数据的勾选、回显问题?
问题描述: 1、记录一个弹窗点击确定按钮后,table列表所有勾选的数据信息2、再次打开弹窗,回显勾选所有保存的数据信息3、遇到的bug:切换分页,其他页面勾选的数据丢失;点击确认只保存当前页的数据࿱…...
web网络安全
web安全 一,xss 跨站脚本攻击(全称Cross Site Scripting,为和CSS(层叠样式表)区分,简称为XSS)是指恶意攻击者在Web页面中插入恶意javascript代码(也可能包含html代码),当用户浏览网页之时&…...

若依 ruoyi-vue3 集成aj-captcha实现滑块、文字点选验证码
目录 0. 前言0.1 说明 1. 后端部分1.1 添加依赖1.2. 修改 application.yml1.3. 新增 CaptchaRedisService 类1.4. 添加必须文件1.5. 移除不需要的类1.6. 修改登录方法1.7. 新增验证码开关获取接口1.8. 允许匿名访问 2. 前端部分(Vue3)2.1. 新增依赖 cryp…...

安卓10 flutter webview 回退会闪退
现象 在安卓10设备上,访问了webview页面后,回退到其他页面后,大概率会闪退,请查看issuses https://github.com/flutter/flutter/issues/78405 解决思路:在回退前,先把webview销毁掉,重新生成一个…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...





