【六大排序详解】开篇 :插入排序 与 希尔排序
插入排序 与 希尔排序
六大排序之二
- 插入排序 与 希尔排序
- 1 排序
- 1.1排序的概念
- 2 插入排序
- 2.1 插入排序原理
- 2.2 排序步骤
- 2.3 代码实现
- 3 希尔排序
- 3.1 希尔排序原理
- 3.2 排序步骤
- 3.3 代码实现
- 4 时间复杂度分析
- Thanks♪(・ω・)ノ
- 下一篇文章见!!!!!!!
1 排序
1.1排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
排序存在稳定性,稳定性是评估排序的重要标准。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
排序可以概括为两大类 、六大排序:
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
这篇文章我们先介绍插入排序。
2 插入排序
2.1 插入排序原理
生活中最常见的插入排序就是扑克牌,我们一张一张的拿出来,比较然后放在合适位置。所用思想就是插入排序:
把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列 。

2.2 排序步骤
- 从第一个元素开始,默认已经有序
- 取后一个元素tmp ,开始向前扫描
- (升序)如果有序序列的最后一个元素大于tmp , 有序序列结尾下标向前移动
- 重复 3 步骤,直到有序序列最后一个元素小于tmp
- 插入tmp在该有序序列后。
- 再取数组下一个元素,重复 1-5 步骤
2.3 代码实现
// 插入排序
void InsertSort(int* a, int n) {for (int i = 0; i < n - 1; i++) {int end = i;//记录有序部分的最后下标int tmp = a[end + 1];//被排序数while (end >= 0) {if (a[end] > tmp) {//如果有序部分最大值大于被排序数,有序下标--a[end + 1] = a[end];end--;}else//如果有序部分最大值小于被排序数,直接退出。break;}//在比被排序数小的有序部分后赋值a[end + 1] = tmp;}
}
功能实现效果,非常nice。

直接插入排序的特性总结:
- 元素集合越接近有序,直接插入排序算法的时间效率越高。
- 时间复杂度:O(N^2) 。
- 空间复杂度:O(1),它是一种稳定的排序算法
- 稳定性:稳定
3 希尔排序
3.1 希尔排序原理
希尔排序法又称缩小增量法。希尔排序法的基本思想是:先选定一个整数,把待排序文件中所有记录分成个组,所有距离为的记录分在同一组内,并对每一组内的记录进行排序。然后,取,重复上述分组和排序的工作。当到达=1时,所有记录在统一组内排好序。
根据插入排序的特性 元素集合越接近有序,直接插入排序算法的时间效率越高。,我们进行多次不同gap的插入排序,使其逐渐有序。进而时间复杂度更低。
插入排序可以视为特殊的希尔排序。
3.2 排序步骤
- 选定gap值,并分组进行预排序
- 每组进行插入排序,使序列变得更加有序。
- gap值变小(务必保证最后一次是gap==1)
- 重复 1 - 3 步骤,直到gap为1。
- 排序完成。

3.3 代码实现
// 希尔排序
void ShellSort(int* a, int n) {int gap = n;//设置初始gap值while (gap > 1) {gap = gap / 2;//每次除2 直至为 1for (int i = 0; i < n - gap; i++) {//每组插入排序int end = i;int tmp = a[end + gap];while (end >= 0) {if (a[end] > tmp) {a[end + gap] = a[end];end -= gap;}elsebreak;}a[end + gap] = tmp;//结束后赋值}}
}
运行查看效果,very good!

希尔排序的特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 - 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
希尔排序的时间复杂度都不固定:
4 时间复杂度分析
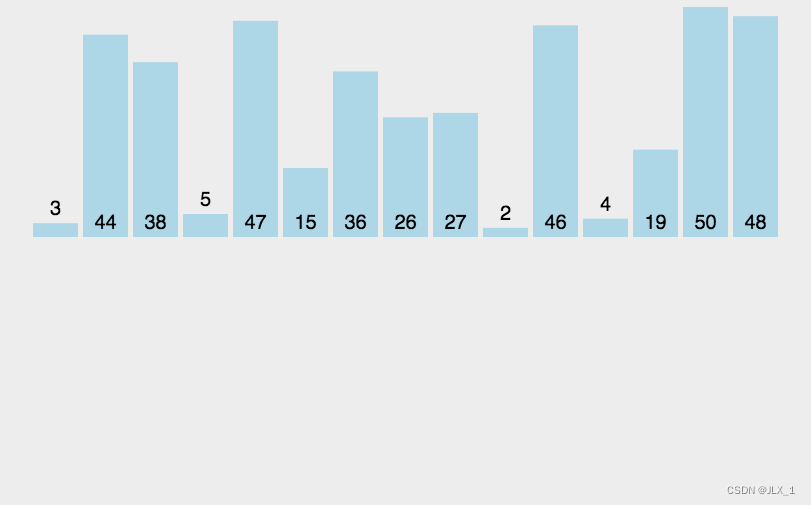
我们设计一个100000个数据测试函数,来检测一下插入排序,希尔排序的时间复杂度(以冒泡排序为对照组)。
请看下面测试效果:

这里希尔排序有非常明显的优势,运算非常之快,其次为插入排序。普通的冒泡排序在这里就像蝼蚁一般。
至于希尔排序的时间复杂度目前还没有证明。大概为n^1.3。下面是殷老师的观点。

Thanks♪(・ω・)ノ
下一篇文章见!!!!!!!
相关文章:

【六大排序详解】开篇 :插入排序 与 希尔排序
插入排序 与 希尔排序 六大排序之二 插入排序 与 希尔排序1 排序1.1排序的概念 2 插入排序2.1 插入排序原理2.2 排序步骤2.3 代码实现 3 希尔排序3.1 希尔排序原理3.2 排序步骤3.3 代码实现 4 时间复杂度分析 Thanks♪(・ω・)ノ下一篇文章见&am…...

凸优化问题求解
这里写目录标题 1. 线性规划基本定理2.单纯形法2.1 转轴运算 3. 内点法3.1 线性规划的内点法 1. 线性规划基本定理 首先我们指出,线性规划均可等价地化成如下标准形式 { min c T x , s . t A x b , x ⪰ 0 , \begin{align}\begin{cases}\min~c^Tx,\\\mathrm{s.…...
文件操作入门指南
目录 一、为什么使用文件 二、什么是文件 2.1 程序文件 2.2 数据文件 2.3 文件名 三、文件的打开和关闭 3.1 文件指针 3.2 文件的打开和关闭 四、文件的顺序读写 编辑 🌻深入理解 “流”: 🍂文件的顺序读写函数介绍: …...

Axure之交互与情节与一些实例
目录 一.交互与情节简介 二.ERP登录页到主页的跳转 三.ERP的菜单跳转到各个页面的跳转 四.省市联动 五.手机下拉加载 今天就到这里了,希望帮到你哦!!! 一.交互与情节简介 "交互"通常指的是人与人、人与计算机或物体…...
)
【数据库设计和SQL基础语法】--连接与联接--多表查询与子查询基础(二)
一、子查询基础 1.1 子查询概述 子查询是指在一个查询语句内部嵌套另一个查询语句的过程。子查询可以嵌套在 SELECT、FROM、WHERE 或 HAVING 子句中,用于从数据库中检索数据或执行其他操作。子查询通常返回一个结果集,该结果集可以被包含它的主查询使用…...
Android studio中导入opencv库
具体opencv库的导入流程参考链接:Android Studio开发之路 (五)导入OpenCV以及报错解决 一、出现的错误:NullPointerException: Cannot invoke “java.io.File.toPath()” because “this.mySdkLocation” is null 解决办法&#…...
_基础知识)
Linux(1)_基础知识
第一部分 一、Linux系统概述 创始人:芬兰大学大一的学生写的Linux内核,李纳斯托瓦兹。 Linux时unix的类系统; 特点:多用户 多线程的操作系统; 开源操作系统; 开源项目:操作系统,应用…...

网络相关面试题
简述 TCP 连接的过程(淘系) 参考答案: TCP 协议通过三次握手建立可靠的点对点连接,具体过程是: 首先服务器进入监听状态,然后即可处理连接 第一次握手:建立连接时,客户端发送 syn 包…...

Vue2面试题:说一下对跨域的理解?
http请求分为两大类:普通http请求(如百度请求)和ajax请求(跨域是出现在ajax请求) 同源策略:在浏览器发起ajax请求时,当前的网址和被请求的网址协议、域名、端口号必须完全一致,目的是…...

Axure中如何使用交互样式交互事件交互动作情形
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《产品经理如何画泳道图&流程图》 ⛺️ 越努力 ,越幸运 目录 一、Axure中交互样式 1、什么是交互样式? 2、交互样式的作用? 3、Axure中如何…...
)
1112. 迷宫(DFS之连通性模型)
1112. 迷宫 - AcWing题库 一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n∗n 的格点组成,每个格点只有2种状态,.和#,前者表示可以通行后者表示不能通行。 同时当Extense处在某个格点时,他只…...
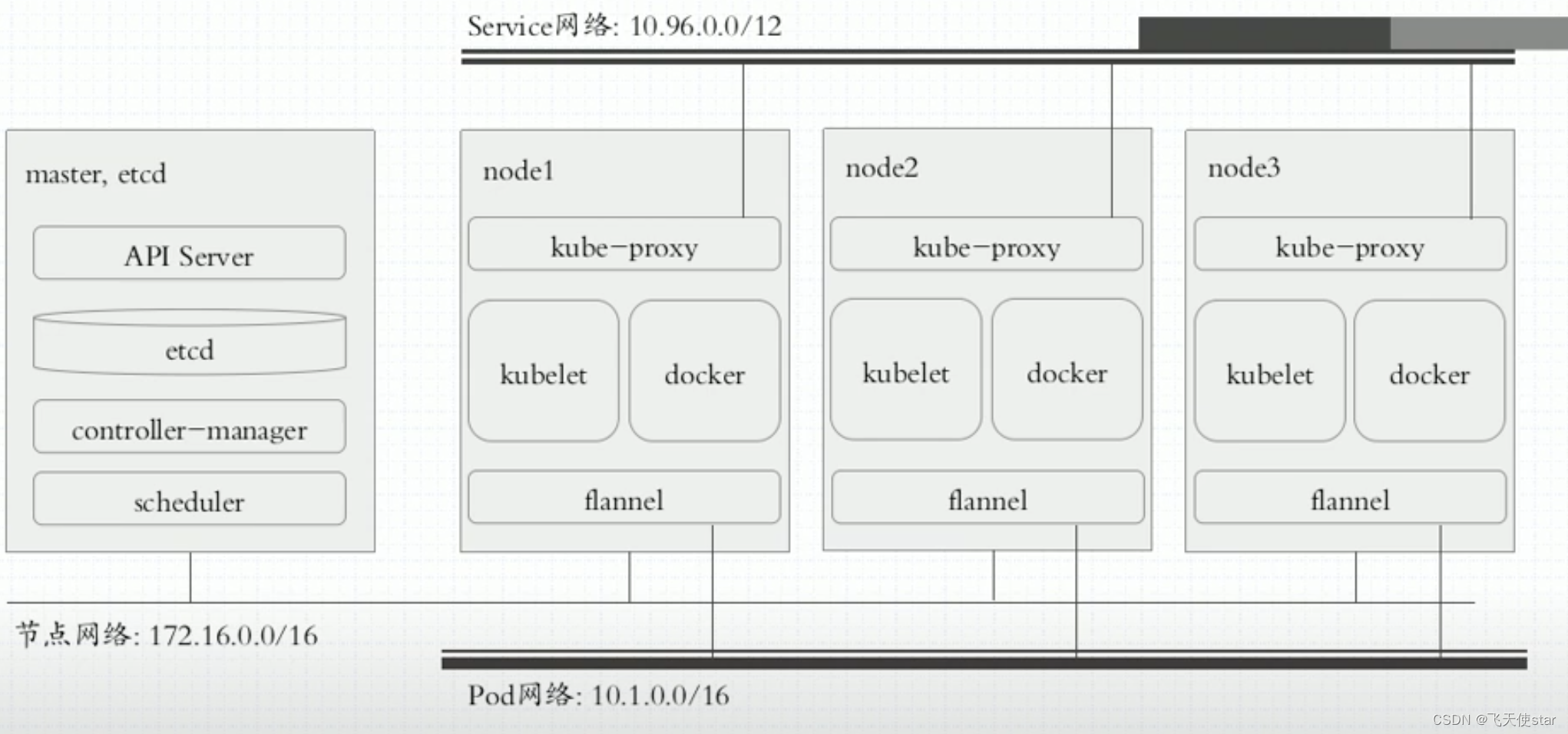
飞天使-k8s知识点1-kubernetes架构简述
文章目录 名词功能要点 k8s核心要素CNCF 云原生框架简介k8s组建介绍 名词 CI 持续集成, 自动化构建和测试:通过使用自动化构建工具和自动化测试套件,持续集成可以帮助开发人员自动构建和测试他们的代码。这样可以快速检测到潜在的问题,并及早…...
linux中deadline调度原理与代码注释
简介 deadline调度是比rt调度更高优先级的调度,它没有依赖于优先级的概念,而是给了每个实时任务一定的调度时间,这样的好处是:使多个实时任务场景的时间分配更合理,不让一些实时任务因为优先级低而饿死。deadline调度…...

jquery、vue、uni-app、小程序的页面传参方式
jQuery、Vue、Uni-app 和小程序(例如微信小程序)都有它们自己的页面传参方式。下面分别介绍这几种方式的页面传参方式: jQuery: 在jQuery中,页面传参通常是通过URL的查询参数来实现的。例如: <a href"page2…...
ModuleNotFoundError: No module named ‘openai.error‘
ModuleNotFoundError: No module named ‘openai.error’ result self.fn(*self.args, **self.kwargs) File “H:\chatGPTWeb\chatgpt-on-wechat\channel\chat_channel.py”, line 168, in _handle reply self._generate_reply(context) File “H:\chatGPTWeb\chatgpt-on-wec…...

理解pom.xml中的parent标签
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: 循序渐进学SpringBoot ✨特色专栏&…...
element ui el-avatar 源码解析零基础逐行解析
avatar功能介绍 快捷配置头像的样式 avatar 的参数配置 属性说明参数size尺寸type string 类型 (‘large’,‘medium’,‘small’)number类型 validator 校验shape形状circle (原型) square(方形)icon传入的iconsrc传入的图片st…...
Linux下c语言实现动态库的动态调用
在Linux操作系统下,有时候需要在不重新编译程序的情况下,运行时动态地加载库,这时可以通过Linux操作系统提供的API可以实现,涉及到的API主要有dlopen、dlsym和dlclose。使用时,需要加上头文件#include <dlfcn.h>…...
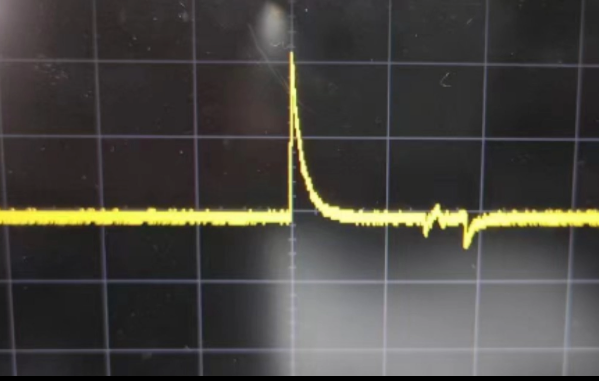
为什么MCU在ADC采样时IO口有毛刺?
大家在使用MCU内部ADC进行信号采样一个静态电压时,可能在IO口上看到这样的波形。这个时候大家一般会认识是信号源有问题,但仔细观察会发现这个毛刺的频率是和ADC触发频率一样的。 那么为什么MCU在ADC采样时IO口会出现毛刺呢?这个毛刺对结果有…...

C# 将 Word 转化分享为电子期刊
目录 需求 方案分析 相关库引入 关键代码 Word 转 Pdf Pdf 转批量 Jpeg Jpeg 转为电子书 实现效果演示 小结 需求 曾经的一个项目,要求实现制作电子期刊定期发送给企业进行阅读,基本的需求如下: 1、由编辑人员使用 Microsoft Word…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
