LA@线性代数学习总结@主要对象和问题@思想方法
文章目录
- 线性代数研究对象
- 主要问题
- 联系
- 核心概念
- 核心定理
- 核心操作和运算
- 基础
- 高级
- 小结
- 性质和推导方法
- 问题转换为线性方程组求解问题
- 验证和推导性质定理
线性代数研究对象
- 线性代数的研究对象主要是行列式和矩阵(向量)
- 矩阵这种对象可以做的操作和运算很多,特别是方阵,它们的计算量天然就有较大的特点,
- 例如:伴随矩阵的计算,矩阵乘法,计算逆矩阵等,其中又以矩阵乘法运算最为重要,几乎贯穿整个学科的始终,是许多其他概念和计算的基础
主要问题
为了解决几个重要问题,提出了许多概念,例如秩,初等变换和基于这些概念的方法
- 矩阵方程和线性方程组的解
- 向量组的线性相关性
- 特征值和特征向量问题
- 矩阵(方阵)相似对角化问题
- 二次型问题
联系
-
向量组线性相关问题和特征值和特征向量问题,本质上可以转化为线性方程组的解的问题
-
例如向量组 A A A线性相关用线性方程组描述为 A x = 0 \bold{Ax=0} Ax=0
(1)存在非零解,这又等价于 R ( A ) < n R(A)<n R(A)<n问题(其中 n n n为 x \bold{x} x的维数,或向量组 A A A包含的向量个数) -
向量组 B B B能够由 A A A线性表出,则 A X = B \bold{AX=B} AX=B
(2)有解 -
矩阵 A \bold{A} A关于特征值 λ \lambda λ的特征向量 A α = λ α \bold{A\alpha=\lambda\alpha} Aα=λα
(3)求解,可以转换为线性方程组 ( λ E − A ) α = 0 (\lambda\bold{E}-A)\alpha=\bold{0} (λE−A)α=0(3-1)或 ( A − λ E ) α = 0 (\bold{A}-\lambda\bold{E})\alpha=0 (A−λE)α=0(3-2)有求非零解问题(方程(3,3-1,3-2)是等价方程)- 其中行列式 ∣ λ E − A ∣ |\lambda\bold{E}-\bold{A}| ∣λE−A∣
(4)是方阵 A \bold{A} A的特征多项式,根据Cramer法则,方程(3-1)具有非零解的条件是(4)取 0 0 0 - 由此可以求出所有特征值
- 再分别求出矩阵 A \bold{A} A的属于每个特征值的特征向量,也就是求线性方程组 λ E − A = 0 \lambda{\bold{E}}-\bold{A}=\bold{0} λE−A=0的解
- 其中行列式 ∣ λ E − A ∣ |\lambda\bold{E}-\bold{A}| ∣λE−A∣
-
特征值和特征向量为矩阵相似对角化可行性的判定作铺垫,矩阵 A A A的 k i k_i ki重特征值 λ i \lambda_{i} λi具有 k i k_i ki个线性无关特征向量时,矩阵 A A A可以对角化
-
二次型 f ( x 1 , ⋯ , x n ) f(x_1,\cdots,x_{n}) f(x1,⋯,xn)= x T A x \bold{x^{T}Ax} xTAx的问题,本质上二次型的对称阵 A \bold{A} A问题
-
二次型标准化问题对应于 A \bold{A} A的相似对角化问题
-
对称阵 A \bold{A} A一定可以相似对角化,而且是正交相似对角化,
-
一定存在正交阵 Q \bold{Q} Q( Q T = Q − 1 \bold{Q^{T}=Q^{-1}} QT=Q−1)使得 Q T A Q \bold{Q^{T}AQ} QTAQ= Q − 1 A Q \bold{Q^{-1}AQ} Q−1AQ= Λ \Lambda Λ
-
或者说 A \bold{A} A相似且合同于某个对角阵 Λ \Lambda Λ= d i a g ( λ 1 , ⋯ , λ n ) \mathrm{diag}(\lambda_1,\cdots,\lambda_n) diag(λ1,⋯,λn),其中 λ 1 , ⋯ , λ n \lambda_1,\cdots,\lambda_{n} λ1,⋯,λn是 A \bold{A} A的特征值)
-
-
二次型规范化问题:任何二次型都可以规范化
-
二次型(对应矩阵)正定问题
-
-
核心概念
-
基本概念:
- 行列式
- 矩阵
- 线性方程组
-
抽象概念
- 矩阵的秩
- 向量组的秩
核心定理
-
线性方程组有解判定定理及其推广
- A x = b \bold{Ax=b} Ax=b
- A X = B \bold{AX=B} AX=B
- 判定条件: R ( A ) = R ( A , B ) R(\bold{A})=R(\bold{A,B}) R(A)=R(A,B)
-
向量组线性相关性判定定理
- 本质上是线性方程组的应用,将向量组线性相关性问题通过建立对应的线性方程组,转化为分析方程组解的情况问题
- 向量组线性相关有许多结论,这些结论很多都可以用本定理推导证明
-
秩的相关定理
- 由于线性方程组判定定理涉及到秩,因此关于秩相关定理和常用
- 例如
- 矩阵作初等行变换不改变秩
- R ( A ) ⩽ R ( A , B ) R(\bold{A})\leqslant{R(\bold{A,B})} R(A)⩽R(A,B)(或部分组的秩不超过整体组的秩)
核心操作和运算
基础
- 转置运算
- 内积运算
- 矩阵乘法运算
- 初等变换运算
- 向量单位化运算
高级
- 方阵行列式运算
- 矩阵(向量组)秩
- 求逆运算
- 对角化
小结
- 矩阵乘法和初等变换是最核心的矩阵操作
性质和推导方法
问题转换为线性方程组求解问题
- 大多数问题都可以和线性方程组的求解问题挂钩,通过构造线性方程组来研究线性代数的大多数问题
- 而线性方程组的解由依赖矩阵乘法和矩阵的秩
- 矩阵乘法负责问题表达和转换
- 而系数矩阵和增广矩阵的秩的判定直接决定了线性方程组解的情况
- 而矩阵的秩又依赖于初等变换
- 可见初等变换和矩阵乘法的重要性
- 而线性方程组的解由依赖矩阵乘法和矩阵的秩
验证和推导性质定理
- 线性代数中有很多利用运用构造法,化归法,反证法的例子
-
例如证明 R ( A + B ) ⩽ R ( A ) + R ( B ) R(A+B)\leqslant{R(A)+R(B)} R(A+B)⩽R(A)+R(B)的过程中,我们可以构造 ( A + B B ) \begin{pmatrix}A+B\\B\end{pmatrix} (A+BB),再利用更加基础的结论证明它:
- ( A + B B ) \begin{pmatrix}A+B\\B\end{pmatrix} (A+BB), ( A B ) \begin{pmatrix}A\\B\end{pmatrix} (AB)有相同的秩
- R ( A ) , R ( B ) R(A),R(B) R(A),R(B) ⩽ \leqslant ⩽ R ( A B ) R\begin{pmatrix}A\\B\end{pmatrix} R(AB) ⩽ \leqslant ⩽ R ( A ) + R ( B ) R(A)+R(B) R(A)+R(B)
- 换元代入完成证明
-
构造齐次线性方程组 A x = 0 \bold{Ax=0} Ax=0,通过研究其解的情况来研究向量组 A A A的线性相关性
-
反证法:许多关于存在性的命题和结论可以用反证法证明,例如线性相关性命题
-
相关文章:

LA@线性代数学习总结@主要对象和问题@思想方法
文章目录 线性代数研究对象主要问题联系核心概念核心定理 核心操作和运算基础高级小结 性质和推导方法问题转换为线性方程组求解问题验证和推导性质定理 线性代数研究对象 线性代数的研究对象主要是行列式和矩阵(向量)矩阵这种对象可以做的操作和运算很多,特别是方阵,它们的计…...
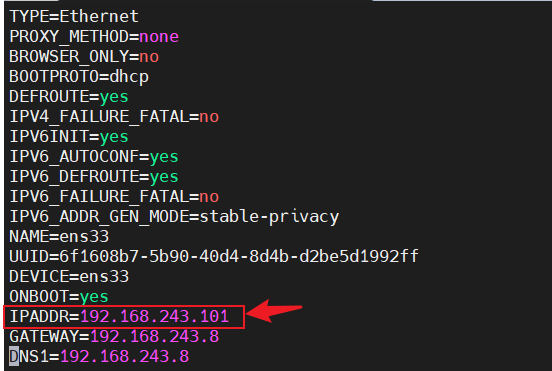
VMware克隆虚拟机
要求:利用模板虚拟机hadoop100,克隆出hadoop101虚拟机。 1、鼠标右键点击已存在的模板虚拟机hadoop100 --> 管理 --> 克隆 2、选择克隆自虚拟机中的当前状态 3、创建完整克隆 4、修改虚拟机名称、位置 5、等待克隆完成后,则成功克隆出…...

C语言中常见的关键字
一、数据类型关键字(20个) 基本数据类型(5个) void:声明函数无返回值或无参数,声明无类型指针,显式丢弃运算结果 char:字符型类型数据,属于整型数据的一种 intÿ…...
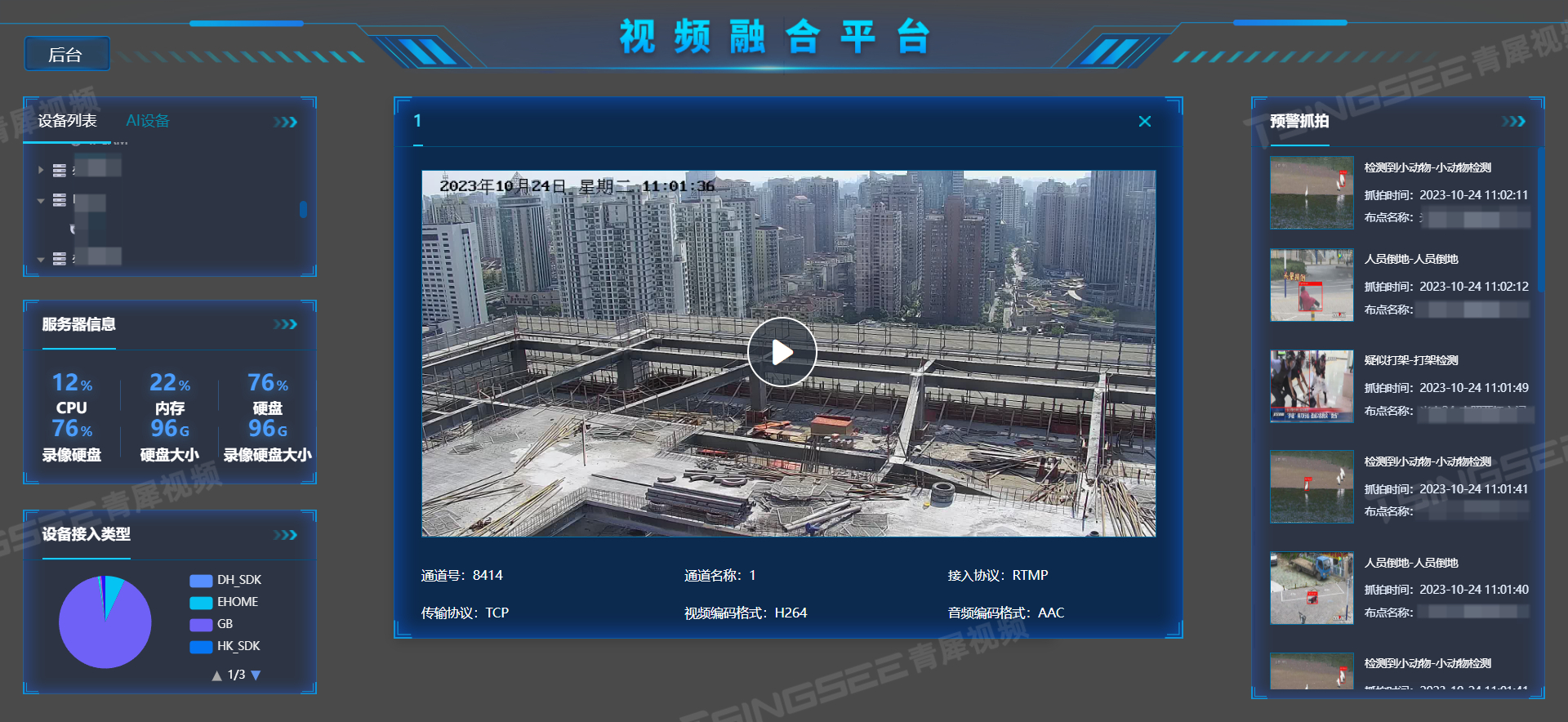
新型智慧视频监控系统:基于TSINGSEE青犀边缘计算AI视频识别技术的应用
边缘计算AI智能识别技术在视频监控领域的应用有很多。这项技术结合了边缘计算和人工智能技术,通过在摄像头或网关设备上运行AI算法,可以在现场实时处理和分析视频数据,从而实现智能识别和分析。目前来说,边缘计算AI视频智能技术可…...

智能优化算法应用:基于梯度算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于梯度算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于梯度算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.梯度算法4.实验参数设定5.算法结果6.参考文献7.MA…...
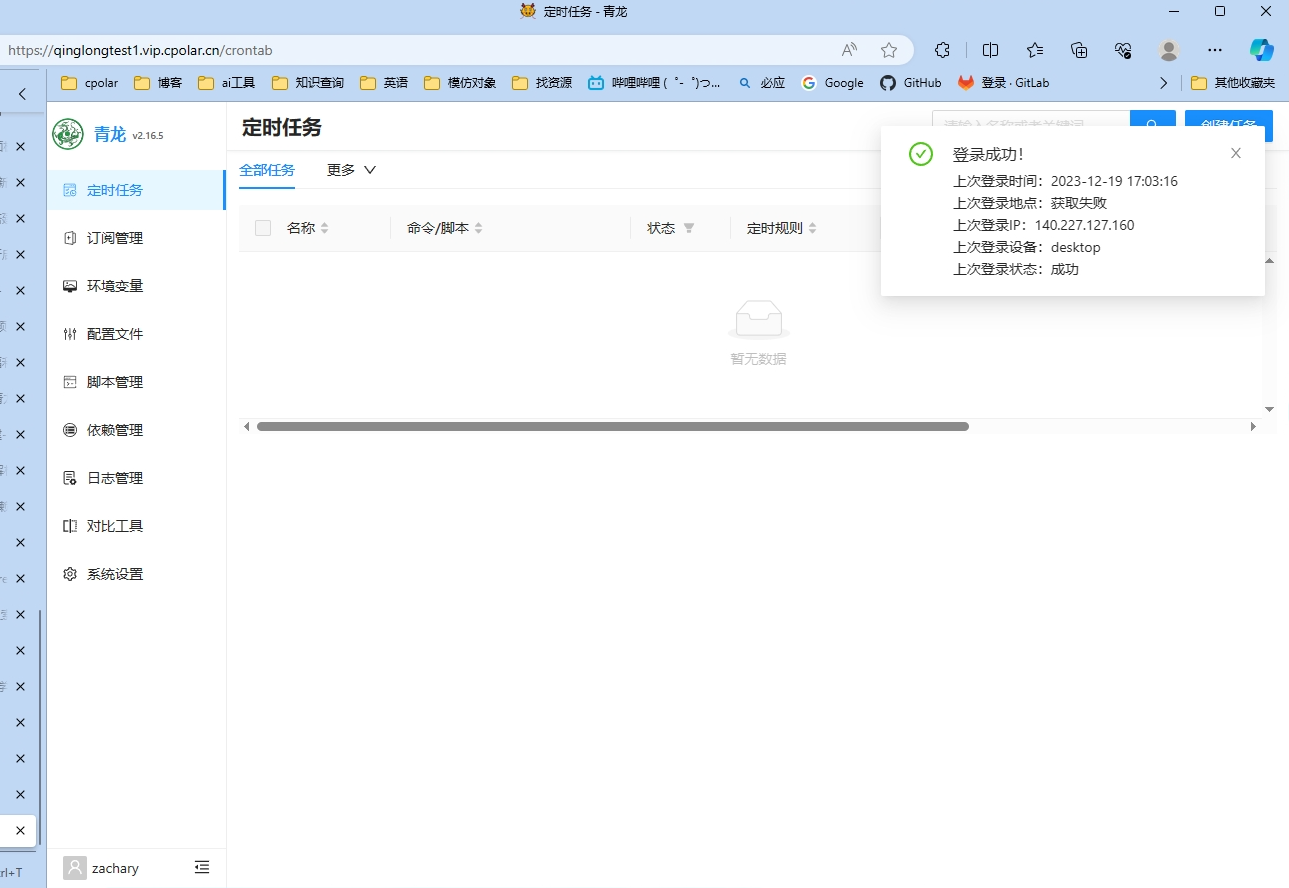
如何使用Docker搭建青龙面板并结合内网穿透工具发布至公网可访问
文章目录 一、前期准备本教程环境为:Centos7,可以跑Docker的系统都可以使用。本教程使用Docker部署青龙,如何安装Docker详见: 二、安装青龙面板三、映射本地部署的青龙面板至公网四、使用固定公网地址访问本地部署的青龙面板 正文…...
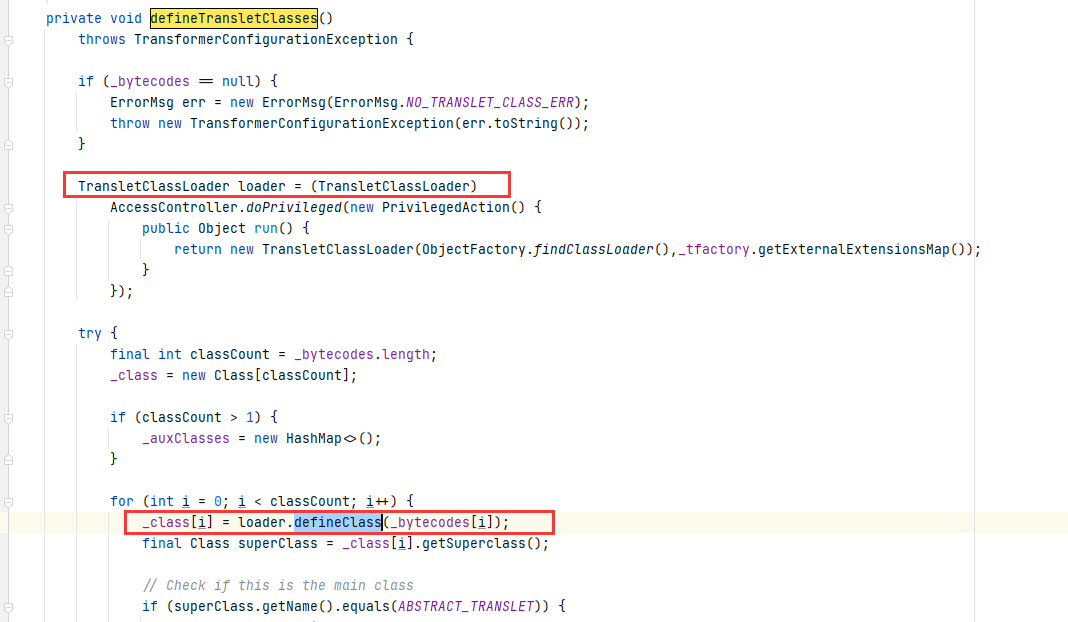
fastjson1.2.24 反序列化漏洞(CVE-2017-18349)分析
FastJson在< 1.2.24 版本中存在反序列化漏洞,主要原因FastJson支持的两个特性: fastjson反序列化时,JSON字符串中的type字段,用来表明指定反序列化的目标恶意对象类。fastjson反序列化时,字符串时会自动调用恶意对…...

Linux中history使用(过滤,显示时间,查找)
显示历史命令 history 显示最后几条执行命令 history 5 显示history记录中命令执行时间 export HISTTIMEFORMAT"%F %T " 显示命令中有某些内容的最后几条执行命令 history | grep key | tail -n 2...
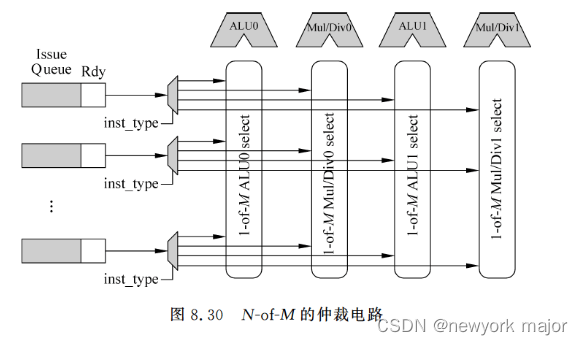
issue阶段的选择电路的实现
1-of-M的仲裁电路 为什么要实现oldest-first 功能的仲裁呢? 这是考虑到越是旧的指令,和它存在相关性的指令也就越多,因此优先执行最旧的指令,则可以唤醒更多的指令,能够有效地提高处理器执行指令的并行度,而且最旧的指…...
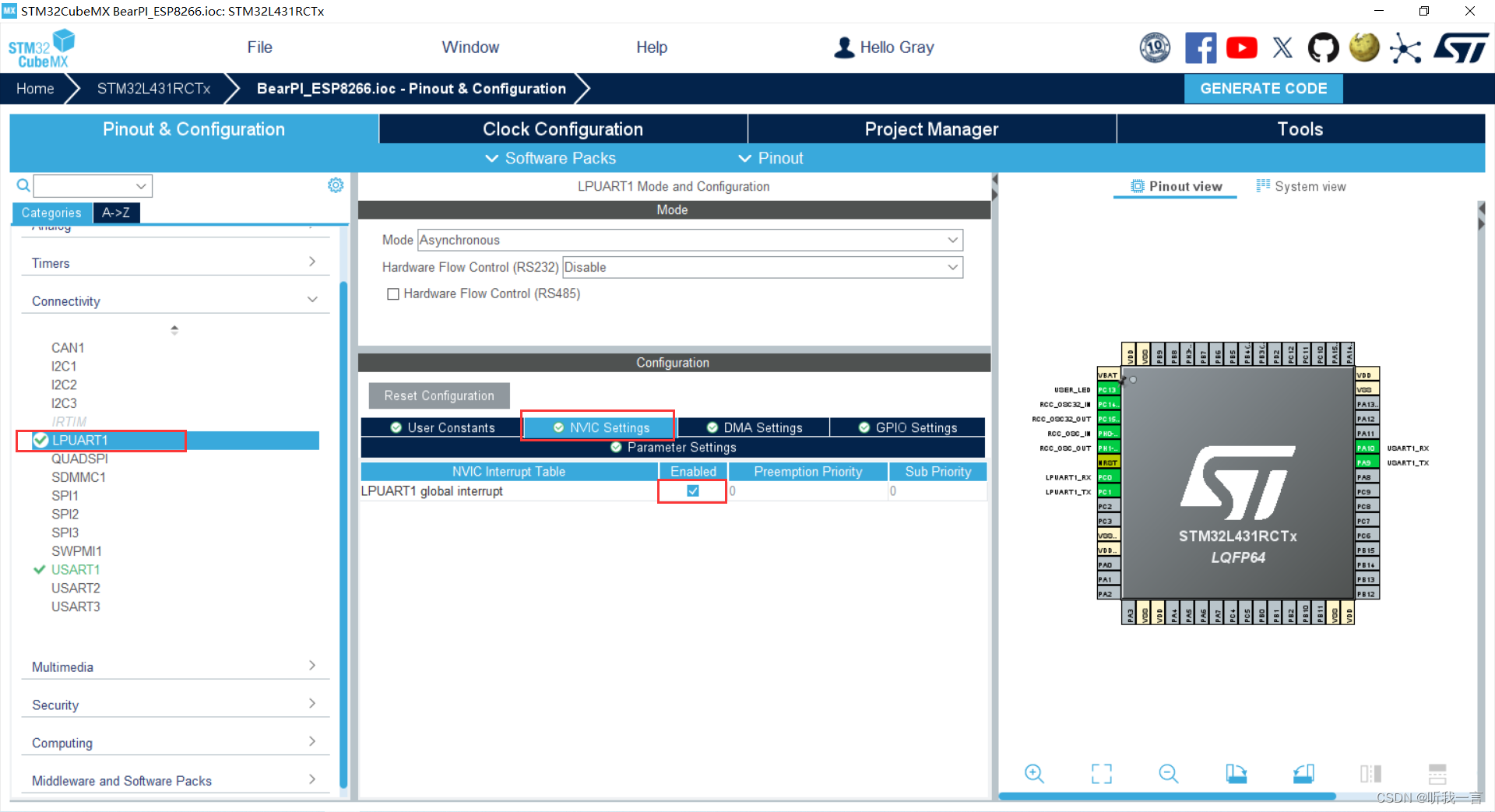
BearPi Std 板从入门到放弃 - 后天篇(3)(ESP8266透传点灯)
简介 电脑搭建一个TCP Server, ESP8266 串口设置好透传模式, 再由TCP Server发送指令控制灯的亮灭; 开灯指令: led_on回车 ; 关灯指令: led_off回车 主芯片: STM32L431RCT6 LED : PC13 \ 推挽输出即可 \ 高电平点亮 串口: Usart1 / LPUART E…...

【Linux】macOS下使用scp命令编写脚本上传文件至服务器
使用时需要输入服务器密码 #!/bin/bash# 检查传递给脚本的参数数量 if [ "$#" -ne 2 ]; thenecho "Usage: $0 <本地文件路径> <服务器文件夹路径>"exit 1 fi# 接收命令行参数 local_file"$1" remote_path"$2"# 定义远程服…...

难以置信:WINDOWS11真的取消了助记符
助记符是个好东西,记住了非常的方便。这几天升级到WINDOWS11之后,发现助记符被全面取消!真是难以置信! 现在WIN11越来越象MAC,MAC好用吗?当然不好用。 其实WIN11完全可以开发两套界面,各取所需。…...
使用VSC从零开始Vue.js——备赛笔记——2024全国职业院校技能大赛“大数据应用开发”赛项——任务3:数据可视化
使用Visual Studio Code(VSC)进行Vue开发非常方便,下面是一些基本步骤: 一、下载和安装Vue 官网下载地址Download | Node.js Vue.js是基于Node.js的,所以首先需要安装Node.js,官网下载地址:No…...

企业直聘招聘人才求职系统招聘会小程序系统源码
技术栈: 端 原生小程序开发 后端php7.2 数据库mysql5.6 主要功能: 企业入住 ,企业直聘 个人实名认证,人才求职 发布线上招聘会 企业招聘邀请 个人简历置顶 刷新 浏览足迹浏览 附近 招聘信息查看...
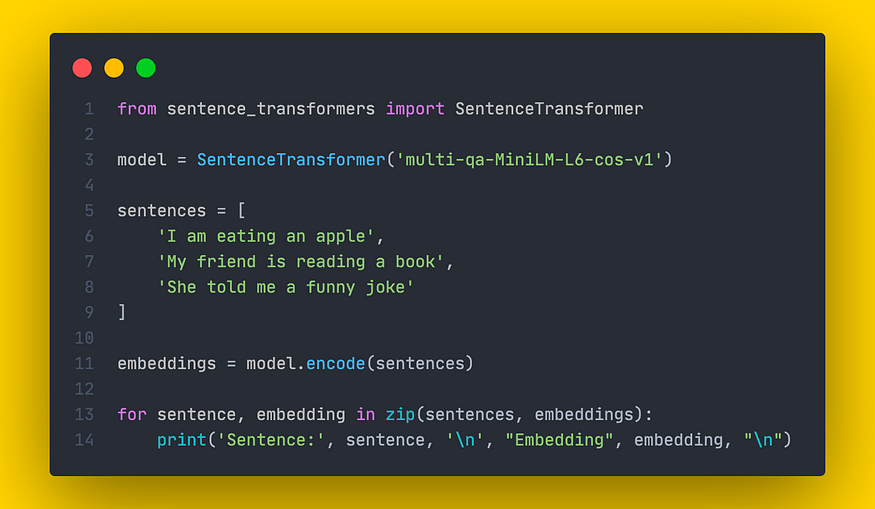
大型语言模型:SBERT — Sentence-BERT
slavahead 一、介绍 Transformer 在 NLP 方面取得了进化进步,这已经不是什么秘密了。基于转换器,许多其他机器学习模型已经发展起来。其中之一是BERT,它主要由几个堆叠的变压器编码器组成。除了用于情感分析或问答等一系列不同的问题外&#…...

高效编写软件测试报告的关键技巧
引言: 软件测试报告是测试团队与开发团队之间沟通的重要工具,它记录了测试过程中的发现、问题和建议。一个清晰、准确、高效的软件测试报告可以帮助开发团队更好地理解测试结果,并及时修复问题。本文将介绍一些高效编写软件测试报告的关键技巧…...

编写CI/CD自动化部署脚本
编写CI/CD自动化部署脚本 什么是CI/CD CI/CD 是现代软件开发过程中的关键实践,它包含两个缩写: CI,或者持续集成(Continuous Integration)CD,可以指持续交付(Continuous Delivery)…...

Pandas实践_分类数据
文章目录 一、cat对象1.cat对象的属性2.类别的增加、删除和修改 二、有序分类1.序的建立2.排序和比较 三、区间类别1.利用cut和qcut进行区间构造2.一般区间的构造3.区间的属性与方法 一、cat对象 1.cat对象的属性 在pandas中提供了category类型,使用户能够处理分类…...
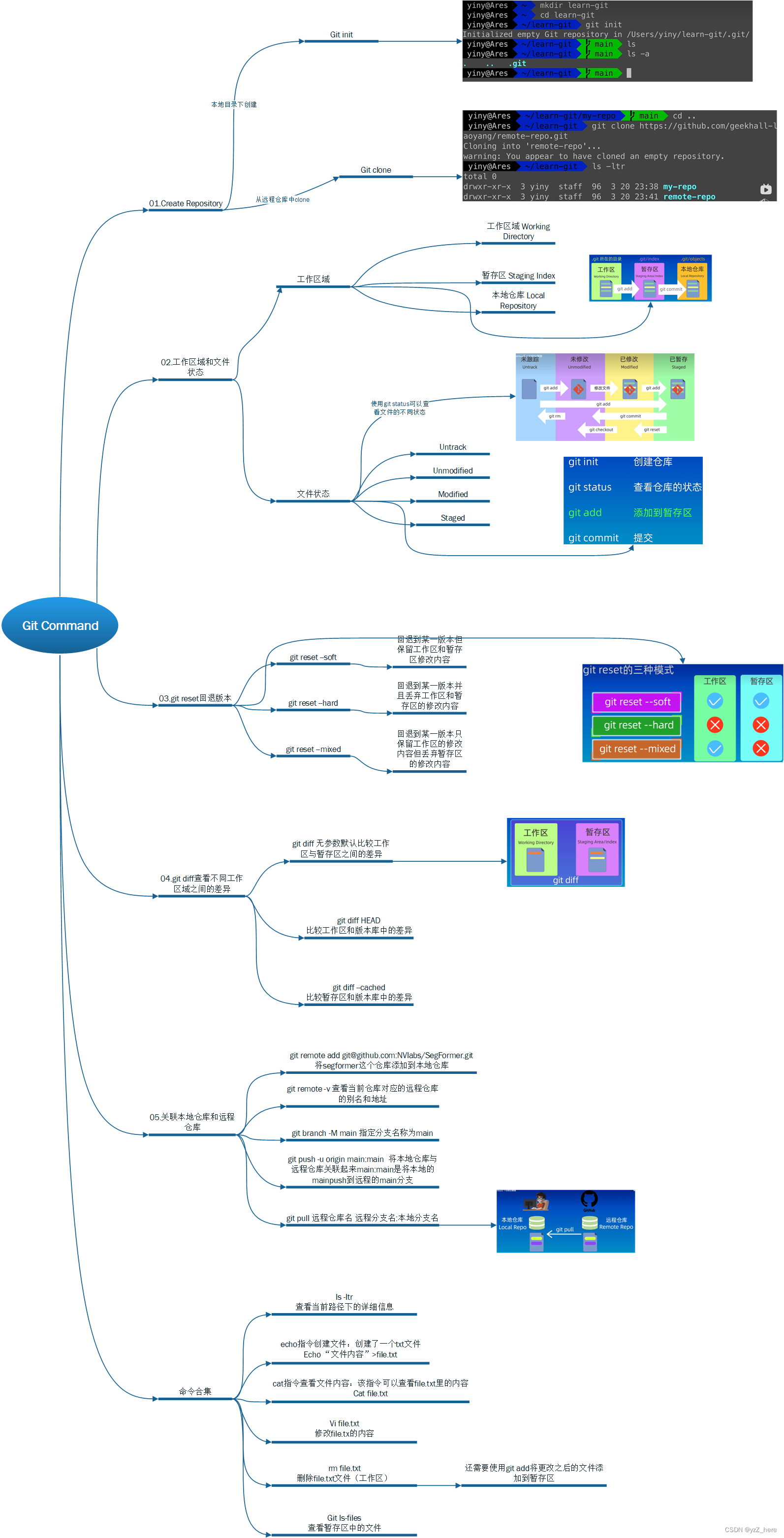
git的使用思维导图
源文件在github主页:study_collection/cpp学习/git at main stu-yzZ/study_collection (github.com)...

Qt 软件界面点击QCombBox控件,造成整个界面移位
Qt 软件界面点击QCombBox控件,造成整个界面移位 最近项目中,遇到了一个问题,在绘制界面的时候,使用了QCombBox控件,在点击QCombBox控件下拉中的item时,会造成整个界面移位的现象。 我重写了下面三个事件函…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
