图像卷积操作
目录
一、互相关运算
二、卷积层
三、图像中目标的边缘检测
四、学习卷积核
五、特征映射和感受野
一、互相关运算
严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation),而不是卷积运算。在卷积层中,输入张量和核张量通过互相关运算产生输出张量。
首先,我们暂时忽略通道(第三维)这一情况,看看如何处理二维图像数据和隐藏表示。在 下图中,输入是高度为 、宽度为
的二维张量(即形状为
)。卷积核的高度和宽度都是
,而卷积核窗口(或卷积窗口)的形状由内核的高度和宽度决定(即
)。

在二维互相关运算中,卷积窗口从输入张量的左上角开始,从左到右、从上到下滑动。当卷积窗口滑动到新一个位置时,包含在该窗口中的部分张量与卷积核张量进行按元素相乘,得到的张量再求和得到一个单一的标量值,由此我们得出了这一位置的输出张量值。
在如上例子中,输出张量的四个元素由二维互相关运算得到,这个输出高度为 、宽度为
,如下所示:
注意,输出大小略小于输入大小。这是因为卷积核的宽度和高度大于1,而卷积核只与图像中每个大小完全适合的位置进行互相关运算。所以,输出大小等于输入大小 减去卷积核大小
加
,即:
接下来,我们在`corr2d`函数中实现如上过程,该函数接受输入张量`X`和卷积核张量`K`,并返回输出张量`Y`。
import torch
from torch import nn
from d2l import torch as d2ldef corr2d(X, K):"""计算二维互相关运算"""h, w = K.shapeY = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1)) # 先算出输出张量的形状并初始化为0for i in range(Y.shape[0]):for j in range(Y.shape[1]):Y[i, j] = (X[i:i + h, j:j + w] * K).sum() # 输出张量的每一个元素都是X与K经过某种计算得到的return Y # 返回二维互相关运算后的结果Y我们来验证上述二维互相关运算的输出。
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(corr2d(X, K))tensor([[19., 25.],[37., 43.]])二、卷积层
卷积层对输入和卷积核权重进行互相关运算,并在添加标量偏置之后产生输出。所以,卷积层中的两个被训练的参数是卷积核权重和标量偏置,如下图所示。就像我们之前随机初始化全连接层一样,在训练基于卷积层的模型时,我们也随机初始化卷积核权重。

基于上面定义的`corr2d`函数实现二维卷积层。在`__init__`构造函数中,将`weight`和`bias`声明为两个模型参数。前向传播函数调用`corr2d`函数并添加偏置。
class Conv2D(nn.Module):def __init__(self, kernel_size):super().__init__()self.weight = nn.Parameter(torch.rand(kernel_size))self.bias = nn.Parameter(torch.zeros(1))def forward(self, x):return corr2d(x, self.weight) + self.bias 高度和宽度分别为 和
的卷积核可以被称为
卷积或
卷积核。我们也将带有
卷积核的卷积层称为
卷积层。
三、图像中目标的边缘检测
如下是卷积层的一个简单应用:通过找到像素变化的位置,来检测图像中不同颜色的边缘。
首先,我们构造一个 像素的黑白图像。中间四列为黑色(
),其余像素为白色(
)。
X = torch.ones((6, 8))
X[:, 2:6] = 0
print(X)tensor([[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.],[1., 1., 0., 0., 0., 0., 1., 1.]]) 接下来,我们构造一个高度为 、宽度为
的卷积核`K`。当进行互相关运算时,如果水平相邻的两元素相同,则输出为零,否则输出为非零。
K = torch.tensor([[1.0, -1.0]])现在,我们对参数`X`(输入)和`K`(卷积核)执行互相关运算。如下所示,输出`Y`中的1代表从白色到黑色的边缘,-1代表从黑色到白色的边缘,其他情况的输出为0。
Y = corr2d(X, K)
Ytensor([[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.],[ 0., 1., 0., 0., 0., -1., 0.]])现在我们将输入的二维图像转置,再进行如上的互相关运算。其输出如下,之前检测到的垂直边缘消失了。不出所料,这个卷积核`K`只可以检测垂直边缘,无法检测水平边缘。
corr2d(X.t(), K)tensor([[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.],[0., 0., 0., 0., 0.]])四、学习卷积核
如果我们只需寻找黑白边缘,那么以上`[1, -1]`的边缘检测器足以。然而,当有了更复杂数值的卷积核,或者连续的卷积层时,我们不可能手动设计滤波器。那么我们可以学习由`X`生成`Y`的卷积核。
现在让我们看看是否可以通过仅查看“输入-输出”对来学习由`X`生成`Y`的卷积核。我们先构造一个卷积层,并将其卷积核初始化为随机张量。接下来,在每次迭代中,我们比较`Y`与卷积层输出的平方误差,然后计算梯度来更新卷积核。为了简单起见,我们在此使用内置的二维卷积层,并忽略偏置。
# 构造一个二维卷积层,它具有1个输入通道、1个输出通道和形状为(1,2)的卷积核
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False) # 因为我们前面用的是二维互相关运算corr2d()由X生成的Y,因此不需要bias# 这个二维卷积层使用四维输入和输出格式(批量大小、通道、高度、宽度),
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
lr = 3e-2 # 学习率for i in range(10):Y_hat = conv2d(X)l = (Y_hat - Y) ** 2 # 使用均方误差conv2d.zero_grad()l.sum().backward()# 迭代卷积核conv2d.weight.data[:] -= lr * conv2d.weight.grad # 手写实现梯度下降if (i + 1) % 2 == 0:print(f'epoch {i+1}, loss {l.sum():.3f}')epoch 2, loss 6.422
epoch 4, loss 1.225
epoch 6, loss 0.266
epoch 8, loss 0.070
epoch 10, loss 0.022在10次迭代之后,误差已经降到足够低。现在我们来看看我们所学的卷积核的权重张量。
conv2d.weight.data.reshape((1, 2))tensor([[ 1.0010, -0.9739]])我们学习到的卷积核权重非常接近我们之前定义的卷积核`K`。
五、特征映射和感受野
下图中输出的卷积层有时被称为特征映射(feature map),因为它可以被视为一个输入映射到下一层的空间维度的转换器。

在卷积神经网络中,对于某一层的任意元素 ,其感受野(receptive field)是指在前向传播期间可能影响
计算的所有元素(来自所有先前层)。
请注意,感受野可能大于输入的实际大小。让我们用上图为例来解释感受野:给定 卷积核,阴影输出元素值
的感受野是输入阴影部分的四个元素。假设之前输出为
,其大小为
,现在我们在其后附加一个卷积层,该卷积层以
为输入,输出单个元素
。在这种情况下,
上的
的感受野包括
的所有四个元素,而输入的感受野包括最初所有九个输入元素。
因此,当一个特征图中的任意元素需要检测更广区域的输入特征时,我们可以构建一个更深的网络。
相关文章:
图像卷积操作
目录 一、互相关运算 二、卷积层 三、图像中目标的边缘检测 四、学习卷积核 五、特征映射和感受野 一、互相关运算 严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation),而不是…...
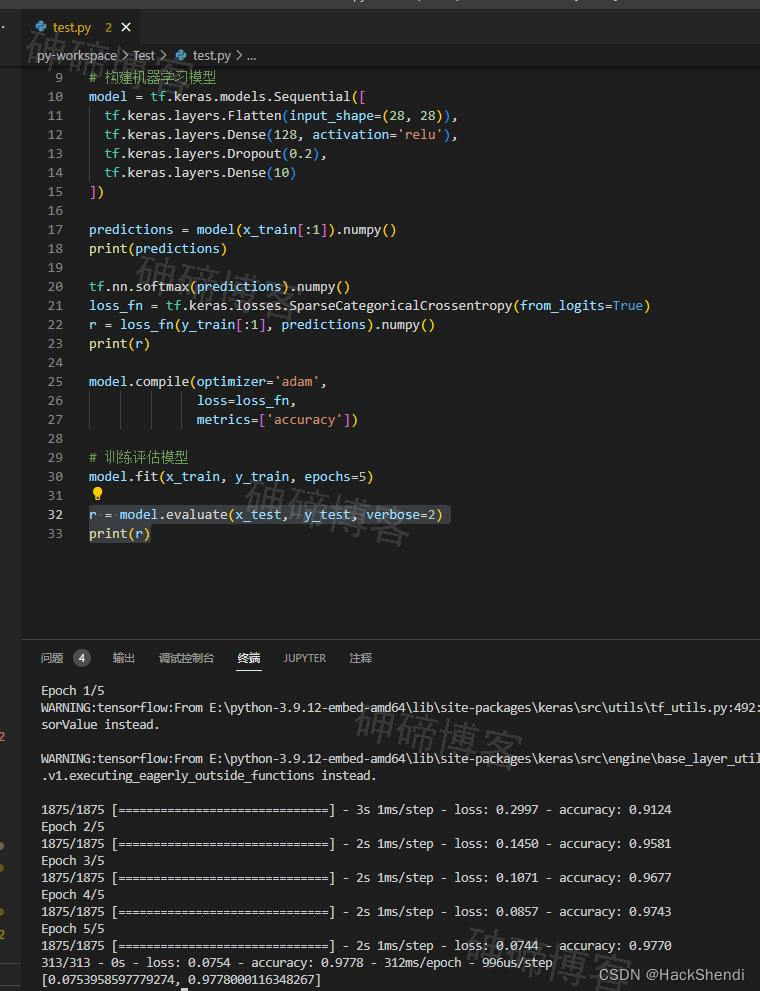
目标检测入门体验,技术选型,加载数据集、构建机器学习模型、训练并评估
Hi, I’m Shendi 1、目标检测入门体验,技术选型,加载数据集、构建机器学习模型、训练并评估 在最近有了个物体识别的需求,于是开始学习 在一番比较与询问后,最终选择 TensorFlow。 对于编程语言,我比较偏向Java或nod…...

【UE5插件推荐】运行时,通过HTTP / HTTPS下载文件(Runtime Files Downloader)
UE5 github Home gtreshchev/RuntimeFilesDownloader Wiki (github.com)...
信息论安全与概率论
目录 一. Markov不等式 二. 选择引理 三. Chebyshev不等式 四. Chernov上限 4.1 变量大于 4.2 变量小于 信息论安全中会用到很多概率论相关的上界,本文章将梳理几个论文中常用的定理,重点关注如何理解这些定理以及怎么用。 一. Markov不等式 假定…...
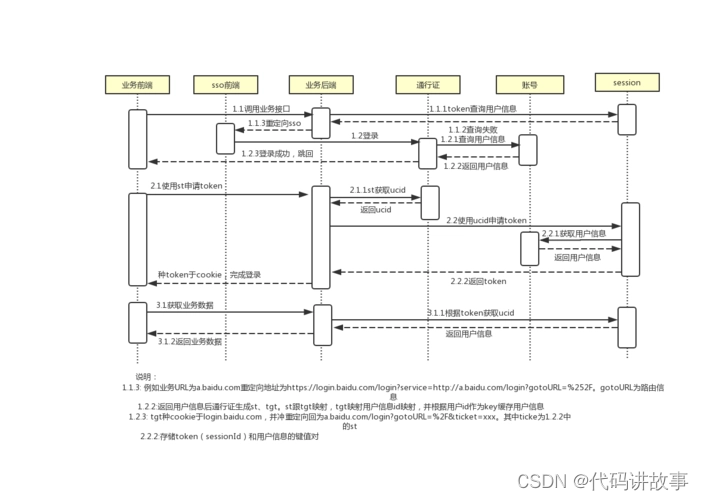
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统。 单点登录(SSO)是一个登录服务层,通过一次登录访问多个应用。使用SSO服务可以提高多系统使用的用户体验和安全性,用户不必记忆多个密…...

Netty Review - 优化Netty通信:如何应对粘包和拆包挑战
文章目录 概述Pre概述场景复现解决办法概览方式一: 特殊分隔符分包 (演示Netty提供的众多方案中的一种)流程分析 方式二: 发送长度(推荐) DelimiterBasedFrameDecoder 源码分析 概述 Pre Netty Review - 借助SimpleTalkRoom初体验…...

vue介绍以及基本指令
目录 一、vue是什么 二、使用vue的准备工作 三、创建vue项目 四、vue插值表达式 五、vue基本指令 六、key的作用 七、v-model 九、指令修饰符 一、vue是什么 Vue是一种用于构建用户界面的JavaScript框架。它可以帮助开发人员构建单页应用程序和复杂的前端应用程序。Vue…...

重塑数字生产力体系,生成式AI将开启云计算未来新十年?
科技云报道原创。 今天我们正身处一个历史的洪流,一个巨变的十字路口。生成式AI让人工智能技术完全破圈,带来了机器学习被大规模采用的历史转折点。 它掀起的新一轮科技革命,远超出我们今天的想象,这意味着一个巨大的历史机遇正…...

JFreeChart 生成图表,并为图表标注特殊点、添加文本标识框
一、项目场景: Java使用JFreeChart库生成图片,主要场景为将具体的数据 可视化 生成曲线图等的图表。 本篇文章主要针对为数据集生成的图表添加特殊点及其标识框。具体包括两种场景:x轴为 时间戳 类型和普通 数值 类型。(y轴都为…...

vue整合axios 未完
一、简介 1、介绍 axios前端异步请求库类似jouery ajax技术,axios用来在前端页面发起一个异步请求,请求之后页面不动,响应回来刷新页面局部;Axios 是一个基于 promise 的 HTTP 库,可以用在浏览器和 node.js 中 2、特…...

java代码编写twitter授权登录
在上一篇内容已经介绍了怎么申请twitter开放的API接口。 下面介绍怎么通过twitter提供的API,进行授权登录功能。 开发者页面设置 首先在开发者页面开启“用户认证设置”,点击edit进行信息编辑。 我的授权登录是个网页,并且只需要进行简单的…...
SK Ecoplant借助亚马逊云科技,海外服务器为环保事业注入新活力
在当今全球面临着资源紧缺和环境挑战的大背景下,数字技术所依赖的海外服务器正成为加速循环经济转型的关键利器。然而,很多企业在整合数字技术到运营中仍然面临着一系列挑战,依然存在低效流程导致的不必要浪费。针对这一问题,SK E…...
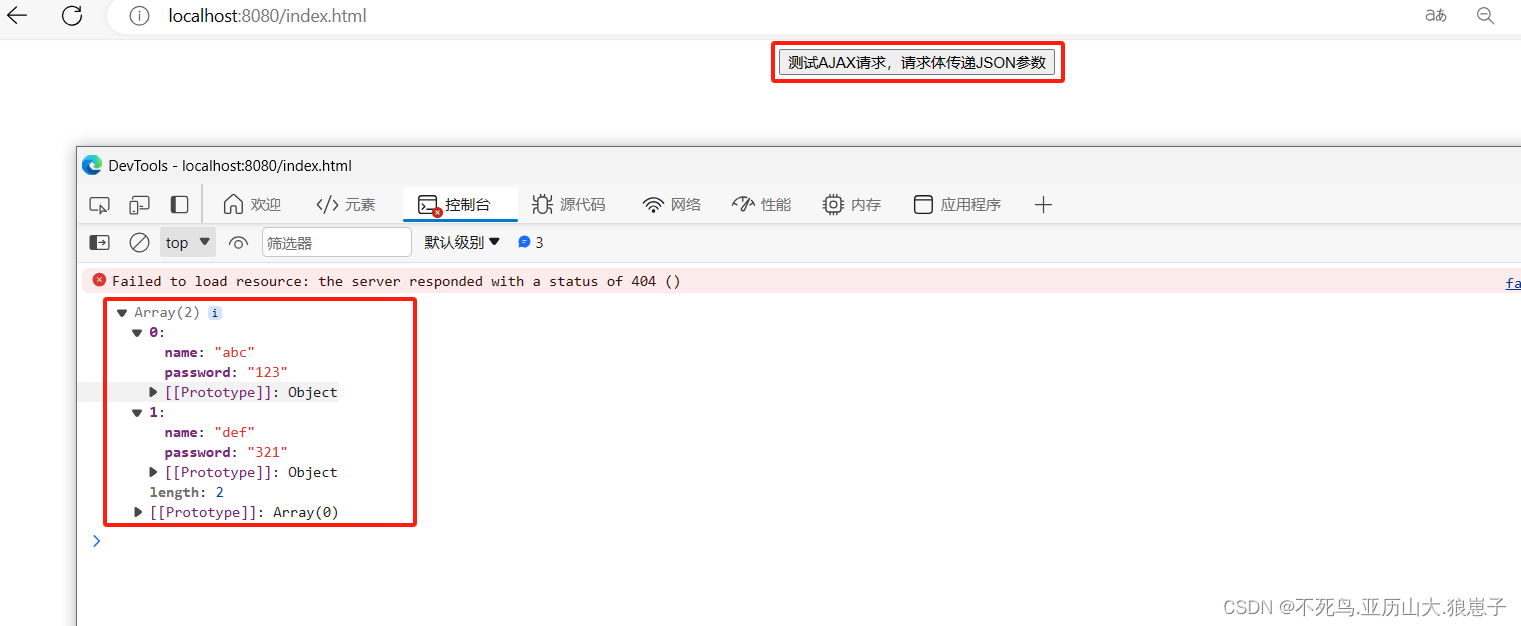
RPC(5):AJAX跨域请求处理
接上一篇RPC(4):HttpClient实现RPC之POST请求进行修改。 1 修改客户端项目 1.1 修改maven文件 修改后配置文件如下: <dependencyManagement><dependencies><dependency><groupId>org.springframework.b…...

用大白话举例子讲明白区块链
什么是区块链?网上这么说: 区块链是一种分布式数据库技术,它以块的形式记录和存储交易数据,并使用密码学算法保证数据的安全性和不可篡改性。每个块都包含了前一个块的哈希值和自身的交易数据,形成了一个不断增长的链条…...

Java URL
URL:统一资源定位符,说白了,就是一个网络 通过URLConnection类可以连接到URL,然后通过URLConnection可以获取读数据的通道。非文本数据用字节流来读取。 读完之后写入本地即可。 public class test {public static void main(S…...
:ETL涉及到的名词解释)
ETL-从1学到100(1/100):ETL涉及到的名词解释
本文章主要介绍ETL和大数据中涉及到名词,同时解释这些名词的含义。由于不是一次性收集这些名词,所以这篇文章将会持续更新,更新日志会存放在本段话下面: 12-19更新:OLTP、OLAP、BI、ETL。 12-20更新:ELT、…...

Jenkins + gitlab 持续集成和持续部署的学习笔记
1. Jenkins 介绍 软件开发生命周期(SLDC, Software Development Life Cycle):它集合了计划、开发、测试、部署的集合。 软件开发瀑布模型 软件的敏捷开发 1.1 持续集成 持续集成 (Continuous integration 简称 CI): 指的是频繁的将代码集成到主干。 持续集成的流…...

R语言【cli】——通过cli_abort用 cli 格式的内容显示错误、警告或信息,内部调用cli_bullets和inline-makeup
cli_abort(message,...,call .envir,.envir parent.frame(),.frame .envir ) 先从那些不需要下大力气理解的参数入手: 参数【.envir】:进行万能表达式编译的环境。 参数【.frame】:抛出上下文。默认用于参数【.trace_bottom】ÿ…...

cka从入门到放弃
无数次想放弃,最后选择了坚持 监控pod日志 监控名为 foobar 的 Pod 的日志,并过滤出具有 unable-access-website 信息的行,然后将 写入到 /opt/KUTR00101/foobar # 解析 监控pod的日志,使用kubectl logs pod-name kubectl logs…...

通过 jekyll 构建 github pages 博客实战笔记
jekyll 搭建教程 jekyll 搭建教程 Gem 安装 Ruby,请访问 下载地址。 Jekyll Jekyll 是一个简单且具备博客特性的静态网站生成器。 Jekyll 中文文档 极客学院中文文档 使用以下命令安装 Jekyll。 $ gem install jekyll在中国可能需要使用代理软件。然后ÿ…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...
