DDPM推导笔记
各位佬看文章之前,可以先去看看这个视频,并给这位up主点赞投币,这位佬讲解的太好了:大白话AI
1.前置知识的学习
1.1 正态分布特性
(1)正态分布的概率密度函数
f ( x ) = 1 2 π σ e − ( x − μ ) 2 2 σ 2 , 记为 N ( μ , σ 2 ) f(x) = {1 \over \sqrt{2 \pi } \sigma} e^{-{{(x-\mu)^2} \over {2 \sigma^2}}} ,记为N(\mu, \sigma^2) f(x)=2πσ1e−2σ2(x−μ)2,记为N(μ,σ2)
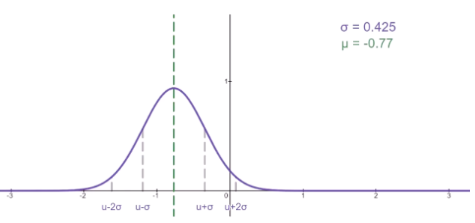
当 μ = 0 , σ 2 = 1 \mu = 0, \sigma^2=1 μ=0,σ2=1时,则记为标准正态分布,记为 N ( 0 , 1 ) N(0, 1) N(0,1), 又称为高斯分布。
(2)正态分布的基本性质
N ( μ 1 , σ 1 2 ) + N ( μ 2 , σ 2 2 ) = N ( μ 1 + μ 2 , σ 1 2 + σ 2 2 ) a ∗ N ( μ , σ ) = N ( a ∗ μ , ( a ∗ σ ) 2 ) N(\mu_1, \sigma_1^2) + N(\mu_2, \sigma_2^2) = N(\mu_1+\mu2, \sigma_1^2+\sigma_2^2) \\ a*N(\mu, \sigma) = N(a*\mu, (a*\sigma)^2) N(μ1,σ12)+N(μ2,σ22)=N(μ1+μ2,σ12+σ22)a∗N(μ,σ)=N(a∗μ,(a∗σ)2)
1.2 贝叶斯定理
A , B A, B A,B是两个随机事件, P ( A ) P(A) P(A)表示 事件 A 事件A 事件A发生的概率, P ( B ∣ A ) P(B|A) P(B∣A)表示A事件发生的情况下B事件发生的概率,则贝叶斯定理如下:
P ( A ∣ B ) = P ( B ∣ A ) ∗ P ( A ) P ( B ) P(A|B) = {{P(B|A) * P(A)} \over P(B)} P(A∣B)=P(B)P(B∣A)∗P(A)
2. 前向过程(加噪)

如图所示,前向过程则是一个加载过程,在每个时间步,都从正态分布中随机采样一个和图片等大的噪声(也可以理解为噪声图片),则加噪过程:
x 1 = β 1 ∗ ϵ 1 + 1 − β 1 ∗ x 0 x_1 = \sqrt{\beta_1} * \epsilon_1 + \sqrt{1-\beta_1} * x_0 x1=β1∗ϵ1+1−β1∗x0
其中 x 0 x_0 x0表示原始图片, ϵ 1 \epsilon_1 ϵ1 表示随机噪声, β 1 \beta_1 β1表示扩散速度, T T T表示扩散的次数,则可以一次推导:
x 1 = β 1 ∗ ϵ 1 + 1 − β 1 ∗ x 0 x 2 = β 2 ∗ ϵ 2 + 1 − β 2 ∗ x 1 x 3 = β 3 ∗ ϵ 3 + 1 − β 3 ∗ x 2 ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ x T = β T ∗ ϵ T + 1 − β T ∗ x T − 1 前后关系就可以记为: x t = β t ∗ ϵ t + 1 − β t ∗ x t − 1 x_1 = \sqrt{\beta_1} * \epsilon_1 + \sqrt{1-\beta_1} * x_0 \\ x_2 = \sqrt{\beta_2} * \epsilon_2 + \sqrt{1-\beta_2} * x_1 \\ x_3 = \sqrt{\beta_3} * \epsilon_3 + \sqrt{1-\beta_3} * x_2 \\ ······ \\ x_T = \sqrt{\beta_T} * \epsilon_T + \sqrt{1-\beta_T} * x_{T-1} \\ 前后关系就可以记为: \\ x_t = \sqrt{\beta_t} * \epsilon_t + \sqrt{1-\beta_t} * x_{t-1} \\ x1=β1∗ϵ1+1−β1∗x0x2=β2∗ϵ2+1−β2∗x1x3=β3∗ϵ3+1−β3∗x2⋅⋅⋅⋅⋅⋅xT=βT∗ϵT+1−βT∗xT−1前后关系就可以记为:xt=βt∗ϵt+1−βt∗xt−1
为简化后续运算,令 α t = 1 − β t \alpha_t = 1 - \beta_t αt=1−βt, 则有:
x t = 1 − α t ∗ ϵ t + α t ∗ x t − 1 x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * x_{t-1} xt=1−αt∗ϵt+αt∗xt−1
思考:如何能更快的得到 x T x_T xT?因为如果加噪1000步,岂不是要计算1000次上述的运算!好的,下面介绍怎样依赖正态分布的可加性来简化运算,从而推导出 x 0 x_0 x0到 x t x_t xt的关系:
由: x t = 1 − α t ∗ ϵ t + α t ∗ x t − 1 x t − 1 = 1 − α t − 1 ∗ ϵ t − 1 + α t − 1 ∗ x t − 2 把 x t − 1 代入到 x t 中可以推导出: x t = 1 − α t ∗ ϵ t + α t ∗ ( 1 − α t − 1 ∗ ϵ t − 1 + α t − 1 ∗ x t − 2 ) = a t ( 1 − a t − 1 ) ∗ ϵ t − 1 + 1 − a t ∗ ϵ t + a t a t − 1 ∗ x t − 2 其中: ϵ t − 1 和 ϵ t 是两个随机噪声,且两者是两个独立的随机变量。 打个比喻:我们有一个骰子掷两次分别得到 ϵ t − 1 和 ϵ t ,完全可以等效 于我们有两个骰子掷一次。即:一个骰子掷两次的概率分布等同于两个骰子掷一次的概率分布,所以 , 如果我们知道两个骰子掷一次的概率分布,然后进行一次采样即可。 由: \\ x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * x_{t-1} \\ x_{t-1} = \sqrt{1- \alpha_{t-1}} * \epsilon_{t-1} + \sqrt{\alpha_{t-1}} * x_{t-2} \\ 把x_{t-1}代入到x_t中可以推导出: \\ x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * (\sqrt{1- \alpha_{t-1}} * \epsilon_{t-1} + \sqrt{\alpha_{t-1}} * x_{t-2}) \\ = \sqrt{a_t(1-a_{t-1})} * \epsilon_{t-1} + \sqrt{1-a_t} * \epsilon_t + \sqrt{a_t a_{t-1}} * x_{t-2} \\ 其中:\epsilon_{t-1} 和 \epsilon_{t} 是两个随机噪声,且两者是两个独立的随机变量。\\ 打个比喻:我们有一个骰子掷两次分别得到\epsilon_{t-1} 和 \epsilon_{t},完全可以等效\\ 于我们有两个骰子掷一次。即:一个骰子掷两次的概率分布等同于两个骰子掷一次的概率分布,所以,\\ 如果我们知道两个骰子掷一次的概率分布,然后进行一次采样即可。 \\ 由:xt=1−αt∗ϵt+αt∗xt−1xt−1=1−αt−1∗ϵt−1+αt−1∗xt−2把xt−1代入到xt中可以推导出:xt=1−αt∗ϵt+αt∗(1−αt−1∗ϵt−1+αt−1∗xt−2)=at(1−at−1)∗ϵt−1+1−at∗ϵt+atat−1∗xt−2其中:ϵt−1和ϵt是两个随机噪声,且两者是两个独立的随机变量。打个比喻:我们有一个骰子掷两次分别得到ϵt−1和ϵt,完全可以等效于我们有两个骰子掷一次。即:一个骰子掷两次的概率分布等同于两个骰子掷一次的概率分布,所以,如果我们知道两个骰子掷一次的概率分布,然后进行一次采样即可。
由正态分布的基本性质可知: ϵ t 和 ϵ t − 1 服从 N ( 0 , 1 ) , 即: ϵ t ∼ N ( 0 , 1 ) , ϵ t − 1 ∼ N ( 0 , 1 ) 可以推导出: 1 − a t ∗ ϵ t ∼ N ( 0 , 1 − α t ) a t ( 1 − a t − 1 ) ∗ ϵ t − 1 ∼ N ( 0 , a t − a t ∗ a t − 1 ) ) 由正态分布的基本性质可知:\\ \epsilon_t和\epsilon_{t-1}服从N(0, 1),即:\epsilon_t \sim N(0,1), \epsilon_{t-1} \sim N(0,1) \\ 可以推导出: \sqrt{1-a_t} * \epsilon_t \sim N(0, 1- \alpha_t) \\ \sqrt{a_t(1-a_{t-1})} * \epsilon_{t-1} \sim N(0, a_t-a_t*a_{t-1})) 由正态分布的基本性质可知:ϵt和ϵt−1服从N(0,1),即:ϵt∼N(0,1),ϵt−1∼N(0,1)可以推导出:1−at∗ϵt∼N(0,1−αt)at(1−at−1)∗ϵt−1∼N(0,at−at∗at−1))
从而推导出: a t ( 1 − a t − 1 ) ∗ ϵ t − 1 + 1 − a t ∗ ϵ t ∼ N ( 0 , 1 − a t ∗ a t − 1 ) 从而推导出: \\ \sqrt{a_t(1-a_{t-1})} * \epsilon_{t-1} + \sqrt{1-a_t} * \epsilon_t \sim N(0, 1-a_t*a_{t-1}) 从而推导出:at(1−at−1)∗ϵt−1+1−at∗ϵt∼N(0,1−at∗at−1)
进而推导出: x t = 1 − a t ∗ a t − 1 ∗ ϵ + a t ∗ a t − 1 ∗ x t − 2 , 其中: ϵ ∼ N ( 0 , 1 − a t ∗ a t − 1 ) 进而推导出:\\ x_t = \sqrt{1-a_t*a_{t-1}} * \epsilon + \sqrt{a_t*a_{t-1}}*x_{t-2}, 其中:\epsilon \sim N(0, 1-a_t*a_{t-1}) 进而推导出:xt=1−at∗at−1∗ϵ+at∗at−1∗xt−2,其中:ϵ∼N(0,1−at∗at−1)
这里就可到了 x t 和 x t − 2 之间的关系,然后依靠上面的方法就可以一次推导出 x t 到 x 0 的关系 ( 数学归纳法证明 ) ,具体如下: x t = 1 − a t a t − 1 a t − 2 . . . a 1 ∗ ϵ + a t a t − 1 a t − 2 . . . a 1 ∗ x 0 其中, ϵ ∼ N ( 0 , 1 − a t a t − 1 a t − 2 . . . a 1 ) 这里就可到了x_t和x_{t-2}之间的关系,然后依靠上面的方法就可以一次推导出x_t到x_0的关系(数学归纳法证明),具体如下: \\ x_t = \sqrt{1 - a_ta_{t-1}a_{t-2}...a_1} * \epsilon + \sqrt{a_ta_{t-1}a_{t-2}...a1} * x_0 \\ 其中,\epsilon \sim N(0, 1 - a_ta_{t-1}a_{t-2}...a_1) 这里就可到了xt和xt−2之间的关系,然后依靠上面的方法就可以一次推导出xt到x0的关系(数学归纳法证明),具体如下:xt=1−atat−1at−2...a1∗ϵ+atat−1at−2...a1∗x0其中,ϵ∼N(0,1−atat−1at−2...a1)
为了方便表示 , 记: a ˉ t = a t a t − 1 a t − 2 . . . a 1 则: x t = 1 − a ˉ t ∗ ϵ + a ˉ t x 0 为了方便表示,记: \bar{a}_t = a_ta_{t-1}a_{t-2}...a_1 \\ 则: x_t = \sqrt{1 - \bar{a}_t} * \epsilon + \sqrt{\bar{a}_t} x_0 为了方便表示,记:aˉt=atat−1at−2...a1则:xt=1−aˉt∗ϵ+aˉtx0
至此,前向过程就记录完成了,我们得到 x 0 到 x t x_0到x_t x0到xt的关系,并且可以只通过一次采样就能得到。
3. 反向过程(去噪)
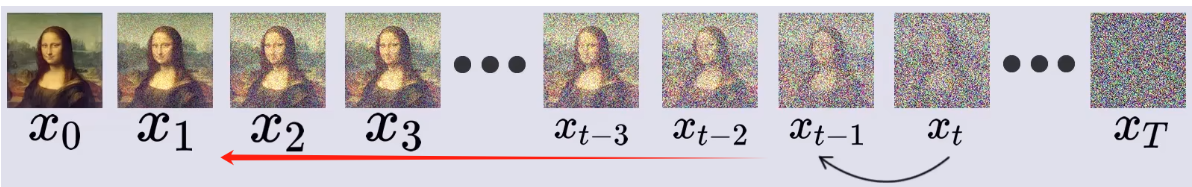
去噪过程就是从 x T x_T xT一步步反推回 x 0 x_0 x0。
3.1 反向原理推导
由贝叶斯定理:
P ( A ∣ B ) = P ( B ∣ A ) ∗ P ( A ) P ( B ) P(A|B) = {{P(B|A) * P(A)} \over P(B)} P(A∣B)=P(B)P(B∣A)∗P(A)
我们可以令:
由于 x t 到 x t − 1 是一个随机过程,则令: P ( x t − 1 ∣ x t ) : 表示在给定 x t 的情况下, x t − 1 的概率。 套用贝叶斯定理得: P ( x t − 1 ∣ x t ) = P ( x t ∣ x t − 1 ) ∗ P ( x t − 1 ) P ( x t ) 其中, P ( x t ) 和 P ( x t − 1 ) 分别表示 x t 和 t t − 1 的概率 , 也就是从 x 0 原图得到它们的概率。 由于x_t到x_{t-1}是一个随机过程,则令: \\ P(x_{t-1}|x_t): 表示在给定x_t的情况下,x_{t-1}的概率。 \\ 套用贝叶斯定理得: \\ P(x_{t-1} | x_t) = { P(x_t | x_{t-1}) * P(x_{t-1}) \over P(x_t)} \\ 其中,P(x_t)和P(x_{t-1})分别表示x_t和t_{t-1}的概率,也就是从x_0原图得到它们的概率。 由于xt到xt−1是一个随机过程,则令:P(xt−1∣xt):表示在给定xt的情况下,xt−1的概率。套用贝叶斯定理得:P(xt−1∣xt)=P(xt)P(xt∣xt−1)∗P(xt−1)其中,P(xt)和P(xt−1)分别表示xt和tt−1的概率,也就是从x0原图得到它们的概率。
所以,可以在每个式子后面添加一个先验 x 0 , 即: P ( x t − 1 ∣ x t , x 0 ) = P ( x t ∣ x t − 1 , x 0 ) ∗ P ( x t − 1 ∣ x 0 ) P ( x t ∣ x 0 ) 所以,可以在每个式子后面添加一个先验x0,即: \\ P(x_{t-1} | x_t,x_0) = { P(x_t | x_{t-1},x_0) * P(x_{t-1} | x_0) \over P(x_t | x_0)} \\ 所以,可以在每个式子后面添加一个先验x0,即:P(xt−1∣xt,x0)=P(xt∣x0)P(xt∣xt−1,x0)∗P(xt−1∣x0)
有: P ( x t ∣ x t − 1 , x 0 ) 给定 x t − 1 到 x t 的概率。 前向过程中可知: x t = 1 − α t ∗ ϵ t + α t ∗ x t − 1 x t = 1 − a ˉ t ∗ ϵ + a ˉ t x 0 ϵ t 和 ϵ 分别服从 N ( 0 , 1 ) 从而推导出: x t ∼ N ( a t x t − 1 , 1 − a t ) 或: x t ∼ N ( a ˉ t x 0 , 1 − a ˉ t ) 以及: x t − 1 ∼ N ( a ˉ t − 1 x 0 , 1 − a ˉ t − 1 ) 有: \\ P(x_t|x_{t-1}, x_0) 给定x_{t-1}到x_t的概率。 \\ 前向过程中可知: \\ x_t = \sqrt{1- \alpha_t} * \epsilon_t + \sqrt{\alpha_t} * x_{t-1} \\ x_t = \sqrt{1 - \bar{a}_t} * \epsilon + \sqrt{\bar{a}_t} x_0 \\ \epsilon_t和\epsilon分别服从N(0, 1) \\ 从而推导出: \\ x_t \sim N(\sqrt{a_t} x_{t-1}, 1-a_t) \\ 或: \\ x_t \sim N(\sqrt{\bar{a}_t} x_0, 1-\bar{a}_t) \\ 以及: \\ x_{t-1} \sim N(\sqrt{\bar{a}_{t-1}} x_0, 1-\bar{a}_{t-1}) \\ 有:P(xt∣xt−1,x0)给定xt−1到xt的概率。前向过程中可知:xt=1−αt∗ϵt+αt∗xt−1xt=1−aˉt∗ϵ+aˉtx0ϵt和ϵ分别服从N(0,1)从而推导出:xt∼N(atxt−1,1−at)或:xt∼N(aˉtx0,1−aˉt)以及:xt−1∼N(aˉt−1x0,1−aˉt−1)
然后就可以把他们分别写成概率密度形式:

然后将概率密度函数带入到贝叶斯定理中,就可以得到:

化简成高斯分布得:
P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0) =

由此推导出:
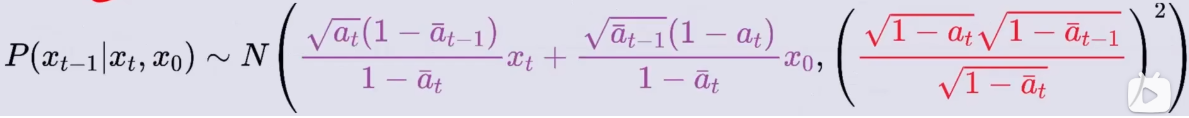
我们的目的是通过 x t 求出 x t − 1 , 然后由 x t − 1 推导出 x t − 2 ⋅ ⋅ ⋅ 直到求出 x 0 , 但现在的式子中出现了 x 0 , 怎么办? 没关系,我们之前由 x t 和 x 0 的关系: x t = 1 − a ˉ t ∗ ϵ + a ˉ t x 0 我们的目的是通过x_t求出x_{t-1},然后由x_{t-1}推导出x_{t-2}···直到求出x_0,\\ 但现在的式子中出现了x_0,怎么办? \\ 没关系,我们之前由x_t和x_0的关系: \\ x_t = \sqrt{1 - \bar{a}_t} * \epsilon + \sqrt{\bar{a}_t} x_0 \\ 我们的目的是通过xt求出xt−1,然后由xt−1推导出xt−2⋅⋅⋅直到求出x0,但现在的式子中出现了x0,怎么办?没关系,我们之前由xt和x0的关系:xt=1−aˉt∗ϵ+aˉtx0
变换可以得到:

将它带入到 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)的概率密度函数中可得:
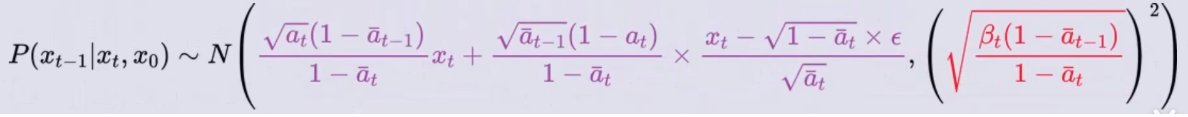
它表示的是:对于任意 x t x_t xt的图像都可以用 x 0 x_0 x0加载而来;而只要知道了从 x 0 x_0 x0到 x t x_t xt加入的噪声 ϵ \epsilon ϵ,就能得到它前一时刻 x t − 1 x_{t-1} xt−1的概率分布,即: P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0) 。
这里我们就需要使用神经网络,输入 x t x_t xt时刻的图像,预测此图像相对于某个 x 0 x_0 x0原图加入的噪声 ϵ \epsilon ϵ。
如图所示,也就是说:
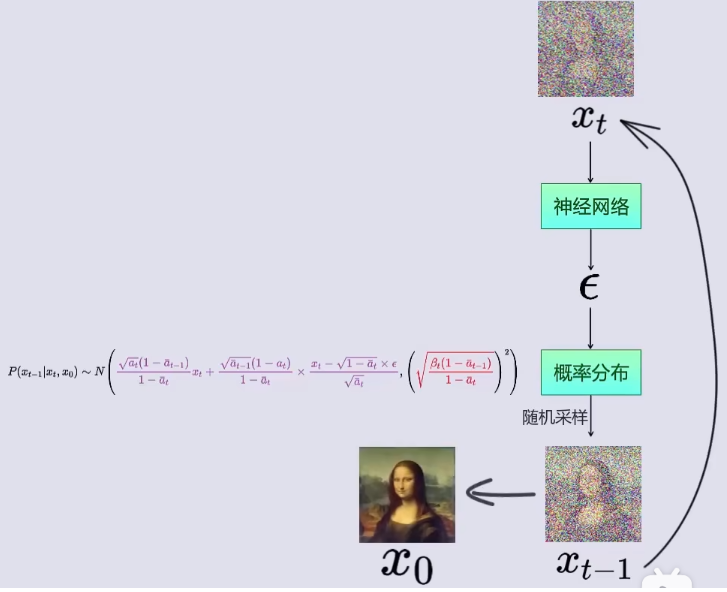
Step1: 在神经网络中,输入 x t x_t xt时刻图像,训练得到此图像相对于某个 x 0 x_0 x0原图加入的噪声 ϵ \epsilon ϵ。
Step2: 将噪声 ϵ \epsilon ϵ带入到 x t − 1 x_{t-1} xt−1的概率密度函数 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)中;
Step3: 从 x t − 1 x_{t-1} xt−1的概率密度函数 P ( x t − 1 ∣ x t , x 0 ) P(x_{t-1}|x_t, x_0) P(xt−1∣xt,x0)中随机采样,得到 x t − 1 x_{t-1} xt−1(即t-1时刻对应的图像);
Step4: 将 x t − 1 x_{t-1} xt−1作为神经网络的输入,带入到Step1中,循环Step1 ~ Step3,知道得到 x 0 x_0 x0
DDPM中的神经网络选用的UNet.
至此,结束!
相关文章:

DDPM推导笔记
各位佬看文章之前,可以先去看看这个视频,并给这位up主点赞投币,这位佬讲解的太好了:大白话AI 1.前置知识的学习 1.1 正态分布特性 (1)正态分布的概率密度函数 f ( x ) 1 2 π σ e − ( x − μ ) …...

【C#/Java】【小白必看】不要只会读写文本文件了!对象序列化助你提高效率
【C#/Java】【小白必看】不要只会读写文本文件了!对象序列化助你提高效率 在编程的世界里,文件的读写操作是我们经常面对的任务之一。 当我们只涉及简单的文本文件时,这个任务似乎并不复杂。但是,当我们处理更为复杂的类对…...
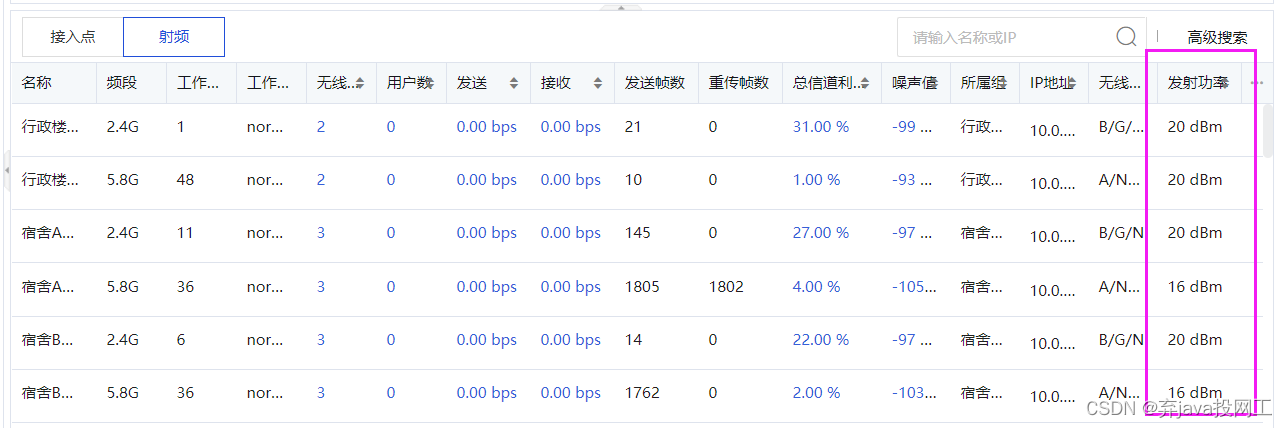
排障启示录-无线终端信号弱
现象:无线终端显示信号弱 信息收集: AP的实际发射功率低。外置天线型AP,天线松动或者没插天线现场环境问题,信号穿透衰减终端接入远端AP终端个体问题 排查步骤: 1、AP的发射功率低 查看AP的射频功率,判…...
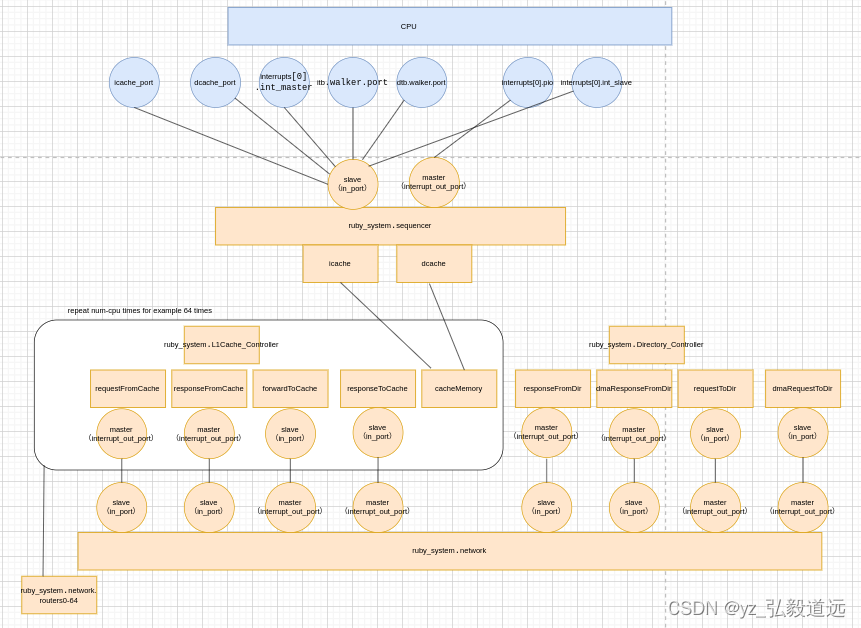
gem5 RubyPort: mem_request_port作用与连接 simple-MI_example.py
简介 回答这个问题:RubyPort的口下,一共定义了六个口,分别是mem_request_port,mem_response_port,pio_request_port,pio_response_port,in_ports, interrupt_out_ports,他们分别有什…...

无人机支持的空中无蜂窝大规模MIMO系统中上行链路分布式检测
无人机支持的空中无蜂窝大规模MIMO系统中上行链路分布式检测 无人机支持的空中无蜂窝大规模MIMO系统中上行链路分布式检测介绍题目一. 背景(解决的问题)二. 系统模型信道模型信道系数进行标准化 信道估计 和 数据传输信道估计上行数据传输 三. 具体的流程…...
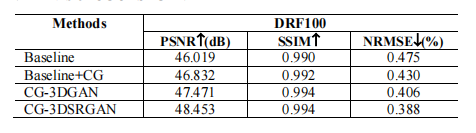
文献速递:生成对抗网络医学影像中的应用—— CG-3DSRGAN:用于从低剂量PET图像恢复图像质量的分类指导的3D生成对抗网络
文献速递:生成对抗网络医学影像中的应用—— CG-3DSRGAN:用于从低剂量PET图像恢复图像质量的分类指导的3D生成对抗网络 本周给大家分享文献的主题是生成对抗网络(Generative adversarial networks, GANs)在医学影像中的应用。文献…...

前端验收测试驱动开发
我们听说过很多关于测试驱动开发(TDD)的内容。那么什么是ATDD? ATDD代表验收测试驱动开发,这是一种定义验收标准并创建自动化测试来验证是否满足这些标准的软件开发方法。ATDD是一种协作方法,涉及客户、开发人员和测试…...
图像卷积操作
目录 一、互相关运算 二、卷积层 三、图像中目标的边缘检测 四、学习卷积核 五、特征映射和感受野 一、互相关运算 严格来说,卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation),而不是…...
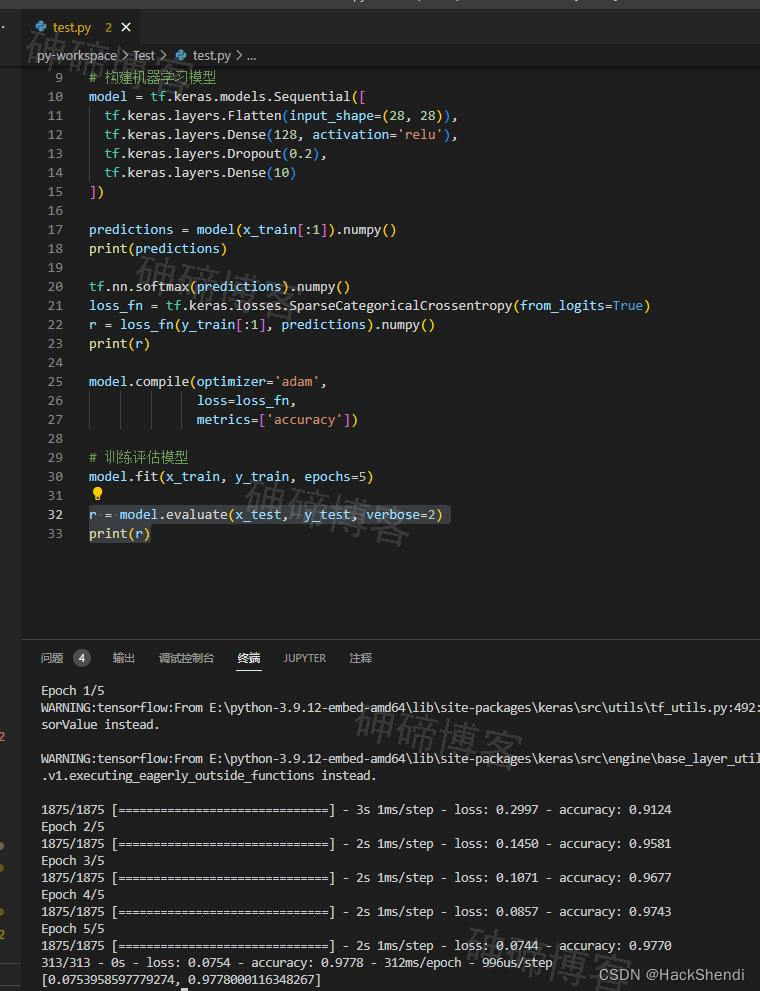
目标检测入门体验,技术选型,加载数据集、构建机器学习模型、训练并评估
Hi, I’m Shendi 1、目标检测入门体验,技术选型,加载数据集、构建机器学习模型、训练并评估 在最近有了个物体识别的需求,于是开始学习 在一番比较与询问后,最终选择 TensorFlow。 对于编程语言,我比较偏向Java或nod…...

【UE5插件推荐】运行时,通过HTTP / HTTPS下载文件(Runtime Files Downloader)
UE5 github Home gtreshchev/RuntimeFilesDownloader Wiki (github.com)...
信息论安全与概率论
目录 一. Markov不等式 二. 选择引理 三. Chebyshev不等式 四. Chernov上限 4.1 变量大于 4.2 变量小于 信息论安全中会用到很多概率论相关的上界,本文章将梳理几个论文中常用的定理,重点关注如何理解这些定理以及怎么用。 一. Markov不等式 假定…...
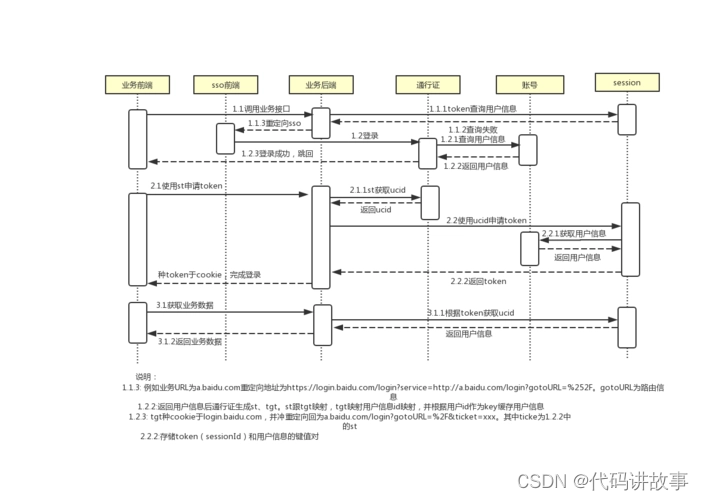
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统
各种不同语言分别整理的拿来开箱即用的8个开源免费单点登录(SSO)系统。 单点登录(SSO)是一个登录服务层,通过一次登录访问多个应用。使用SSO服务可以提高多系统使用的用户体验和安全性,用户不必记忆多个密…...

Netty Review - 优化Netty通信:如何应对粘包和拆包挑战
文章目录 概述Pre概述场景复现解决办法概览方式一: 特殊分隔符分包 (演示Netty提供的众多方案中的一种)流程分析 方式二: 发送长度(推荐) DelimiterBasedFrameDecoder 源码分析 概述 Pre Netty Review - 借助SimpleTalkRoom初体验…...

vue介绍以及基本指令
目录 一、vue是什么 二、使用vue的准备工作 三、创建vue项目 四、vue插值表达式 五、vue基本指令 六、key的作用 七、v-model 九、指令修饰符 一、vue是什么 Vue是一种用于构建用户界面的JavaScript框架。它可以帮助开发人员构建单页应用程序和复杂的前端应用程序。Vue…...

重塑数字生产力体系,生成式AI将开启云计算未来新十年?
科技云报道原创。 今天我们正身处一个历史的洪流,一个巨变的十字路口。生成式AI让人工智能技术完全破圈,带来了机器学习被大规模采用的历史转折点。 它掀起的新一轮科技革命,远超出我们今天的想象,这意味着一个巨大的历史机遇正…...

JFreeChart 生成图表,并为图表标注特殊点、添加文本标识框
一、项目场景: Java使用JFreeChart库生成图片,主要场景为将具体的数据 可视化 生成曲线图等的图表。 本篇文章主要针对为数据集生成的图表添加特殊点及其标识框。具体包括两种场景:x轴为 时间戳 类型和普通 数值 类型。(y轴都为…...

vue整合axios 未完
一、简介 1、介绍 axios前端异步请求库类似jouery ajax技术,axios用来在前端页面发起一个异步请求,请求之后页面不动,响应回来刷新页面局部;Axios 是一个基于 promise 的 HTTP 库,可以用在浏览器和 node.js 中 2、特…...

java代码编写twitter授权登录
在上一篇内容已经介绍了怎么申请twitter开放的API接口。 下面介绍怎么通过twitter提供的API,进行授权登录功能。 开发者页面设置 首先在开发者页面开启“用户认证设置”,点击edit进行信息编辑。 我的授权登录是个网页,并且只需要进行简单的…...
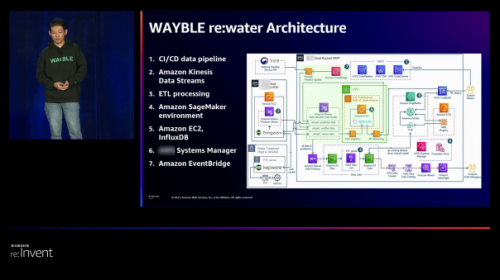
SK Ecoplant借助亚马逊云科技,海外服务器为环保事业注入新活力
在当今全球面临着资源紧缺和环境挑战的大背景下,数字技术所依赖的海外服务器正成为加速循环经济转型的关键利器。然而,很多企业在整合数字技术到运营中仍然面临着一系列挑战,依然存在低效流程导致的不必要浪费。针对这一问题,SK E…...
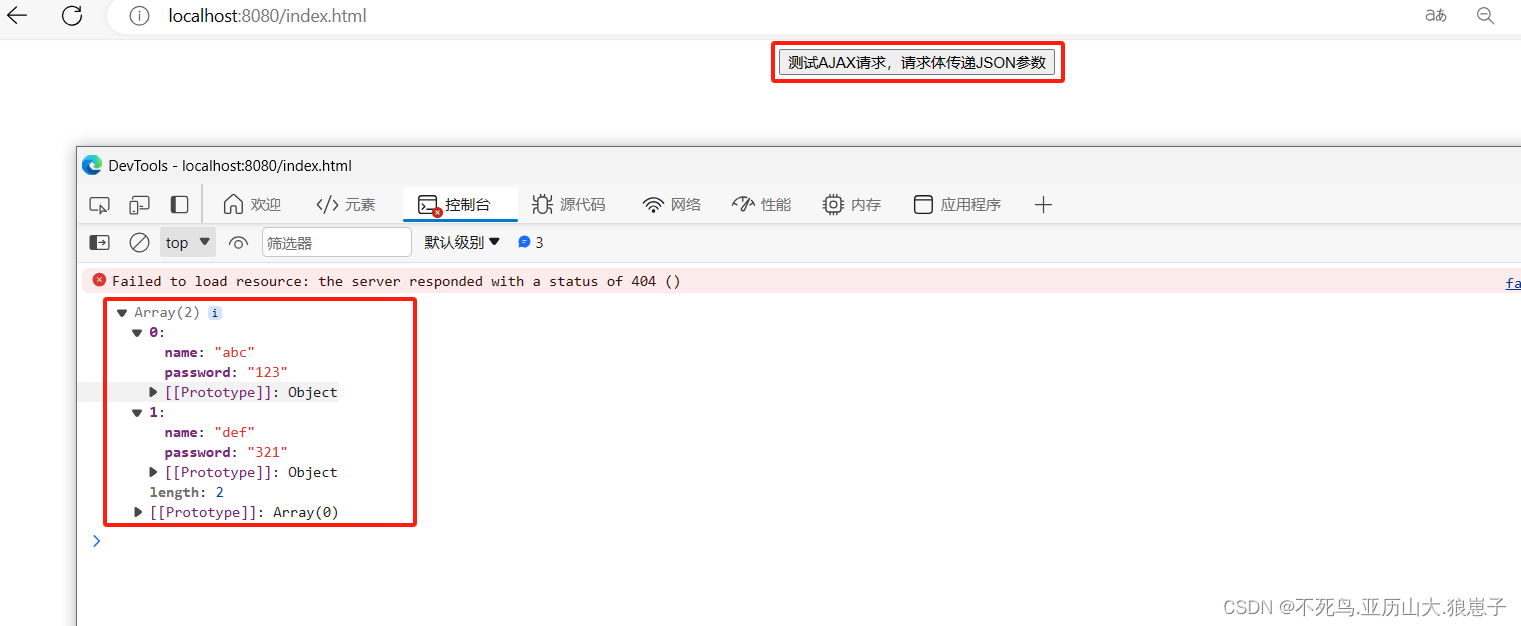
RPC(5):AJAX跨域请求处理
接上一篇RPC(4):HttpClient实现RPC之POST请求进行修改。 1 修改客户端项目 1.1 修改maven文件 修改后配置文件如下: <dependencyManagement><dependencies><dependency><groupId>org.springframework.b…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...
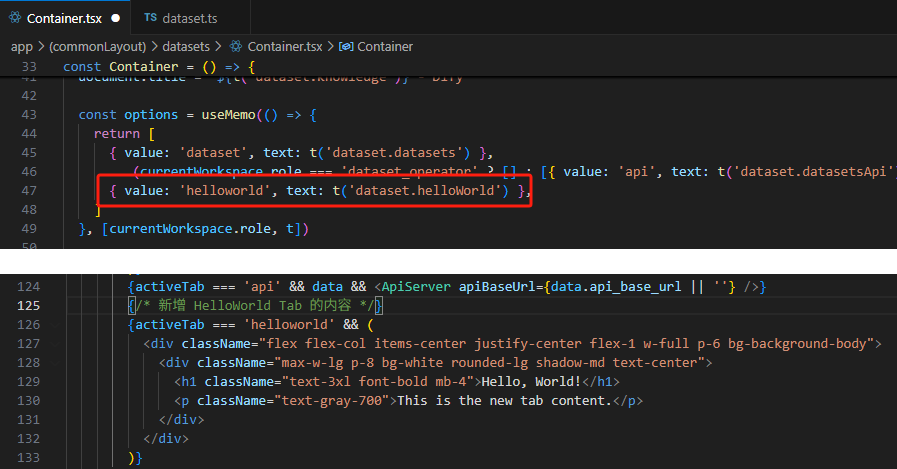
【技巧】dify前端源代码修改第一弹-增加tab页
回到目录 【技巧】dify前端源代码修改第一弹-增加tab页 尝试修改dify的前端源代码,在知识库增加一个tab页"HELLO WORLD",完成后的效果如下 [gif01] 1. 前端代码进入调试模式 参考 【部署】win10的wsl环境下启动dify的web前端服务 启动调试…...

VASP软件在第一性原理计算中的应用-测试GO
VASP软件在第一性原理计算中的应用 VASP是由维也纳大学Hafner小组开发的一款功能强大的第一性原理计算软件,广泛应用于材料科学、凝聚态物理、化学和纳米技术等领域。 VASP的核心功能与应用 1. 电子结构计算 VASP最突出的功能是进行高精度的电子结构计算ÿ…...

Spring AI中使用ChatMemory实现会话记忆功能
文章目录 1、需求2、ChatMemory中消息的存储位置3、实现步骤1、引入依赖2、配置Spring AI3、配置chatmemory4、java层传递conversaionId 4、验证5、完整代码6、参考文档 1、需求 我们知道大型语言模型 (LLM) 是无状态的,这就意味着他们不会保…...

电脑定时关机工具推荐
软件介绍 本文介绍一款轻量级的电脑自动关机工具,无需安装,使用简单,可满足定时关机需求。 工具简介 这款关机助手是一款无需安装的小型软件,文件体积仅60KB,下载后可直接运行,无需复杂配置。 使用…...

前端异步编程全场景解读
前端异步编程是现代Web开发的核心,它解决了浏览器单线程执行带来的UI阻塞问题。以下从多个维度进行深度解析: 一、异步编程的核心概念 JavaScript的执行环境是单线程的,这意味着在同一时间只能执行一个任务。为了不阻塞主线程,J…...
