管理类联考——数学——真题篇——按知识分类——代数——数列
【等差数列
⟹ \Longrightarrow ⟹ 通项公式: a n = a 1 + ( n − 1 ) d = a m + ( n − m ) d = n d + a 1 − d = A n + B a_n= a_1+(n-1)d =a_m+(n-m)d=nd+a_1-d=An+B an=a1+(n−1)d=am+(n−m)d=nd+a1−d=An+B ⟹ \Longrightarrow ⟹ A = d , B = a 1 − d A=d,B=a_1-d A=d,B=a1−d
⟹ \Longrightarrow ⟹ 求和公式: S n = n ( a 1 + a n ) 2 = n a n + 1 2 ( n 为偶数时,可虚拟小数) = n a 1 + n ( n − 1 ) 2 d = d 2 n 2 + ( a 1 − d 2 ) n = C n 2 + D n S_n=\frac{n(a_1+a_n)}{2}=na_{\frac{n+1}{2}}(n为偶数时,可虚拟小数)=na_1+\frac{n(n-1)}{2}d=\frac{d}{2}n^2+(a_1-\frac{d}{2})n=Cn^2+Dn Sn=2n(a1+an)=na2n+1(n为偶数时,可虚拟小数)=na1+2n(n−1)d=2dn2+(a1−2d)n=Cn2+Dn ⟹ \Longrightarrow ⟹ C = d 2 , D = a 1 − d 2 C=\frac{d}{2},D=a_1-\frac{d}{2} C=2d,D=a1−2d
其中,
S n = n a n + 1 2 S_n=na_{\frac{n+1}{2}} Sn=na2n+1 ⟹ \Longrightarrow ⟹ 相同的奇数项和之比 a k b k \frac{a_k}{b_k} bkak= S 2 k − 1 T 2 k − 1 \frac{S_{2k-1}}{T_{2k-1}} T2k−1S2k−1
S n = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2dn2+(a1−2d)n ⟹ \Longrightarrow ⟹ 对称轴为 n = − a 1 − d 2 2 × d 2 = 1 2 − a 1 d n=-\frac{a_1-\frac{d}{2}}{2×\frac{d}{2}}=\frac{1}{2}-\frac{a_1}{d} n=−2×2da1−2d=21−da1,最值取在最靠近对称轴的整数处
⟹ \Longrightarrow ⟹下标和:+
⟹ \Longrightarrow ⟹连续等长片段和/前n项和:新公差为 d n 2 dn^2 dn2
⟹ \Longrightarrow ⟹ 偶数项和与奇数项和之比:
若等差数列一共有 2 n 2n 2n项,则 S 偶 − S 奇 = n d , S 偶 S 奇 = a n + 1 a n S_偶-S_奇=nd,\frac{S_偶}{S_奇}=\frac{a_{n+1}}{a_n} S偶−S奇=nd,S奇S偶=anan+1。
若等差数列一共有 2 n — 1 2n—1 2n—1项,则 S 奇 − S 偶 = a n + 1 S_奇-S_偶=a_{n+1} S奇−S偶=an+1, S 奇 S 偶 = n n − 1 \frac{S_奇}{S_偶}=\frac{n}{n-1} S偶S奇=n−1n, S 2 n − 1 = S 奇 + S 偶 = ( 2 n − 1 ) a n S_{2n-1}=S_奇+S_偶=(2n-1)a_n S2n−1=S奇+S偶=(2n−1)an
⟹ \Longrightarrow ⟹ a n a_n an与 S n S_n Sn的快速转换: S n S_n Sn的二次项系数是 a n a_n an一次项系数的一半, a n a_n an的一次项系数是 S n S_n Sn二次项系数的二倍
⟹ \Longrightarrow ⟹ 轮换对称性
⟹ \Longrightarrow ⟹ 判定等差数列:①定义法: a n − a n − 1 = d a_n-a_{n-1}=d an−an−1=d;②通项形如 a n = A n + B a_n=An+B an=An+B;③前n项和形如 S n − C n 2 + D n S_n-Cn^2+Dn Sn−Cn2+Dn】
类比记忆法:牢记等差,引出等比
【等比数列
⟹ \Longrightarrow ⟹ 通项公式: a n = a 1 q n − 1 = a m q n − m = a k q n − k = a 1 q q n a_n=a_1q^{n-1}=a_mq^{n-m}=a_kq^{n-k}=\frac{a_1}{q}q^n an=a1qn−1=amqn−m=akqn−k=qa1qn
⟹ \Longrightarrow ⟹ 前n项和公式:当q=1时, S n = n a 1 ;当 q ≠ 1 时, S n = a 1 ( 1 − q n ) 1 − q = a 1 − a n q 1 − q = a 1 − a n + 1 1 − q S_n=na_1;当q≠1时,S_n=\frac{a_1(1-q^n)}{1-q}=\frac{a_1-a_nq}{1-q}=\frac{a_1-a_{n+1}}{1-q} Sn=na1;当q=1时,Sn=1−qa1(1−qn)=1−qa1−anq=1−qa1−an+1
⟹ \Longrightarrow ⟹下标和:×
⟹ \Longrightarrow ⟹ 连续等长片段和:新公比为 q n q^n qn
⟹ \Longrightarrow ⟹ 偶数项和与奇数项和之比:
若等比数列一共有 2 n 2n 2n项,则 S 偶 S 奇 = q \frac{S_偶}{S_奇}=q S奇S偶=q。
若等比数列一共有 2 n 一 1 2n一1 2n一1项,则 S 奇 S_奇 S奇与 S 偶 S_偶 S偶之间的关系无规律。】
【莫名巧合:等差数列
通项公式: a n = A n + B a_n=An+B an=An+B ⟹ \Longrightarrow ⟹ A = d , B = a 1 − d A=d,B=a_1-d A=d,B=a1−d
求和公式: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn ⟹ \Longrightarrow ⟹ C = d 2 , D = a 1 − d 2 C=\frac{d}{2},D=a_1-\frac{d}{2} C=2d,D=a1−2d
所以记住, A = d , B = a 1 − d , C = d 2 , D = a 1 − d 2 ,验证: A + B = C + D A=d,B=a_1-d,C=\frac{d}{2},D=a_1-\frac{d}{2},验证:A+B=C+D A=d,B=a1−d,C=2d,D=a1−2d,验证:A+B=C+D】
【递推数列
⟹ \Longrightarrow ⟹类等差数列 ⟹ \Longrightarrow ⟹累加法 ⟹ \Longrightarrow ⟹形如 a n + 1 = a n + f ( n ) 或 a n + 1 − a n = f ( n ) a_{n+1}=a_n+f(n)或a_{n+1}-a_n=f(n) an+1=an+f(n)或an+1−an=f(n) ⟹ \Longrightarrow ⟹写出若干项,再相加求解。
⟹ \Longrightarrow ⟹类等比数列 ⟹ \Longrightarrow ⟹累乘法 ⟹ \Longrightarrow ⟹ a n + 1 = a n ⋅ f ( n ) 或 a n + 1 a n = f ( n ) a_{n+1}=a_n·f(n)或\frac{a_{n+1}}{a_n}=f(n) an+1=an⋅f(n)或anan+1=f(n) ⟹ \Longrightarrow ⟹写出若干项,再相乘求解。
⟹ \Longrightarrow ⟹构造等差数列 ⟹ \Longrightarrow ⟹满足 b n + 1 − b n = 常数 b_{n+1}-b_n=常数 bn+1−bn=常数 ⟹ \Longrightarrow ⟹结论1:当看到 a n + 1 = a n c a n + 1 a_{n+1}=\frac{a_n}{ca_n+1} an+1=can+1an,那么{ 1 a n \frac{1}{a_n} an1}为等差数列;结论2:当看到 a n + 1 = q a n + q n a_{n+1}=qa_n+q^n an+1=qan+qn,两边同时除以 q n + 1 q^{n+1} qn+1来构造等差数列。
⟹ \Longrightarrow ⟹构造等比数列 ⟹ \Longrightarrow ⟹满足 b n + 1 b n = 常数 \frac{b_{n+1}}{b_n}=常数 bnbn+1=常数 ⟹ \Longrightarrow ⟹结论1:当看到 a n + 1 = q a n + c a_{n+1}= qa_n+c an+1=qan+c时,转化为 a n + 1 + k = q ( a n + k ) a_{n+1}+k=q(a_n+k) an+1+k=q(an+k),其中 k = c q − 1 k=\frac{c}{q-1} k=q−1c,构造等比数列即可。或者,类一次函数, a n + 1 = A ⋅ a n + B a_{n+1}=A·a_n+B an+1=A⋅an+B,构造等比数法, b n = a n + B A − 1 b_n=a_n+\frac{B}{A-1} bn=an+A−1B。结论2:当看到 a n + 1 = A a n + B n + C a_{n+1}=Aa_n+Bn+C an+1=Aan+Bn+C型,可化成 a n + 1 + p ( n + 1 ) + q = A ( a n + p n + q ) a_{n+1}+p(n+1)+q=A(a_n+pn+q) an+1+p(n+1)+q=A(an+pn+q)的形式来求通项。
⟹ \Longrightarrow ⟹没上述特点,列举前面若干项,寻找规律】
文章目录
- 数列
- 2023
- 2022
- 真题(2022-19)-代数-数列-等比数列-出现“三个数”-等比中项;-几何-平面几何
- 真题(2022-21)-代数-数列-等比数列-出现“三个数”,用等比中项- a c = b 2 ac=b^2 ac=b2;-代数-几何-平面几何-三角形-勾股定理
- 真题(2022-23)-代数-数列-等比数列-出现“三个数”,用等比中项;+代数-函数-一元二次函数
- 真题(2022-24)-代数-数列-等差数列-判定等差数列:①定义法: a n − a n − 1 = d a_n-a_{n-1}=d an−an−1=d;②通项形如 a n = A n + B a_n=An+B an=An+B;③前n项和形如 S n − C n 2 + D n S_n-Cn^2+Dn Sn−Cn2+Dn;-代数-数列-递推数列-形如 a n + 1 = a n + f ( n ) 或 a n + 1 − a n = f ( n ) a_{n+1}=a_n+f(n)或a_{n+1}-a_n=f(n) an+1=an+f(n)或an+1−an=f(n),称为类等差数列,可以写出若干项,再相加求解。=先写出若干项,再用累加法求解。
- 2021
- 真题(2021-02)-代数-数列-等差数列-出现“三”,用等差中项,2b=a+c;-前10题特值法、设未知数
- 真题(2021-24)-代数-数列-等比数列-等比数列判定-特征判断法-
- 真题(2021-25)-代数-数列-等差数列和等比数列;-几何-平面几何-三角形-相似;这种纯文字题,需要设未知数,但是很麻烦
- 2020
- 2019
- 真题(2019-15)-代数-数列-递推公式-构造等比数列-结论1:当看到 a n + 1 = q a n + c a_{n+1}= qa_n+c an+1=qan+c时,转化为 a n + 1 + k = q ( a n + k ) a_{n+1}+k=q(a_n+k) an+1+k=q(an+k),其中 k = c q − 1 k=\frac{c}{q-1} k=q−1c,构造等比数列即可。
- 真题(2019-16)-代数-数列-等比数列-数列的判定-
- 真题(2019-25)-代数-数列-等差数列-数列判定-特征判断法- S n S_n Sn的特征:形如一个没有常数项的一元二次函数: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn(C,D为常数)
- 2018
- 2017
- 真题(2017-03)-代数-数列-等差数列-出现“三”-等差中项-数列应用题
- 2016
- 真题(2016-24)-代数-数列-递推公式-直接计算法-举反例
- 2015
- 真题(2015-20)-E-代数-数列-等差数列
- 真题(2015-23)-代数-数列-等差数列-前n项和的最值-若 a 1 < 0 , d > 0 a_1<0,d>0 a1<0,d>0时, S n S_n Sn有最小值。
- 2014
- 真题(2014-07)-代数-数列-等差数列-出现“三”,用等差中项-
- 真题(2014-18)-代数-数列-等差数列&等比数列-既是等差数列又是等比数列的数列是非零的常数列
- 真题(2014-21)-A-代数-数列-等差数列;-方程-一元二次方程-判别式- △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
- 2013
- 真题(2013-13)-代数-数列-等差数列-下标和公式;-代数-方程-一元二次方程-韦达定理- x 1 + x 2 = − b / a x_1+x_2=-b/a x1+x2=−b/a
- 真题(2013-25)-代数-数列-递推公式-难度升级-中间段才出现周期
数列
2023
真题(2023-18)-代数-数列-等比数列-性质-递增需要 a 1 > 1 , q > 1 a_1>1,q>1 a1>1,q>1;-代数-方程-一元二次方程-根-因式分解


真题(2023-24)-代数-数列-等比数列- a n a_n an与 S n S_n Sn的关系(重要)


2022
有趣,2022年跟等比中项杠上了
真题(2022-19)-代数-数列-等比数列-出现“三个数”-等比中项;-几何-平面几何
19.在△ 𝐴𝐵𝐶 中,𝐷 为 𝐵𝐶 边上的点, 𝐵𝐷 、 𝐴𝐵 、𝐵𝐶成等比数列,则 ∠𝐵𝐴𝐶 = 90°。
(1)𝐵𝐷 = 𝐷𝐶。
(2) 𝐴𝐷 ⊥ 𝐵𝐶。

真题(2022-21)-代数-数列-等比数列-出现“三个数”,用等比中项- a c = b 2 ac=b^2 ac=b2;-代数-几何-平面几何-三角形-勾股定理
21.某直角三角形的三边长 𝑎 , 𝑏 , 𝑐 成等比数列,则能确定公比的值。
(1)𝑎 是直角边长。
(2)𝑐 是斜边长。

真题(2022-23)-代数-数列-等比数列-出现“三个数”,用等比中项;+代数-函数-一元二次函数
23.已知𝑎,𝑏为实数,则能确定𝑎的值。
(1)𝑎,𝑏,𝑎 + 𝑏成等比数列。
(2)𝑎(𝑎 + 𝑏) > 0。

真题(2022-24)-代数-数列-等差数列-判定等差数列:①定义法: a n − a n − 1 = d a_n-a_{n-1}=d an−an−1=d;②通项形如 a n = A n + B a_n=An+B an=An+B;③前n项和形如 S n − C n 2 + D n S_n-Cn^2+Dn Sn−Cn2+Dn;-代数-数列-递推数列-形如 a n + 1 = a n + f ( n ) 或 a n + 1 − a n = f ( n ) a_{n+1}=a_n+f(n)或a_{n+1}-a_n=f(n) an+1=an+f(n)或an+1−an=f(n),称为类等差数列,可以写出若干项,再相加求解。=先写出若干项,再用累加法求解。
24.已知正数列{ a n a_n an},则{ a n a_n an}是等差数列。
(1) a n + 1 2 − a n 2 = 2 n , n = 1 , 2 , . . . a_{n+1}^2-a_n^2=2n,n=1,2,... an+12−an2=2n,n=1,2,...。
(2) a 1 + a 3 = 2 a 2 a_1+a_3=2a_2 a1+a3=2a2。


2021
真题(2021-02)-代数-数列-等差数列-出现“三”,用等差中项,2b=a+c;-前10题特值法、设未知数
2.三位年轻人的年龄成等差数列,且最大与最小的两人年龄差的10倍是另一人的年龄,则三人中年龄最大的是( )。
A.19
B.20
C.21
D.22
E.23

真题(2021-24)-代数-数列-等比数列-等比数列判定-特征判断法-
24.已知数列{ a n a_n an},则数列{ a n a_n an}为等比数列。
(1) a n a n + 1 > 0 a_na_{n+1}>0 anan+1>0。
(2) a n + 1 2 − 2 a n 2 − a n a n + 1 = 0 a^2_{n+1}-2a^2_n-a_na_{n+1}=0 an+12−2an2−anan+1=0。

真题(2021-25)-代数-数列-等差数列和等比数列;-几何-平面几何-三角形-相似;这种纯文字题,需要设未知数,但是很麻烦
25.给定两个直角三角形,则这两个直角三角形相似。
(1)每个直角三角形边长成等比数列。
(2)每个直角三角形边长成等差数列。


2020
真题(2020-05)-代数-数列-等差数列-最值-等差数列的前n项和可以整理成一元二次函数的形式: S n = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2dn2+(a1−2d)n,对称轴为 n = − a 1 − d 2 2 × d 2 = 1 2 − a 1 d n=-\frac{a_1-\frac{d}{2}}{2×\frac{d}{2}}=\frac{1}{2}-\frac{a_1}{d} n=−2×2da1−2d=21−da1,最值取在最靠近对称轴的整数处。or-莫名巧合:等差数列-通项公式: a n = A n + B a_n=An+B an=An+B ⟹ \Longrightarrow ⟹ A = d , B = a 1 − d A=d,B=a_1-d A=d,B=a1−d;求和公式: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn ⟹ \Longrightarrow ⟹ C = d 2 , D = a 1 − d 2 C=\frac{d}{2},D=a_1-\frac{d}{2} C=2d,D=a1−2d,所以记住, A = d , B = a 1 − d , C = d 2 , D = a 1 − d 2 ,验证: A + B = C + D A=d,B=a_1-d,C=\frac{d}{2},D=a_1-\frac{d}{2},验证:A+B=C+D A=d,B=a1−d,C=2d,D=a1−2d,验证:A+B=C+D
5、若等差数列{ a n a_n an} 满足 a 1 = 8 a_1=8 a1=8,且 a 2 + a 4 = a 1 a_2+a_4=a_1 a2+a4=a1,则{ a n a_n an} 的前n 项和的最大值为( )
A.16
B.17
C.18
D.19
E.20


最值:
1.等差数列前n项和 S n S_n Sn有最值的条件
(1)若 a 1 < 0 , d > 0 a_1<0,d>0 a1<0,d>0时, S n S_n Sn有最小值。
(2)若 a 1 > 0 , d < 0 a_1>0,d<0 a1>0,d<0时, S n S_n Sn有最大值。
2.求解等差数列 S n S_n Sn最值的方法
(1)一元二次函数法
等差数列的前n项和可以整理成一元二次函数的形式: S n = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2dn2+(a1−2d)n,对称轴为 n = − a 1 − d 2 2 × d 2 = 1 2 − a 1 d n=-\frac{a_1-\frac{d}{2}}{2×\frac{d}{2}}=\frac{1}{2}-\frac{a_1}{d} n=−2×2da1−2d=21−da1,最值取在最靠近对称轴的整数处。
特别地,若 S m = S n S_m=S_n Sm=Sn,即 S m + n = 0 S_{m+n}=0 Sm+n=0时,对称轴为 m + n 2 \frac{m+n}{2} 2m+n。
(2) a n = 0 a_n=0 an=0法
最值一定在“变号”时取得,可令a=0,则有
① 若解得n为整数,则 S n = S n − 1 S_n=S_{n-1} Sn=Sn−1均为最值。例如,若解得n=6,则 S 6 = S 5 S_6=S_5 S6=S5为其最值。
② 若解得n为非整数,则当n取其整数部分m(m=[n])时, S m S_m Sm取到最值。例如,若解得n=6.9,则 S 6 S_6 S6为其最值。
真题(2020-11)-代数-数列-递推数列-没特点,列举若干项,找周期;类等差数列,累加法;类等比数列,累乘法。
11、已知数列{ a n a_n an}满足 a 1 = 1 a_1=1 a1=1, a 2 = 2 a_2=2 a2=2,且 a n + 2 = a n + 1 − a n ( n = 1 , 2 , 3 , . . . ) a_{n+2}=a_{n+1}-a_n(n=1,2,3,...) an+2=an+1−an(n=1,2,3,...),则 a 100 a_{100} a100=( )
A.1
B.-1
C.2
D.-2
E.0


2019
真题(2019-15)-代数-数列-递推公式-构造等比数列-结论1:当看到 a n + 1 = q a n + c a_{n+1}= qa_n+c an+1=qan+c时,转化为 a n + 1 + k = q ( a n + k ) a_{n+1}+k=q(a_n+k) an+1+k=q(an+k),其中 k = c q − 1 k=\frac{c}{q-1} k=q−1c,构造等比数列即可。
-秒杀:复杂选项(选多法):复杂选项可秒杀,按多的选(选多法),选项哪些因素出现多,就选哪些(90%准确率)1、99多,排除选项DE;2、-1,+1多,排除选项B。结果只能是A,C。看题干a1=0,C任何情况的不为0,所以选A。
15、设数列{ a n {a_n} an}满足 a 1 = 0 , a n + 1 − 2 a n = 1 a_1=0,a_{n+1}-2a_n=1 a1=0,an+1−2an=1,则 a 100 = a_{100}= a100=()
A. 2 99 − 1 2^{99}-1 299−1
B. 2 99 2^{99} 299
C. 2 99 + 1 2^{99}+1 299+1
D. 2 100 − 1 2^{100}-1 2100−1
E. 2 100 + 1 2^{100}+1 2100+1


秒杀:复杂选项(选多法):复杂选项可秒杀,按多的选(选多法),选项哪些因素出现多,就选哪些(90%准确率)1、99多,排除选项DE;2、-1,+1多,排除选项B。结果只能是A,C。看题干a1=0,C任何情况的不为0,所以选A。
真题(2019-16)-代数-数列-等比数列-数列的判定-
16、甲、乙、丙三人各自拥有不超过10本图书,甲再购入2本图书后,他们拥有的图书量构成等比数列,则能确定甲拥有图书的数量。
(1) 已知乙拥有的图书数量。
(2) 已知丙拥有的图书数量。


真题(2019-25)-代数-数列-等差数列-数列判定-特征判断法- S n S_n Sn的特征:形如一个没有常数项的一元二次函数: S n = C n 2 + D n S_n=Cn^2+Dn Sn=Cn2+Dn(C,D为常数)
25、设数列{ a n a_n an}的前n项和为 S n S_n Sn,则{ a n a_n an}等差。
(1) S n = n 2 + 2 n , n = 1 , 2 , 3 S_n=n^2+2n,n=1,2,3 Sn=n2+2n,n=1,2,3。
(2) S n = n + 2 n + 1 , n = 1 , 2 , 3 S_n=n^+2n+1,n=1,2,3 Sn=n+2n+1,n=1,2,3。


2018
真题(2018-07)-代数-数列-等比数列-无穷等比数列
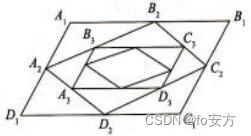
7.四边形 A 1 B 1 C 1 D 1 A_1B_1C_1D_1 A1B1C1D1是平行四边形, A 2 B 2 C 2 D 2 A_2B_2C_2D_2 A2B2C2D2是 A 1 B 1 C 1 D 1 A_1B_1C_1D_1 A1B1C1D1四边的中点, A 3 B 3 C 3 D 3 A_3B_3C_3D_3 A3B3C3D3分别是 A 2 B 2 C 2 D 2 A_2B_2C_2D_2 A2B2C2D2四边中点,依次下去,得到四边形序列 A n B n C n D n A_nB_nC_nD_n AnBnCnDn(n = 1、2、3…) ,设 A n B n C n D n A_nB_nC_nD_n AnBnCnDn面积为 S n S_n Sn,且 S 1 = 12 S_1=12 S1=12,则 S 1 + S 2 + S 3 + . . . = () S_1+S_2+S_3+...=() S1+S2+S3+...=()
A. 16 16 16
B. 20 20 20
C. 24 24 24
D. 28 28 28
E. 30 30 30




真题(2018-17)-B-代数-数列-等差数列-求和公式: S n = n ( a 1 + a n ) 2 = n a n + 1 2 ( n 为偶数时,可虚拟小数) = n a 1 + n ( n − 1 ) 2 d = d 2 n 2 + ( a 1 − d 2 ) n S_n=\frac{n(a_1+a_n)}{2}=na_{\frac{n+1}{2}}(n为偶数时,可虚拟小数)=na_1+\frac{n(n-1)}{2}d=\frac{d}{2}n^2+(a_1-\frac{d}{2})n Sn=2n(a1+an)=na2n+1(n为偶数时,可虚拟小数)=na1+2n(n−1)d=2dn2+(a1−2d)n
17.{ a n a_n an}等差数列,则能确定 a 1 + a 2 + . . . + a 9 a_1+a_2+...+a_9 a1+a2+...+a9的值。
(1)已知 a 1 a_1 a1的值。
(2)已知 a 5 a_5 a5的值。



2017
真题(2017-03)-代数-数列-等差数列-出现“三”-等差中项-数列应用题
3.甲、乙、丙三种货车载重量成等差数列,2 辆甲种车和 1 辆乙种车的满载量为 95 吨,1辆甲种车和 3 辆丙种车载重量为 150 吨,则用甲、乙、丙各一辆车一次最多运送货物为( )吨。
A.125
B.120
C.115
D.110
E.105


2016
真题(2016-24)-代数-数列-递推公式-直接计算法-举反例
24.已知数列 a 1 , a 2 , a 3 , . . . , a 10 a_1,a_2,a_3,...,a_{10} a1,a2,a3,...,a10,则 a 1 − a 2 + a 3 − . . . + a 9 − a 10 ≥ 0 a_1-a_2+a_3-...+a_9-a_{10}≥0 a1−a2+a3−...+a9−a10≥0
(1) a n ≥ a n + 1 , n = 1 , 2 , . . . , 9 a_n≥a_{n+1},n=1,2,...,9 an≥an+1,n=1,2,...,9
(2) a n 2 ≥ a n + 1 2 , n = 1 , 2 , . . . , 9 a_n^2≥a_{n+1}^2,n=1,2,...,9 an2≥an+12,n=1,2,...,9

2015
真题(2015-20)-E-代数-数列-等差数列
20.设{ a n a_n an}是等差数列,则能确定数列{ a n a_n an}。
(1) a 1 + a 6 = 0 a_1+a_6=0 a1+a6=0
(2) a 1 a 6 = − 1 a_1a_6=-1 a1a6=−1

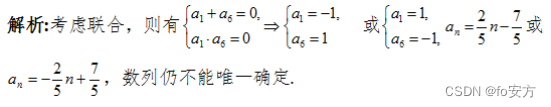
真题(2015-23)-代数-数列-等差数列-前n项和的最值-若 a 1 < 0 , d > 0 a_1<0,d>0 a1<0,d>0时, S n S_n Sn有最小值。
23.已知数列{ a n a_n an}是公差大于零的等差数列,{ S n S_n Sn}是{ a n a_n an}的前n 项和。则 S n ≥ S 10 , n = 1 , 2 , . . . S_n≥S_{10},n=1,2,... Sn≥S10,n=1,2,...
(1) a 10 = 0 a_{10}=0 a10=0
(2) a 11 a 10 < 0 a_{11}a_{10}<0 a11a10<0



2014
真题(2014-07)-代数-数列-等差数列-出现“三”,用等差中项-
7.已知{ a n a_n an}为等差数列,且 a 2 − a 5 + a 8 = 9 a_2-a_5+a_8=9 a2−a5+a8=9 ,则 a 1 + a 2 + . . . + a 9 = () a_1+a_2+...+a_9=( ) a1+a2+...+a9=()
A.27
B.45
C.54
D.81
E.182
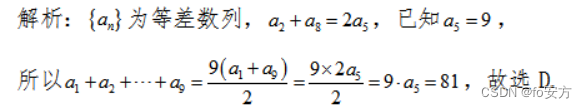

真题(2014-18)-代数-数列-等差数列&等比数列-既是等差数列又是等比数列的数列是非零的常数列
18.甲、乙、丙三人的年龄相同
(1)甲、乙、丙的年龄成等差数列
(2)甲、乙、丙的年龄成等比数列


真题(2014-21)-A-代数-数列-等差数列;-方程-一元二次方程-判别式- △ = b 2 − 4 a c △=b^2-4ac △=b2−4ac
21.方程 x 2 + 2 ( a + b ) x + c 2 = 0 x^2+2(a+b)x+c^2=0 x2+2(a+b)x+c2=0 有实根。
(1) a, b, c 是一个三角形的三边长。
(2)实数a, b, c 成等差数列。


2013
真题(2013-13)-代数-数列-等差数列-下标和公式;-代数-方程-一元二次方程-韦达定理- x 1 + x 2 = − b / a x_1+x_2=-b/a x1+x2=−b/a
13.已知{ a n a_n an}为等差数列,若 a 2 a_2 a2和 a 10 a_{10} a10是方程 x 2 − 10 x − 9 = 0 x^2-10x-9=0 x2−10x−9=0的两个根,则 a 5 + a 7 = a_5+a_7= a5+a7=( )。
A. − 10 -10 −10
B. − 9 -9 −9
C. 9 9 9
D. 10 10 10
E. 12 12 12

真题(2013-25)-代数-数列-递推公式-难度升级-中间段才出现周期
25.设 a 1 = 1 , a 2 = k , . . . , a n + 1 = ∣ a n − a n − 1 ∣ , ( n ≥ 2 ) a_1=1,a_2=k,...,a_{n+1}=|a_n-a_{n-1}|,(n≥2) a1=1,a2=k,...,an+1=∣an−an−1∣,(n≥2) ,则 a 100 + a 101 + a 102 = 2 a_{100}+a_{101}+a_{102}=2 a100+a101+a102=2
(1) k = 2 k = 2 k=2
(2)k 是小于 20 的正整数



相关文章:

管理类联考——数学——真题篇——按知识分类——代数——数列
【等差数列 ⟹ \Longrightarrow ⟹ 通项公式: a n a 1 ( n − 1 ) d a m ( n − m ) d n d a 1 − d A n B a_n a_1(n-1)d a_m(n-m)dnda_1-dAnB ana1(n−1)dam(n−m)dnda1−dAnB ⟹ \Longrightarrow ⟹ A d , B a 1 − d Ad&#x…...
.net core webapi 自定义异常过滤器
1.定义统一返回格式 namespace webapi;/// <summary> /// 统一数据响应格式 /// </summary> public class Results<T> {/// <summary>/// 自定义的响应码,可以和http响应码一致,也可以不一致/// </summary>public int Co…...
SuperMap iServer发布的ArcGIS REST 地图服务如何通过ArcGIS API加载
作者:yx 文章目录 一、发布服务二、代码加载三、结果展示 一、发布服务 SuperMap iServer支持将地图发布为ArcGIS REST地图服务,您可以在发布服务时直接勾选ArcGIS REST地图服务,如下图所示: 也可以在已发布的地图服务中&#x…...

python调用GPT API
每次让gpt给我生成一个调用api的程序时,他经常会调用以前的一些api的方法,导致我的程序运行错误,所以这期记录一下使用新的方法区调用api 参考网址 Migration Guide,这里简要地概括了一下新版本做了哪些更改 OpenAI Python API l…...
ModuleNotFoundError: No module named ‘tensorflow‘
直接运行pip install tensorflow安装成功之后,发现版本是tensorflow2.15.0 python的版本是3.9版本 导入包:import tensorflow 打包xxx.exe,调用之后提示错误 ModuleNotFoundError: No module named tensorflow 最后发现特定的python的版本对应特定的t…...

智能优化算法应用:基于鹰栖息算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于鹰栖息算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于鹰栖息算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.鹰栖息算法4.实验参数设定5.算法结果6.参考文…...
自定义Taro上传图片hooks(useUploadImg)
有两个方法需要提前引入 FileUtil(上传文件的方法)、to(对请求接口返回做了二次处理,数据和错误提示等) //FileUtil export namespace FileUtil {const env {timeout: 10000,uploadImageUrl: "阿里云的地址",};const genPolicy …...
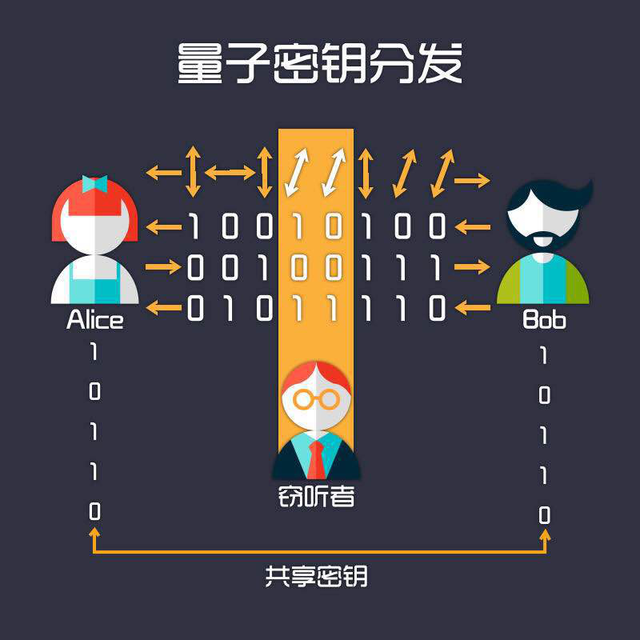
量子密码学简介
量子密码学(英语:Quantum cryptography)泛指利用量子力学的特性来加密的科学。量子密码学最著名的例子是量子密钥分发,而量子密钥分发提供了通信两方安全传递密钥的方法,且该方法的安全性可被信息论所证明。目前所使用…...
使用docker创建自己的Android编译容器
文章目录 背景步骤1.创建Dockerfile2.编写Dockerfile指令3.编译4.使用 背景 每次拿到新机器或者系统重装,最麻烦的就是各种环境配置,最近学习了一下docker的知识,用dockerfile创建一个Android编译容器,这样就不用每次都吭哧吭哧的…...

4-Docker命令之docker load
1.docker load介绍 docker load命令是用来将从tar归档文件载入镜像 docker load命令相对应的命令是docker save 2.docker load用法 docker load [参数] [root@centos79 ~]# docker load --helpUsage: docker load [OPTIONS]Load an image from a tar archive or STDINAli…...
微信小程序格创校园跑腿小程序源码v1.1.64+前端
简介: 版本号:1.1.64 – 多学校版本 本次更新内容: 订单问题修复 (无需上传小程序) 版本号:1.1.63 – 多学校版本 本次更新内容: 失物招领增加内容安全接口; 认证增加性别选…...

【单元测试】测还是不测,这是一个问题
这篇文章也可以在我的博客中查看 “册”那!! 相信大家从小就被千叮万嘱要做单元测试。然后秉承这一信念,成为了一个测试狂魔。凡有代码,测!覆盖!最终,一波操作猛如虎:467测试&…...
)
Global Mapper SDK 19 中文开发文档(八)
7.2.8 GM_DBUtil (1)声明 public static class GM_DBUtil (2)方法 方法描述DBGetTableList获取指定空间数据库中的表列表DBIsDatabaseFile指示输入文件是否为数据库(Esri地理数据库、Spatialite等)DBMa…...

es检索之复合检索
背景:向量检索是文本相似度检索,现在增加新的字段进行过滤,如果以filter方式进行过滤,那么最终结果不保证有topK个,甚至一个都没有,因为它是先进行topK个向量召回,再进行filter。 当然有人建议采用scriptScore方式进行检索,但此方式可能造成请求压力过大,内存消耗。 …...

09.list 容器
9、list 容器 功能: 将数据进行链式存储 链表(list)是一种物理存储单元上非连续的存储结构,数据元素的逻辑顺序是通过链表中的指针链接实现的 链表的组成: 链表由一系列结点组成 结点的组成: 一个是存…...

速盾网络:网站用速盾cdn的好处
随着互联网的快速发展,网站的速度和稳定性成为了用户访问体验的关键因素。为了提高网站的性能和可用性,许多网站开始使用CDN(Content Delivery Network)服务。本文将介绍CDN的基本概念、工作原理以及使用CDN的好处。一、CDN的基本…...

Centos7在安装Graylog时新安装MongoDB报错端口不监听服务不启动无法运行启动失败
由于虚拟机服务器上需要安装Graylog需要安装MongoDB,尝试官网下载安装包,和yum安装均无法正常启动,折腾了好几天,重装了十几次,网上搜索了很多很多资料,均无法正常运行,百度上搜索各种文档&…...
)
Spark Machine Learning进行数据挖掘的简单应用(兴趣预测问题)
数据挖掘的过程 数据挖掘任务主要分为以下六个步骤: 1.数据预处理2.特征转换3.特征选择4.训练模型5.模型预测6.评估预测结果 数据准备 这里准备了20条关于不同地区、不同性别、不同身高、体重…的人的兴趣数据集(命名为hobby.csv): id,h…...

DRF从入门到精通二(Request源码分析、DRF之序列化、反序列化、反序列化校验、序列化器常用字段及参数、source、定制字段、保存数据)
文章目录 一、Request对象源码分析区分原生request和新生request新的request还能像原来的reqeust一样使用吗源码片段分析总结: 二、DRF之序列化组件序列化介绍序列化步骤序列化组件的基本使用反序列化基本使用反序列化的新增反序列化的新增删除单条 反序列化的校验序…...

Flink系列之:Upsert Kafka SQL 连接器
Flink系列之:Upsert Kafka SQL 连接器 一、Upsert Kafka SQL 连接器二、依赖三、完整示例四、可用元数据五、键和值格式六、主键约束七、一致性保证八、为每个分区生成相应的watermark九、数据类型映射 一、Upsert Kafka SQL 连接器 Scan Source: Unbounded 、Sink…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...
