基于矩阵乘的CUDA编程优化过程
背景:网上很多关于矩阵乘的编程优化思路,本着看理论分析万遍,不如实际代码写一遍的想法,大概过一下优化思路。
矩阵乘的定义如下,约定矩阵的形状及存储方式为: A[M, K], B[K, N], C[M, N]。
CPU篇
朴素实现方法
按照常规的思路,实现矩阵乘时如下的3层for循环。
#define OFFSET(row, col, ld) ((row) * (ld) + (col))
void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K)
{for (int m = 0; m < M; m++) {for (int n = 0; n < N; n++) {float psum = 0.0;for (int k = 0; k < K; k++) {psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];}c[OFFSET(m, n, N)] = psum;}}
}数据访存连续的优化
矩阵B的存储默认为N方向连续,所以可以将上面的第2,3层循环互换顺序,这样B的取数就不会跨行了,而是连续取数,达到访问连续的效果。
void cpuSgemm_1(float *a, float *b, float *c, const int M, const int N, const int K)
{for (int m = 0; m < M; m++) {for (int k = 0; k < K; k++) {for (int n = 0; n < N; n++){c[OFFSET(m, n, N)] += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];} }}
}数据重排/数据复用的优化
上面将M,N,K的for循环调整为M,K,N的循环顺序,导致我们K方向累加不能缓存了,增加了多次访问C矩阵的开销,所以我们不放先直接将B矩阵转置处理,然后再按照原始的M,N,K的for循环来处理。
void cpuSgemm_2(float *a, float *b, float *c, const int M, const int N, const int K)
{float* b1=(float*) malloc(sizeof(float)*K*N);for(int i=0; i<K; i++){for (int j=0; j<N; j++){b1[OFFSET(j,i,K)]= b[OFFSET(i,j,N)];}}for (int m = 0; m < M; m++) {for (int n = 0; n < N; n++) {float psum = 0.0;for (int k = 0; k < K; k++) {psum += a[OFFSET(m, k, K)] * b1[OFFSET(n, k, K)];}c[OFFSET(m, n, N)] = psum;}}
}性能表现
如下是测试CPU环境下这几种方法的时间情况,其中M=N=512, K =256。可以发现经过优化后的代码在时间上是逐步减少的。
CPU的优化思路还有其他的,比如循环展开,intrinsic函数,基于cache的矩阵切分等,注意本文并没有都实现出来。
cpuSgemm, Time measured: 416889 microseconds.
cpuSgemm_1, Time measured: 405259 microseconds.
cpuSgemm_2, Time measured: 238786 microseconds.GPU篇
grid线程循环矩阵乘法
输出矩阵C有M*N个点,每个点是K个数的乘积和,所以可以定义每个线程计算K个点的乘积和,即grid线程循环矩阵乘法。
__global__ void matrix_multiply_gpu_0(float*a, float*b, float*c, int M, int N, int K)
{int tidx =threadIdx.x;int bidx = blockIdx.x;int idx = bidx * blockDim.x +tidx;int row = idx/N;int col = idx%N;if(row<M && col < N){float tmp =0.0;for(int k=0; k<K; k++){tmp+=a[row*K+k] * b[k*N+col];}c[row*N+col] = tmp;}
}block线程循环矩阵乘法
grid内线程循环的矩阵乘法有如下缺憾:一个block内线程可能需要计算C矩阵不同行的矩阵元素,block内thread对相应的A矩阵访存不一致,导致无法广播和额外的访存开销,导致执行时间增加。
针对这个问题,可以做如下改进:每个block计算C矩阵的一行,block内的thread以固定跳步步长blockDim.x的方法循环计算C矩阵的一行,每一行启动一个block,共计M个block。
__global__ void matrix_multiply_gpu_1(float*a, float*b, float*c, int M, int N, int K)
{int tidx =threadIdx.x;int bidx = blockIdx.x;float tmp;for(;bidx<M; bidx += gridDim.x){for(;tidx<N; tidx+=blockDim.x ){tmp=0.0;for(int k=0; k<K; k++){tmp+=a[bidx*K +k] * b[k*N+tidx];}c[bidx*N+tidx] = tmp;} }
}
行共享存储矩阵乘法
共享存储与L1 Cache同级,其访存延迟较全局存储小一个量级。用共享存储代替全局存储是GPU最重要的优化手段之一。采用共享存储优化的关键是数据复用,数据复用次数越多,共享存储优化可获得的收益也越高。
在block循环乘法中,1个block内所有thread都会用到A矩阵的一行,此时与B矩阵每一列相乘,A矩阵中该行复用了N次。故可以考虑将A矩阵的一行读入shared memory,运算时候从shared memory读取相应的数据。
注意代码中TILE_WIDTH>=K。
#define TILE_WIDTH 256
__global__ void matrix_multiply_gpu_2(float*a, float*b, float*c, int M, int N, const int K)
{__shared__ float data[TILE_WIDTH];int tid = threadIdx.x;int row = blockIdx.x;int i,j;for(i=tid; i<K; i+=blockDim.x){data[i]=a[row*K +i];}__syncthreads();float tmp;for(j=tid; j<N; j+=blockDim.x){tmp=0.0;for(int k=0; k<K; k++){tmp += data[k]*b[k*N+j];}c[row*N+j] = tmp;}
}
分块共享存储矩阵乘法
根据上面共享存储的理解,我们很自然的想到把B矩阵也考虑数据复用,所以可以同时把A,B矩阵都分成棋盘似的小尺寸的数据块,从全局内存读取到共享内存,这样可以有效降低数据访问时间,充分复用矩阵乘的局部数据。
#define TILE_SIZE 32
__global__ void matrix_multiply_gpu_3(float*a, float*b, float*c, int M, int N, const int K)
{__shared__ float matA[TILE_SIZE][TILE_SIZE];__shared__ float matB[TILE_SIZE][TILE_SIZE];int bx = blockIdx.x;int by = blockIdx.y;int tx = threadIdx.x;int ty = threadIdx.y;int Col = bx * TILE_SIZE + tx;int Row = by * TILE_SIZE + ty;float Pervalue = 0.0;for(int i = 0;i < K / TILE_SIZE;i++) {matA[ty][tx] = a[Row * K + (i * TILE_SIZE + tx)];matB[ty][tx] = b[Col + (i * TILE_SIZE + ty) * N];__syncthreads();for(int k = 0;k < TILE_SIZE;k++) Pervalue += matA[ty][k] * matB[k][tx];__syncthreads();}c[Row * N + Col] = Pervalue;}性能表现
利用nvprof工具,统计各个核函数的执行时间如下,可以发现每一步优化思路都能直观的带来的性能提升。
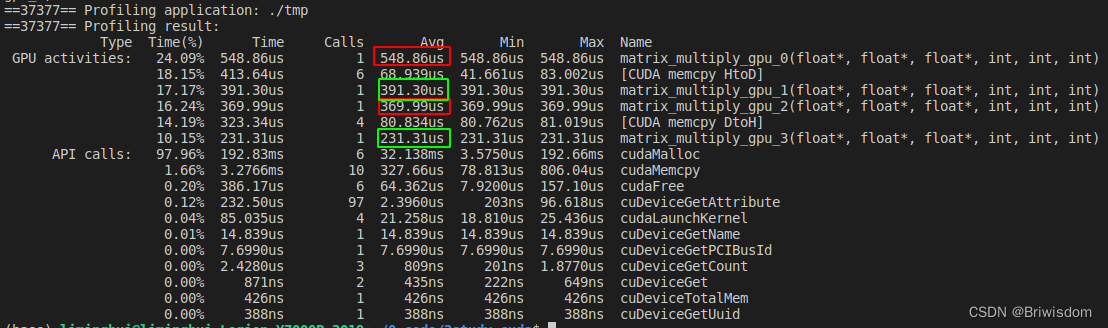
完整代码:
GitHub - Briwisdom/study_CUDA_examples: some demos for study CUDA program.
#include <iostream>
#include <chrono>using namespace std;#define OFFSET(row, col, ld) ((row) * (ld) + (col))void initDate(float *arr,int Len, bool randFlag=true)
{if (randFlag){for (int i = 0; i < Len; i++) {arr[i] = rand()/1000000;}}else{float value =0.0;for (int i = 0; i < Len; i++) {arr[i] = value;}}
}void compare_result(float *x, float *y, int n, char *name)
{int cnt=0;for (int i=0; i<n; i++){if (x[i]!=y[i]){cnt++;printf("x= %f, y= %f\n", x[i],y[i]);}}printf("%s, ", name);if(cnt ==0)printf("result matched.\n");elseprintf("something error! result not match number = %d int total number: %d .\n", cnt, n);}void cpuSgemm(float *a, float *b, float *c, const int M, const int N, const int K)
{for (int m = 0; m < M; m++) {for (int n = 0; n < N; n++) {float psum = 0.0;for (int k = 0; k < K; k++) {psum += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];}c[OFFSET(m, n, N)] = psum;}}
}void cpuSgemm_1(float *a, float *b, float *c, const int M, const int N, const int K)
{for (int m = 0; m < M; m++) {for (int k = 0; k < K; k++) {for (int n = 0; n < N; n++){c[OFFSET(m, n, N)] += a[OFFSET(m, k, K)] * b[OFFSET(k, n, N)];} }}
}void cpuSgemm_2(float *a, float *b, float *c, const int M, const int N, const int K)
{float* b1=(float*) malloc(sizeof(float)*K*N);for(int i=0; i<K; i++){for (int j=0; j<N; j++){b1[OFFSET(j,i,K)]= b[OFFSET(i,j,N)];}}for (int m = 0; m < M; m++) {for (int n = 0; n < N; n++) {float psum = 0.0;for (int k = 0; k < K; k++) {psum += a[OFFSET(m, k, K)] * b1[OFFSET(n, k, K)];}c[OFFSET(m, n, N)] = psum;}}
}void operation(void (*func)(float*,float*, float*, int, int, int), float *a, float *b, float *c, const int M, const int N, const int K, int repeat, char* name)
{auto begin0 = std::chrono::high_resolution_clock::now();for(int i=0; i<repeat; i++){(*func)(a,b,c, M, N, K);}auto end0 = std::chrono::high_resolution_clock::now();auto elapsed0 = std::chrono::duration_cast<std::chrono::microseconds>(end0 - begin0);printf("%s, Time measured: %d microseconds.\n", name, int(elapsed0.count()/repeat));
}__global__ void matrix_multiply_gpu_0(float*a, float*b, float*c, int M, int N, int K)
{int tidx =threadIdx.x;int bidx = blockIdx.x;int idx = bidx * blockDim.x +tidx;int row = idx/N;int col = idx%N;if(row<M && col < N){float tmp =0.0;for(int k=0; k<K; k++){tmp+=a[row*K+k] * b[k*N+col];}c[row*N+col] = tmp;}
}__global__ void matrix_multiply_gpu_1(float*a, float*b, float*c, int M, int N, int K)
{int tidx =threadIdx.x;int bidx = blockIdx.x;float tmp;for(;bidx<M; bidx += gridDim.x){for(;tidx<N; tidx+=blockDim.x ){tmp=0.0;for(int k=0; k<K; k++){tmp+=a[bidx*K +k] * b[k*N+tidx];}c[bidx*N+tidx] = tmp;} }
}#define TILE_WIDTH 256
__global__ void matrix_multiply_gpu_2(float*a, float*b, float*c, int M, int N, const int K)
{__shared__ float data[TILE_WIDTH];int tid = threadIdx.x;int row = blockIdx.x;int i,j;for(i=tid; i<K; i+=blockDim.x){data[i]=a[row*K +i];}__syncthreads();float tmp;for(j=tid; j<N; j+=blockDim.x){tmp=0.0;for(int k=0; k<K; k++){tmp += data[k]*b[k*N+j];}c[row*N+j] = tmp;}
}#define TILE_SIZE 32
__global__ void matrix_multiply_gpu_3(float*a, float*b, float*c, int M, int N, const int K)
{__shared__ float matA[TILE_SIZE][TILE_SIZE];__shared__ float matB[TILE_SIZE][TILE_SIZE];int bx = blockIdx.x;int by = blockIdx.y;int tx = threadIdx.x;int ty = threadIdx.y;int Col = bx * TILE_SIZE + tx;int Row = by * TILE_SIZE + ty;float Pervalue = 0.0;for(int i = 0;i < K / TILE_SIZE;i++) {matA[ty][tx] = a[Row * K + (i * TILE_SIZE + tx)];matB[ty][tx] = b[Col + (i * TILE_SIZE + ty) * N];__syncthreads();for(int k = 0;k < TILE_SIZE;k++) Pervalue += matA[ty][k] * matB[k][tx];__syncthreads();}c[Row * N + Col] = Pervalue;}int main()
{int M=512;int N=512;int K=256;float *a = (float*) malloc(M*K * sizeof(float));float *b = (float*) malloc(N*K * sizeof(float));float *c = (float*) malloc(M*N * sizeof(float));float *c1 = (float*) malloc(M*N * sizeof(float));float *c2 = (float*) malloc(M*N * sizeof(float));float *c_gpu_0 = (float*) malloc(M*N * sizeof(float));float *c_gpu_1 = (float*) malloc(M*N * sizeof(float));float *c_gpu_2 = (float*) malloc(M*N * sizeof(float));float *c_gpu_3 = (float*) malloc(M*N * sizeof(float));initDate(a,M*K);initDate(b,N*K);initDate(c, M*N, false);initDate(c1, M*N, false);initDate(c2, M*N, false);initDate(c_gpu_0, M*N, false);initDate(c_gpu_1, M*N, false);initDate(c_gpu_2, M*N, false);initDate(c_gpu_3, M*N, false);//ensure result is right.cpuSgemm(a,b,c,M,N,K);cpuSgemm_1(a,b,c1,M,N,K);cpuSgemm_2(a,b,c2,M,N,K); compare_result(c, c1, M*N,"sgemm1");compare_result(c, c2, M*N,"sgemm2");//test the prerformance.int repeat =10;operation(cpuSgemm,a,b,c,M,N,K,repeat,"cpuSgemm");operation(cpuSgemm_1,a,b,c1,M,N,K,repeat,"cpuSgemm_1");operation(cpuSgemm_2,a,b,c2,M,N,K,repeat,"cpuSgemm_2");float* d_a, *d_b, *d_c0, *d_c1, *d_c2, *d_c3;cudaMalloc((void**) &d_a, sizeof(float)*(M*K));cudaMalloc((void**) &d_b, sizeof(float)*(N*K));cudaMalloc((void**) &d_c0, sizeof(float)*(M*N));cudaMalloc((void**) &d_c1, sizeof(float)*(M*N));cudaMalloc((void**) &d_c2, sizeof(float)*(M*N));cudaMalloc((void**) &d_c3, sizeof(float)*(M*N));cudaMemcpy(d_a, a, sizeof(float)*M*K, cudaMemcpyHostToDevice);cudaMemcpy(d_b, b, sizeof(float)*N*K, cudaMemcpyHostToDevice);int threadnum=64;int blocks =(M*N+threadnum-1)/threadnum;cudaMemcpy(d_c0, c_gpu_0, sizeof(float)*M*N, cudaMemcpyHostToDevice);matrix_multiply_gpu_0<<<blocks, threadnum>>>(d_a, d_b, d_c0, M, N, K);cudaMemcpy(c_gpu_0, d_c0, sizeof(float)*M*N, cudaMemcpyDeviceToHost);compare_result(c, c_gpu_0, M*N,"gpu_0");cudaFree(d_c0);cudaMemcpy(d_c1, c_gpu_1, sizeof(float)*M*N, cudaMemcpyHostToDevice);matrix_multiply_gpu_1<<<M, threadnum>>>(d_a, d_b, d_c1, M, N, K);cudaMemcpy(c_gpu_1, d_c1, sizeof(float)*M*N, cudaMemcpyDeviceToHost);compare_result(c, c_gpu_1, M*N,"gpu_1");cudaFree(d_c1);cudaMemcpy(d_c2, c_gpu_2, sizeof(float)*M*N, cudaMemcpyHostToDevice);matrix_multiply_gpu_2<<<M, threadnum>>>(d_a, d_b, d_c2, M, N, K);cudaMemcpy(c_gpu_2, d_c2, sizeof(float)*M*N, cudaMemcpyDeviceToHost);compare_result(c, c_gpu_2, M*N,"gpu_2");cudaFree(d_c2);threadnum=32;dim3 gridSize(M / threadnum,N / threadnum);dim3 blockSize(threadnum,threadnum);cudaMemcpy(d_c3, c_gpu_3, sizeof(float)*M*N, cudaMemcpyHostToDevice);matrix_multiply_gpu_3<<<gridSize, blockSize>>>(d_a, d_b, d_c3, M, N, K);cudaMemcpy(c_gpu_3, d_c3, sizeof(float)*M*N, cudaMemcpyDeviceToHost);compare_result(c, c_gpu_3, M*N,"gpu_3");cudaFree(d_c3);free(a);free(b);free(c);free(c1);free(c2);free(c_gpu_0);free(c_gpu_1);free(c_gpu_2);free(c_gpu_3);cudaFree(d_a);cudaFree(d_b);}相关文章:

基于矩阵乘的CUDA编程优化过程
背景:网上很多关于矩阵乘的编程优化思路,本着看理论分析万遍,不如实际代码写一遍的想法,大概过一下优化思路。 矩阵乘的定义如下,约定矩阵的形状及存储方式为: A[M, K], B[K, N], C[M, N]。 CPU篇 朴素实现方法 按照…...
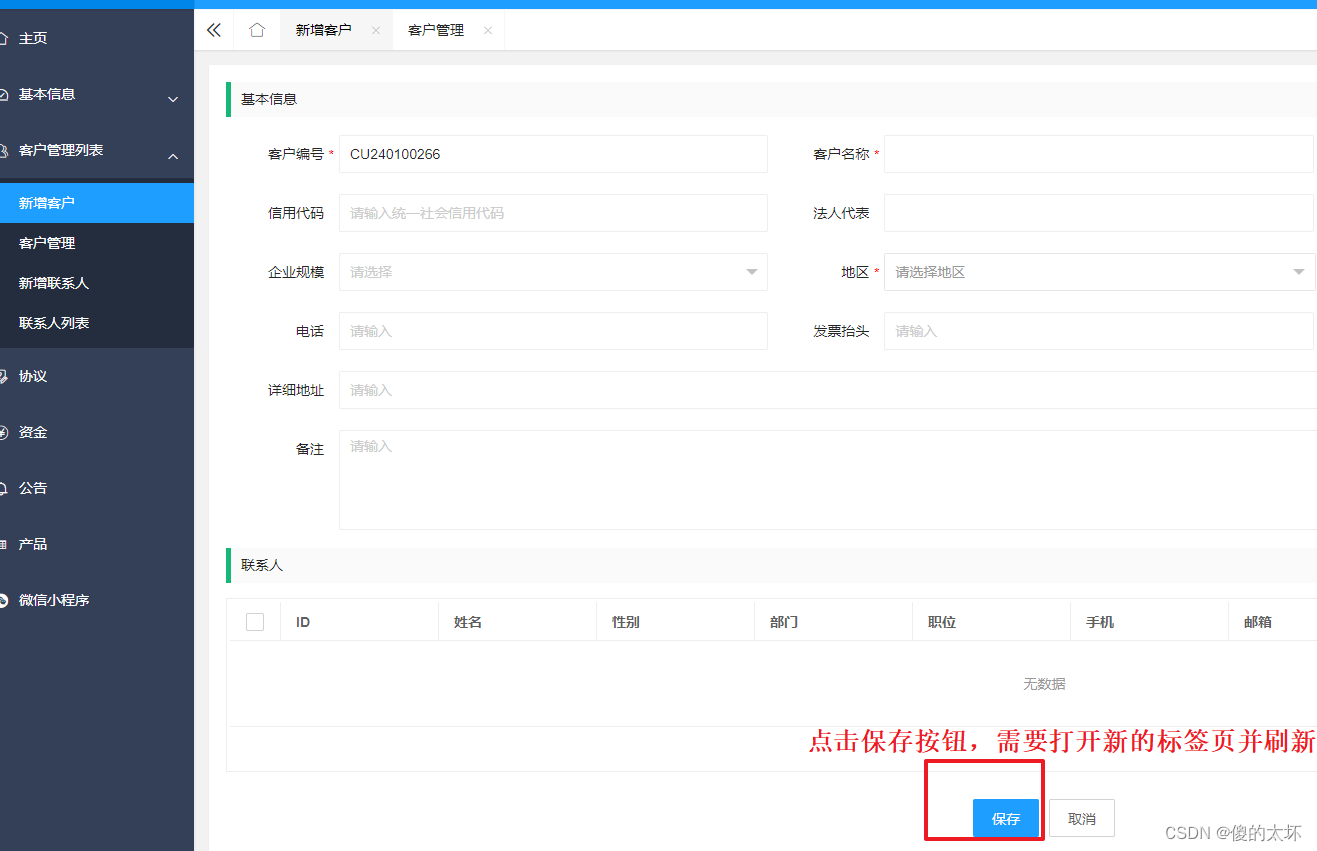
layuiadmin新建tabs标签页,点击保存,打开新的标签页并刷新
用的layuiamin前端框架 需求:新增的页面为一个标签页,保存后,需要刷新列表 1、新建customMethod.js文件,自定义自己的方法 layui.define(function (exports) {var $ layui.$var customMethod {// 表单点击保存后,…...

Rxjs概念 学习
RxJS 是一个流式编程库,用于处理异步数据流和事件流。它基于观察者模式和迭代器模式,提供了丰富的操作符和工具,用于处理和操作数据流。RxJS 的核心概念包括可观察对象(Observable)、观察者(Observer&#…...
 --- 西北乱跑娃)
pillow像型学操作(转载笔记) --- 西北乱跑娃
Opencv、Matplotlib(plt)、Pillow(PIL)、Pytorch读取数据的通道顺序 需注意:Pillow加载图像后的尺寸是二维,图形化是三维,但无法打印三维尺寸。 详细区别: Opencv:uint8的ndarray数据,通道顺序[h, w, c],颜色通道BGR。 导入模块:import cv2 (1)cv2.imread() (2)cv…...
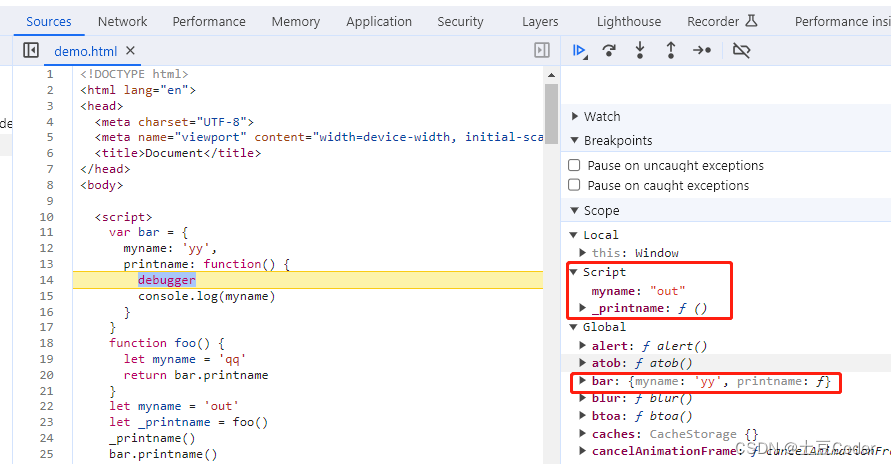
JS作用域链和闭包
JS作用域链和闭包 引题作用域链词法作用域闭包思考题 闭包如何回收 引题 有没有人跟我一样,面试中要是问基础,最怕遇到的就是闭包问题,闭包在 JavaScript 中几乎无处不在,理解作用域链是理解闭包的基础,同时作用域链和…...

【Spring实战】15 Logback
文章目录 1. 依赖2. 配置3. 打印日志4. 启动程序5. 验证6. 调整日志级别7. 代码详细总结 Spring 作为一个现代化的 Java 开发框架,提供了很多便利的功能,其中包括灵活而强大的日志记录。本文将介绍如何结合 Spring 和 Logback 配置和使用日志,…...
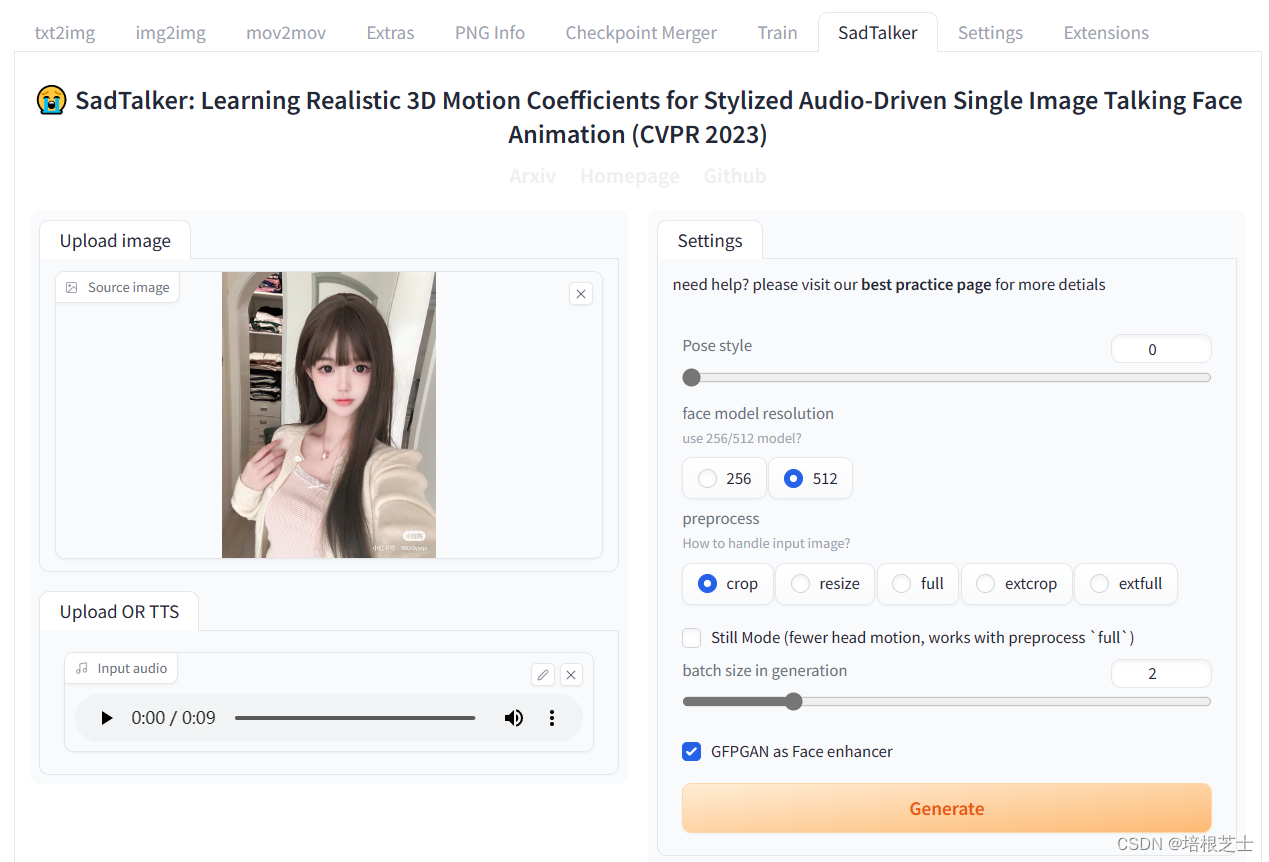
Stable Diffusion WebUI安装合成面部说话插件SadTalker
SadTalker可以根据一张图片、一段音频,合成面部说这段语音的视频。图片需要真人或者接近真人。 安装ffmpeg 下载地址: https://www.gyan.dev/ffmpeg/builds/ 下载ffmpeg-git-full.7z 后解压,将解压后的目录\bin添加到环境变量的Path中。 在…...

CSS 纵向顶部往下动画
<template><div class"container" mouseenter"startAnimation" mouseleave"stopAnimation"><!-- 旋方块 --><div class"box" :class"{ scale-up-ver-top: isAnimating }"><!-- 元素内容 -->&…...

科普:敏捷估算为什么用斐波那契数列
被一个同学问:敏捷估算为什么用斐波那契数列?有什么意义? 简单说说我自己的简介: 敏捷开发中使用斐波那契数列来估算的原因是,斐波那契数列可以用于估算任务的难度级别,并帮助团队预测完成任务所需的时间…...
HarmonyOS资源分类与访问
资源分类与访问 应用开发过程中,经常需要用到颜色、字体、间距、图片等资源,在不同的设备或配置中,这些资源的值可能不同。 应用资源:借助资源文件能力,开发者在应用中自定义资源,自行管理这些资源在不同…...

message: 没有找到可以构建的 NPM 包,请确认需要参与构建的 npm 都在 `miniprogra
第一步:修改 project.config.json 文件 "packNpmRelationList": [{"packageJsonPath": "./package.json","miniprogramNpmDistDir": "./miniprogram/"}], "packNpmManually": true 第二步:…...
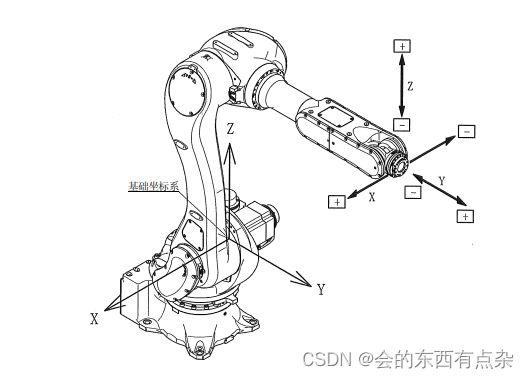
基于C#的机械臂欧拉角与旋转矩阵转换
欧拉角概述 机器人末端执行器姿态描述方法主要有四种:旋转矩阵法、欧拉角法、等效轴角法和四元数法。所以,欧拉角是描述机械臂末端姿态的重要方法之一。 关于欧拉角的历史,由来已久,莱昂哈德欧拉用欧拉角来描述刚体在三维欧几里…...

【百度前端三面面试题】
在某乎看到的《百度前端三面面试题全部公开,三面的最后一个问题令我窒息》 其中下面三个问题没有给出答案,我虽然是前端出身,但也面试过一些人,大概分析一下这些问题。 面试中问这几个问题的目的是什么 ,怎么回答 上…...

【Java面试题】HTTP与 HTTPS 的区别
HTTP 与 HTTPS 的区别 : 主要体现在三个方面,分别是 信息传输安全、证书和身份验证 、连接方式 信息传输安全: HTTP 是超文本传输协议,HTTP下的信息是明文传输的,因此使用HTTP协议可能导致信息被截获或者第三方恶意…...

vue3 v-model语法糖
vue2 中父子组件数据同步 父→子 子→父 如何实现? v-model“count” 或者 xxx.sync“msg” v-model 语法糖 完整写法 :value“count” 和 input“count$event” xxx.sync 语法糖 完整写法 :xxx“msg” 和 update:xxx“msg$event” 现在:一个 v-mo…...
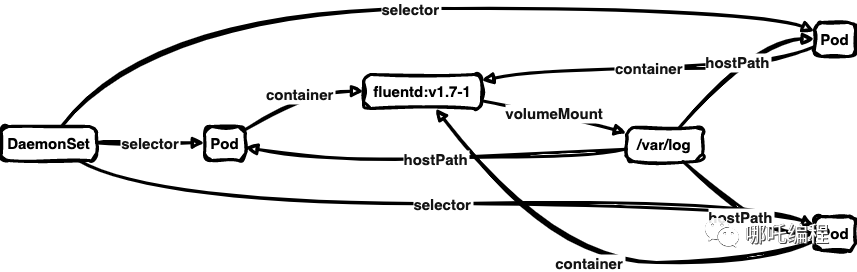
【k8s】deamonset文件和说明
目录 deamonset的相关命令 deamonset的定义 deamonset的使用场景 deamonset的例子 deamonset字段说明 serviceAccountName DaemonSet的结构及其各个部分的作用 deamonset的相关命令 #查看<name-space>空间内有哪些deamonset kubectl get DaemonSet -n <na…...
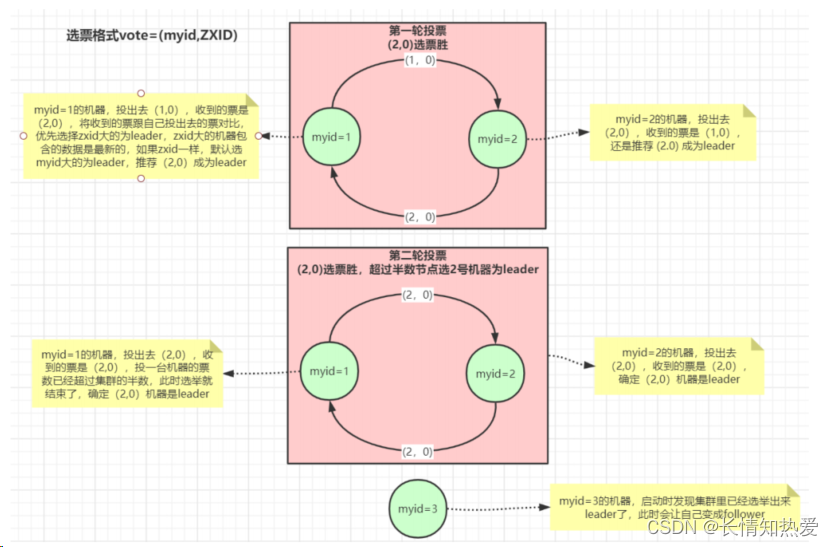
Zookeeper-Zookeeper特性与节点数据类型详解
1.Zookeeper介绍 ZooKeeper 是一个开源的分布式协调框架,是Apache Hadoop 的一个子项目,主要用来解决分布式集群中应用系统的一致性问题。Zookeeper 的设计目标是将那些复杂目容易出错的分布式一致性服务封装起来,构成一高效可靠的原语集&…...
云计算复习提纲
第一章 大数据的概念:海量数据的规模巨大到无法通过目前主流的计算机系统在合理时间内获取、存储、管理、处理并提炼以帮助使用者决策 大数据的特点:①数据量大,存储的数据量巨大,PB级别是常态;②多样,数…...
Vue-响应式数据
一、ref创建基本类型的响应式数据 vue3可以使用ref、reactive去定义响应式数数据。 知识点汇总 使用ref需要先引入ref,import {ref} from vue在模板 template 中使用了添加ref 的响应式数据,变量的后面不用添加.value所有js代码里面,去操作r…...

Vue开发者必备!手把手教你实现类似Element Plus的全局提示组件!
前言 在Web开发中,用户体验至关重要。有效的信息提示和错误消息对于确保用户更好地理解和操作至关重要。在这个背景下,全局弹框提示组件成为了一个非常有用的工具。Vue.js,作为当前最受欢迎的前端框架之一,为创建灵活、可复用的弹…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
