kotlin foreach 循环
java中的foreach循环也使用于kotlin ,先回顾下java里面的foreach循环
java foreach循环格式
for(元素类型t 元素变量x : 遍历对象obj){引用了x的语句;}例如:
int[] intary = {1,2,3,4};for (int a: intary) {Log.d("=======intary", String.valueOf(a));}kotlin中 这些都帮我们下写好了,下面是源码
/**
* Performs the given [action] on each element.
*/
public inline fun IntArray.forEach(action: (Int) -> Unit): Unit {
for (element in this) action(element)
}
使用的时候直接是要遍历的对象.foreach 即可
下面就是kotlin foreach循环的一个简单的遍历
val intary = intArrayOf(1, 2, 3, 4)intary.forEach {Log.d("=======intary", it.toString())}相关文章:

kotlin foreach 循环
java中的foreach循环也使用于kotlin ,先回顾下java里面的foreach循环 java foreach循环格式 for(元素类型t 元素变量x : 遍历对象obj){引用了x的语句;} 例如: int[] intary {1,2,3,4};for (int a: intary) {Log.d("intary", String.value…...

分享相关知识
直接使用海龟图进行创作移动动态的游戏 这段代码是一个简单的turtle模块实现的小游戏,主要功能包括: 窗口和无人机初始化: 创建了一个turtle窗口,设置了窗口的背景颜色和标题。创建了一个表示无人机的turtle,形状为正…...
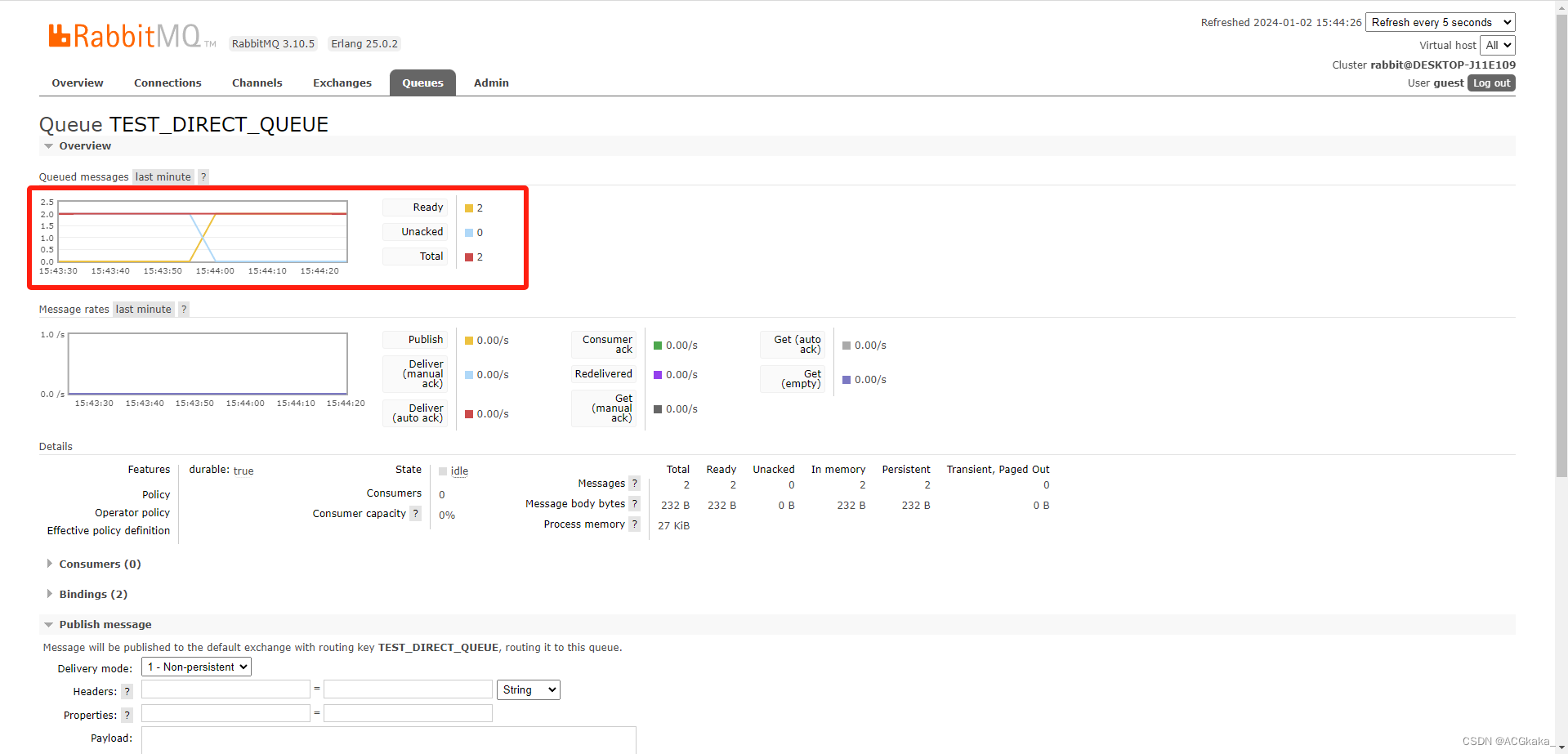
RabbitMQ(七)ACK 消息确认机制
目录 一、简介1.1 背景1.2 定义1.3 如何查看确认/未确认的消息数? 二、消息确认机制的分类2.1 消息发送确认1)ConfirmCallback方法2)ReturnCallback方法3)代码实现方式一:统一配置a.配置类a.生产者c.消费者d.测试结果 …...

ubuntu 编译内核报错
Ubuntu 编译 Linux 内核经常会遇到如下错误: 如果报错 canonical-certs.pem: 如下: make[1]: *** No rule to make target ‘debian/canonical-certs.pem’, needed by ‘certs/x509_certificate_list’. Stop. make: *** [Makefile:1868: …...

Python之自然语言处理库snowNLP
一、介绍 SnowNLP是一个python写的类库,可以方便的处理中文文本内容,是受到了TextBlob的启发而写的,由于现在大部分的自然语言处理库基本都是针对英文的,于是写了一个方便处理中文的类库,并且和TextBlob不同的是&…...
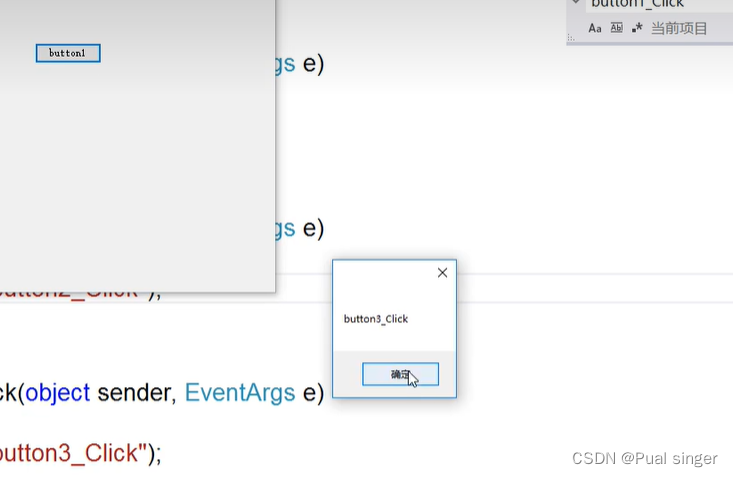
C# 语法进阶 委托
1.委托 委托是一个引用类型,其实他是一个类,保存方法的指针 (指针:保存一个变量的地址)他指向一个方法,当我们调用委托的时候这个方法就立即被执行 关键字:delegate 运行结果: 思…...
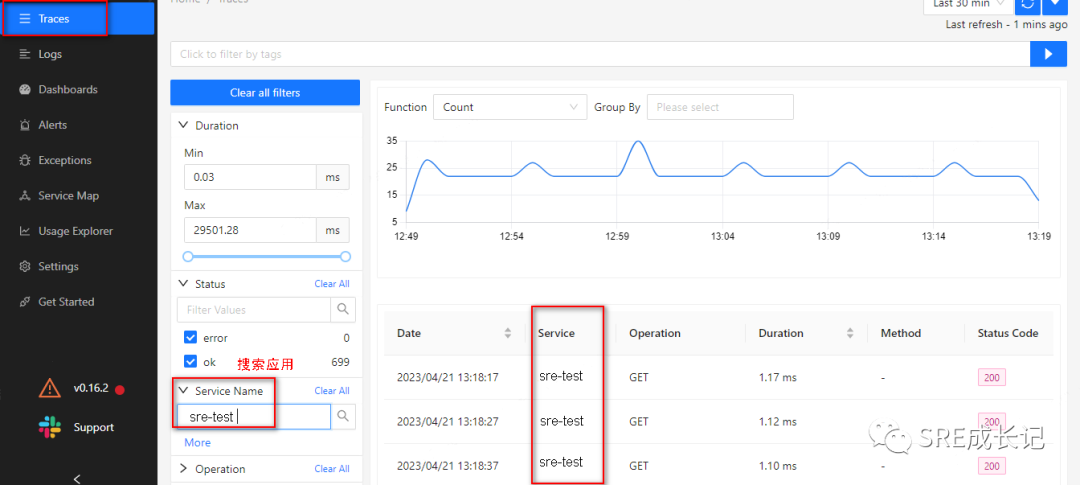
开源可观测性平台Signoz(四)【链路监控及数据库中间件监控篇】
转载说明:如果您喜欢这篇文章并打算转载它,请私信作者取得授权。感谢您喜爱本文,请文明转载,谢谢。 前文链接: 开源可观测性平台Signoz系列(一)【开篇】 开源可观测性平台Signoz&…...

【嵌入式开发 Linux 常用命令系列 4.2 -- git .gitignore 使用详细介绍】
文章目录 .gitignore 使用详细介绍.gitignore 文件的位置.gitignore 语法规则使用示例注意事项 .gitignore 使用详细介绍 .gitignore 文件是一个特殊的文本文件,它告诉 Git 哪些文件或目录是可以被忽略的,即不应该被纳入版本控制系统。这主要用于避免一…...

【熔断限流组件resilience4j和hystrix】
文章目录 🔊博主介绍🥤本文内容起因resilience4j落地实现pom.xml依赖application.yml配置接口使用 hystrix 落地实现pom.xml依赖启动类上添加注解接口上使用 📢文章总结📥博主目标 🔊博主介绍 🌟我是廖志伟…...
微服务雪崩问题及解决方案
雪崩问题 微服务中,服务间调用关系错综复杂,一个微服务往往依赖于多个其它微服务。 微服务之间相互调用,因为调用链中的一个服务故障,引起整个链路都无法访问的情况。 如果服务提供者A发生了故障,当前的应用的部分业务…...

008、所有权
所有权可以说是Rust中最为独特的一个功能了。正是所有权概念和相关工具的引入,Rust才能够在没有垃圾回收机制的前提下保障内存安全。 因此,正确地了解所有权概念及其在Rust中的实现方式,对于所有Rust开发者来讲都是十分重要的。在本文中&…...

千里马2023年终总结-android framework实战
背景: hi粉丝朋友们: 2023年马上就过去了,很多学员朋友也都希望马哥这边写个年终总结,因为这几个月时间都忙于新课程halsystracesurfaceflinger专题的开发,差点都忘记了这个事情了,今天特别花时间来写个bl…...

vue3中pinia的使用及持久化(详细解释)
解释一下pinia: Pinia是一个基于Vue3的状态管理库,它提供了类似Vuex的功能,但是更加轻量化和简单易用。Pinia的核心思想是将所有状态存储在单个store中,并且将store的行为和数据暴露为可响应的API,从而实现数据&#…...

安装 yarn、pnpm、功能比较
安装 yarn 官网:https://classic.yarnpkg.com/ 快速、可靠和安全的依赖性管理。 Yarn是您代码的软件包管理器。它允许您使用和共享(例如JavaScript)与来自世界各地的其他开发人员一起编写代码。Yarn是一个新的快速安全可信赖的可以替代 NP…...

计算机专业个人简历范文(8篇)
HR浏览一份简历也就25秒左右,如果你连「好简历」都没有,怎么能找到好工作呢? 如果你不懂得如何在简历上展示自己,或者觉得怎么改简历都不出彩,那请你一定仔细读完。 互联网运营个人简历范文> 男 22 本科 AI简历…...

几个实用网站
论文短语:https://www.phrasebank.manchester.ac.uk/ 翻译:https://www.deepl.com/en/translator 润色:https://quillbot.com/ 榜单:www.paperwithcode.com ****NLP民工的乐园: 几乎最全的中文NLP资源库:****https…...

Pycharm 切换interpreter---python的环境和第三方库问题
这篇回答两个问题: 1.为什么在 pycharm中打开新的project,切换interpreter 之后发现自己之前装的库消失了? 2.为什么 interpreter 切换到python3.8了, terminal 还是在 3.9?? 问题的关键:搞懂什…...

TP-LINK 路由器忘记密码 - 恢复出厂设置
TP-LINK 路由器忘记密码 - 恢复出厂设置 1. 恢复出厂设置2. 创建管理员密码3. 上网设置4. 无线设置5. TP-LINK ID6. 网络状态References 1. 恢复出厂设置 在设备通电的情况下,按住路由器背面的 Reset 按钮直到所有指示灯同时亮起后松开。 2. 创建管理员密码 3. 上网…...

关闭 Elasticsearch 集群的安全性设置
关闭 Elasticsearch 集群的安全性设置,特别是如果您正在使用 X-Pack,涉及到修改 Elasticsearch 的配置。以下是一般步骤,但请注意,这可能会使您的 Elasticsearch 集群面临安全风险,因此建议仅在开发或测试环境中执行此…...
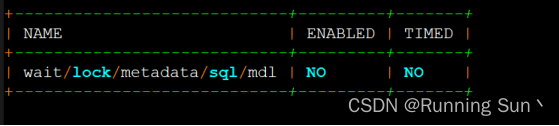
[技术分享]一招解决 MySQL 中 DDL 被阻塞的问题
爱可生开源社区. 爱可生开源社区,提供稳定的MySQL企业级开源工具及服务,每年1024开源一款优良组件,并持续运营维护。 背景 之前碰到客户咨询定位DDL阻塞的相关问题,整理了一下方法,如何解决DDL被阻塞的问题。下面,就这个问题,整理了一下思路: 怎么判断一个 DDL 是…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
