红黑树(Insert())
文章目录
- 红黑树
- 代码
- 红黑树性质
- 红黑树vsAVL树
- 红黑树的实现
- Insert()
- 情况一:如果我插入的新节点时红色的
- 情况二:叔叔是黑色或者不存在
- 情况三: cur红,p为红,g为黑,u不存在或者为黑-双旋
- 检查
- erase()
- 红黑树vsAVL树
- 红黑树的应用:
红黑树
二叉搜索树
代码
红黑树性质
- 每个节点不是黑色就是红色.
- 根节点是黑色
- 红色节点的孩子节点都是黑色的,所以不存在连续的红色.
- 对于节点,从该节点到所有后代叶子节点的简单路径上,包含相同数目的黑色节点。
- 这里的路径不是到叶子结点中止,而是到NULL。
- 节点个数,最长路径不超过最短路径的2倍。最短路径是全黑,最长路径就是一黑一红。假设每条路径黑节点的数量是N,N<=任意路径长度<=2N
- 每个叶子节点都是黑色的,这时候的叶子结点是NULL不是平常的叶子结点。在数路径的时候看的不是叶子结点而是NULL的个数,来保证每条路径黑色节点的数目是相等的.
红黑树vsAVL树
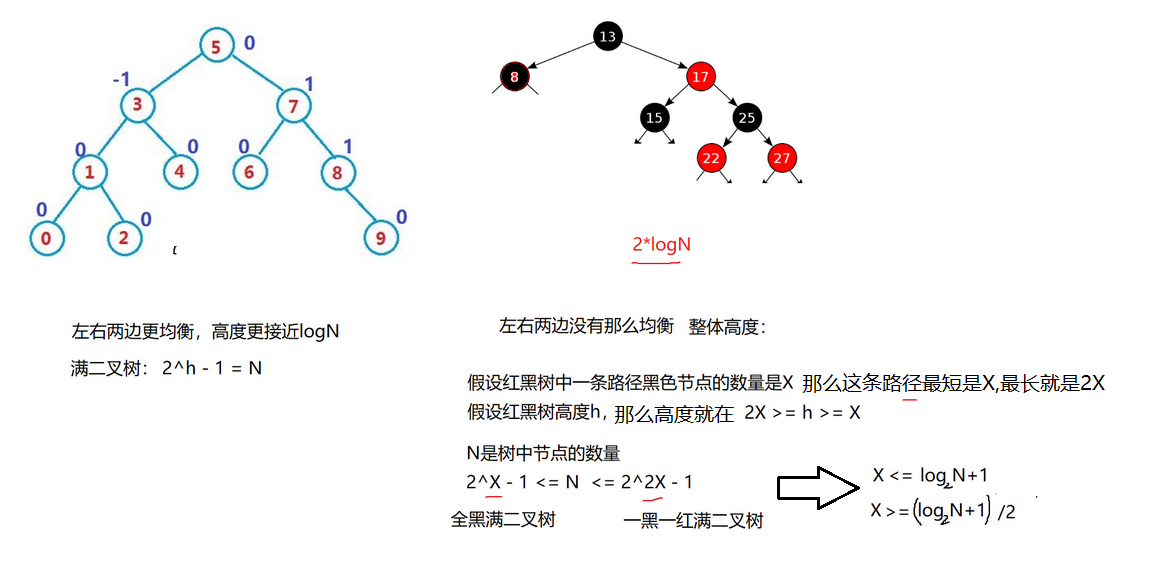
AVL树是严格平衡树的左右相差不超过2,AVL左右两端更加均衡,高度更接近logN。红黑树是近似平衡,红黑树两边最坏情况是2logN。AVL树效率更高.
内存中搜索是差不多的,logN足够小,CPU对于这种很小基数的2倍是很快的,几乎无差别,假设是10亿个数,AVL树放30层,红黑树可能是60层,查找30次和60次对于CPU很小.但是AVL是旋转了很多次,红黑树是不一定旋转的。所以综合来说红黑树更优.
红黑树的实现
Insert()
-
第一次插入是插入那个节点好?
插入黑节点或者红结点就是在违反规则,所以需要考虑那个代价更小,所以选择红结点。
-
如果增加叶子结点是黑节点,那么别的路径的黑节点个数怎么平衡?影响太大。
-
如果插入的是红色,可能父亲是黑色,就没问题;如果父亲是红色就不行,这两种存在概率问题,有空可钻.
-
情况一:如果我插入的新节点时红色的
父节点是红的,祖父一定是黑的,(没有连续的红结点),所以看叔叔节点,如果是红结点,那么只需要将parent和uncle节点都改为黑色,祖父g变成红色(因为祖父不一定是根节点,所以我要保证所有路径黑节点个数相同)
如果g->parent是红色的,就需要cur=g,将祖父当成新增,继续向上调整。如果g-parent是黑色就可以结束了。所以就存在cur可能不是新增节点了,是某一个新增节点的祖父.
- 所以cur可能是新增,也有可能是新增的祖父节点的n次。
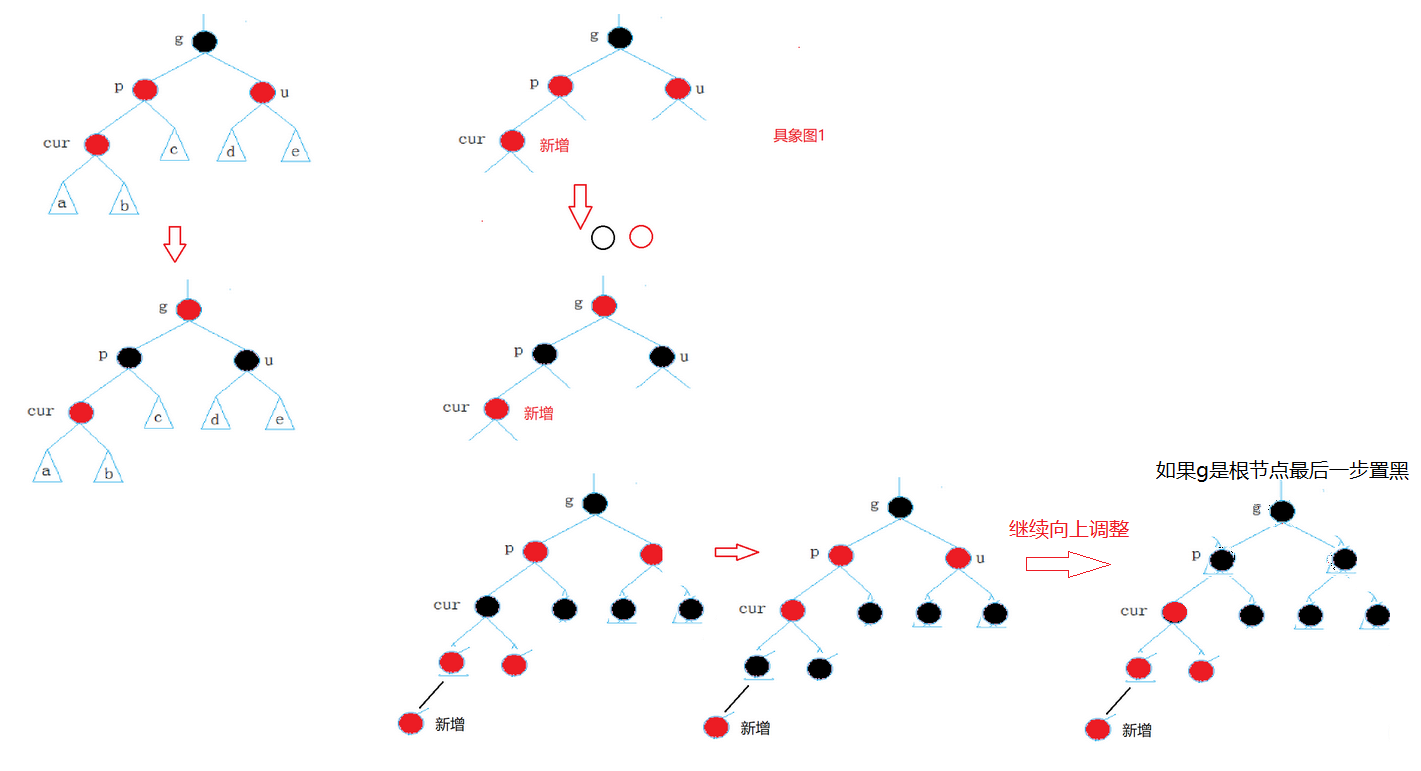
情况二:叔叔是黑色或者不存在
单纯变色不行了,因为最长路径已经超过了最短路径的2倍,就需要旋转一下.旋转的目的就是保持搜索树降低他的高度,让他左右均衡.所以是旋转加变色,先根节点变黑。旋转又分为左右单旋和双旋的情况
- 右单旋图示(左单旋同理)
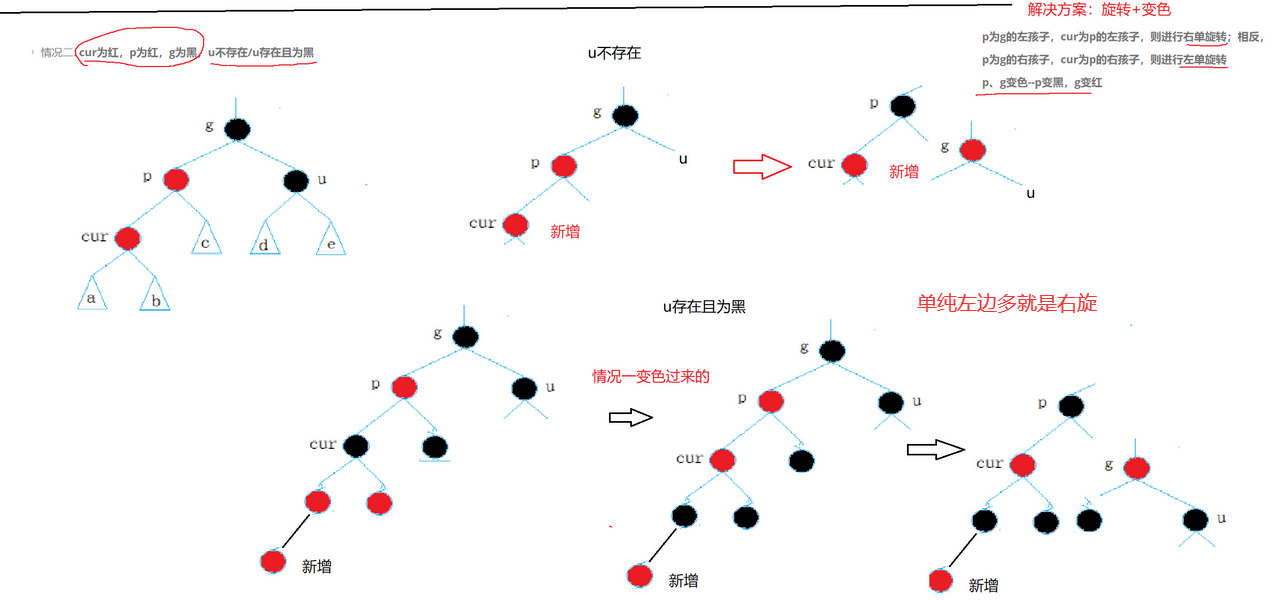
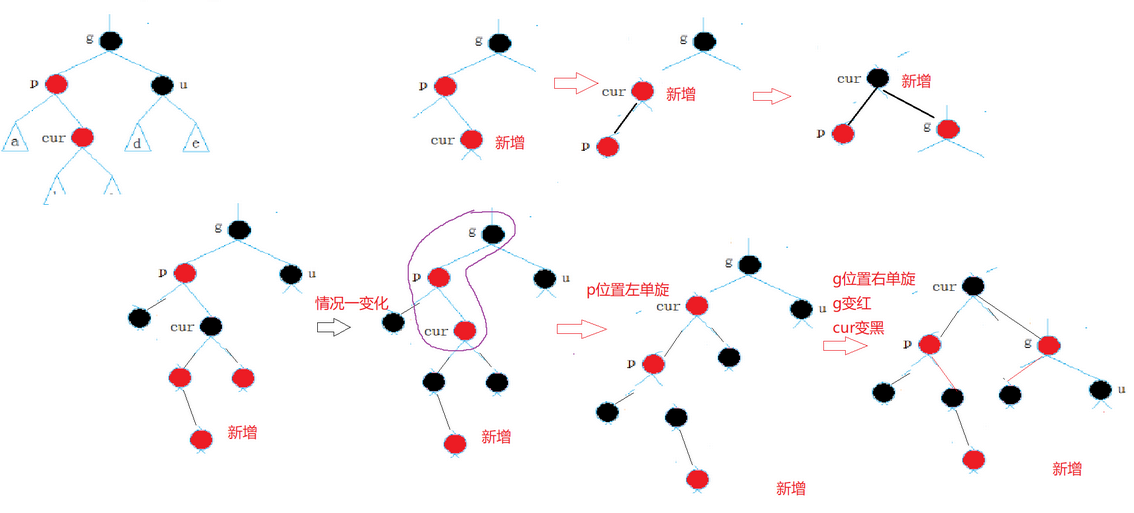
情况三: cur红,p为红,g为黑,u不存在或者为黑-双旋
折线,走单旋是没有效果的,只是把左边高变为右边高.所以走双旋.
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转,然后针对g做右单旋
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转.然后针对g做左单旋
检查
完成之后,编译执行正确只能保证这是一棵搜索树,对于红黑树还需要进一步检验。
- 根节点的颜色必须是黑色
- 如果节点是红色,直接验证他的父亲是不是红色,验证孩子的可能性太多
- 前序遍历就是深度优先遍历,路径中统计黑节点个数就行,给定参考值
banchmark某一条路径的比如最左路径,遍历一条路径,就将这条路径的值blackNum和基准值比较一次,看看每条路径的黑节点个数是否相等.
bool IsBalance(){if (_root && _root->_color == RED){cout << "根节点不是黑色" << endl;return false;}int banchmark = 0;Node* left = _root;while (left){if (left->_color == BLACK){++banchmark;}left = left->_left;}int blackNum = 0;return _IsBalance(_root, banchmark, blackNum);}
bool _IsBalance(Node* root, int banchmark, int blackNum){if (root == nullptr){if (banchmark != blackNum){cout << "存在路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_color == RED && root->_parent->_color == RED){cout << "连续出现红色节点" << endl;return false;}if (root->_color == BLACK){++blackNum;}return _IsBalance(root->_left, banchmark, blackNum)&& _IsBalance(root->_right, banchmark, blackNum)}
erase()
大佬博客
红黑树vsAVL树
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O(logN),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多.
红黑树的应用:
- C++ STL库 – map/set、mutil_map/mutil_set
- Java 库
- linux内核
- 其他一些库
相关文章:

红黑树(Insert())
文章目录红黑树代码红黑树性质红黑树vsAVL树红黑树的实现Insert()情况一:如果我插入的新节点时红色的情况二:叔叔是黑色或者不存在情况三: cur红,p为红,g为黑,u不存在或者为黑-双旋检查erase()红黑树vsAVL树红黑树的应用:红黑树 二叉搜索树 …...

MOV指令使用
mov用于数据传送。之后分为目的操作数和源操作数,目的操作数必须是通用寄存器或者内存单元:源操作数可以是具有相同数据宽度的通用寄存器或者内存单元,还可以是立即数。传送指令只影响目的操作数内容,不改变源操作数内容。 如&am…...

解释一下RecyclerView的适配器内部方法
RecyclerView的适配器(Adapter) 是一个连接数据模型和RecyclerView的桥梁,它在RecyclerView中提供了数据和布局之间的连接。下面是RecyclerView适配器中常用的几个方法的解释: 1.onCreateViewHolder(ViewGroup parent, int view…...

集合框架及背后的数据结构
1.介绍: Java 集合框架,又被称为容器是定义在 java.util 包下的一组接口 interfaces 和其实现类 classes 。 其主要表现为将多个元素置于一个单元中,用于对这些元素进行快速、便捷的存储、检索 、管理 ,即平时我们俗称的增删查改…...
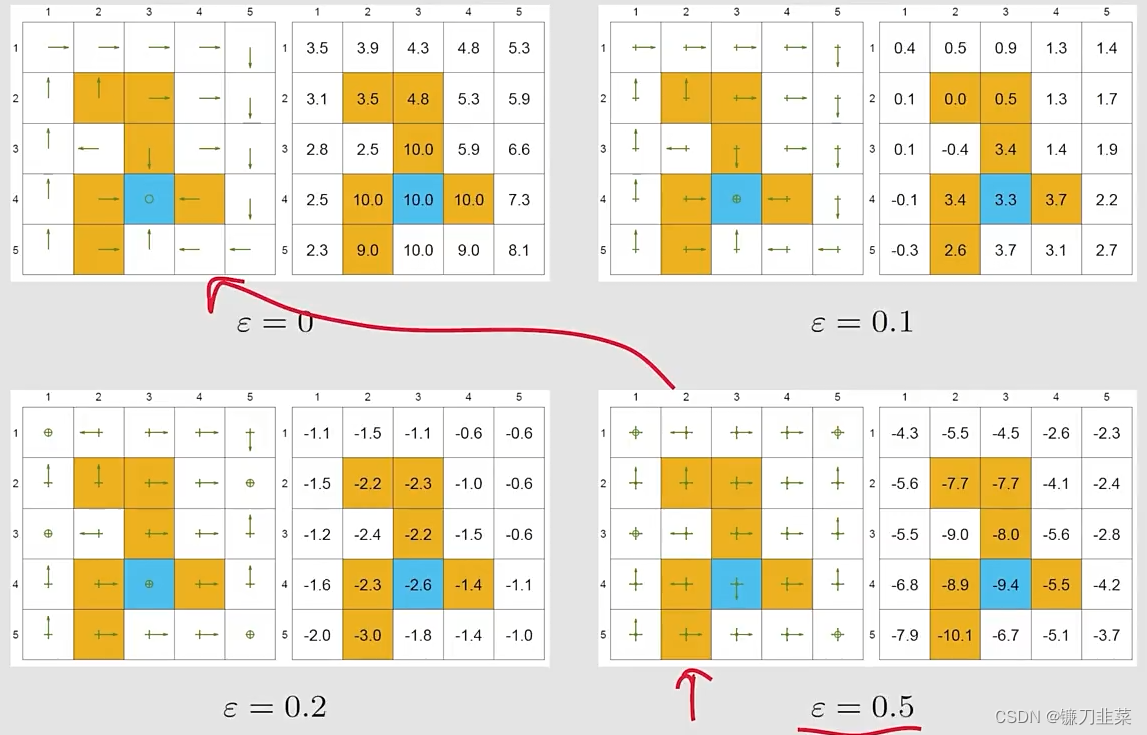
【强化学习】强化学习数学基础:蒙特卡洛方法
强化学习数学方法:蒙特卡洛方法举个例子举个例子1:投掷硬币The simplest MC-based RL algorithm举个例子2:Episode lengthUse data more efficientlyMC without exploring starts总结内容来源将value iteration和policy iteration方法称为mod…...

BI分析工具软件有哪些
最近发现很多人讨论BI数据分析,今天给大家全面介绍下BI数据分析相关的信息。首先给大家科普一下,什么是BI分析。 BI分析其实是指通过BI分析工具,对企业内部和外部的大量数据进行收集、整理、处理和分析,以提供有价值的洞察&#x…...

2023爱分析·RPA软件市场厂商评估报告:容智信息
目录 1. 研究范围定义 2. RPA软件市场分析 3. 厂商评估:容智信息 4. 入选证书 1. 研究范围定义 RPA即Robotic Process Automation(机器人流程自动化),是一种通过模拟人与软件系统的交互过程,实现由软件机器人…...
——里氏替换原则、依赖倒转原则)
设计模式之七大原则(二)——里氏替换原则、依赖倒转原则
1.里氏替换原则 里氏替换原则(Liskov Substitution Principle,LSP)由麻省理工学院计算机科学实验室的里斯科夫女士在 1987 年的“面向对象技术的高峰会议”(OOPSLA)上发表的一篇文章《数据抽象和层次》)里提…...
 | 2023年2月刊)
数据库日常实操优质文章分享(含Oracle、MySQL等) | 2023年2月刊
本文为大家整理了墨天轮数据社区2023年2月发布的优质技术文章,主题涵盖Oracle、MySQL、PostgreSQL等数据库的环境搭建、故障处理等日常实践操作,以及概念梳理、常用脚本等总结记录,分享给大家:Oracle优质技术文章概念梳理&基础…...

事件循环机制(Event Loop)和宏任务(macro-tast)微任务(micro-tast),详细讲解!!!
“事件循环机制” 和 “宏任务微任务” 也是前端面试中常考的面试题了。首先,要深刻理解这些概念的话,需要回顾一些知识点。知识点回顾1、进程与线程进程。 程序运行需要有它自己的专属内存空间,可以把这块内存空间简单的理解为进程每个应用至…...

mysql基础操作3
查询襄阳的员工姓名和性别,性别要求显示为 男 女SELECT ename,(CASE WHEN sexF THEN 女 ELSE 男 END)sexFROM empWHERE jiguan襄阳查询所有的订单,显示订单日期 订单数量 订单状态SELECT saleDate,salesQuantity,(CASE WHEN saleState1 THEN 新建 WHEN s…...

【Web安全】PHP安全
一、文件包含漏洞严格来说,文件包含就是代码注入的一种。代码注入,其原理就是注入一段用户能控制的脚本或代码并让服务器端执行。代码注入的典型代表就是文件包含。文件包含可能会出现在JSP、PHP、ASP等语言中,常见函数如下:PHP&a…...

双向链表+循环链表
循环链表双向链表 循环链表 循环链表是头尾相接的链表(即表中最后一个结点的指针域指向头结点,整个链表形成一个环)(circular linked list) **优点:**从表中任一结点出发均可访问全部结点 循环链表与单链表的主要差别当链表遍历时,判别当前…...
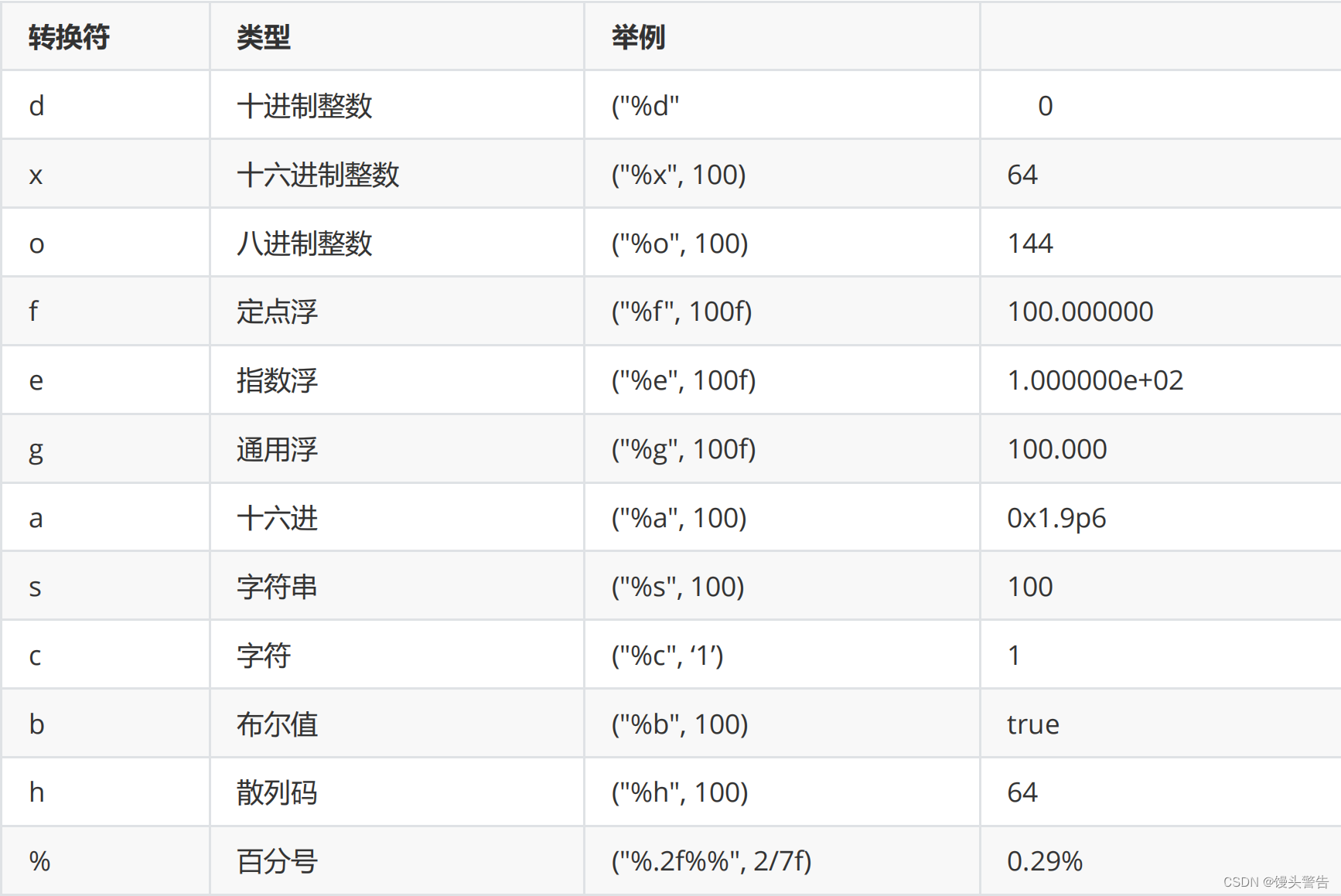
Java程序的逻辑控制
一、顺序结构 顺序结构比较简单,如果我们按照代码书写的顺序一行一行执行,将会是这样的: System.out.println("aaa"); System.out.println("bbb"); System.out.println("ccc"); // 运行结果 aaa bbb ccc 如…...

BUCTOJ - 2023上半年ACM蓝桥杯每周训练题-1-A~K题C++Python双语版
文章目录BUCTOJ - 2023上半年ACM&蓝桥杯每周训练题-1-A~K题CPython双语版前言问题 A: 1.2 神奇兔子数列题目描述输入输出解题思路AC代码CPython问题 B: 1.3 马克思手稿中的数学题题目描述输入输出解题思路AC代码CPython问题 C: 1.4 爱因斯坦的阶梯题目描述输入输出解题思路…...
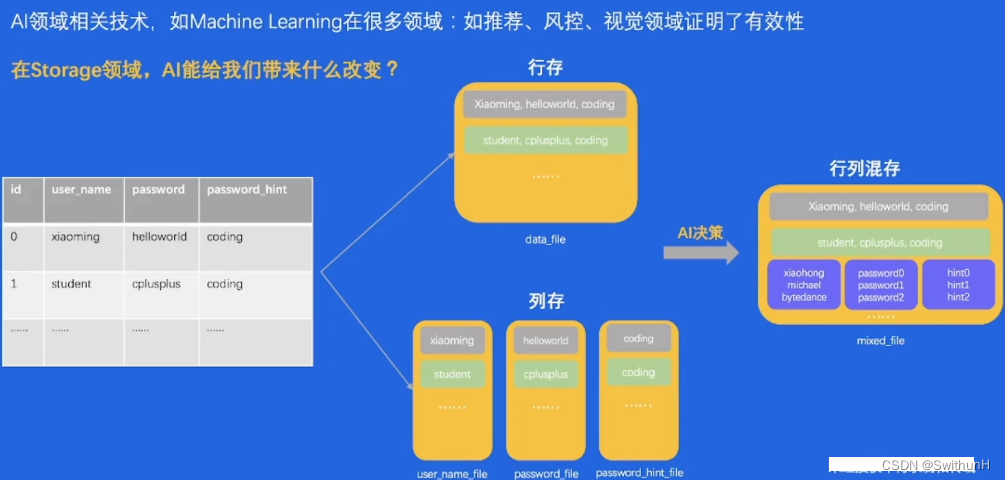
存储的本质-学习笔记
1 经典案例 1.1 数据的流动 一条用户注册数据流动到后端服务器,持久化保存到数据库中。 1.2 数据的持久化 校验数据的合法性修改内存写入存储介质2 存储&数据库简介 2.1 存储系统特点 性能敏感、容易受硬件影响、存储系统代码既“简单”又“复杂”。 2.2 数…...

新一代骨传导机皇重磅发布:南卡Neo骨传导运动耳机,性能全面提升
近日,中国最强骨传导品牌NANK南卡发布了最新一代骨传导耳机——南卡Neo骨传导耳机!该款耳机与运动专业性更强的南卡runner Pro4略微不同,其主要定位于轻运动风格,所以这款耳机的音质和佩戴舒适度达到了令人咂舌的地步!…...

Hbase Schema设计与数据模型操作
一、Hbase Schema设计 1,Schema 创建 使用 Apache HBase Shell 或使用 Java API 中的 Admin 来创建或更新 HBase 模式。 Configuration config HBaseConfiguration.create(); Admin admin new Admin(conf); TableName table TableName.valueOf("myTable&…...

微电影广告有哪些传播优势?
微电影广告是在基于微电影的模式下发展而来的,是伴随着当下快节奏、碎片化的生活方式而诞生的新兴广告表现形式。微电影广告凭借其具备的独特传播优势以及时代特征成为广大企业主塑造企业品牌形象的主要方式。那么,微电影广告究竟有哪些传播优势…...
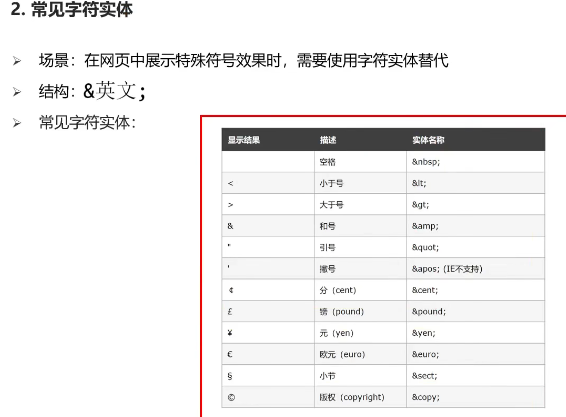
html基础(列表(ul、ol、dl)、表格table、表单(input、button、label)、div和span、空格nbsp)
1无序列表<ul>和有序列表<ol>1.1无序列表<ul><!-- 无序列表 --><ul><li>吃饭</li><li>睡觉</li><li>打豆豆</li></ul>1.2有序列表<ol><!-- 有序列表 --><ol><li>吃饭</li…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
