【算法经典题集】二分(持续更新~~~)
😽PREFACE
🎁欢迎各位→点赞👍 + 收藏⭐ + 评论📝
📢系列专栏:算法经典题集
🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用
💪种一棵树最好是十年前其次是现在
二分
整数二分
机器人跳跃问题
机器人正在玩一个古老的基于 DOS 的游戏。
游戏中有 N+1 座建筑——从 0 到 N 编号,从左到右排列。
编号为 0 的建筑高度为 0 个单位,编号为 ii 的建筑高度为 H(i) 个单位。
起初,机器人在编号为 0 的建筑处。
每一步,它跳到下一个(右边)建筑。
假设机器人在第 kk 个建筑,且它现在的能量值是 EE,下一步它将跳到第 k+1k+1 个建筑。
如果 H(k+1)>E,那么机器人就失去 H(k+1)−E 的能量值,否则它将得到 E−H(k+1)的能量值。
游戏目标是到达第 N 个建筑,在这个过程中能量值不能为负数个单位。
现在的问题是机器人至少以多少能量值开始游戏,才可以保证成功完成游戏?
输入格式
第一行输入整数 N。
第二行是 N 个空格分隔的整数,H(1),H(2),…,H(N)代表建筑物的高度。
输出格式
输出一个整数,表示所需的最少单位的初始能量值上取整后的结果。
数据范围
1≤N,H(i)≤10^5,
输入样例1:
5
3 4 3 2 4
输出样例1:
4
输入样例2:
3
4 4 4
输出样例2:
4
输入样例3:
3
1 6 4
输出样例3:
3
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int n, h[N];bool check(int e)
{for (int i = 1; i <= n; i++){e = e * 2 - h[i];if (e >= 1e5) return true;if (e < 0) return false;}return true;
}int main()
{cin >> n;for (int i = 1; i <= n; i++) cin >> h[i];int l = 0, r = 1e5;while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid;else l = mid + 1;}cout << r << endl;return 0;
}【注意点】
为什么该题可以用二分做呢? 因为题设条件满足单调性,并不是说二分就只能解决单调性,非单调性二分也能做
关于代码的11行是怎么来的,能否去掉?11行的由来是源于数学归纳法的证明,它有两个作用,一是加快代码运行速度,二是避免出现越界。如果把第十一行去掉的话,就要把e的类型改成double。
分巧克力
儿童节那天有 K 位小朋友到小明家做客。
小明拿出了珍藏的巧克力招待小朋友们。
小明一共有 N 块巧克力,其中第 i 块是 Hi×Wi 的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出 K 块巧克力分给小朋友们。
切出的巧克力需要满足:
形状是正方形,边长是整数
大小相同
例如一块 6×5 的巧克力可以切出 6 块 2×2的巧克力或者 2 块 3×3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小明计算出最大的边长是多少么?
输入格式
第一行包含两个整数 N 和 K。
以下 N 行每行包含两个整数 Hi 和 Wi。
输入保证每位小朋友至少能获得一块 1×1 的巧克力。
输出格式
输出切出的正方形巧克力最大可能的边长。
数据范围
1≤N,K≤10^5
1≤Hi,Wi≤10^5
输入样例:
2 10
6 5
5 6
输出样例:
2
分析:通过观察我们发现,巧克力最后分成的总块数k和边长x具有一定关系,当x越大,我们最终分得的小巧克力块数k就越小。边长的大小与最终分得的小巧克力块数k成反比关系。既然我们最终要求的答案x恰好和k有关,并且答案所在的区间又刚好可以由k一分为二成两种不同的性质,因此本道题可以使用二分,k就是我们要找的二分边界,左边的性质我们可以描述为cheak(x)≥k,也就是说左边区间内的边长所分得的小巧克力总块数要大于等于题目要求的块数,因此我们可以由此更新左端点,使得答案区间向右边缩小,这样不仅可以求得更大的边长x,也可以找到恰好满足题意的k。
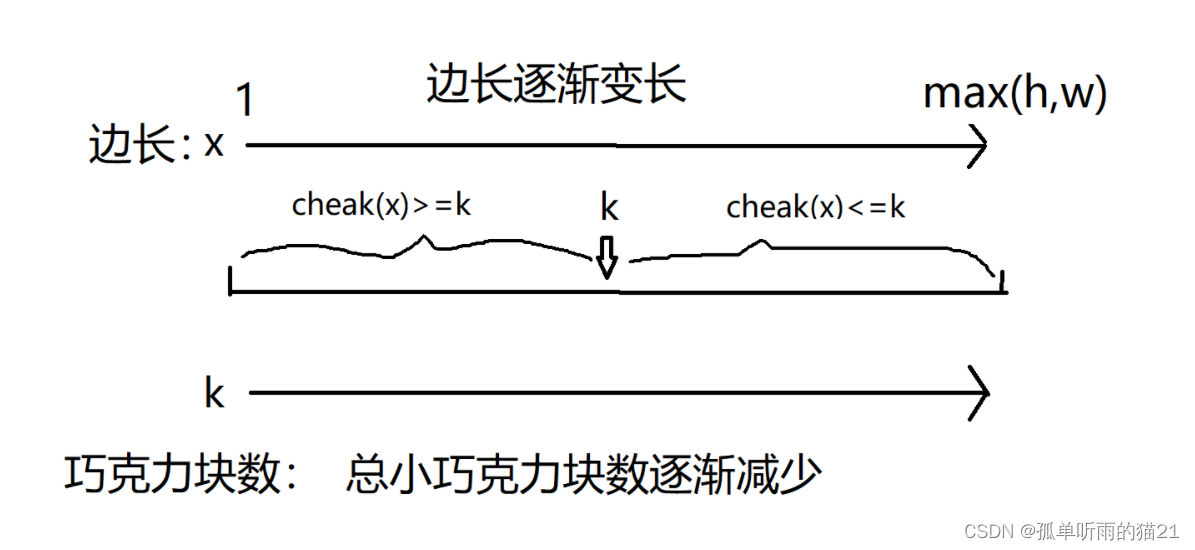
这样,我们的问题就得到了进一步简化,变成了如何设计cheak()函数,使得cheak(mid)可以刚好满足边界k的左边区间性质,这样我们便可以顺理成章的更新左端点,使得整个二分向右查找,最总找到我们所需要的答案x。
#include <iostream>
using namespace std;int const N = 100010;
int w[N], h[N];//存储长、宽
int n, k;bool check(int a)
{int num = 0;//记录分成长度为 a 的巧克力数量for (int i = 0; i < n; i++){num += (w[i] / a) * (h[i] / a);//每一大块可以分成的边长为 a 的巧克力数量if (num >= k) return true;//大于要求数量,返回真}return false;
}int main()
{cin >> n >> k;for (int i = 0; i < n; i++) cin >> h[i] >> w[i];int l = 1, r = 1e5;//小巧克力数量边长一定在 1 -- 100000 之间while (l < r)//二分小巧克力边长范围,找到符合要求的最大值{int mid = l + (r - l + 1 >> 1);//因为l = mid ,所以 mid 取 l + r + 1 >> 1,为了防止加和越界,改写成 l + (r - l + 1 >> 1)if (check(mid)) l = mid;else r = mid - 1;}cout << r << endl;return 0;
}跳石头

这是一道典型的二分套路题:“最小值最大化”,类似题还有“最大值最小化”。什么是“最小值最大化”呢?在所有可能的最小值中查找最大的那个值
#include <bits/stdc++.h>
using namespace std;
const int N =5e4+10;
int len,n,m;
int stone[N]; bool check(int d)//检查距离d是否合适
{int num,pos=0;//num记录搬走岩石的数量 for(int i=1;i<=n;i++)//当前站立的岩石 {if(stone[i]-pos<d) num++;//第i块岩石可以搬走 else pos=stone[i];//第i块岩石不能搬走 }if(num<=m) return true;//要移动的岩石比m少,满足条件 else return false;//要移动的岩石比m多,不满足条件
}int main()
{cin>>len>>n>>m;for(int i=1;i<=n;i++) cin>>stone[i];int l=0,r=len;while(l<r){int mid=l+r+1>>1;if(check(mid)) l=mid;//满足条件,说明mid小了,调大一点 else r=mid-1;//不满足条件,说明mid大了,调小一点 }cout<<r<<endl;return 0;
}实数二分
一元三次方程求解

暴力解法:
判断一个数是否为解的方法:如果函数值是连续变化的,且函数值在解的两边分别是大于0和小于0的,则解必然在它们中间。
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
double y(double x)
{return a*x*x*x+b*x*x+c*x+d;
} int main()
{cin>>a>>b>>c>>d;for(double i=-100;i<=100;i+=0.01){//写法一double j=i+0.01;double y1=y(i),y2=y(j);if(y1*y2<=0) printf("%.2lf ",(i+j)/2);//写法二if(abs(y(i))<1e-6) printf("%.2lf ",i);}return 0;
}二分:
#include <bits/stdc++.h>
using namespace std;
double a,b,c,d;
double y(double x)
{return a*x*x*x+b*x*x+c*x+d;
} int main()
{cin>>a>>b>>c>>d;for(int i=-100;i<100;i++)//题设条件给了两个根绝对值大于等于1,分200个小区间 {double left=i,right=i+1;//题设条件给了两个根绝对值大于等于1double y1=y(left),y2=y(right);if(y1==0) printf("%.2lf ",left);//判断左端点 if(y1*y2<0)//小区间内有根 {for(int j=0;j<100;j++)//在小区间内二分 {double mid=(left+right)/2;if(y(mid)*y(right)<=0)left=mid;elseright=mid;}printf("%.2lf ",right);} }return 0;
}相关文章:

【算法经典题集】二分(持续更新~~~)
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法经典题集🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用💪种一棵树最好是十年前其次是现在二分整数二分机器人…...
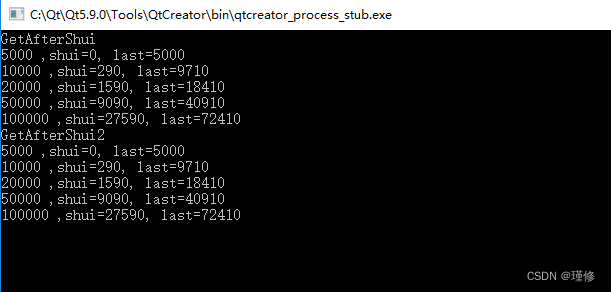
【c++】2023杭州月薪个税计算(chatGPT帮忙加注释)
参考信息 杭州市的个人所得税起征点是每月5000元。 个人所得税税率标准: 1、工资范围在1-5000元之间的,包括5000元,适用个人所得税税率为0%; 2、工资范围在5000-8000元之间的,包括8000元,适用个人所得税税率为3%; 3、工…...

【TypeScript】的上手学习指南!
目录TS简介TypeScript是什么?为什么要推荐使用TypeScript生态支持安装TypeScriptTS简介 TypeScript是什么? TypeScript官网 简介:TypeScript是JavaScript类型的超集,它可以编译成纯JavaScript。TypeScript可以在任何浏览器、任何计…...
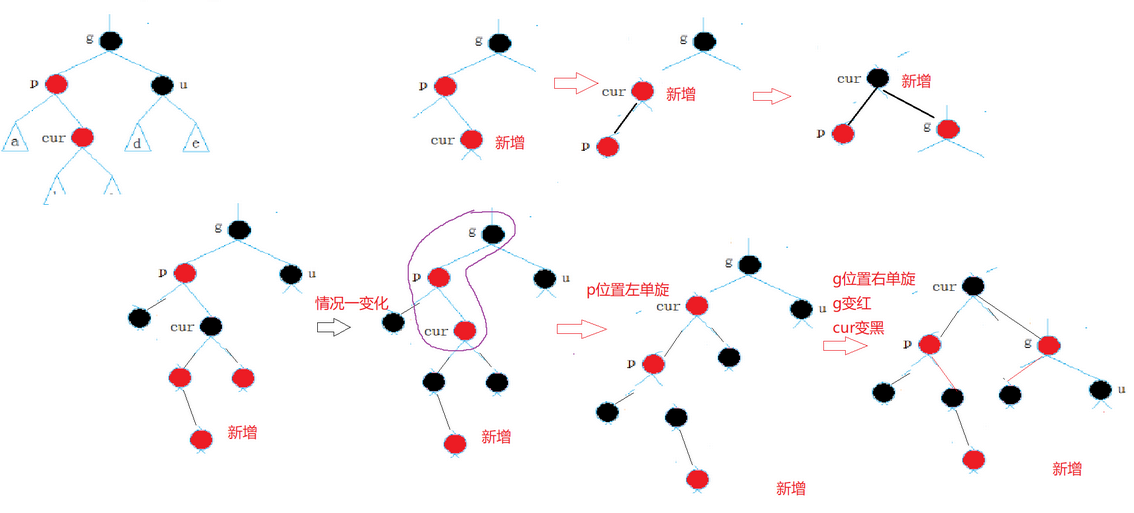
红黑树(Insert())
文章目录红黑树代码红黑树性质红黑树vsAVL树红黑树的实现Insert()情况一:如果我插入的新节点时红色的情况二:叔叔是黑色或者不存在情况三: cur红,p为红,g为黑,u不存在或者为黑-双旋检查erase()红黑树vsAVL树红黑树的应用:红黑树 二叉搜索树 …...

MOV指令使用
mov用于数据传送。之后分为目的操作数和源操作数,目的操作数必须是通用寄存器或者内存单元:源操作数可以是具有相同数据宽度的通用寄存器或者内存单元,还可以是立即数。传送指令只影响目的操作数内容,不改变源操作数内容。 如&am…...

解释一下RecyclerView的适配器内部方法
RecyclerView的适配器(Adapter) 是一个连接数据模型和RecyclerView的桥梁,它在RecyclerView中提供了数据和布局之间的连接。下面是RecyclerView适配器中常用的几个方法的解释: 1.onCreateViewHolder(ViewGroup parent, int view…...

集合框架及背后的数据结构
1.介绍: Java 集合框架,又被称为容器是定义在 java.util 包下的一组接口 interfaces 和其实现类 classes 。 其主要表现为将多个元素置于一个单元中,用于对这些元素进行快速、便捷的存储、检索 、管理 ,即平时我们俗称的增删查改…...
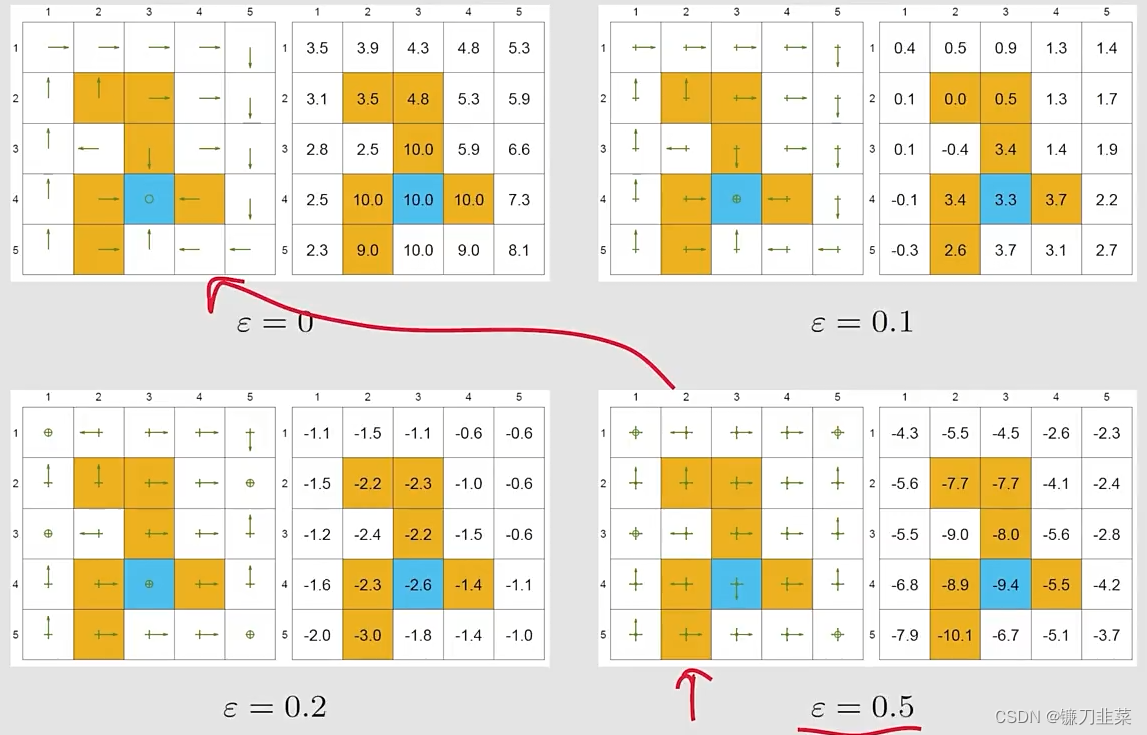
【强化学习】强化学习数学基础:蒙特卡洛方法
强化学习数学方法:蒙特卡洛方法举个例子举个例子1:投掷硬币The simplest MC-based RL algorithm举个例子2:Episode lengthUse data more efficientlyMC without exploring starts总结内容来源将value iteration和policy iteration方法称为mod…...

BI分析工具软件有哪些
最近发现很多人讨论BI数据分析,今天给大家全面介绍下BI数据分析相关的信息。首先给大家科普一下,什么是BI分析。 BI分析其实是指通过BI分析工具,对企业内部和外部的大量数据进行收集、整理、处理和分析,以提供有价值的洞察&#x…...

2023爱分析·RPA软件市场厂商评估报告:容智信息
目录 1. 研究范围定义 2. RPA软件市场分析 3. 厂商评估:容智信息 4. 入选证书 1. 研究范围定义 RPA即Robotic Process Automation(机器人流程自动化),是一种通过模拟人与软件系统的交互过程,实现由软件机器人…...
——里氏替换原则、依赖倒转原则)
设计模式之七大原则(二)——里氏替换原则、依赖倒转原则
1.里氏替换原则 里氏替换原则(Liskov Substitution Principle,LSP)由麻省理工学院计算机科学实验室的里斯科夫女士在 1987 年的“面向对象技术的高峰会议”(OOPSLA)上发表的一篇文章《数据抽象和层次》)里提…...
 | 2023年2月刊)
数据库日常实操优质文章分享(含Oracle、MySQL等) | 2023年2月刊
本文为大家整理了墨天轮数据社区2023年2月发布的优质技术文章,主题涵盖Oracle、MySQL、PostgreSQL等数据库的环境搭建、故障处理等日常实践操作,以及概念梳理、常用脚本等总结记录,分享给大家:Oracle优质技术文章概念梳理&基础…...

事件循环机制(Event Loop)和宏任务(macro-tast)微任务(micro-tast),详细讲解!!!
“事件循环机制” 和 “宏任务微任务” 也是前端面试中常考的面试题了。首先,要深刻理解这些概念的话,需要回顾一些知识点。知识点回顾1、进程与线程进程。 程序运行需要有它自己的专属内存空间,可以把这块内存空间简单的理解为进程每个应用至…...

mysql基础操作3
查询襄阳的员工姓名和性别,性别要求显示为 男 女SELECT ename,(CASE WHEN sexF THEN 女 ELSE 男 END)sexFROM empWHERE jiguan襄阳查询所有的订单,显示订单日期 订单数量 订单状态SELECT saleDate,salesQuantity,(CASE WHEN saleState1 THEN 新建 WHEN s…...

【Web安全】PHP安全
一、文件包含漏洞严格来说,文件包含就是代码注入的一种。代码注入,其原理就是注入一段用户能控制的脚本或代码并让服务器端执行。代码注入的典型代表就是文件包含。文件包含可能会出现在JSP、PHP、ASP等语言中,常见函数如下:PHP&a…...

双向链表+循环链表
循环链表双向链表 循环链表 循环链表是头尾相接的链表(即表中最后一个结点的指针域指向头结点,整个链表形成一个环)(circular linked list) **优点:**从表中任一结点出发均可访问全部结点 循环链表与单链表的主要差别当链表遍历时,判别当前…...
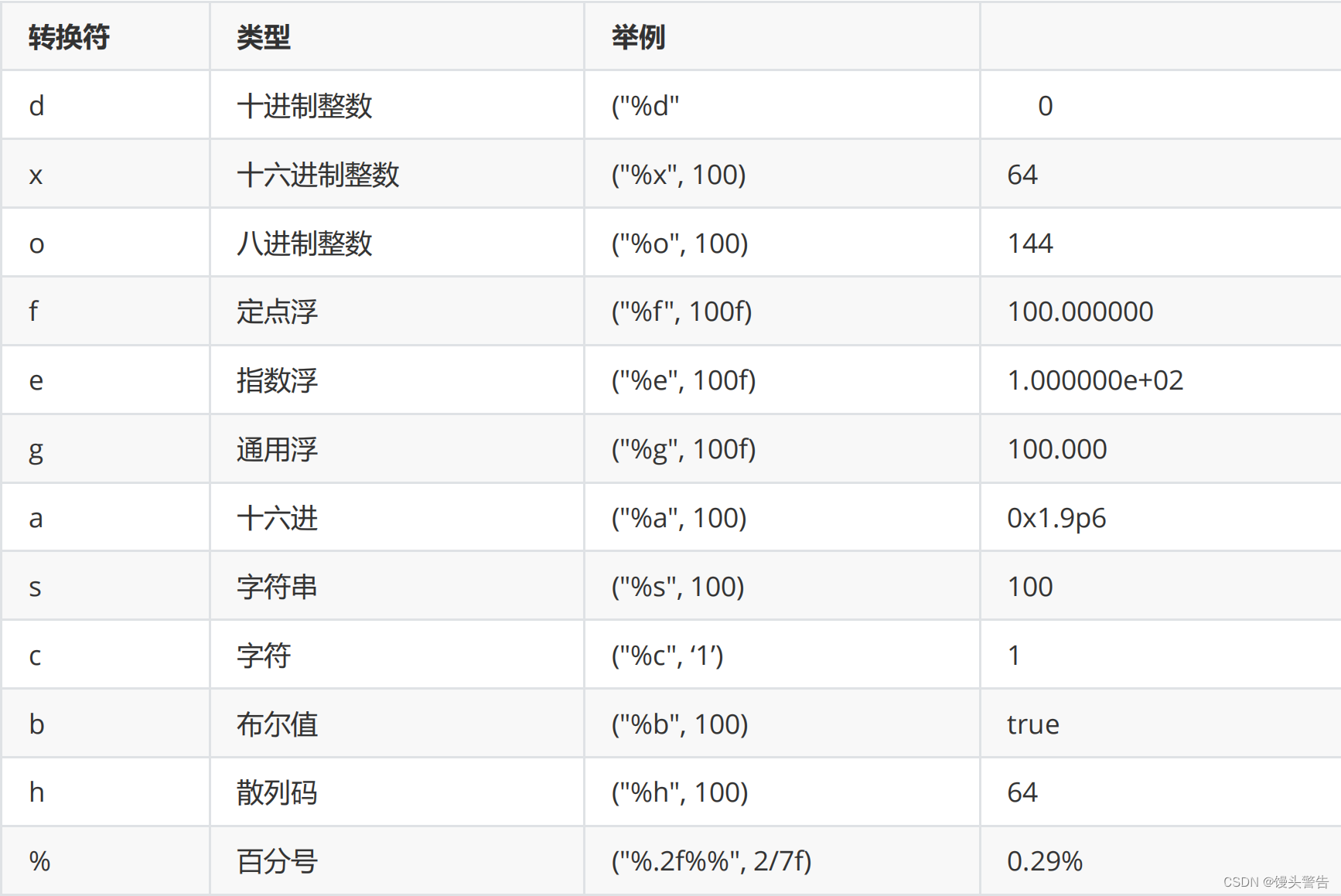
Java程序的逻辑控制
一、顺序结构 顺序结构比较简单,如果我们按照代码书写的顺序一行一行执行,将会是这样的: System.out.println("aaa"); System.out.println("bbb"); System.out.println("ccc"); // 运行结果 aaa bbb ccc 如…...

BUCTOJ - 2023上半年ACM蓝桥杯每周训练题-1-A~K题C++Python双语版
文章目录BUCTOJ - 2023上半年ACM&蓝桥杯每周训练题-1-A~K题CPython双语版前言问题 A: 1.2 神奇兔子数列题目描述输入输出解题思路AC代码CPython问题 B: 1.3 马克思手稿中的数学题题目描述输入输出解题思路AC代码CPython问题 C: 1.4 爱因斯坦的阶梯题目描述输入输出解题思路…...
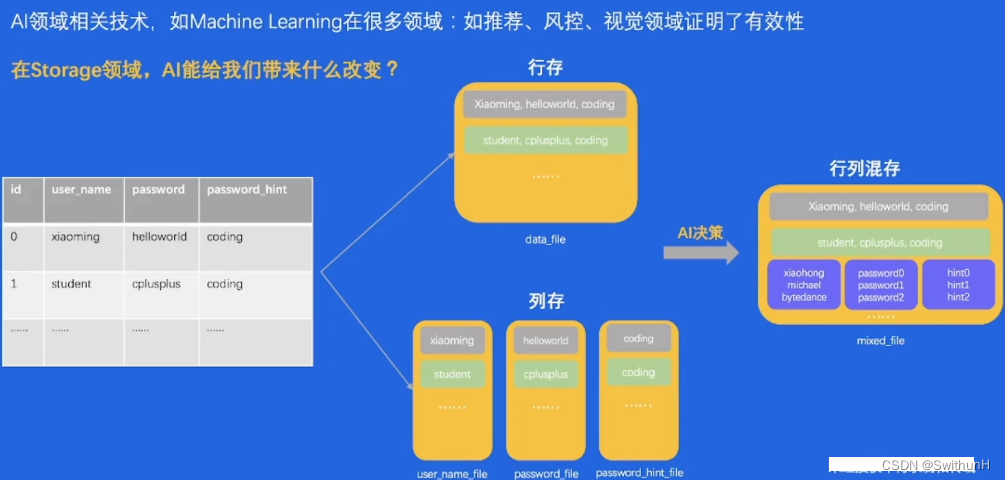
存储的本质-学习笔记
1 经典案例 1.1 数据的流动 一条用户注册数据流动到后端服务器,持久化保存到数据库中。 1.2 数据的持久化 校验数据的合法性修改内存写入存储介质2 存储&数据库简介 2.1 存储系统特点 性能敏感、容易受硬件影响、存储系统代码既“简单”又“复杂”。 2.2 数…...

新一代骨传导机皇重磅发布:南卡Neo骨传导运动耳机,性能全面提升
近日,中国最强骨传导品牌NANK南卡发布了最新一代骨传导耳机——南卡Neo骨传导耳机!该款耳机与运动专业性更强的南卡runner Pro4略微不同,其主要定位于轻运动风格,所以这款耳机的音质和佩戴舒适度达到了令人咂舌的地步!…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
