代码随想录算法训练DAY22|二叉树8
算法训练DAY22|二叉树8
235. 二叉搜索树的最近公共祖先
力扣题目链接(opens new window)
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
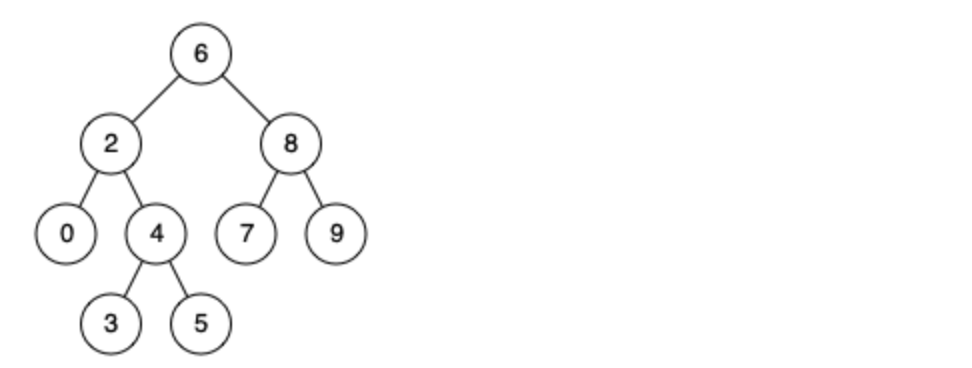
示例 1:
-
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
-
输出: 6
-
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
-
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
-
输出: 2
-
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
-
所有节点的值都是唯一的。
-
p、q 为不同节点且均存在于给定的二叉搜索树中。
思路
做过二叉树:公共祖先问题 (opens new window)题目的同学应该知道,利用回溯从底向上搜索,遇到一个节点的左子树里有p,右子树里有q,那么当前节点就是最近公共祖先。
那么本题是二叉搜索树,二叉搜索树是有序的,那得好好利用一下这个特点。
在有序树里,如果判断一个节点的左子树里有p,右子树里有q呢?
因为是有序树,所有 如果 中间节点是 q 和 p 的公共祖先,那么 中节点的数组 一定是在 [p, q]区间的。即 中节点 > p && 中节点 < q 或者 中节点 > q && 中节点 < p。
那么只要从上到下去遍历,遇到 cur节点是数值在[p, q]区间中则一定可以说明该节点cur就是p 和 q的公共祖先。 那问题来了,一定是最近公共祖先吗?
如图,我们从根节点搜索,第一次遇到 cur节点是数值在[q, p]区间中,即 节点5,此时可以说明 q 和 p 一定分别存在于 节点 5的左子树,和右子树中。
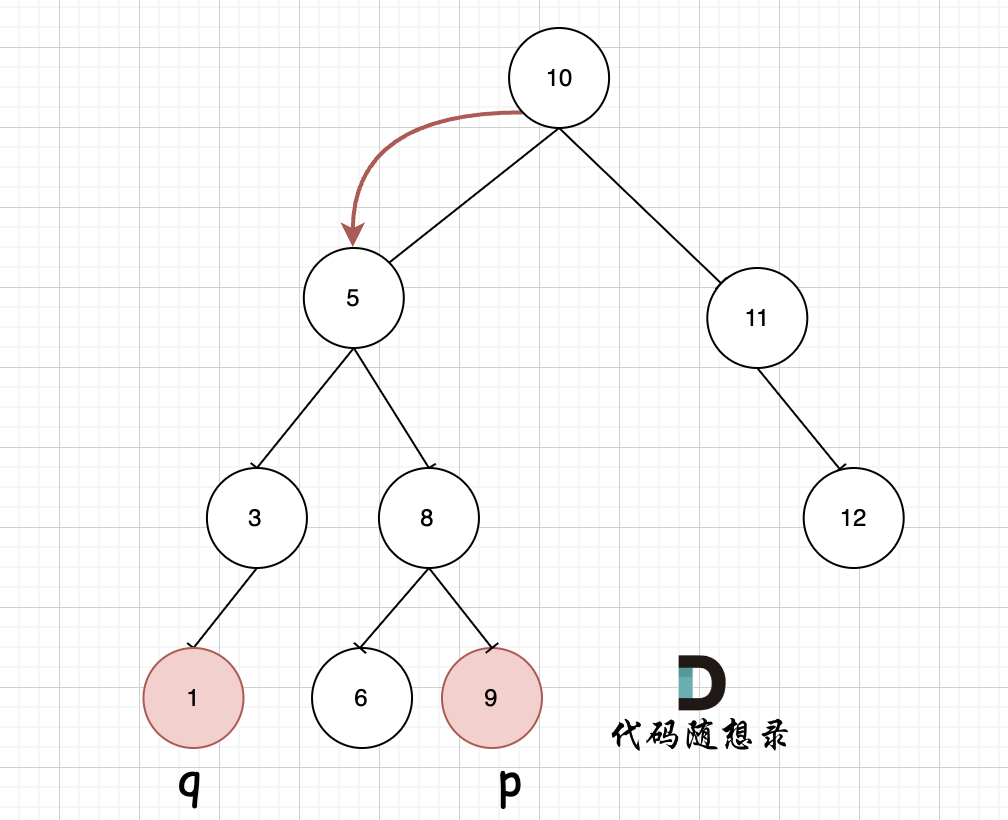
此时节点5是不是最近公共祖先? 如果 从节点5继续向左遍历,那么将错过成为p的祖先, 如果从节点5继续向右遍历则错过成为q的祖先。
所以当我们从上向下去递归遍历,第一次遇到 cur节点是数值在[q, p]区间中,那么cur就是 q和p的最近公共祖先。
理解这一点,本题就很好解了。
而递归遍历顺序,本题就不涉及到 前中后序了(这里没有中节点的处理逻辑,遍历顺序无所谓了)。
如图所示:p为节点6,q为节点9
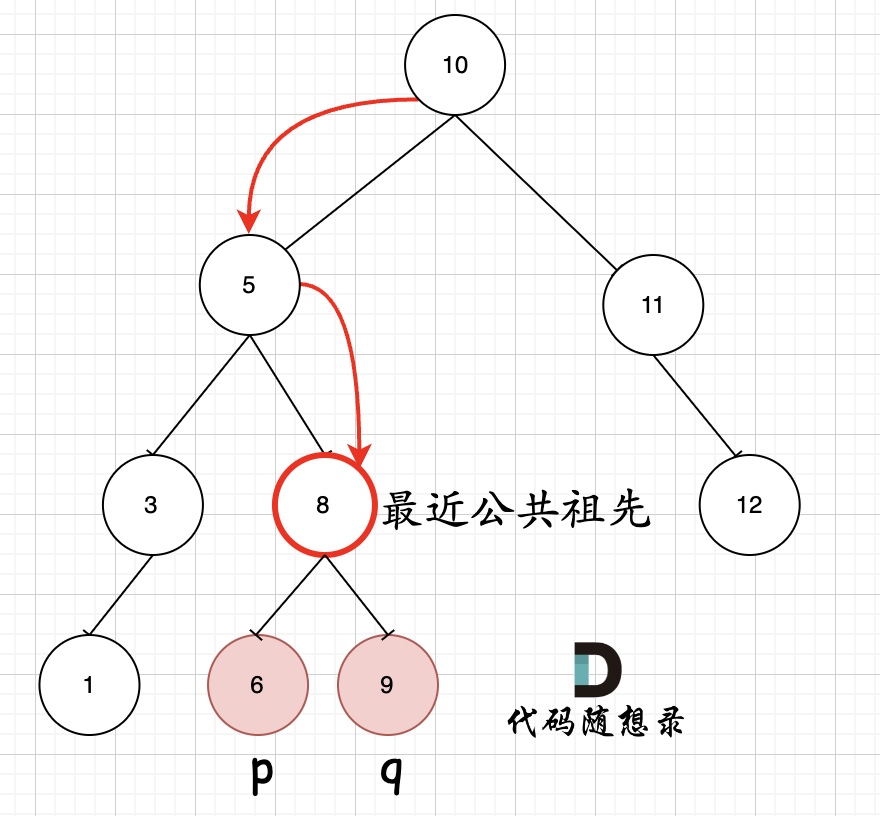
可以看出直接按照指定的方向,就可以找到节点8,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
#递归法
递归三部曲如下:
-
确定递归函数返回值以及参数
参数就是当前节点,以及两个结点 p、q。
返回值是要返回最近公共祖先,所以是TreeNode * 。
代码如下:
TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q)
-
确定终止条件
遇到空返回就可以了,代码如下:
if (cur == NULL) return cur;
其实都不需要这个终止条件,因为题目中说了p、q 为不同节点且均存在于给定的二叉搜索树中。也就是说一定会找到公共祖先的,所以并不存在遇到空的情况。
-
确定单层递归的逻辑
在遍历二叉搜索树的时候就是寻找区间[p->val, q->val](注意这里是左闭又闭)
那么如果 cur->val 大于 p->val,同时 cur->val 大于q->val,那么就应该向左遍历(说明目标区间在左子树上)。
需要注意的是此时不知道p和q谁大,所以两个都要判断
代码如下:
if (cur->val > p->val && cur->val > q->val) {TreeNode* left = traversal(cur->left, p, q);if (left != NULL) {return left;}
}
细心的同学会发现,在这里调用递归函数的地方,把递归函数的返回值left,直接return。
在二叉树:公共祖先问题 (opens new window)中,如果递归函数有返回值,如何区分要搜索一条边,还是搜索整个树。
搜索一条边的写法:
if (递归函数(root->left)) return ; if (递归函数(root->right)) return ;
搜索整个树写法:
left = 递归函数(root->left); right = 递归函数(root->right); left与right的逻辑处理;
本题就是标准的搜索一条边的写法,遇到递归函数的返回值,如果不为空,立刻返回。
如果 cur->val 小于 p->val,同时 cur->val 小于 q->val,那么就应该向右遍历(目标区间在右子树)。
if (cur->val < p->val && cur->val < q->val) {TreeNode* right = traversal(cur->right, p, q);if (right != NULL) {return right;}
}
剩下的情况,就是cur节点在区间(p->val <= cur->val && cur->val <= q->val)或者 (q->val <= cur->val && cur->val <= p->val)中,那么cur就是最近公共祖先了,直接返回cur。
代码如下:
return cur;
那么整体递归代码如下:
class Solution {
private:TreeNode* traversal(TreeNode* cur, TreeNode* p, TreeNode* q) {if (cur == NULL) return cur;// 中if (cur->val > p->val && cur->val > q->val) { // 左TreeNode* left = traversal(cur->left, p, q);if (left != NULL) {return left;}}
if (cur->val < p->val && cur->val < q->val) { // 右TreeNode* right = traversal(cur->right, p, q);if (right != NULL) {return right;}}return cur;}
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return traversal(root, p, q);}
};
精简后代码如下:
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root->val > p->val && root->val > q->val) {return lowestCommonAncestor(root->left, p, q);} else if (root->val < p->val && root->val < q->val) {return lowestCommonAncestor(root->right, p, q);} else return root;}
};
#迭代法
对于二叉搜索树的迭代法,大家应该在二叉树:二叉搜索树登场! (opens new window)就了解了。
利用其有序性,迭代的方式还是比较简单的,解题思路在递归中已经分析了。
迭代代码如下:
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {while(root) {if (root->val > p->val && root->val > q->val) {root = root->left;} else if (root->val < p->val && root->val < q->val) {root = root->right;} else return root;}return NULL;}
};
灵魂拷问:是不是又被简单的迭代法感动到痛哭流涕?
#总结
对于二叉搜索树的最近祖先问题,其实要比普通二叉树公共简单的多。
不用使用回溯,二叉搜索树自带方向性,可以方便的从上向下查找目标区间,遇到目标区间内的节点,直接返回。
最后给出了对应的迭代法,二叉搜索树的迭代法甚至比递归更容易理解,也是因为其有序性(自带方向性),按照目标区间找就行了。
701.二叉搜索树中的插入操作
力扣题目链接
给定二叉搜索树(BST)的根节点和要插入树中的值,将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据保证,新值和原始二叉搜索树中的任意节点值都不同。
注意,可能存在多种有效的插入方式,只要树在插入后仍保持为二叉搜索树即可。 你可以返回任意有效的结果。

提示:
-
给定的树上的节点数介于 0 和 10^4 之间
-
每个节点都有一个唯一整数值,取值范围从 0 到 10^8
-
-10^8 <= val <= 10^8
-
新值和原始二叉搜索树中的任意节点值都不同
思路
这道题目其实是一道简单题目,但是题目中的提示:有多种有效的插入方式,还可以重构二叉搜索树,一下子吓退了不少人,瞬间感觉题目复杂了很多。
其实可以不考虑题目中提示所说的改变树的结构的插入方式。
如下演示视频中可以看出:只要按照二叉搜索树的规则去遍历,遇到空节点就插入节点就可以了。
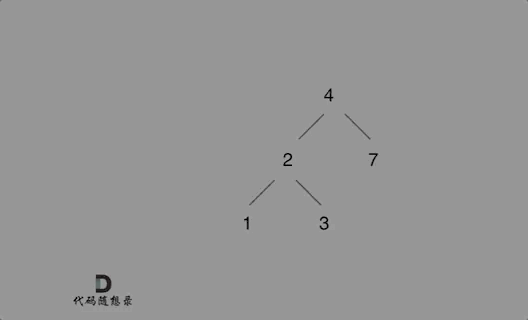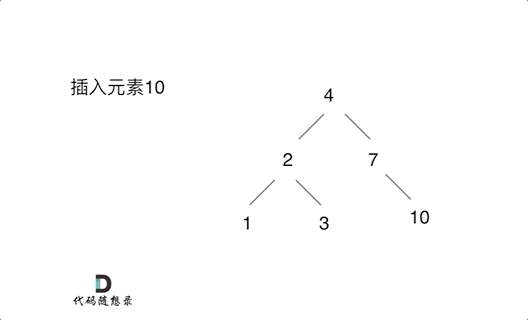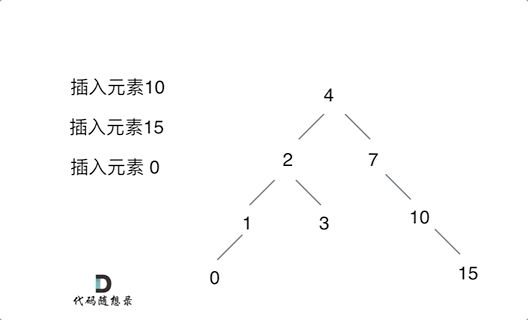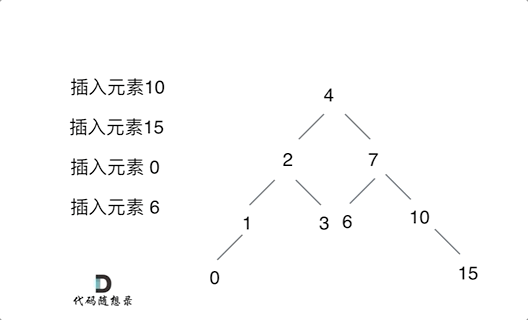
例如插入元素10 ,需要找到末尾节点插入便可,一样的道理来插入元素15,插入元素0,插入元素6,需要调整二叉树的结构么? 并不需要。。
只要遍历二叉搜索树,找到空节点 插入元素就可以了,那么这道题其实就简单了。
接下来就是遍历二叉搜索树的过程了。
#递归
递归三部曲:
-
确定递归函数参数以及返回值
参数就是根节点指针,以及要插入元素,这里递归函数要不要有返回值呢?
可以有,也可以没有,但递归函数如果没有返回值的话,实现是比较麻烦的,下面也会给出其具体实现代码。
有返回值的话,可以利用返回值完成新加入的节点与其父节点的赋值操作。(下面会进一步解释)
递归函数的返回类型为节点类型TreeNode * 。
代码如下:
TreeNode* insertIntoBST(TreeNode* root, int val)
-
确定终止条件
终止条件就是找到遍历的节点为null的时候,就是要插入节点的位置了,并把插入的节点返回。
代码如下:
if (root == NULL) {TreeNode* node = new TreeNode(val);return node;
}
这里把添加的节点返回给上一层,就完成了父子节点的赋值操作了,详细再往下看。
-
确定单层递归的逻辑
此时要明确,需要遍历整棵树么?
别忘了这是搜索树,遍历整棵搜索树简直是对搜索树的侮辱。
搜索树是有方向了,可以根据插入元素的数值,决定递归方向。
代码如下:
if (root->val > val) root->left = insertIntoBST(root->left, val); if (root->val < val) root->right = insertIntoBST(root->right, val); return root;
到这里,大家应该能感受到,如何通过递归函数返回值完成了新加入节点的父子关系赋值操作了,下一层将加入节点返回,本层用root->left或者root->right将其接住。
整体代码如下:
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) {TreeNode* node = new TreeNode(val);return node;}if (root->val > val) root->left = insertIntoBST(root->left, val);if (root->val < val) root->right = insertIntoBST(root->right, val);return root;}
};
可以看出代码并不复杂。
刚刚说了递归函数不用返回值也可以,找到插入的节点位置,直接让其父节点指向插入节点,结束递归,也是可以的。
那么递归函数定义如下:
TreeNode* parent; // 记录遍历节点的父节点 void traversal(TreeNode* cur, int val)
没有返回值,需要记录上一个节点(parent),遇到空节点了,就让parent左孩子或者右孩子指向新插入的节点。然后结束递归。
代码如下:
class Solution {
private:TreeNode* parent;void traversal(TreeNode* cur, int val) {if (cur == NULL) {TreeNode* node = new TreeNode(val);if (val > parent->val) parent->right = node;else parent->left = node;return;}parent = cur;if (cur->val > val) traversal(cur->left, val);if (cur->val < val) traversal(cur->right, val);return;}
public:TreeNode* insertIntoBST(TreeNode* root, int val) {parent = new TreeNode(0);if (root == NULL) {root = new TreeNode(val);}traversal(root, val);return root;}
};
可以看出还是麻烦一些的。
我之所以举这个例子,是想说明通过递归函数的返回值完成父子节点的赋值是可以带来便利的。
网上千篇一律的代码,可能会误导大家认为通过递归函数返回节点 这样的写法是天经地义,其实这里是有优化的!
#迭代
跳过
450.删除二叉搜索树中的节点
力扣题目链接
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
首先找到需要删除的节点; 如果找到了,删除它。 说明: 要求算法时间复杂度为 $O(h)$,h 为树的高度。
示例:

思路
搜索树的节点删除要比节点增加复杂的多,有很多情况需要考虑,做好心理准备。
#递归
递归三部曲:
-
确定递归函数参数以及返回值
说到递归函数的返回值,在二叉树:搜索树中的插入操作 (opens new window)中通过递归返回值来加入新节点, 这里也可以通过递归返回值删除节点。
代码如下:
TreeNode* deleteNode(TreeNode* root, int key)
1
-
确定终止条件
遇到空返回,其实这也说明没找到删除的节点,遍历到空节点直接返回了
if (root == nullptr) return root;
1
-
确定单层递归的逻辑
这里就把二叉搜索树中删除节点遇到的情况都搞清楚。
有以下五种情况:
-
第一种情况:没找到删除的节点,遍历到空节点直接返回了
-
找到删除的节点
-
第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
-
第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
-
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
-
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
-
第五种情况有点难以理解,看下面动画:

动画中的二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
将删除节点(元素7)的左孩子放到删除节点(元素7)的右子树的最左面节点(元素8)的左孩子上,就是把5为根节点的子树移到了8的左孩子的位置。
要删除的节点(元素7)的右孩子(元素9)为新的根节点。.
这样就完成删除元素7的逻辑,最好动手画一个图,尝试删除一个节点试试。
代码如下:
if (root->val == key) {// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点if (root->left == nullptr) return root->right;// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点else if (root->right == nullptr) return root->left;// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置TreeNode* tmp = root; // 把root节点保存一下,下面来删除root = root->right; // 返回旧root的右孩子作为新rootdelete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)return root;}
}
这里相当于把新的节点返回给上一层,上一层就要用 root->left 或者 root->right接住,代码如下:
if (root->val > key) root->left = deleteNode(root->left, key); if (root->val < key) root->right = deleteNode(root->right, key); return root;
整体代码如下:(注释中:情况1,2,3,4,5和上面分析严格对应)
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了if (root->val == key) {// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置TreeNode* tmp = root; // 把root节点保存一下,下面来删除root = root->right; // 返回旧root的右孩子作为新rootdelete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};
普通二叉树的删除方式
这里我在介绍一种通用的删除,普通二叉树的删除方式(没有使用搜索树的特性,遍历整棵树),用交换值的操作来删除目标节点。
代码中目标节点(要删除的节点)被操作了两次:
-
第一次是和目标节点的右子树最左面节点交换。
-
第二次直接被NULL覆盖了。
思路有点绕,感兴趣的同学可以画图自己理解一下。
代码如下:(关键部分已经注释)
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root;if (root->val == key) {if (root->right == nullptr) { // 这里第二次操作目标值:最终删除的作用return root->left;}TreeNode *cur = root->right;while (cur->left) {cur = cur->left;}swap(root->val, cur->val); // 这里第一次操作目标值:交换目标值其右子树最左面节点。}root->left = deleteNode(root->left, key);root->right = deleteNode(root->right, key);return root;}
};
这个代码是简短一些,思路也巧妙,但是不太好想,实操性不强,推荐第一种写法!
相关文章:

代码随想录算法训练DAY22|二叉树8
算法训练DAY22|二叉树8 235. 二叉搜索树的最近公共祖先 力扣题目链接(opens new window) 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点…...

如何解决跨域问题
跨域是什么 跨域是指在浏览器中运行的前端程序试图通过XMLHttpRequest等方式向不同域的后端服务器发送请求时,会遭遇浏览器同源策略限制的情况默认情况下,浏览器只允许在同一来源(协议、域名、端口)下进行请求,而跨域…...
Typora 编辑器 讲解 包括使用方式 快捷键 附带下载地址 (免费破解)
CSDN 成就一亿技术人! 今天来讲一下很好用的编辑器 Typora CSDN 成就一亿技术人! 什么是Typora? 它是一个 Markdown 编辑器和阅读器,这意味着您可以使用简单的格式代码 (Markdown)是一种轻量级标记语言&…...

16-Echarts简化系列之:平行坐标系 parallel 和 parallelAxis 坐标轴
parallel: 可视化高维数据的图表,特点在于可同时展示多个变量之间的关系,并且可以通过调整轴的顺序和缩放来探索不同的数据视角。帮助探索数据之间的关系和趋势 parallelAxis: 平行坐标系中的坐标轴。 parallel 和 parallelAx…...

SqlServer内存使用情况
-- 查询执行中sql语句 SELECT TOP 500 [session_id], [request_id], [start_time] AS 开始时间, getdate() as 当前时间, [status] AS 状态, [command] AS 命令, dest.[text] AS sql语句, DB_NAME([database_id]) AS 数据库名, [blocking_session_id] AS 正在阻塞其他会话的会话…...

谈谈我的三次考研经历
阿七经历过三次考研。 第一次,大四毕业那年,大三开始有紧迫感,因为大学几年什么也没学会,毕业考试成绩从第二个学期开始就一路下滑,每次都是考前一周突击,最后擦着及格线通过。 大三就开始和几个同学组队…...

红队打靶练习:SAR: 1
目录 信息收集 1、arp 2、netdiscover 3、nmap 4、nikto 5、whatweb 小结 目录探测 1、gobuster 2、dirsearch WEB CMS 1、cms漏洞探索 2、RCE漏洞利用 提权 get user.txt 本地提权 信息收集 1、arp ┌──(root㉿ru)-[~/kali] └─# arp-scan -l Interface:…...

WSL 与真实 linux 环境区别有多大?
随着 Windows 系统的不断发展和完善,WSL(Windows Subsystem for Linux)作为 Windows 10 的一个功能,为 Windows 用户提供了一个可以在 Windows 环境下运行 Linux 二进制可执行文件的环境。然而,尽管 WSL 为用户提供了一…...

Springboot和Spring有什么区别
SpringBoot和Spring的关系 不是:从马车到汽车那种交通出行的颠覆,从燃油车到纯电动车那种能源利用的变革,从人工驾驶到AI智能那种驾驶方式的升级。总之,不是产品的升级换代,不是谁要替换谁。而是:汽车从手…...
创建Qt项目
项目工程名称一般不要有特殊符号,不要有中文 项目工程保存路径可修改的,但路径不要带中文 构建系统,有3种,这里使用qmake qmake和cmake区别 构建过程不同,项目管理不同。 1、构建过程,qmake是Qt框架自带的…...
总目录)
钢铁企业电力设计手册(上下册)总目录
《钢铁企业电力设计手册》总目录 上册 第1章 高压供配电系统 第2章 负荷计算 第3章 供电系统中的有功和无功冲击负荷 第4章 短路电流计算 第5章 电压偏差和电压波动 第6章 电技术节能 第7章 自备电厂及柴油机组发电 第8章 电弧炉供电 第9章 能源管理系统(电力部分&a…...

Activemq存储KahaDb详解
引言 ActiveMQ在不提供持久化的情况下,数据保存在内存中,一旦应用崩溃或者重启之后,数据都将会丢失,这显然在大部分情况下是我们所不希望的。对此ActiveMQ提供了两种持久化方式以供选择。 kahaDB kahaDB是一个基于文件…...
)
嵌入式C语言--ROMRAM相关概念(RO-data、RW-data、ZI-data的解释)
嵌入式C语言–ROMRAM相关概念(RO-data、RW-data、ZI-data的解释) ROMRAM相关概念(RO-data、RW-data、ZI-data的解释) 嵌入式C语言--ROMRAM相关概念(RO-data、RW-data、ZI-data的解释)一. ROM(Re…...
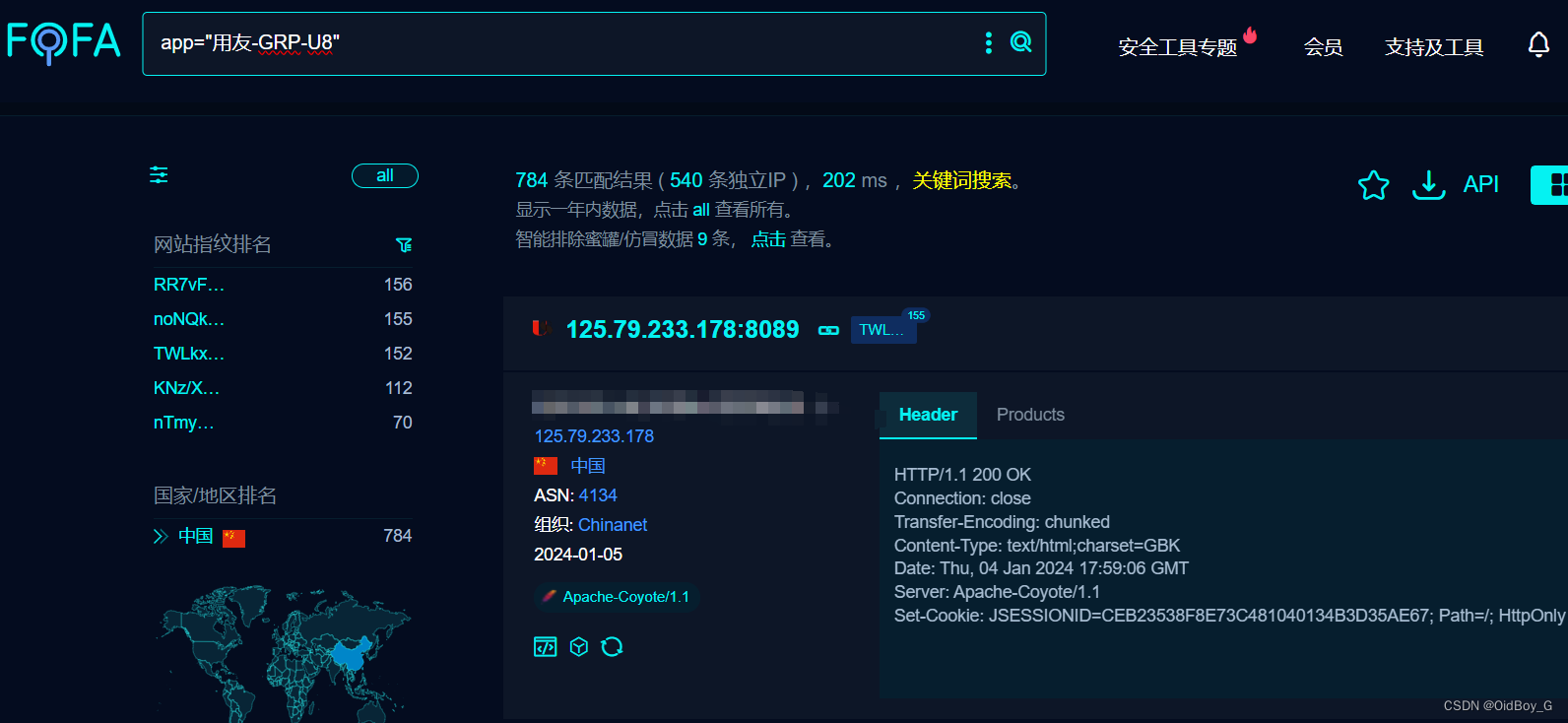
用友GRP-U8 ufgovbank.class XXE漏洞复现
0x01 产品简介 用友GRP-U8R10行政事业财务管理软件是用友公司专注于国家电子政务事业,基于云计算技术所推出的新一代产品,是我国行政事业财务领域最专业的政府财务管理软件。 0x02 漏洞概述 用友GRP-U8R10 ufgovbank.class 存在XML实体注入漏洞,攻击者可利用xxe漏洞获取服…...
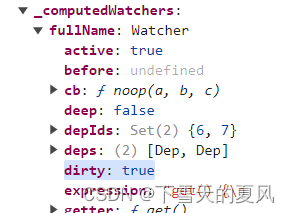
Vue2 - computed 和 method 的原理区别
目录 1,简单对比2,原理的不同1,method 的处理2,computed 的处理实现缓存触发更新 3,触发更新时的问题 1,简单对比 computed 当做属性使用,method 当做方法使用。computed 可以提供 getter 和 s…...

Python开发环境搭建
Python程序设计语言是解释型语言,其广泛应用于运维开发领域、数据分析领域、人工智能领域,本文主要描述Python开发环境的搭建。 www.python.org 如上所示,从官方网站下载Python最新的稳定版本3.12.1 如上所示,在本地的开发环境安…...

使用Go语言的HTTP客户端进行并发请求
Go语言是一种高性能、简洁的编程语言,它非常适合用于构建并发密集型的网络应用。在Go中,标准库提供了强大的HTTP客户端和服务器功能,使得并发HTTP请求变得简单而高效。 首先,让我们了解为什么需要并发HTTP请求。在许多应用场景中…...

吴恩达深度学习l2week2编程作业—Optimization Methods(最新中文跑通版)
到目前为止,您一直使用渐变下降来更新参数并将成本降至最低。在本笔记本中,您将获得一些更先进的优化方法的技能,这些方法可以加快学习速度,甚至可能使您获得更好的成本函数最终值。拥有一个好的优化算法可能是等待几天与只需几个…...

每日一题——LeetCode1089.复写0
方法一 splice: 通过数组的slice方法,碰到 0就在后面加一个0,最后截取原数组的长度,舍弃后面部分。 但这样做是违反了题目的要求,不要在超过该数组长度的位置写入元素。 var duplicateZeros function(arr) {var le…...
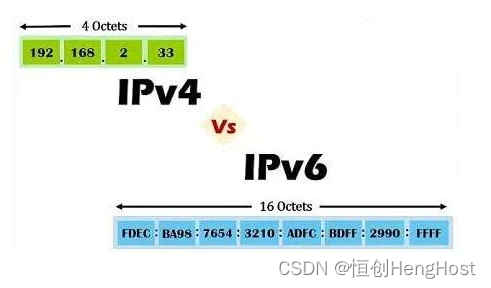
IPv6和IPv4在技术层面的区别
随着互联网的不断发展,IPv4地址资源已经逐渐枯竭,而IPv6地址的使用逐渐成为趋势。IPv6和IPv4作为互联网协议的两个版本,在技术层面存在许多区别。本文将从地址空间、地址表示方法、路由协议、安全性、移动性以及网络性能等方面对IPv6和IPv4进…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...
