优化|流形优化系列(一)

简介
流形优化是非线性优化的一个分支,它主要关注在特定的几何结构下进行优化。在流形优化中,优化问题通常是在黎曼流形上进行的,而非欧几里得空间。黎曼流形是带有黎曼度量的流形,该度量为流形上的每个点都定义了一个内积。这种内积结构提供了流形上测量长度和角度的方式,这在优化过程中非常重要,因为它允许我们定义梯度和Hessian等概念,并进行相应的优化操作。在流形优化的背景下,流形通常是解的约束集。例如,当解必须是正交矩阵、单位范数向量或其它特殊结构时,这些集合都可以被看作流形。对于连续优化,讨论多面体是考虑线性优化问题的基础,而在欧几里得空间中的微积分被用于发展非线性欧几里得优化理论。同样地,黎曼流形上的微积分,借助微分几何学(尤其是黎曼几何学)得以促进,对于黎曼流形上的优化是至关重要的。
流形优化相对于传统欧几里得空间上的优化方法,优势在于:
- 在黎曼流形上迭代,减少建模误差,提高一些非线性问题的表示能力;
- 充分利用目标函数的内在几何结构,通过选取合适的黎曼度量可将一些非凸优化问题转化为凸优化问题;
- 保持最优化问题的尺度不变性。
在各个应用领域的需求牵引下,相关学者的研究工作极大地促进了黎曼流形优化理论的发展与工程应用,如Hermitian 特征值问题、自适应正则化、迹范数、相机位姿估计、经济负载分配、对称特征值问题、低秩矩阵填充等,其技术成果已成功应用于相关学科,如航空航天、理论物理、无线通信、医学成像、自动控制、计算机视觉等。
推荐感兴趣的同学阅读参考文献中的书目。
流形优化基础知识
从黎曼流形的概念开始,用 M \mathcal{M} M表示一个有限维的黎曼流形,并用 T p M T_p\mathcal{M} TpM 表示 M \mathcal{M} M 在点 p p p处的切平面。在 M \mathcal{M} M的每一点 p p p上,都有一个内积 ⟨ ⋅ , ⋅ ⟩ p \langle \cdot, \cdot \rangle_p ⟨⋅,⋅⟩p定义在切空间 T p M T_p\mathcal{M} TpM上。黎曼度量 ⟨ ⋅ , ⋅ ⟩ p \langle \cdot , \cdot \rangle_p ⟨⋅,⋅⟩p 相关的范数记作 ∥ ⋅ ∥ p \|\cdot\| _p ∥⋅∥p。用 $l(\gamma) $来表示分段光滑曲线 γ : [ a , b ] → M \gamma : [a, b] \rightarrow \mathcal{M} γ:[a,b]→M的长度。
流形优化的基本问题形式为:
min x ∈ M f ( x ) \min_{x \in \mathcal{M}} f(x) x∈Mminf(x)
其中$f: \mathcal{M} \to \mathbb{R} , , ,\mathcal{M}$是一个黎曼流形。
常见流形
以下是一些在流形优化中常用的流形例子:
-
球面流形 (Sphere Manifold):
考虑单位球面 S n − 1 S^{n-1} Sn−1 在 R n \mathbb{R}^n Rn 中,定义为:
S n − 1 = { x ∈ R n : ∥ x ∥ 2 = 1 } S^{n-1} = \{ x \in \mathbb{R}^n : \|x\|_2 = 1 \} Sn−1={x∈Rn:∥x∥2=1}
此流形上的点是具有单位范数的 R n \mathbb{R}^n Rn 中的向量。这是一个常见的约束,特别是在需要正则化或单位范数约束的优化问题中。 -
正交流形 (Stiefel Manifold):
考虑所有有 n n n行和 p p p 列的列正交矩阵的集合。它可以表示为:
S t ( n , p ) = { X ∈ R n × p : X T X = I p } St(n, p) = \{ X \in \mathbb{R}^{n \times p} : X^T X = I_p \} St(n,p)={X∈Rn×p:XTX=Ip}
其中 I p I_p Ip 是 p × p p \times p p×p的单位矩阵。这种流形在子空间迭代和降维技术中很有用。 -
正定锥流形 (Positive Definite Manifold):
考虑所有 n × n n \times n n×n正定矩阵的集合。这是一个在半正定编程和统计中非常重要的约束集。
-
Grassmann 流形:
定义为 n n n 维空间中所有 p p p 维线性子空间的集合。与 Stiefel 流形相比,Grassmann 流形不考虑子空间的基的选取,只考虑子空间本身。
基础概念
当我们考虑流形优化问题时,特别是在黎曼流形上,优化的算法需要考虑流形的几何结构。为此,我们引入一些特定的概念,如黎曼梯度、收缩映射(retraction)和向量传输(vector transport)。以下是这些概念的定义:
-
黎曼梯度 (Riemannian Gradient):
对于定义在流形 M \mathcal{M} M上的实值函数 f f f,其在点 p p p处的黎曼梯度,记作 grad p f \text{grad}_p f gradpf,是流形 M \mathcal{M} M上的一个切向量,与欧氏梯度 ∇ f ( p ) \nabla f(p) ∇f(p)在该点的内积最大。数学上,它满足以下关系:
⟨ grad p f , v ⟩ p = D v f ( p ) , ∀ v ∈ T p M \langle \text{grad}_p f, v \rangle_p = D_v f(p),\quad \forall v\in{T_p}\mathcal{M} ⟨gradpf,v⟩p=Dvf(p),∀v∈TpM
其中 D v f ( p ) D_vf(p) Dvf(p)是函数 f f f在点 p p p处沿着方向 v v v的方向导数,而 ⟨ ⋅ , ⋅ ⟩ p \langle \cdot, \cdot \rangle_p ⟨⋅,⋅⟩p 是点 p p p处的黎曼度量。
-
收缩 (Retraction):
让我们从流形上的一点 p p p开始,并考虑一个从该点出发的切向量 v v v。收缩映射 R p ( v ) R_p(v) Rp(v) 提供了一个近似的方法来移动到流形上另一点,从而在某种意义上对黎曼指数映射进行了近似。
严格地说,对于给定的点 p p p和切向量 v v v,收缩映射 R p : T p M → M R_p: T_p\mathcal{M} \to \mathcal{M} Rp:TpM→M 满足以下两个条件:- R p ( 0 ) = p R_p(0) = p Rp(0)=p
- R p R_p Rp 在 0 0 0处是连续的

- 传输 (Transport):
传输定义了如何将流形上一点的切空间中的向量“移动”到另一点的切空间中,而不改变其“方向”。设 T p M T_p\mathcal{M} TpM和 T q M T_q\mathcal{M} TqM 分别是流形 M \mathcal{M} M 上点 p p p和 q q q的切空间,传输是一个映射:
T p ( v ) : T p M → T q M T_p(v) : T_p\mathcal{M} \to T_q\mathcal{M} Tp(v):TpM→TqM
其中流形优化中两种常用的传输方式是:平行传输(parallel transport)和向量传输(vector transport)。
常见算法
有了上面提及的这些概念,类似欧式空间中的梯度下降法更新公式 x k + 1 = x k + t k d k x^{k+1} = x^k + t^kd^k xk+1=xk+tkdk,我们可以简单的得到流形上的梯度下降算法的更新公式
x k + 1 = R x k ( − t k grad x k f ) x^{k+1} = R_x^{k}(-t^k \text{grad}_{x^{k}} f) xk+1=Rxk(−tkgradxkf)
其中 t k t^k tk是步长, R x k R_x^{k} Rxk是在点 x k x^{k} xk的收缩映射。
流形上的梯度下降法的关键在于如何正确地“移动”在流形上。由于流形的几何约束,我们不能简单地进行线性更新,而是需要利用流形的几何结构进行更新。黎曼梯度和收缩映射是这个过程中的核心组成部分。
近年来多种传统优化算法已成功地被扩展到流形优化领域,包括梯度下降,共轭梯度法,随机梯度下降法,牛顿法,信赖域法,内点法,BFGS和ADMM等。需要注意的区别是,流形上的梯度及Hessian矩阵信息也与流形本身有关(黎曼梯度和黎曼Hessian矩阵),同时更新过程也将依赖于收缩映射和传输,这些操作确保算法在流形的几何约束内进行迭代,并保持算法的稳定性和收敛性。因此,对流形及其相关知识的深入了解和熟悉变得尤为重要。
流形优化计算工具
Manopt
Manopt 是一个专门为研究人员和工程师设计的优化工具箱,旨在简化和推动定义在流形上的优化问题的解决过程。Manopt 提供了一系列工具和算法,帮助用户轻松地在各种流形结构上设置和解决优化问题。Manopt 的优势在于它的灵活性和易用性。它支持多种流形结构,如正定对称矩阵、Stiefel流形和球面流形等。此外,它的设计目标是为用户提供一个简单、直观的接口,使用户无需深入了解流形优化的复杂性就可以轻松应用。此外,Manopt 还拥有丰富的文档和教程,帮助新手快速上手,同时为经验丰富的研究者提供高级功能和自定义选项。
PyManopt是Manopt的Python版本,Manopt.jl是为Julia编程语言设计的Manopt版本。
实例
我们考虑Manopt官方给出的实例。计算对称矩阵 A ∈ R n × n A \in \mathbb{R}^{n\times n} A∈Rn×n 的主要特征向量。设 λ 1 ≥ ⋯ ≥ λ n \lambda_1 \geq \cdots \geq \lambda_n λ1≥⋯≥λn 是其特征值。最大的特征值, λ 1 \lambda_1 λ1,是以下优化问题的最优值:
max x ∈ R n , x ≠ 0 x ⊤ A x x ⊤ x . \max\limits_{x\in\mathbb{R}^n, x \neq 0} \frac{x^\top A x}{x^\top x}. x∈Rn,x=0maxx⊤xx⊤Ax.
问题可以改写为:
min x ∈ R n , ∥ x ∥ = 1 − x ⊤ A x . \min\limits_{x\in\mathbb{R}^n, \|x\| = 1} -x^\top A x. x∈Rn,∥x∥=1min−x⊤Ax.
函数及其在 R n \mathbb{R}^n Rn 中的梯度为:
f ( x ) = − x ⊤ A x , ∇ f ( x ) = − 2 A x . \begin{align} f(x) & = -x^\top A x, \nonumber\\ \nabla f(x) & = -2Ax. \nonumber \end{align} f(x)∇f(x)=−x⊤Ax,=−2Ax.
向量 x x x 的约束要求 x x x 具有单位2-范数,即 x x x 是球面上的一点:
S n − 1 = { x ∈ R n : x ⊤ x = 1 } . \mathbb{S}^{n-1} = \{x \in \mathbb{R}^n : x^\top x = 1\}. Sn−1={x∈Rn:x⊤x=1}.
这是我们应用 Manopt 解决问题所需要的所有信息。
函数 f f f在 S n − 1 \mathbb{S}^{n-1} Sn−1 上是光滑的。它在 S n − 1 \mathbb{S}^{n-1} Sn−1上 x x x 处的黎曼梯度 是 x x x 处球的切线向量。它可以计算为从常规梯度 ∇ f ( x ) \nabla f(x) ∇f(x) 到该切线空间的投影,使用正交投影器 P r o j x u = ( I − x x ⊤ ) u \mathrm{Proj}_x u = (I-xx^\top)u Projxu=(I−xx⊤)u:
g r a d f ( x ) = P r o j x ∇ f ( x ) = − 2 ( I − x x ⊤ ) A x . \mathrm{grad}\,f(x) = \mathrm{Proj}_x \nabla f(x) = -2(I-xx^\top)Ax. gradf(x)=Projx∇f(x)=−2(I−xx⊤)Ax.
这是欧几里得梯度 ∇ f \nabla f ∇f 与黎曼梯度 g r a d f \mathrm{grad}\,f gradf 之间的数学关系的一个示例,我们通常已经知道如何从微积分课程中计算 ∇ f \nabla f ∇f,并且为优化需要 g r a d f \mathrm{grad}\,f gradf。在 Manopt 中,转换是在后台通过一个名为 egrad2rgrad 的函数完成的,我们只需要计算 ∇ f \nabla f ∇f。
以下是使用Manopt 中的信赖域法解决这个优化问题的代码:
% 生成随机问题数据n = 1000;A = randn(n);A = .5*(A+A.');% 创建问题结构manifold = spherefactory(n);problem.M = manifold;% 定义问题成本函数及其欧几里得梯度。problem.cost = @(x) -x'*(A*x);problem.egrad = @(x) -2*A*x;% 注意 'e' 在 'egrad' 中代表欧几里得% 数值检查梯度一致性(可选)checkgradient(problem);% 解决[x, xcost, info, options] = trustregions(problem);% 显示一些统计数据figure;semilogy([info.iter], [info.gradnorm], '.-');xlabel('迭代次数');ylabel('f 的梯度的范数');
运行结果:

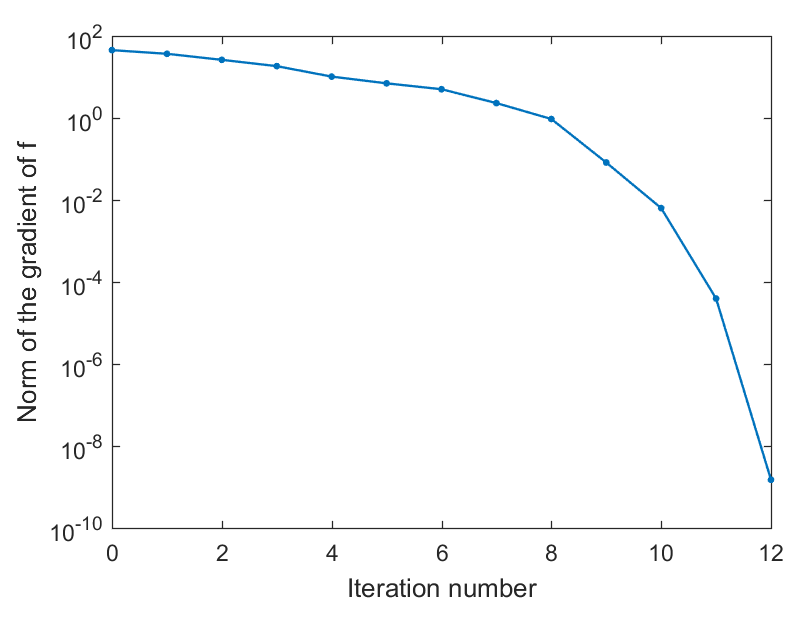
在之后的系列中,我们会对上述提到的流形优化中的常见基本概念和算法进行详细的分析。
参考文献
- Absil P A, Mahony R, Sepulchre R. Optimization algorithms on matrix manifolds[M]. Princeton University Press, 2008.
- Boumal N. An introduction to optimization on smooth manifolds[M]. Cambridge University Press, 2023.
- Sato H. Riemannian optimization and its applications[M]. Berlin: Springer, 2021.
- 潘汉,黎曼流形优化及其应用, 北京, 科学出版社, 2020
- 刘浩洋, 户将, 李勇锋,文再文,最优化:建模、算法与理论, 第二版草稿, 7.4 流形约束优化算法
相关文章:

优化|流形优化系列(一)
简介 流形优化是非线性优化的一个分支,它主要关注在特定的几何结构下进行优化。在流形优化中,优化问题通常是在黎曼流形上进行的,而非欧几里得空间。黎曼流形是带有黎曼度量的流形,该度量为流形上的每个点都定义了一个内积。这种…...
函数)
torch.where()函数
在深度学习的实现中,处理条件逻辑是一项常见而重要的任务。PyTorch 提供了一个强大的函数 torch.where(),它使得基于条件的张量操作变得既简单又高效。本文将深入探讨 torch.where() 的用法,并通过示例展示它在不同场景中的应用。 什么是 to…...

盖子的c++小课堂——第二十三讲:背包问题
前言 又是一次漫长的更新(我真不是故意的aaaaaaaaaaaaaaa),先不多说了,直接给我~坐下~说错了说错了,直接开始~ 背包问题----动态规划 背包问题(knapsack problem) 动态规划(dyna…...

k8s安装hostPath方式存储的PostgreSQL15
1.配置 PostgreSQL 的 ConfigMap cat > postgres-configmap.yaml << EOF apiVersion: v1 kind: ConfigMap metadata:name: postgres-configlabels:app: postgresnamespace: dev data:POSTGRES_DB: postgresdbPOSTGRES_USER: postgresadminPOSTGRES_PASSWORD: admin12…...
51单片机之按键和数码管
51单片机之按键和数码管 ✍前言:♐独立按键😀独立按键的原理😀软件实现按键控制LED灯的亮灭 ♐数码管😊数码管显示数字或者字母的原理🐉共阳极数码管🐉共阴极极数码管🐉4位1体数码管 Ƕ…...

【Oracle】 - 数据库的实例、表空间、用户、表之间关系
Oracle是一种广泛使用的关系型数据库管理系统,它具有高性能、高可靠性、高安全性等特点。1Oracle数据库的结构和组成是一个复杂而又有趣的话题,本文将介绍Oracle数据库的四个基本概念:数据库、实例、表空间和用户,以及它们之间的关…...
ssm基于HTML5的交流论坛的设计与实现+vue论文
摘 要 信息数据从传统到当代,是一直在变革当中,突如其来的互联网让传统的信息管理看到了革命性的曙光,因为传统信息管理从时效性,还是安全性,还是可操作性等各个方面来讲,遇到了互联网时代才发现能补上自古…...

JDBC*
*JDBC数据库连接步骤 1.将JDBC驱动的jar添加到项目的依赖中。 2.加载JDBC驱动 例如: Class.forName("com.mysql.jdbc.Driver"); 3.连接数据库 例如: Connection con DriverManager.getConnection(URL,us…...

Zookeeper注册中心实战
Java学习手册面试指南:https://javaxiaobear.cn Spring Cloud Zookeeper通过自动配置和绑定到 Spring 环境和其他 Spring 编程模型习惯用法,为 Spring Boot 应用程序提供Apache Zookeeper集成。通过一些简单的注释,您可以快速启用和配置应用…...
1-02VS的安装与测试
一、概述 对于一名C语言程序员而言,进行C语言程序的开发一般需要一个文本编辑器加上一个编译器就足够了。但为了方便起见,我们选择使用集成开发环境——Visual Studio(简称VS)。安装Visual Studio 下面讲一下如何安装VS࿰…...
ctfshow——PHP特性
文章目录 web 89web 90web 91web 92web 93web 94web 95web 96web 97web 98web 99web 100——优先级、eval()用法web 101——RefelctionClass反射类web 102——php伪协议、hex2bin()web103web 104——sha1绕过web 105 web 89 使用人工分配 ID 键的数值型数组绕过preg_match. 两个…...

K8S陈述式资源管理
陈述式 命令行:kubectl命令行工具 优点:90%以上的场景都可以满足,对增,删,查比较方便,对改不是很友好 缺点:命令比较冗长,复杂,难记 声明式 k8s当中的yaml文件来实现资…...

详解Python内置函数 !!!
内置函数就是Python给你提供的, 拿来直接用的函数,比如print,input等。 文章目录 前言 一、和数字相关 1. 数据类型 2. 进制转换 3. 数学运算 二、和数据结构相关 1. 序列 2. 数据集合 3. 相关内置函数 三、和数据结构相关 四、和迭代器生成器相关 五、字…...
)
使用Vue3 + Vite创建uni-app项目(Webstorm)
使用Vue3 Vite创建uni-app项目(Webstorm) 参考:前端VUE3Vite UniAPP-- 框架搭建_uniapp vite-CSDN博客 // 参考github.com的库:https://github.com/dcloudio/uni-preset-vue npx degit dcloudio/uni-preset-vue#vite-ts vite-vu…...
【js】js实现多个视频连续播放:
文章目录 一、效果:二、实现:三、案例: 一、效果: 二、实现: <!DOCTYPE html> <html> <head><title>Video Player</title><style>#progressBar { width: 800px;height: 20px;b…...
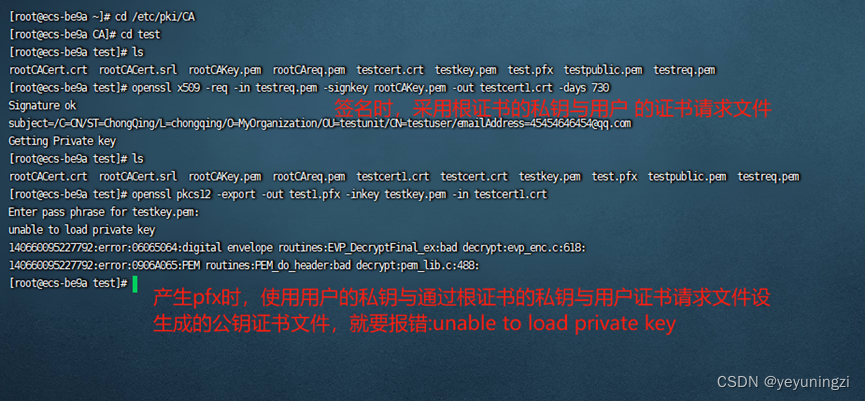
使用openssl 生成pfx格式证书时报错:unable to load certificates
问题现象包如下: 之前在centos上使用openssl部署证书服务器以及颁发证书的时候遇到的问题,在进行个人证书生成之后需要形成pfx格式证书,结果过程中报错了。网上类似资料比较少,做个记录。 生成pfx格式证书的命令: o…...

微信小程序 分享按钮 监听用户分享成功
代码 <view><button class"btnLq ed flex justify-center" open-type"share" click"getAward">点击分享</button> </view>export default {data(){return{shareMd:false,//分享埋点}},onShow(){//if(this.shareMd){uni.…...

数据结构-怀化学院期末题
题目: 利用希尔排序算法实现线性表的排序。希尔排序是根据给定的增量序列将线性表分隔成某个“增量”的记录组成一个子序例,在子序列中采用直接插入排序完成。 输入 第一行为元素个数n(1<n<1000),第二行为n个元素值(整数),即…...
跟cherno手搓游戏引擎【1】:配置与入口点
环境配置: 编译环境:VS2019 创建两个项目: 设置Sandbox为启动项: 设置sandbox的配置属性-常规-输出目录\中间目录为如下: 预处理定义:为了配置一些只有windows才能用的函数。 设置YOTOEngin(我…...
25计算机专业考研经验贴之准备篇
Hello各位小伙伴,大家新年好! 马上就要进入寒假假期了,25考研也该提上日程了。今天先跟大家分享一下大家在假期可以先做起来的准备工作。 【选择学校】 择校是个非常重要的内容,因为不同学校的考试内容是不一样的,有些…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
