算法通关村第二十关-黄金挑战图的常见算法
大家好我是苏麟 , 今天聊聊图的常见算法 .
图里的算法是很多的,这里我们介绍一些常见的图算法。这些算法一般都比较复杂,我们这里介绍这些算法的基本含义,适合面试的时候装*,如果手写,那就不用啦。
图分析算法,以图论为驱动,进行算法优化,结合应用工程,业务形态研究,不同领域场景模拟不同网络结构,通过自由刻画网络图形关系,验证结构合理性,如边的有向和无向及权重,从而辅助分析图形关系、图结构分析、网络结构分析等研究
1.最小生成树(Minimum Spanning Tree)
主要是三种算法: Prim算法、Kruskal算法、Sollin (Boruvka)算法
(1) Prim算法,普里姆算法,图论中的一种算法,基于一种贪心的思想,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语: Vertex(graph theory) 且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语: Voitech Jarnik)发现:并在1957年由美国计算机科学家罗伯特·普里姆英语: Robert C.Prim) 独立发现1959年,艾效格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆 - 亚尔尼克算法。Prime算法本质是动态规划

(2) Thorup 算法
对于平面有向图,一种更快的方法是如Mikkel Thorup在2004年所提出的算法。计算复杂度为,其中为增长速度非常缓慢的inverse-Ackermann函数。该算法还可以提供近似最短路径距离以及路由信息。
(3) Kameda算法
如果图形是平面的,非循环的,并且还表现出以下附加属性,则可以使用由1975年的T.Kameda 提出的更快的预处理方法: 所有0-indegree和所有0-outdegree顶点出现 (通常假设为外面),并且可以将该面的边界分割为两个部分,使得所有0个不等的顶点出现在一个部分上,并目所有的0度外的顶点出现在另一个部分上 (即两种类型的顶点不交替)。
2.连通结构 (Connected Components)
无向图G的极大连通子图称为G的连通分量( Connected Component)。任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。这种结构称作连通结构。

3.双联通结构 (Biconnected Components)
任意两点之间都有多于一条的路径,则称为双连通图,也叫双连通分量,双连通分量的术语是biconnectedcomponents,简称为BC,这种结构为双联通结构。任何一对顶点之间至少存在有两条路径,在删去某个顶点及与该顶点相关联的边时,也不破坏图的连通性。对于无向图的一个子图是双连通的,则称为双连通子图。极大的双连通子图称为双连通分量。一个无向图可以有多个双连通分量,一个点也算是双连通分量。

4.强联通结构 (Strongly Connected Components)
有向图的极大强连通子图称为的强连通分量,强连通图只有一个强连通分量,即是其自身。非强连通的有向图有多个强连通分量。如果任意两点之间都能到达,则称为强连通图。如果对于有向图的一个子图是强连通的,则称为强连通子图,这种结构称为强联通结构。

5.可达性 (Reachability)
在图论中,可达性是指在图中从一个顶点到另一个顶点的容易程度。在无向图中,可以通过识别图的连接分量来确定所有顶点对之间的可达性。我们的产品解决方案,通过定义一个实体为原点,通过原点链接计算出图中有向可达路径范围和无向可达路径范围,无向可达范围一般大于有向可达。

常用算法为: Floyd-Warshall,Thorup,Kameda这三种算法
(1) Floyd-Warshall算法
Floyd-Warshall算法(Floyd-Warshall algorithm) 是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Flovd-Warshal算法的时间复杂度为O(N)空间复杂度为O(N*N)。
(2) Thorup 算法
对于平面有向图,一种更快的方法是如Mikkel Thorup在2004年所提出的算法。计算复杂度为,其中为增长速度非常缓慢的inverse-Ackermann函数。该算法还可以提供近似最短路径距离以及路由信息。
(3) Kameda算法
如果图形是平面的,非循环的,并且还表现出以下附加属性,则可以使用由1975年的T.Kameda 提出的更快的预处理方法: 所有0-indegree和所有0-outdegree顶点出现 (通常假设为外面),并且可以将该面的边界分割为两人部分,使得所有0个不等的顶点出现在一个部分上,并且所有的0度外的顶点出现在另一个部分上 (即两种类型的顶点不交替)。
6.K核算法(K-Core)
k-Core算法是一种经典图算法,用于寻找一个图中符合指定核心度的顶点的集合,即要求每个顶点至少与该子图中的其他k个顶点相关联。k-Core算法用于寻找一个图中符合指定核心度的顶点的集合,求每个顶点至少与该子图中的其他k个顶点相关联。这个我们提供1-5Core的图计算,在图谱中可以分别找出1-5Core的团结果发现,并可以用于子图分类。适用于图推演、生物学、社交网络、金融风控等场景。

7.全路径 (ALL Paths)
全路径,就是网络图中的路径集合。分有向和无向,有向路径通过源到目标方向不可逆,无向路径通过源点和目标之间产生的图关系。在同一图形中,无向路径远多于有向。源点,是设定的初始点,目标是设置的需要通过源点要到达的点。有几种基本情况,一是源点和目标点同一设置,即自循环,有向情况下,自循环就是1个节点。二是无向情况下,自循环和有向情况一样,但二个节点以上则会多种混合循环体。产品可以通过设置源点和目标,进行分析源点和目标之间产生的有向无向关系。

8.链结构 (ALL Chains)
链结构,包含循环或路径,结构从图形结构树的基本循环集派生而来。通过优先搜索图形结构,把图中链分解成一组循环或路径,从原点出发有向或无向远离根原点后又回到原点则为基本环。如果没有回到原点则为一条路径而不是一个环。每个循环或路径称为链。这种结构称为链结构。

9.Single Source
Single Source,称为单源,意为只有一个源为基础。首先是不允许有负环,单源实体到所有实体的最短路径构成一棵最短路径树。通过单源路径算法可以通过选中实体定义源,找出以这个实体源为中心或起始点的图结果.

10.环结构 (Cycles)
环结构,即网络的循环结构,通过有向或无向路径最后,形成回到起点闭环。可以理解为形成一个“圈”。网络的基础循环是循环的最小集合,使得网络中的任何循环都可以写成基础中的循环总和。循环基数很有用,如单循环(自循环)、双向循环(双实体双向关系)、三角循环(三个实体循环路径) 、四方循环(四个实体循环路径)五边形以此类推。
还有很多 , 就不一一列举了 , 感兴趣的同学自己查查相关资料 .
这期就到这里了 , 再见!
相关文章:

算法通关村第二十关-黄金挑战图的常见算法
大家好我是苏麟 , 今天聊聊图的常见算法 . 图里的算法是很多的,这里我们介绍一些常见的图算法。这些算法一般都比较复杂,我们这里介绍这些算法的基本含义,适合面试的时候装*,如果手写,那就不用啦。 图分析算法…...

服务器内存不足怎么办?会有什么影响?
服务器内存,也被称为RAM(Random Access Memory),是一种临时存储设备,用于临时存放正在运行的程序和数据。它是服务器上的超高速存储介质,可以快速读取和写入数据,提供给CPU进行实时计算和操作。…...

GPT实战系列-简单聊聊LangChain
GPT实战系列-简单聊聊LangChain LLM大模型相关文章: GPT实战系列-ChatGLM3本地部署CUDA111080Ti显卡24G实战方案 GPT实战系列-Baichuan2本地化部署实战方案 GPT实战系列-大话LLM大模型训练 GPT实战系列-探究GPT等大模型的文本生成 GPT实战系列-Baichuan2等大模…...

【读书笔记】《白帽子讲web安全》浏览器安全
目录 第二篇 客户端脚本安全 第2章 浏览器安全 2.1同源策略 2.2浏览器沙箱 2.3恶意网址拦截 2.4高速发展的浏览器安全 第二篇 客户端脚本安全 第2章 浏览器安全 近年来随着互联网的发展,人们发现浏览器才是互联网最大的入口,绝大多数用户使用互联…...

海外服务器2核2G/4G/8G和4核8G配置16M公网带宽优惠价格表
腾讯云海外服务器租用优惠价格表,2核2G10M带宽、2核4G12M、2核8G14M、4核8G16M配置可选,可以选择Linux操作系统或Linux系统,相比较Linux服务器价格要更优惠一些,腾讯云服务器网txyfwq.com分享腾讯云国外服务器租用配置报价&#x…...

Linux 编译安装 Nginx
目录 一、前言二、四种安装方式介绍三、本文安装方式:源码安装3.1、安装依赖库3.2、开始安装 Nginx3.3、Nginx 相关操作3.4、把 Nginx 注册成系统服务 四、结尾 一、前言 Nginx 是一款轻量级的 Web 服务器、[反向代理]服务器,由于它的内存占用少…...
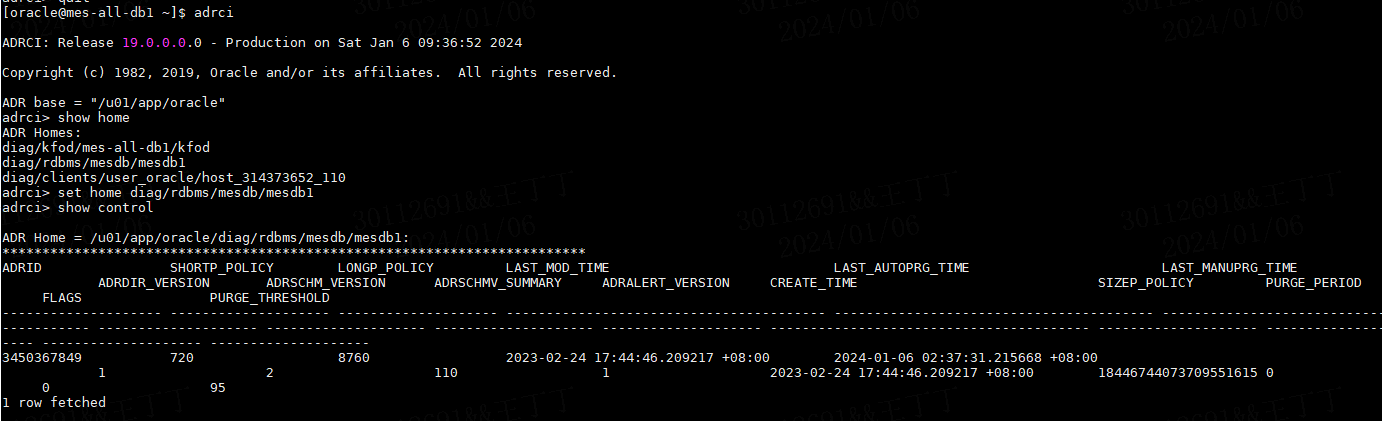
Oracle文件自动“减肥”记
📢📢📢📣📣📣 哈喽!大家好,我是【IT邦德】,江湖人称jeames007,10余年DBA及大数据工作经验 一位上进心十足的【大数据领域博主】!😜&am…...

【csharp】抽象类与接口有哪些不同?什么时候应该使用抽象类?
抽象类与接口有哪些不同? 抽象类和接口是在面向对象编程中两个不同的概念,它们有一些重要的区别。以下是抽象类和接口的主要不同点: 抽象类(Abstract Class): 成员类型: 抽象类可以包含抽象方…...

最新-mybatis-plus 3.5分页插件配置
mybatis-plus 3.5分页插件配置 前提 1.项目不是springboot, 是以前的常规spring项目 2.mp 从3.2升级到3.5,升级后发现原本的分页竟然不起作用了,每次查询都是查出所有 前后配置对比 jar包对比 jsqlparser我这里单独引了包,因为版本太低…...
案例098:基于微信小程序的电子购物系统的设计与实现
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

亚信安慧AntDB数据库:数字化时代的数据库创新引领者
AntDB数据库以其卓越的创新能力,集中体现在融合统一与实时处理两大关键领域。作为一款服务全国超过10亿用户的分布式数据库,其独特之处在于长期积累的经验、多样性的支持能力、快速响应的数据处理速度以及卓越的系统稳定性。AntDB不仅仅是一个数据库系统…...

【MySQL】关于日期转换的方法
力扣题 1、题目地址 1853. 转换日期格式 2、模拟表 表: Days Column NameTypedaydate day 是这个表的主键。 3、要求 给定一个Days表,请你编写SQL查询语句,将Days表中的每一个日期转化为"day_name, month_name day, year"格式的字符串…...
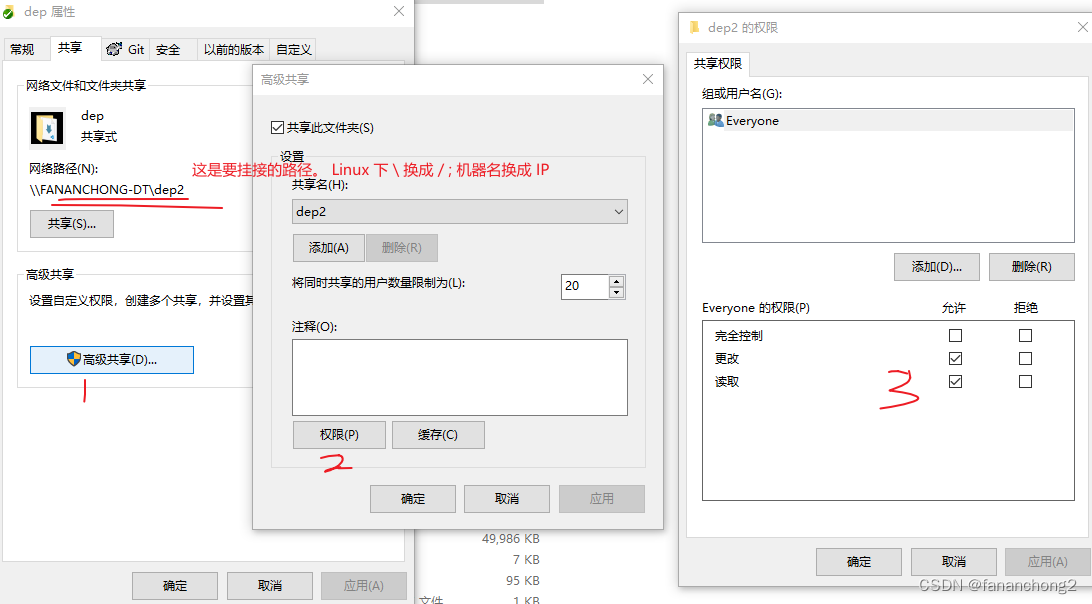
Ubuntu 虚拟机挂接 Windows 目录
Windows 共享目录 首先 Windows 下共享目录 我这里偷懒直接直接 Everyone ,也可以指定用户啥的 Ubuntu 挂接 挂接命令,类似如下: sudo mount -o usernamefananchong,passwordxxxx,uid1000,gid1000,file_mode0644,dir_mode0755,dynperm //…...
机器学习模型可解释性的结果分析
模型的可解释性是机器学习领域的一个重要分支,随着 AI 应用范围的不断扩大,人们越来越不满足于模型的黑盒特性,与此同时,金融、自动驾驶等领域的法律法规也对模型的可解释性提出了更高的要求,在可解释 AI 一文中我们已…...
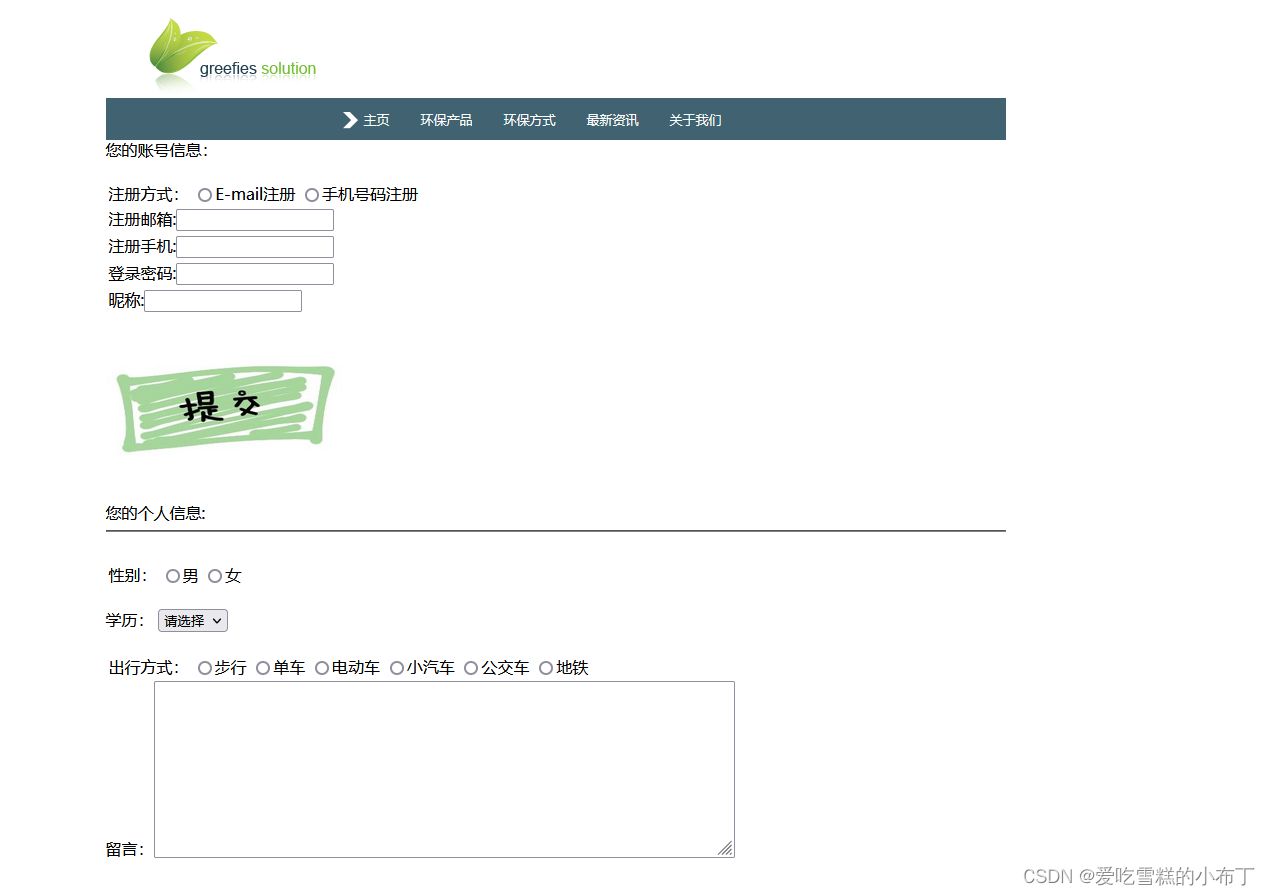
静态网页设计——环保网(HTML+CSS+JavaScript)(dw、sublime Text、webstorm、HBuilder X)
前言 声明:该文章只是做技术分享,若侵权请联系我删除。!! 感谢大佬的视频: https://www.bilibili.com/video/BV1BC4y1v7ZY/?vd_source5f425e0074a7f92921f53ab87712357b 使用技术:HTMLCSSJS(…...
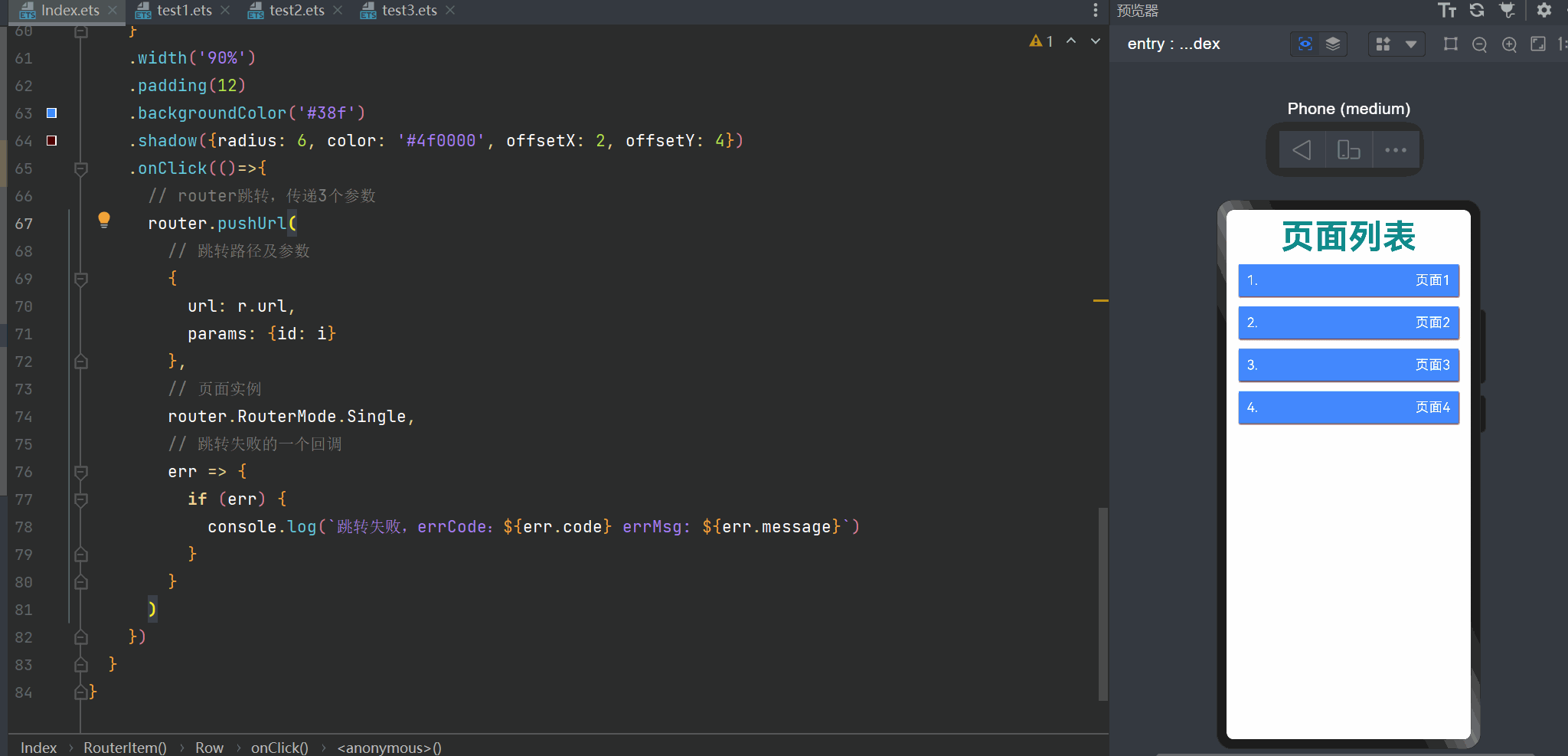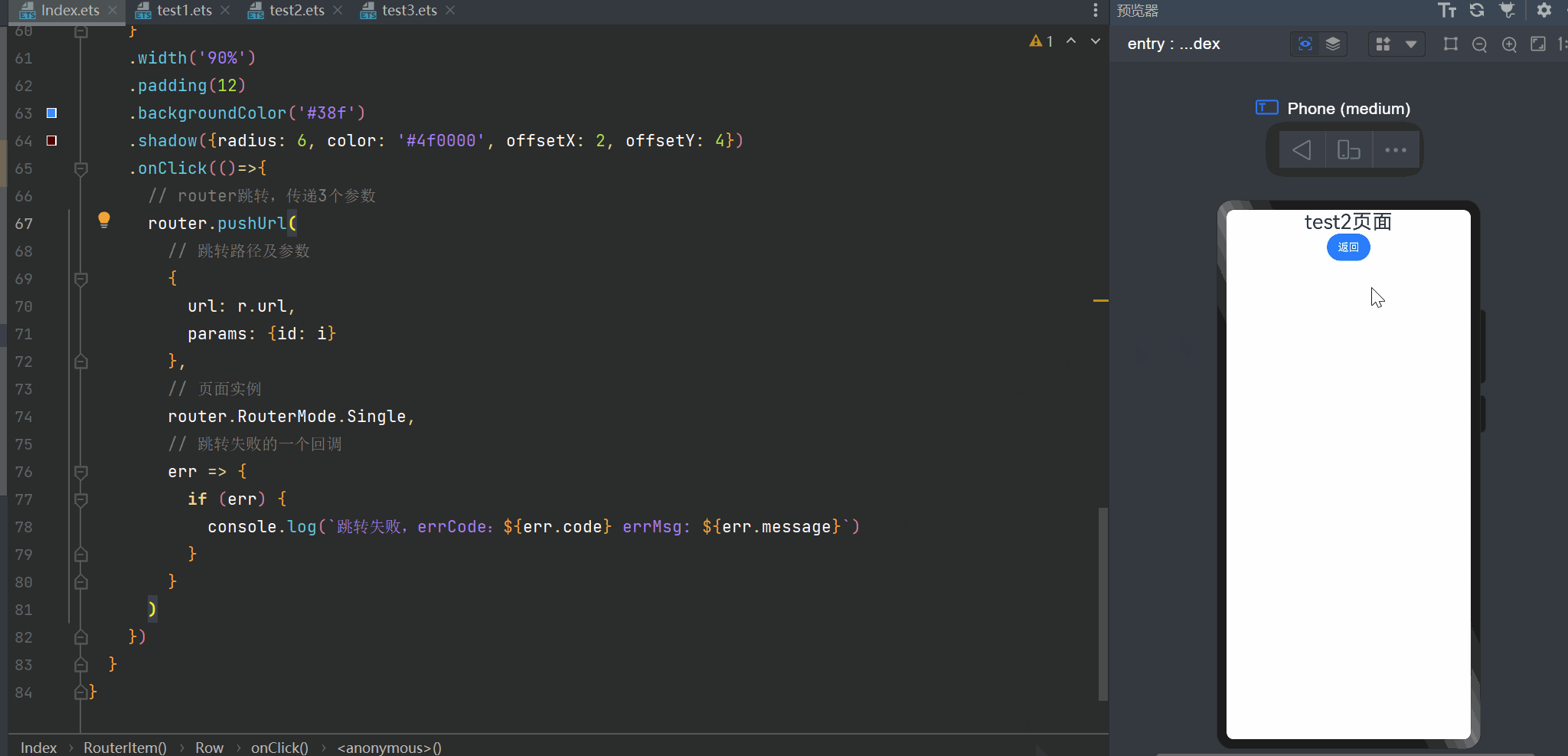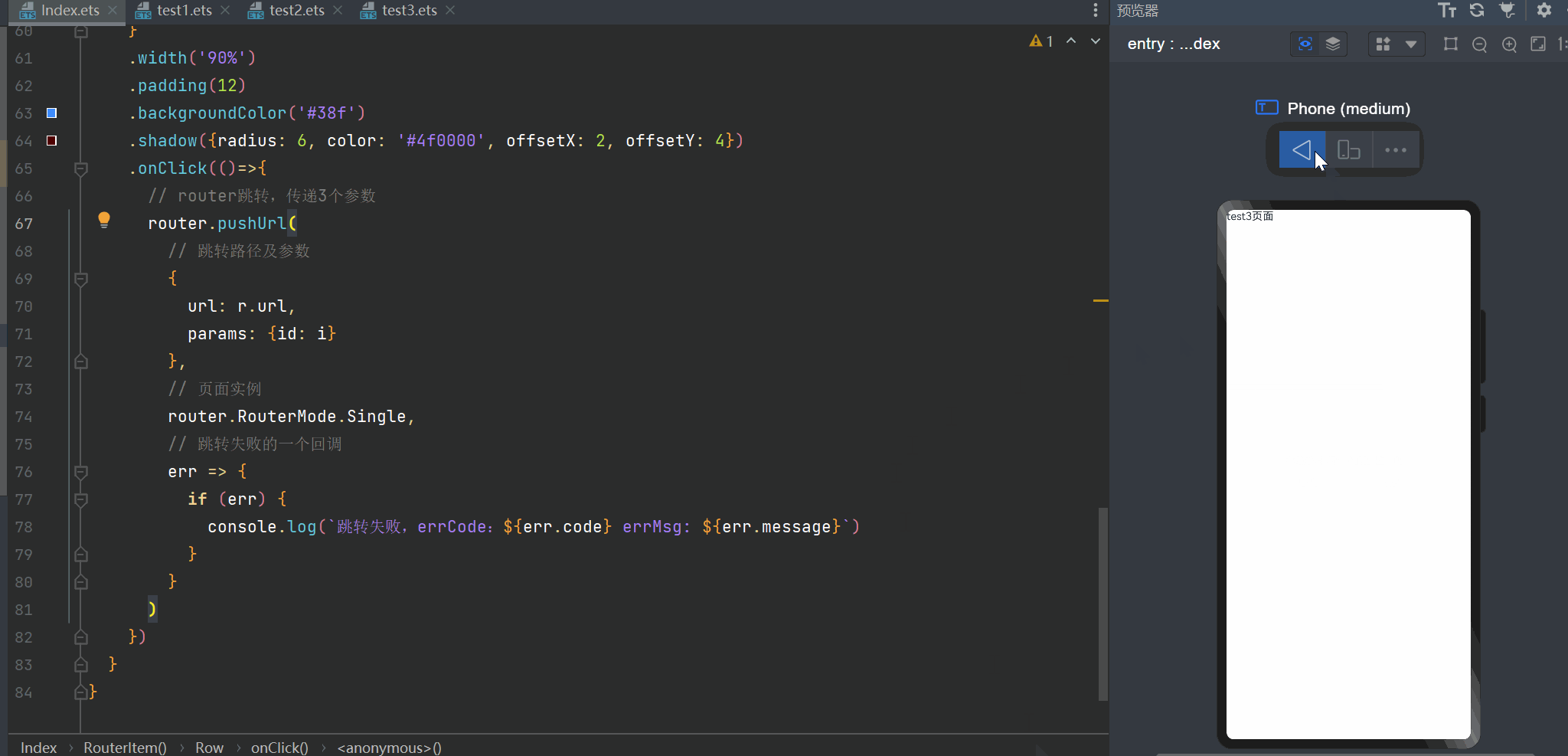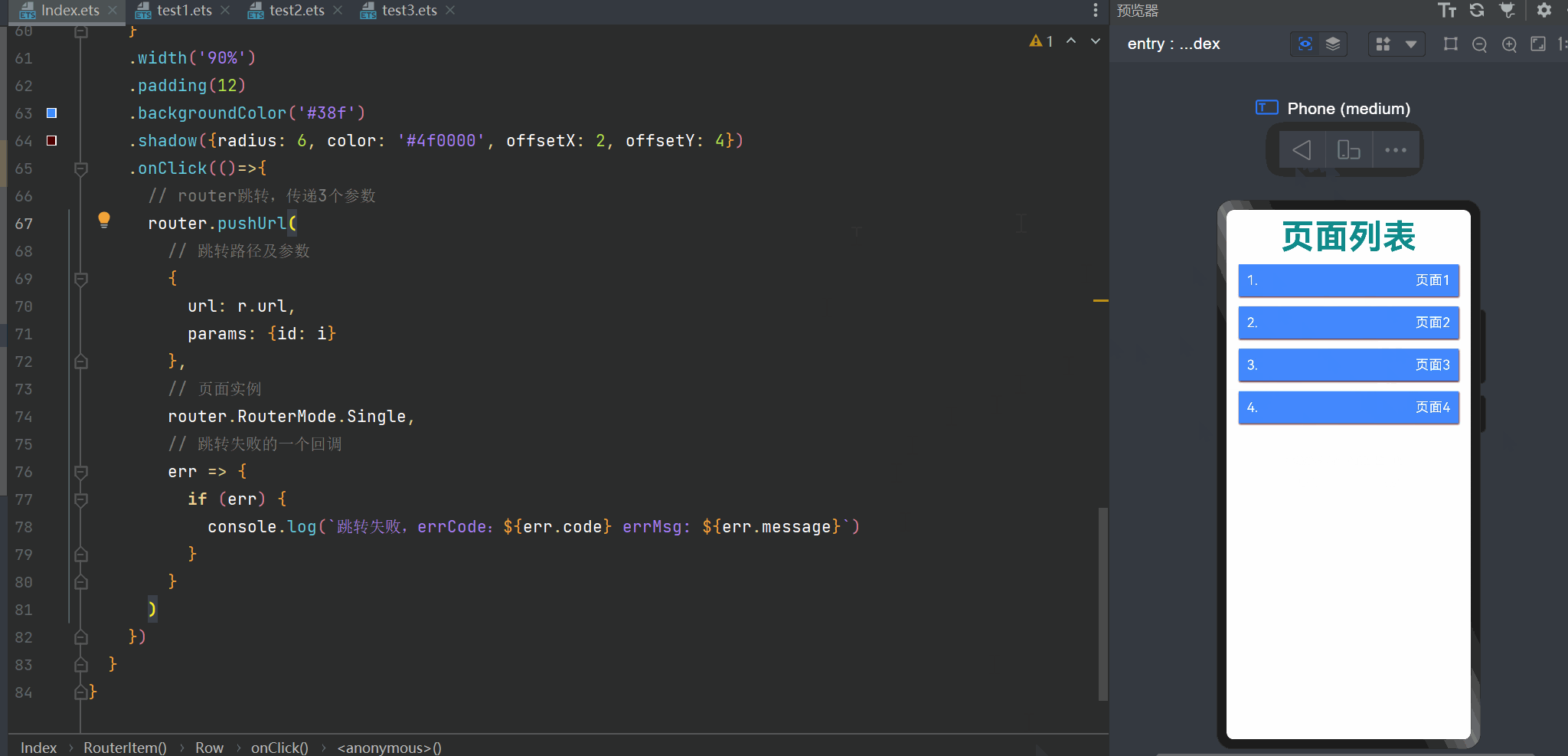
【HarmonyOS】装饰器下的状态管理与页面路由跳转实现
从今天开始,博主将开设一门新的专栏用来讲解市面上比较热门的技术 “鸿蒙开发”,对于刚接触这项技术的小伙伴在学习鸿蒙开发之前,有必要先了解一下鸿蒙,从你的角度来讲,你认为什么是鸿蒙呢?它出现的意义又是…...
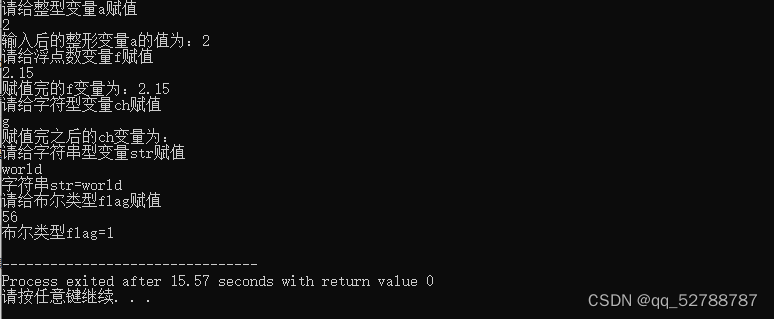
学习笔记——C++中数据的输入 cin
作用:用于从键盘中获取数据 关键字:cin 语法:cin>>变量 类型:C中数据的输入主要包含:整形(int)浮点型(float,double float),字符型&…...
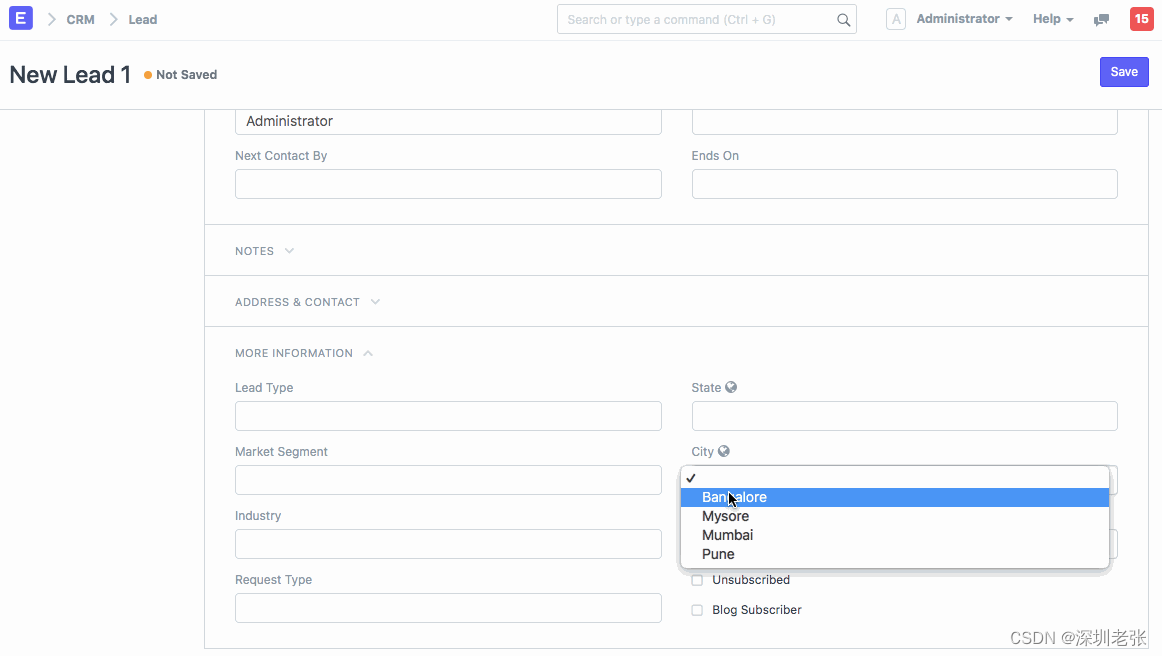
Filter Options in Select Field
Filter Options in Select Field 假设有两个下拉字段State和City。邦有两个值卡纳塔克邦和马哈拉施特拉邦,城市有四个值,班加罗尔,迈索尔,孟买和浦那。如果希望根据State中选择的值过滤City中的选项,可以编写如下所示的…...
【React系列】Hook(二)高级使用
本文来自#React系列教程:https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. Hook高级使用 1.1. useReducer 很多人看到useReducer的第一反应应该是redux的某个替代品,其实并不是…...

编程笔记 html5cssjs 018 HTML颜色
编程笔记 html5&css&js 018 HTML颜色 一、HTML 颜色二、HTML中设置颜色值三、颜色名称和颜色值 颜色是视觉中重要因素,尤其是处理人机界面中,更是要处理颜色设置和搭配。在网页中,提供了设置颜色的一些方案,需要我们认真学…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
