[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-2(3) 质量刚体的在坐标系下运动
本文仅供学习使用,总结很多本现有讲述运动学或动力学书籍后的总结,从矢量的角度进行分析,方法比较传统,但更易理解,并且现有的看似抽象方法,两者本质上并无不同。
2024年底本人学位论文发表后方可摘抄
若有帮助请引用
本文参考:
黎 旭,陈 强 洪,甄 文 强 等.惯 性 张 量 平 移 和 旋 转 复 合 变 换 的 一 般 形 式 及 其 应 用[J].工 程 数 学 学 报,2022,39(06):1005-1011.
食用方法
质量点的动量与角动量
刚体的动量与角动量——力与力矩的关系
惯性矩阵的表达与推导——在刚体运动过程中的作用
惯性矩阵在不同坐标系下的表达
机构运动学与动力学分析与建模 Ch00-2质量刚体的在坐标系下运动Part3
- 2.2.3 欧拉方程 Euler equation - 2
2.2.3 欧拉方程 Euler equation - 2
- 进而分析 H ⃗ Σ M F = m t o t a l ⋅ R ⃗ G F × V ⃗ G F + ∫ ( R ⃗ G P i F ⋅ R ⃗ G P i F ) ω ⃗ M F d m i − ∫ ( R ⃗ G P i F ⋅ ω ⃗ M F ) R ⃗ G P i F d m i \vec{H}_{\Sigma _{\mathrm{M}}}^{F}=m_{\mathrm{total}}\cdot \vec{R}_{\mathrm{G}}^{F}\times \vec{V}_{\mathrm{G}}^{F}+\int{\left( \vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}\cdot \vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F} \right) \vec{\omega}_{\mathrm{M}}^{F}}\mathrm{d}m_{\mathrm{i}}-\int{\left( \vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}\cdot \vec{\omega}_{\mathrm{M}}^{F} \right) \vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}}\mathrm{d}m_{\mathrm{i}} HΣMF=mtotal⋅RGF×VGF+∫(RGPiF⋅RGPiF)ωMFdmi−∫(RGPiF⋅ωMF)RGPiFdmi,有:
H ⃗ Σ M F = m t o t a l ⋅ R ⃗ G F × V ⃗ G F + ∫ ( R ⃗ G P i F T R ⃗ G P i F ⋅ E 3 × 3 − R ⃗ G P i F R ⃗ G P i F T ) d m i ⋅ ω ⃗ M F = m t o t a l ⋅ R ⃗ G F × V ⃗ G F + [ I ] Σ M / G F ⋅ ω ⃗ M F H ⃗ Σ M / G F = H ⃗ Σ M F − m t o t a l ⋅ R ⃗ G F × V ⃗ G F = [ I ] Σ M / G F ⋅ ω ⃗ M F \begin{split} &\vec{H}_{\Sigma _{\mathrm{M}}}^{F}=m_{\mathrm{total}}\cdot \vec{R}_{\mathrm{G}}^{F}\times \vec{V}_{\mathrm{G}}^{F}+\int{\left( {\vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}}^{\mathrm{T}}\vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}\cdot E^{3\times 3}-\vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}{\vec{R}_{\mathrm{GP}_{\mathrm{i}}}^{F}}^{\mathrm{T}} \right)}\mathrm{d}m_{\mathrm{i}}\cdot \vec{\omega}_{\mathrm{M}}^{F} =m_{\mathrm{total}}\cdot \vec{R}_{\mathrm{G}}^{F}\times \vec{V}_{\mathrm{G}}^{F}+\left[ I \right] _{\Sigma _{\mathrm{M}}/\mathrm{G}}^{F}\cdot \vec{\omega}_{\mathrm{M}}^{F} \\ &\vec{H}_{\Sigma _{\mathrm{M}}/\mathrm{G}}^{F}=\vec{H}_{\Sigma _{\mathrm{M}}}^{F}-m_{\mathrm{total}}\cdot \vec{R}_{\mathrm{G}}^{F}\times \vec{V}_{\mathrm{G}}^{F}=\left[ I \right] _{\Sigma _{\mathrm{M}}/\mathrm{G}}^{F}\cdot \vec{\omega}_{\mathrm{M}}^{F} \end{split} HΣMF=mtotal⋅RGF×VGF+∫(RGPiFTRGPiF⋅E3×3−RGPiFRGPiFT)dmi⋅ωMF=mtotal⋅RGF×VGF+[I]ΣM/GF⋅ωMFHΣM/GF=HΣMF−mtotal⋅RGF×VGF=[I]ΣM/GF⋅ωMF
则相对于质心点 G G G 存在:
{ τ ⃗ G F = d h ⃗ G F d t τ ⃗ G / O F = d h ⃗ G / O F d t + V ⃗ O F × P ⃗ G F P ⃗ G F = m t o t a l V ⃗ G F \begin{cases} \vec{\tau}_{\mathrm{G}}^{F}=\frac{\mathrm{d}\vec{h}_{\mathrm{G}}^{F}}{\mathrm{dt}}\\ \vec{\tau}_{\mathrm{G}/\mathrm{O}}^{F}=\frac{\mathrm{d}\vec{h}_{\mathrm{G}/\mathrm{O}}^{F}}{\mathrm{dt}}+\vec{V}_{\mathrm{O}}^{F}\times \vec{P}_{\mathrm{G}}^{F}\\ \vec{P}_{\mathrm{G}}^{F}=m_{\mathrm{total}}\vec{V}_{\mathrm{G}}^{F}\\ \end{cases} ⎩ ⎨ ⎧τGF=dtdhGFτG/OF=dtdhG/OF+VOF×PGFPGF=mtotalVGF - 对 H ⃗ Σ M / O F \vec{H}_{\Sigma _{\mathrm{M}}/\mathrm{O}}^{F} HΣM/OF进一步推导,可得:
H ⃗ Σ M / O F = ∑ i N R ⃗ O P i F × P ⃗ P i F = ∑ i N m P i ⋅ R ⃗ O P i F × ( ω ⃗ F × R ⃗ O P i F ) = ∑ i N m P i ⋅ R ⃗ ~ O P i F ⋅ ( ω ⃗ ~ F ⋅ R ⃗ O P i F ) = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ 0 − z O P i F y O P i F z O P i F 0 − x O P i F − y O P i F x O P i F 0 ] ⋅ [ I ^ J ^ K ^ ] T ( [ 0 − w z P i F w y P i F w z P i F 0 − w x P i F − w y P i F w x P i F 0 ] ⋅ [ x O P i F y O P i F z O P i F ] ) = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ [ ( y O P i F ) 2 + ( z O P i F ) 2 ] w x P i F − ( x O P i F y O P i F ) w y P i F − ( x O P i F z O P i F ) w z P i F − ( y O P i F x O P i F ) w x P i F + [ ( x O P i F ) 2 + ( z O P i F ) 2 ] w y P i F − ( y O P i F z O P i F ) w z P i F − ( z O P i F x O P i F ) w x P i F − ( z O P i F y O P i F ) w y P i F + [ ( x O P i F ) 2 + ( y O P i F ) 2 ] w z P i F ] = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ ( y O P i F ) 2 + ( z O P i F ) 2 − x O P i F y O P i F − x O P i F z O P i F − y O P i F x O P i F ( x O P i F ) 2 + ( z O P i F ) 2 − y O P i F z O P i F − z O P i F x O P i F − z O P i F y O P i F ( x O P i F ) 2 + ( y O P i F ) 2 ] [ w x P i F w y P i F w z P i F ] = [ I ^ J ^ K ^ ] T [ ∑ i N m P i ⋅ [ ( y O P i F ) 2 + ( z O P i F ) 2 ] − ∑ i N m P i ⋅ x O P i F y O P i F − ∑ i N m P i ⋅ ( x O P i F z O P i F ) − ∑ i N m P i ⋅ ( y O P i F x O P i F ) ∑ i N m P i ⋅ [ ( x O P i F ) 2 + ( z O P i F ) 2 ] − ∑ i N m P i ⋅ ( y O P i F z O P i F ) − ∑ i N m P i ⋅ ( z O P i F x O P i F ) − ∑ i N m P i ⋅ ( z O P i F y O P i F ) ∑ i N m P i ⋅ [ ( x O P i F ) 2 + ( y O P i F ) 2 ] ] [ w x P i F w y P i F w z P i F ] = [ I ^ J ^ K ^ ] T [ I x x I x y I x z I y x I y y I y z I z x I z y I z z ] [ w x P i F w y P i F w z P i F ] = [ I ^ J ^ K ^ ] T [ I x x w x P i F + I x y w y P i F + I x z w z P i F I y x w x P i F + I y y w y P i F + I y z w z P i F I z x w x P i F + I z y w y P i F + I z z w z P i F ] = [ I ^ J ^ K ^ ] T [ H x H y H z ] \begin{split} \vec{H}_{\Sigma _{\mathrm{M}}/\mathrm{O}}^{F}&=\sum_i^N{\vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F}\times \vec{P}_{\mathrm{P}_{\mathrm{i}}}^{F}}=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F}\times \left( \vec{\omega}^F\times \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \tilde{\vec{R}}_{\mathrm{OP}_{\mathrm{i}}}^{F}\cdot \left( \tilde{\vec{\omega}}^F\cdot \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{matrix} 0& -z_{\mathrm{OP}_{\mathrm{i}}}^{F}& y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ z_{\mathrm{OP}_{\mathrm{i}}}^{F}& 0& -x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ -y_{\mathrm{OP}_{\mathrm{i}}}^{F}& x_{\mathrm{OP}_{\mathrm{i}}}^{F}& 0\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left( \left[ \begin{matrix} 0& -w_{\mathrm{z}_{\mathrm{Pi}}}^{F}& w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}& 0& -w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ -w_{\mathrm{y}_{\mathrm{Pi}}}^{F}& w_{\mathrm{x}_{\mathrm{Pi}}}^{F}& 0\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \end{array} \right] \right)} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} \left[ \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right] w_{\mathrm{x}_{\mathrm{Pi}}}^{F}-\left( x_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{y}_{\mathrm{Pi}}}^{F}-\left( x_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ -\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+\left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right] w_{\mathrm{y}_{\mathrm{Pi}}}^{F}-\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ -\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{x}_{\mathrm{Pi}}}^{F}-\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+\left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right] w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right]} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{matrix} \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2& -x_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}& -x_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ -y_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}& \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2& -y_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ -z_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}& -z_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}& \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2\\ \end{matrix} \right] \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right]} \\ &=\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{matrix} \sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right]}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot x_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}\\ -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}& \sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right]}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}\\ -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}& \sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right]}\\ \end{matrix} \right] \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] \,\, \\ &=\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{matrix} I_{\mathrm{xx}}& I_{\mathrm{xy}}& I_{\mathrm{xz}}\\ I_{\mathrm{yx}}& I_{\mathrm{yy}}& I_{\mathrm{yz}}\\ I_{\mathrm{zx}}& I_{\mathrm{zy}}& I_{\mathrm{zz}}\\ \end{matrix} \right] \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] =\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} I_{\mathrm{xx}}w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+I_{\mathrm{xy}}w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+I_{\mathrm{xz}}w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ I_{\mathrm{yx}}w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+I_{\mathrm{yy}}w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+I_{\mathrm{yz}}w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ I_{\mathrm{zx}}w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+I_{\mathrm{zy}}w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+I_{\mathrm{zz}}w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] \\ &=\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} H_{\mathrm{x}}\\ H_{\mathrm{y}}\\ H_{\mathrm{z}}\\ \end{array} \right] \end{split} HΣM/OF=i∑NROPiF×PPiF=i∑NmPi⋅ROPiF×(ωF×ROPiF)=i∑NmPi⋅R~OPiF⋅(ω~F⋅ROPiF)=i∑NmPi⋅ I^J^K^ T 0zOPiF−yOPiF−zOPiF0xOPiFyOPiF−xOPiF0 ⋅ I^J^K^ T 0wzPiF−wyPiF−wzPiF0wxPiFwyPiF−wxPiF0 ⋅ xOPiFyOPiFzOPiF =i∑NmPi⋅ I^J^K^ T [(yOPiF)2+(zOPiF)2]wxPiF−(xOPiFyOPiF)wyPiF−(xOPiFzOPiF)wzPiF−(yOPiFxOPiF)wxPiF+[(xOPiF)2+(zOPiF)2]wyPiF−(yOPiFzOPiF)wzPiF−(zOPiFxOPiF)wxPiF−(zOPiFyOPiF)wyPiF+[(xOPiF)2+(yOPiF)2]wzPiF =i∑NmPi⋅ I^J^K^ T (yOPiF)2+(zOPiF)2−yOPiFxOPiF−zOPiFxOPiF−xOPiFyOPiF(xOPiF)2+(zOPiF)2−zOPiFyOPiF−xOPiFzOPiF−yOPiFzOPiF(xOPiF)2+(yOPiF)2 wxPiFwyPiFwzPiF = I^J^K^ T ∑iNmPi⋅[(yOPiF)2+(zOPiF)2]−∑iNmPi⋅(yOPiFxOPiF)−∑iNmPi⋅(zOPiFxOPiF)−∑iNmPi⋅xOPiFyOPiF∑iNmPi⋅[(xOPiF)2+(zOPiF)2]−∑iNmPi⋅(zOPiFyOPiF)−∑iNmPi⋅(xOPiFzOPiF)−∑iNmPi⋅(yOPiFzOPiF)∑iNmPi⋅[(xOPiF)2+(yOPiF)2] wxPiFwyPiFwzPiF = I^J^K^ T IxxIyxIzxIxyIyyIzyIxzIyzIzz wxPiFwyPiFwzPiF = I^J^K^ T IxxwxPiF+IxywyPiF+IxzwzPiFIyxwxPiF+IyywyPiF+IyzwzPiFIzxwxPiF+IzywyPiF+IzzwzPiF = I^J^K^ T HxHyHz
其中:
- 若有: ω ⃗ = [ I ^ J ^ K ^ ] T [ ω 1 ω 2 ω 3 ] , R ⃗ = [ I ^ J ^ K ^ ] T [ r 1 r 2 r 3 ] \vec{\omega}=\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} \omega _1\\ \omega _2\\ \omega _3\\ \end{array} \right] ,\vec{R}=\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} r_1\\ r_2\\ r_3\\ \end{array} \right] ω= I^J^K^ T ω1ω2ω3 ,R= I^J^K^ T r1r2r3 ,则有如下叉乘的计算:
ω ⃗ × R ⃗ = ω ⃗ ~ ⋅ R ⃗ = [ I ^ J ^ K ^ ] T ( [ 0 − ω 3 ω 2 ω 3 0 − ω 1 − ω 2 ω 1 0 ] ⋅ [ r 1 r 2 r 3 ] ) \vec{\omega}\times \vec{R}=\tilde{\vec{\omega}}\cdot \vec{R}=\left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left( \left[ \begin{matrix} 0& -\omega _3& \omega _2\\ \omega _3& 0& -\omega _1\\ -\omega _2& \omega _1& 0\\ \end{matrix} \right] \cdot \left[ \begin{array}{c} r_1\\ r_2\\ r_3\\ \end{array} \right] \right) ω×R=ω~⋅R= I^J^K^ T 0ω3−ω2−ω30ω1ω2−ω10 ⋅ r1r2r3 - H ⃗ Σ M / O F \vec{H}_{\Sigma _{\mathrm{M}}/\mathrm{O}}^{F} HΣM/OF表示刚体 Σ M \Sigma _{\mathrm{M}} ΣM
相对于(with respect to/W.R.T)点 O O O 的角动量在固定坐标系 { F } \left\{ F \right\} {F}的表达。其投影分量满足:
[ H x H y H z ] = [ I x x w x P i F + I x y w y P i F + I x z w z P i F I y x w x P i F + I y y w y P i F + I y z w z P i F I z x w x P i F + I z y w y P i F + I z z w z P i F ] = [ I x x I x y I x z I y x I y y I y z I z x I z y I z z ] [ w x P i F w y P i F w z P i F ] = [ I ] [ w x P i F w y P i F w z P i F ] \left[ \begin{array}{c} H_{\mathrm{x}}\\ H_{\mathrm{y}}\\ H_{\mathrm{z}}\\ \end{array} \right] =\left[ \begin{array}{c} I_{\mathrm{xx}}w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+I_{\mathrm{xy}}w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+I_{\mathrm{xz}}w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ I_{\mathrm{yx}}w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+I_{\mathrm{yy}}w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+I_{\mathrm{yz}}w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ I_{\mathrm{zx}}w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+I_{\mathrm{zy}}w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+I_{\mathrm{zz}}w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] =\left[ \begin{matrix} I_{\mathrm{xx}}& I_{\mathrm{xy}}& I_{\mathrm{xz}}\\ I_{\mathrm{yx}}& I_{\mathrm{yy}}& I_{\mathrm{yz}}\\ I_{\mathrm{zx}}& I_{\mathrm{zy}}& I_{\mathrm{zz}}\\ \end{matrix} \right] \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] =\left[ I \right] \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] HxHyHz = IxxwxPiF+IxywyPiF+IxzwzPiFIyxwxPiF+IyywyPiF+IyzwzPiFIzxwxPiF+IzywyPiF+IzzwzPiF = IxxIyxIzxIxyIyyIzyIxzIyzIzz wxPiFwyPiFwzPiF =[I] wxPiFwyPiFwzPiF - 矩阵 [ I ] \left[ I \right] [I]常被称为
{惯性矩阵Inertia-matrix,有: H ⃗ Σ M / O F = [ I ] ω ⃗ F \vec{H}_{\Sigma _{\mathrm{M}}/\mathrm{O}}^{F}=\left[ I \right] \vec{\omega}^F HΣM/OF=[I]ωF,其中:
[ I ] = [ I x x I x y I x z I y x I y y I y z I z x I z y I z z ] = [ ∑ i N m P i ⋅ [ ( y O P i F ) 2 + ( z O P i F ) 2 ] − ∑ i N m P i ⋅ x O P i F y O P i F − ∑ i N m P i ⋅ ( x O P i F z O P i F ) − ∑ i N m P i ⋅ ( y O P i F x O P i F ) ∑ i N m P i ⋅ [ ( x O P i F ) 2 + ( z O P i F ) 2 ] − ∑ i N m P i ⋅ ( y O P i F z O P i F ) − ∑ i N m P i ⋅ ( z O P i F x O P i F ) − ∑ i N m P i ⋅ ( z O P i F y O P i F ) ∑ i N m P i ⋅ [ ( x O P i F ) 2 + ( y O P i F ) 2 ] ] \begin{split} \left[ I \right] &=\left[ \begin{matrix} I_{\mathrm{xx}}& I_{\mathrm{xy}}& I_{\mathrm{xz}}\\ I_{\mathrm{yx}}& I_{\mathrm{yy}}& I_{\mathrm{yz}}\\ I_{\mathrm{zx}}& I_{\mathrm{zy}}& I_{\mathrm{zz}}\\ \end{matrix} \right] \\ &=\left[ \begin{matrix} \sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right]}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot x_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}\\ -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}& \sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right]}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}\\ -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}& -\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}& \sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right]}\\ \end{matrix} \right] \end{split} [I]= IxxIyxIzxIxyIyyIzyIxzIyzIzz = ∑iNmPi⋅[(yOPiF)2+(zOPiF)2]−∑iNmPi⋅(yOPiFxOPiF)−∑iNmPi⋅(zOPiFxOPiF)−∑iNmPi⋅xOPiFyOPiF∑iNmPi⋅[(xOPiF)2+(zOPiF)2]−∑iNmPi⋅(zOPiFyOPiF)−∑iNmPi⋅(xOPiFzOPiF)−∑iNmPi⋅(yOPiFzOPiF)∑iNmPi⋅[(xOPiF)2+(yOPiF)2]
上式的实际推导过程,是进行两次转置变化,在实际过程中可以理解成,适用于矩阵与矢量相乘的张量Tensor乘法,因此也可将惯性矩阵 [ I ] \left[ I \right] [I]称为惯性张量Inertia Tensor。而采用基于拉格朗日恒等式证明的三个向量的双重矢积公式,可能更利于理解:
- 三个向量的双重矢积公式: ( r ⃗ 1 × r ⃗ 2 ) × r ⃗ 3 = ( r ⃗ 1 ⋅ r ⃗ 3 ) r ⃗ 2 − ( r ⃗ 2 ⋅ r ⃗ 3 ) r ⃗ 1 \left( \vec{r}_1\times \vec{r}_2 \right) \times \vec{r}_3=\left( \vec{r}_1\cdot \vec{r}_3 \right) \vec{r}_2-\left( \vec{r}_2\cdot \vec{r}_3 \right) \vec{r}_1 (r1×r2)×r3=(r1⋅r3)r2−(r2⋅r3)r1
H ⃗ Σ M / O F = ∑ i N R ⃗ O P i F × P ⃗ P i F = ∑ i N m P i ⋅ R ⃗ O P i F × ( ω ⃗ F × R ⃗ O P i F ) = ∑ i N m P i ⋅ [ ( R ⃗ O P i F ⋅ R ⃗ O P i F ) ω ⃗ F − ( ω ⃗ F ⋅ R ⃗ O P i F ) R ⃗ O P i F ] = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ ( [ x O P i F y O P i F z O P i F ] T [ x O P i F y O P i F z O P i F ] ) [ w x P i F w y P i F w z P i F ] − ( [ w x P i F w y P i F w z P i F ] T [ x O P i F y O P i F z O P i F ] ) [ x O P i F y O P i F z O P i F ] ] = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ [ ( ( x O P i F ) 2 + ( y O P i F ) 2 + ( z O P i F ) 2 ) w x P i F ( ( x O P i F ) 2 + ( y O P i F ) 2 + ( z O P i F ) 2 ) w y P i F ( ( x O P i F ) 2 + ( y O P i F ) 2 + ( z O P i F ) 2 ) w z P i F ] − [ ( w x P i F x O P i F + w y P i F y O P i F + w z P i F z O P i F ) x O P i F ( w x P i F x O P i F + w y P i F y O P i F + w z P i F z O P i F ) y O P i F ( w x P i F x O P i F + w y P i F y O P i F + w z P i F z O P i F ) z O P i F ] ] = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ [ ( y O P i F ) 2 + ( z O P i F ) 2 ] w x P i F − ( x O P i F y O P i F ) w y P i F − ( x O P i F z O P i F ) w z P i F − ( y O P i F x O P i F ) w x P i F + [ ( x O P i F ) 2 + ( z O P i F ) 2 ] w y P i F − ( y O P i F z O P i F ) w z P i F − ( z O P i F x O P i F ) w x P i F − ( z O P i F y O P i F ) w y P i F + [ ( x O P i F ) 2 + ( y O P i F ) 2 ] w z P i F ] = ∑ i N m P i ⋅ [ I ^ J ^ K ^ ] T [ ( y O P i F ) 2 + ( z O P i F ) 2 − x O P i F y O P i F − x O P i F z O P i F − y O P i F x O P i F ( x O P i F ) 2 + ( z O P i F ) 2 − y O P i F z O P i F − z O P i F x O P i F − z O P i F y O P i F ( x O P i F ) 2 + ( y O P i F ) 2 ] [ w x P i F w y P i F w z P i F ] \begin{split} \vec{H}_{\Sigma _{\mathrm{M}}/\mathrm{O}}^{F}&=\sum_i^N{\vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F}\times \vec{P}_{\mathrm{P}_{\mathrm{i}}}^{F}}=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F}\times \left( \vec{\omega}^F\times \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F} \right)}=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \left( \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F}\cdot \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) \vec{\omega}^F-\left( \vec{\omega}^F\cdot \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) \vec{R}_{\mathrm{OP}_{\mathrm{i}}}^{F} \right]} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \left( \left[ \begin{array}{c} x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \end{array} \right] \right) \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] -\left( \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \end{array} \right] \right) \left[ \begin{array}{c} x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \end{array} \right] \right]} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \left[ \begin{array}{c} \left( \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right) w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ \left( \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right) w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ \left( \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right) w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] -\left[ \begin{array}{c} \left( w_{\mathrm{x}_{\mathrm{Pi}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}+w_{\mathrm{y}_{\mathrm{Pi}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}+w_{\mathrm{z}_{\mathrm{Pi}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) x_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \left( w_{\mathrm{x}_{\mathrm{Pi}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}+w_{\mathrm{y}_{\mathrm{Pi}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}+w_{\mathrm{z}_{\mathrm{Pi}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) y_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \left( w_{\mathrm{x}_{\mathrm{Pi}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}+w_{\mathrm{y}_{\mathrm{Pi}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}+w_{\mathrm{z}_{\mathrm{Pi}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ \end{array} \right] \right]} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}\left[ \begin{array}{c} \left[ \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right] w_{\mathrm{x}_{\mathrm{Pi}}}^{F}-\left( x_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{y}_{\mathrm{Pi}}}^{F}-\left( x_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ -\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{x}_{\mathrm{Pi}}}^{F}+\left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right] w_{\mathrm{y}_{\mathrm{Pi}}}^{F}-\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ -\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{x}_{\mathrm{Pi}}}^{F}-\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) w_{\mathrm{y}_{\mathrm{Pi}}}^{F}+\left[ \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2 \right] w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right]} \\ &=\sum_i^N{m_{\mathrm{P}_{\mathrm{i}}}\cdot \left[ \begin{array}{c} \hat{I}\\ \hat{J}\\ \hat{K}\\ \end{array} \right] ^{\mathrm{T}}}\left[ \begin{matrix} \left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2& -x_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}& -x_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ -y_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}& \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( z_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2& -y_{\mathrm{OP}_{\mathrm{i}}}^{F}z_{\mathrm{OP}_{\mathrm{i}}}^{F}\\ -z_{\mathrm{OP}_{\mathrm{i}}}^{F}x_{\mathrm{OP}_{\mathrm{i}}}^{F}& -z_{\mathrm{OP}_{\mathrm{i}}}^{F}y_{\mathrm{OP}_{\mathrm{i}}}^{F}& \left( x_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2+\left( y_{\mathrm{OP}_{\mathrm{i}}}^{F} \right) ^2\\ \end{matrix} \right] \left[ \begin{array}{c} w_{\mathrm{x}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{y}_{\mathrm{Pi}}}^{F}\\ w_{\mathrm{z}_{\mathrm{Pi}}}^{F}\\ \end{array} \right] \end{split} HΣM/OF=i∑NROPiF×PPiF=i∑NmPi⋅ROPiF×(ωF×ROPiF)=i∑NmPi⋅[(ROPiF⋅ROPiF)ωF−(ωF⋅ROPiF)ROPiF]=i∑NmPi⋅ I^J^K^ T xOPiFyOPiFzOPiF T xOPiFyOPiFzOPiF wxPiFwyPiFwzPiF − wxPiFwyPiFwzPiF T xOPiFyOPiFzOPiF xOPiFyOPiFzOPiF =i∑NmPi⋅ I^J^K^ T ((xOPiF)2+(yOPiF)2+(zOPiF)2)wxPiF((xOPiF)2+(yOPiF)2+(zOPiF)2)wyPiF((xOPiF)2+(yOPiF)2+(zOPiF)2)wzPiF − (wxPiFxOPiF+wyPiFyOPiF+wzPiFzOPiF)xOPiF(wxPiFxOPiF+wyPiFyOPiF+wzPiFzOPiF)yOPiF(wxPiFxOPiF+wyPiFyOPiF+wzPiFzOPiF)zOPiF =i∑NmPi⋅ I^J^K^ T [(yOPiF)2+(zOPiF)2]wxPiF−(xOPiFyOPiF)wyPiF−(xOPiFzOPiF)wzPiF−(yOPiFxOPiF)wxPiF+[(xOPiF)2+(zOPiF)2]wyPiF−(yOPiFzOPiF)wzPiF−(zOPiFxOPiF)wxPiF−(zOPiFyOPiF)wyPiF+[(xOPiF)2+(yOPiF)2]wzPiF =i∑NmPi⋅ I^J^K^ T (yOPiF)2+(zOPiF)2−yOPiFxOPiF−zOPiFxOPiF−xOPiFyOPiF(xOPiF)2+(zOPiF)2−zOPiFyOPiF−xOPiFzOPiF−yOPiFzOPiF(xOPiF)2+(yOPiF)2 wxPiFwyPiFwzPiF
相关文章:
 质量刚体的在坐标系下运动)
[足式机器人]Part3 机构运动学与动力学分析与建模 Ch00-2(3) 质量刚体的在坐标系下运动
本文仅供学习使用,总结很多本现有讲述运动学或动力学书籍后的总结,从矢量的角度进行分析,方法比较传统,但更易理解,并且现有的看似抽象方法,两者本质上并无不同。 2024年底本人学位论文发表后方可摘抄 若有…...

云计算历年题整理
目录 第一大题 第一大题HA计算 给出计算连接到EC2节点的EBS的高可用性(HA)的数学公式,如场景中所述;计算EC2节点上的EBS的高可用性(HA);场景中80%的AWS EC2节点用于并行处理,总共有100个虚拟中央处理单元(vCPUs)用于处理数据&a…...

2401vim,vim重要修改更新大全
原文 2023 更好的UTF-16支持 添加strutf16len()和utf16idx(),并在byteidx(),byteidxcomp()和charidx()中添加utf16标志,在内置.txt文档中. 添加crypymethod xchacha20v2 与xchacha20基本相同,但更能抵御libsodium的变化. 2022 添加"smoothscroll" 用鼠标滚动…...

安卓多用户管理之Userinfo
目录 前言Userinfo----用户信息1.1 属性1.2 构造器1.3 信息的判断及获取方法1.3.1 获取默认用户类型1.3.2 基础信息判断 1.4 序列化部分 总结 前言 UserManagerService内部类UserData中有一个Userinfo类型的info参数,在UserData中并未有所体现,但在后续…...

JavaScript-流程控制-笔记
1.流程语句的分类 顺序结构 分支结构 循环结构 2.if语句 1)if结构 if( 条件 ){ // 条件成立执行的代码 } 2)if else 结构 if( 条件 ){ // 条件成立执行的代码 }else{ // 条件不成…...

springboot + vue3实现增删改查分页操作
springboot vue3实现增删改查分页操作 环境最终实现效果实现功能主要框架代码实现数据库后端前端 注意事项 环境 jdk17 vue3 最终实现效果 实现功能 添加用户,禁用,启用,删除,编辑,分页查询 主要框架 后端 spri…...

leetcode01-重复的子字符串
题目链接:459. 重复的子字符串 - 力扣(LeetCode) 一般思路: 如果存在k是S的字串,记k的长度为s,S的长度为n,则一定有n是s的倍数,且满足对于j∈[s,n],一定存在s[j]s[j-s]; …...

目标检测数据集 - 夜间行人检测数据集下载「包含VOC、COCO、YOLO三种格式」
数据集介绍:夜间、低光行人检测数据集,真实场景高质量图片数据,涉及场景丰富,比如夜间街景行人、夜间道路行人、夜间遮挡行人、夜间严重遮挡行人数据;适用实际项目应用:公共场所监控场景下夜间行人检测项目…...
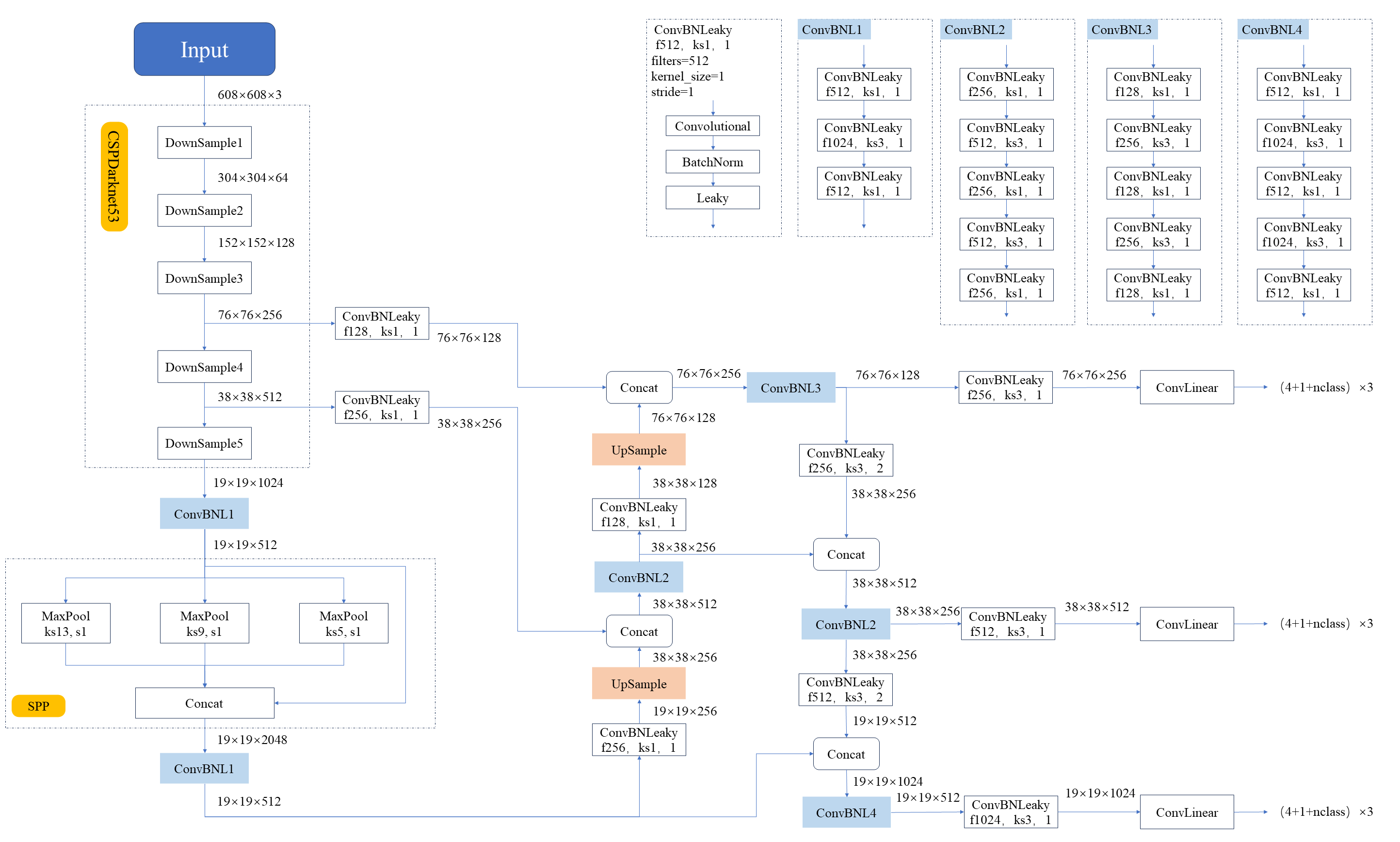
【YOLO系列】 YOLOv4思想详解
前言 以下内容仅为个人在学习人工智能中所记录的笔记,先将目标识别算法yolo系列的整理出来分享给大家,供大家学习参考。 本文未对论文逐句逐段翻译,而是阅读全文后,总结出的YOLO V4论文的思路与实现路径。 若文中内容有误…...
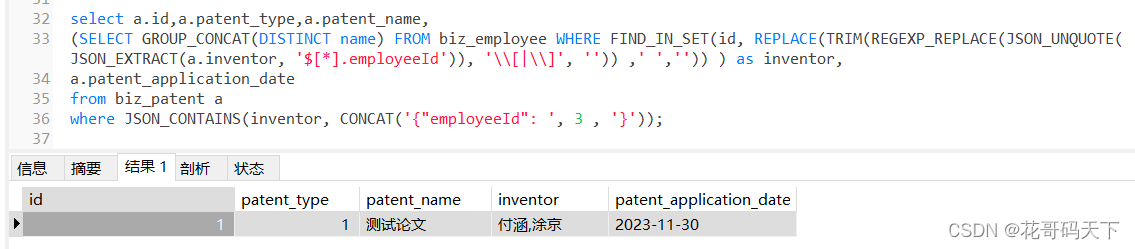
查询json数组
步骤一:创建表格 首先,我们需要创建一个表格来存储包含JSON对象数组的数据。可以使用以下代码创建一个名为 my_table 的表格: CREATE TABLE my_table (id INT PRIMARY KEY AUTO_INCREMENT,json_data JSON ); 上述代码创建了一个包含两个列的…...
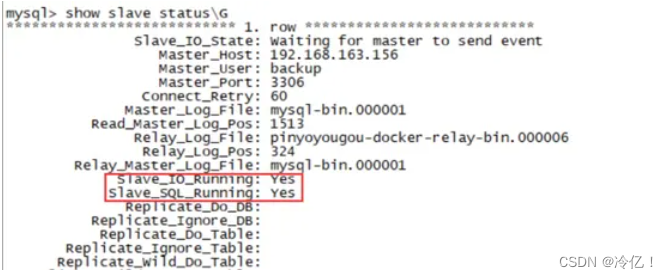
Docker mysql 主从复制
目录 介绍:为什么需要进行mysql的主从复制 主从复制原理: ✨主从环境搭建 主从一般面试问题: 介绍:为什么需要进行mysql的主从复制 在实际的生产中,为了解决Mysql的单点故障已经提高MySQL的整体服务性能ÿ…...
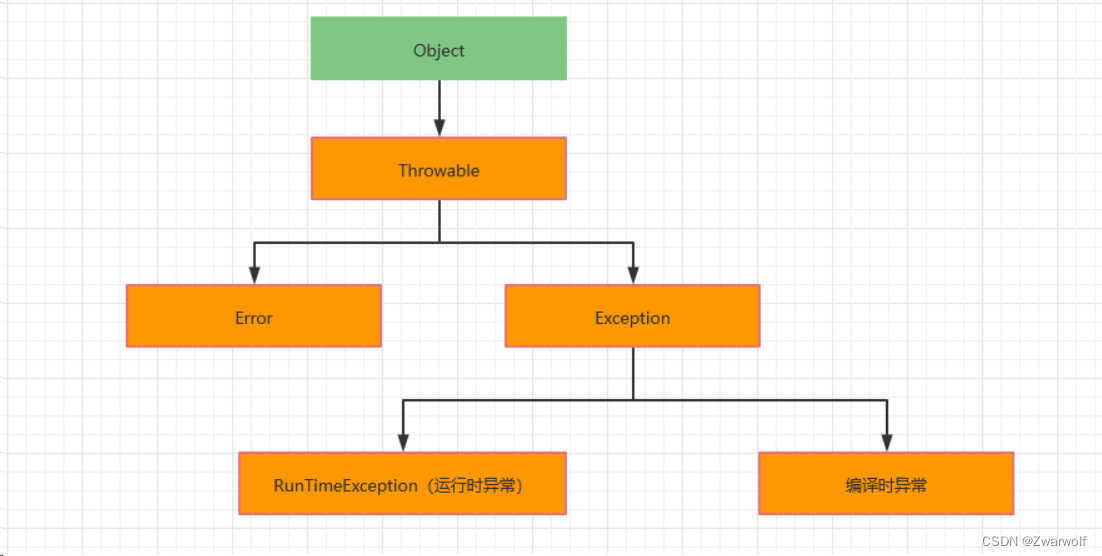
第7章-第1节-Java中的异常处理
1、异常Exception概述: 1)、异常的概念: 现实生活中万物在发展和变化会出现各种各样不正常的现象。 例如:人的成长过程中会生病。 实际工作中,遇到的情况不可能是非常完美的。 比如:你写的某个模块&…...

使用python生成一个月度账单消费金额柱状图表
阿里云月度账单根据月份、消费金额(可开票)生成一个柱状图表 import pandas as pd import matplotlib.pyplot as plt import os# 设置中文字体 plt.rcParams[font.sans-serif] [SimHei] # 用于显示中文的宋体# 获取当前工作目录下所有CSV文件 csv_fil…...

将一个独立的磁盘添加到已有的 `/` 分区
将一个独立的磁盘添加到已有的 / 分区是比较复杂的,因为 / 分区已经是一个逻辑卷(LVM)。在这种情况下,可以扩展现有的 LVM 体积组(Volume Group),然后扩展 / 逻辑卷(Logical Volume&…...

AI智能电销器人需要注意哪些问题呢
随着科技的不断发展,人们出行变得越来越方便,市面上很多产品也越来越智能化,高科技的产品不仅改变了我们的生活方式而且也改变了企业的竞争方式,很多的企业尤其是电销行业中的大佬己经意识到了AI电销机器人的好处,因此…...

呼叫中心研究分析:到2027年市场规模预计将达4966亿美元
由于业务运营中以客户为中心的方法的兴起,呼叫中心市场近年来出现了显着增长。随着对客户满意度的日益重视,全球对呼叫中心服务的需求猛增。在本次分析中,我们将从全球和中国的角度审视呼叫中心市场的发展趋势。全球市场: 到 2027…...

工业数据采集分析——工厂大脑 提升综合经济效益
随着企业对数字化的认知越来越清晰,对工业数智化的战略越来越明确,企业的诉求也在发生转变。中国的工业企业经过近几十年的发展,自动化、信息化,以及一些基础的数据系统建设在不同的行业中慢慢地推进。近几年,工业企业…...

python系列教程218——生成器表达式
朋友们,如需转载请标明出处:https://blog.csdn.net/jiangjunshow 声明:在人工智能技术教学期间,不少学生向我提一些python相关的问题,所以为了让同学们掌握更多扩展知识更好地理解AI技术,我让助理负责分享…...

jquery 实现简单的标签页效果
实现 <!DOCTYPE html> <html> <head><title>jq 实现简单的标签页效果</title><script src"/jquery/jquery-1.11.1.min.js"></script><style>.tab {cursor: pointer;width:100px;height:30px;float:left;text-align…...

C++ Web框架Drogon初体验笔记
这段时间研究了一下C的Web框架Drogon。从设计原理上面来说和Python的Web框架是大同小异的,但是难点在于编译项目上面,所以现在记录一下编译的过程。下面图是我项目的目录。其中include放的是头文件,src放的是视图文件,static放的是…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
