贪心算法的“左最优“与“右最优“及其对应的堆处理和预处理方法
1 答疑
1.1 什么是贪心算法的"左最优"与"右最优"
"左最优"和"右最优"是贪心算法中的两种策略:
-
左最优 (Leftmost Greedy): 在每一步选择中,总是选择最左边(最早出现的)可行的选项。
-
右最优 (Rightmost Greedy): 在每一步选择中,总是选择最右边(最晚出现的)可行的选项。
这两种策略是贪心算法中根据具体问题选择的不同方向。
1.2 这两种最优问题,分别用什么方法解决?
一般左最优可以采取边遍历边找出"当前的最值", 右最优不能向左最优一样通过左到右的遍历稍带最值,所以一般需要预处理从右到左遍历并且将得到的最值存放到数组中。
2 “左最优” 类题目
左最优其实也是一种局部最优
2.1 字节笔试题
小明在玩一场通关游戏,初始血量为1,关卡有怪兽或者有血包(正数就是血包可回血数,负数说明是怪兽的伤害值),当捡到血包时会加血量,碰到怪兽时会掉血,现在指定初始血量为x,关卡是一个数组,小明必须按照数组的顺序玩游戏,当碰到一个怪兽时,他可以选择将这个怪兽扔到数组末尾,小明可以无限次地将怪兽移到数组末尾,问小明最少移动几次就能存活,如果无论怎么移动都不能存活则返回-1, 假设关卡是这样的[-200,-300,400],则返回-1,假如是这样的[200,100,-250,-60,-70,100],则返回1,只需要把-250挪到尾部,
思路:当发现自己血量不足时,就从当前已经遍历过的所有关卡中,选择耗费血量最多的那个关卡并且放到最后一关,如果即使这样挪开了耗血量最大的一关自身血量还是为负,则直接返回-1,说明无法通关
———————————————— 版权声明:本文为CSDN博主「xxx_520s」的原创文章,遵循CC 4.0
BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/yxg520s/article/details/131989933
2.2 leetcode 1642. 可以到达的最远建筑
这样的贪心思路,871题最低加油次数和630课程表III也有体现。
两种贪心策略均可:
优先使用梯子,梯子不够时选取差值最小的出堆改用砖头。(小根堆)
优先使用砖头,砖头不够时选取消耗最大的出堆改用梯子。(大根堆)
解法一的理论复杂度应该是最低的。
class Solution {// 优先使用梯子,梯子不够时选取差值最小的出堆改用砖头。(小根堆)public int furthestBuilding(int[] heights, int bricks, int ladders) {int n = heights.length, sum = 0;Queue<Integer> queue = new PriorityQueue<>();for(int i = 1; i < heights.length; i++) {int diff = heights[i] - heights[i - 1];if(diff > 0) {queue.offer(diff);if(queue.size() > ladders) {sum += queue.poll();}if(sum > bricks)return i - 1;}}return n - 1;}// 优先使用砖头,砖头不够时选取消耗最大的出堆改用梯子。(大根堆)public int furthestBuilding2(int[] heights, int bricks, int ladders) {int n=heights.length;PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->((int)o2-(int)o1));int suml=0,sumb=0;for(int i=1;i<n;i++){int diff=heights[i]-heights[i-1];if(diff>0){pq.add(diff);sumb+=diff;if(sumb>bricks){sumb-=pq.poll();suml++;}if(suml>ladders){return i-1;}}}return n-1;}
}作者:onion12138
链接:https://leetcode.cn/problems/furthest-building-you-can-reach/description/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2.3 LC871. 最低加油次数
2.3.1 解析
贪心 + 优先队列(堆)
我们可以模拟行进过程,使用 n 代表加油站总个数,idx 代表经过的加油站下标,使用 remain 代表当前有多少油(起始有 remain = startFuel),loc 代表走了多远,ans 代表答案(至少需要的加油次数)。只要 loc < target,代表还没到达(经过)目标位置,我们可以继续模拟行进过程。每次将 remain 累加到 loc 中,含义为使用完剩余的油量,可以去到的最远距离,同时将所在位置 stations[idx][0] <= loc 的加油站数量加入优先队列(大根堆,根据油量排倒序)中。再次检查是否满足 loc < target(下次循环),此时由于清空了剩余油量 remain,我们尝试从优先队列(大根堆)中取出过往油量最大的加油站并进行加油(同时对加油次数 ans 进行加一操作)。使用新的剩余油量 remain 重复上述过程,直到满足 loc >= target 或无油可加。容易证明该做法的正确性:同样是消耗一次加油次数,始终选择油量最大的加油站进行加油,可以确保不存在更优的结果。作者:宫水三叶
链接:https://leetcode.cn/problems/minimum-number-of-refueling-stops/solutions/1639184/by-ac_oier-q2mk/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution {public int minRefuelStops(int target, int startFuel, int[][] stations) {// 使用优先队列,承装所经过加油站的油PriorityQueue<Integer> q = new PriorityQueue<>((o1, o2) -> (o2 - o1));int ans = 0, len = stations.length;// 特判:if (len < 1) return startFuel < target ? -1 : 0;int fuel = startFuel;// 加进油箱的油(含使用过的)// 经过可以到达的所有的加油站,背上里面的油for (int i = 0; i < len; i ++) {while (fuel < stations[i][0]) {Integer add = q.poll();if (add == null) return -1;fuel += add;ans ++;}q.offer(stations[i][1]);}// 已经经过所有的加油站仍未到达,则用车油箱和后备箱里的所剩的fuel,以期到达while (fuel < target) {Integer add = q.poll();if (add == null) return -1;fuel += add;ans ++;}return ans;}/**题目思路:- 将路上的一个个加油站 视为 一桶桶的油,每次经过的时候,就把油带上放后备箱;- 当油不够的时候,取出后备箱所带的 最多的那桶油 加进油箱- 这样以来,如若油箱和后备箱的油加起来都不够,那么就到不了了*/// 方法二:需要后处理public int minRefuelStops2(int target, int startFuel, int[][] stations) {PriorityQueue<Integer> q = new PriorityQueue<>((a,b)->b-a);int re=startFuel;int ans=0;int n=stations.length;int pos=0;int idx=0;while(pos<target){if(re==0){if(!q.isEmpty()&&++ans>0){re=q.poll();}else{return -1;}}pos+=re;re=0;while(idx<n&&pos>=stations[idx][0]){q.add(stations[idx++][1]);}}return ans;}
}
2.4 LC630. 课程表 III (同2.2的解题思想非常相似)
class Solution {public int scheduleCourse(int[][] courses) {Arrays.sort(courses, (a,b)->a[1]-b[1]);PriorityQueue<Integer> q = new PriorityQueue<>((a,b)->b-a);int sum = 0;for (int[] c : courses) {int d = c[0], e = c[1];sum += d;q.add(d);if (sum > e) sum -= q.poll();}return q.size();}
}作者:宫水三叶
链接:https://leetcode.cn/problems/course-schedule-iii/solutions/1156693/gong-shui-san-xie-jing-dian-tan-xin-yun-ghii2/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
2.5 LC45. 跳跃游戏 II(左最优问题)
class Solution {public int jump(int[] nums) {int n=nums.length;int curf=0;int ans=0;int ml=0;// 遍历时稍带计算左侧局部最优for(int i=0;i<n;i++){if(curf>=n-1){return ans;}ml=Math.max(ml,i+nums[i]);if(i==curf){ans++;curf=ml;}}return ans;}}
2.6 股票问题:121. 买卖股票的最佳时机(虽然使用堆的方法不是最优解,但是方便和其他题目对比得出最优解)
// 使用堆维护最小值public int maxProfit(int[] prices) {int n=prices.length;//表示到第i天时,股票的历史最低点价格PriorityQueue<Integer>pq=new PriorityQueue<>((o1,o2)->(o1-o2));int max=0;for(int i=0;i<n;i++){pq.add(prices[i]);max=Math.max(max,prices[i]-pq.peek());}return max;}
3 “右最优” 类题目
3.1 LC670. 最大交换
搞懂两个问题,便可彻底理解本题的**(右最优)贪心核心**。
选择哪个数作为候选数与前面的数交换?——将最靠后的数定为候选数,若它之前出现了更大的数,则更新候选数为该数。
选择哪个数与候选数交换?——只有当候选数之前存在更小的数时,才需要交换这两数。若更靠前的位置出现小于候选数的数,则将它与候选数交换。
class Solution {public int maximumSwap(int num) {char[] cs = String.valueOf(num).toCharArray();int n = cs.length, max = n - 1;int[] maxIdx = new int[n]; // 记录每个数从当前位置往右的最大值索引for (int i = n - 1; i >= 0; i--) {if (cs[i] > cs[max]) max = i;maxIdx[i] = max;}for (int i = 0; i < n; i++) { // 从前往后找到第一个最大值不是自己本身的数if (cs[i] != cs[maxIdx[i]]) {char tmp = cs[i];cs[i] = cs[maxIdx[i]];cs[maxIdx[i]] = tmp;return Integer.parseInt(new String(cs));}}return num;}
}
4 同时涉及到左最优和右最优的题目
4.1 LC42 接雨水(需要两边同时进行预处理)
class Solution {public int trap(int[] height) {int n = height.length;if (n == 0) {return 0;}int[] leftMax = new int[n];leftMax[0] = height[0];for (int i = 1; i < n; ++i) {leftMax[i] = Math.max(leftMax[i - 1], height[i]);}int[] rightMax = new int[n];rightMax[n - 1] = height[n - 1];for (int i = n - 2; i >= 0; --i) {rightMax[i] = Math.max(rightMax[i + 1], height[i]);}int ans = 0;for (int i = 0; i < n; ++i) {ans += Math.min(leftMax[i], rightMax[i]) - height[i];}return ans;}
}作者:力扣官方题解
链接:https://leetcode.cn/problems/trapping-rain-water/solutions/692342/jie-yu-shui-by-leetcode-solution-tuvc/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

贪心算法的“左最优“与“右最优“及其对应的堆处理和预处理方法
1 答疑 1.1 什么是贪心算法的"左最优"与"右最优" "左最优"和"右最优"是贪心算法中的两种策略: 左最优 (Leftmost Greedy): 在每一步选择中,总是选择最左边(最早出现的)可行的选项。 右…...

【Docker】容器的相关命令
上一篇:创建,查看,进入容器 https://blog.csdn.net/m0_67930426/article/details/135430093?spm1001.2014.3001.5502 目录 1. 关闭容器 2.启动容器 3.删除容器 4.查看容器的信息 查看容器 1. 关闭容器 从图上来看,容器 aa…...

Android BUG 之 Error: Activity class {} does not exist
项目场景: 更换包名,运行报错 问题描述 原因分析: 在替换包名的时候要确认,配置文件跟build中的保持一致,在更换后还要将旧包的缓存数据清理掉 解决方案: 1 替换后删除 app 下的build 文件夹 2 Rebuild Pr…...
听劝,年度规划有它真的很必要!
2024年的时间进度条已走过一周,完成全年的1/52。 新年的flag悄然立下:愿逆风如解意,税后八个亿。 在不确定的世界中,发财暴富终归是确定的目标。 相比2023年的卷,年底的即兴生活正在悄悄上演,上一秒还在…...

leetcode滑动窗口问题总结 Python
目录 一、理论 二、例题 1. 最长无重复字符串 2. 长度最小的子数组 3. 字符串的排列 4. 最小覆盖子串 5. 滑动窗口最大值 一、理论 滑动窗口是一类比较重要的解题思路,一般来说我们面对的都是非定长窗口,所以一般需要定义两个指针 left 和 right&…...
秒变办公达人,只因用了这5款在线协同文档app!
在日常工作中,我们不可避免地需要处理各种文档,有时你可能会为如何高效地管理这些文档而感到烦恼,或是不知道如何挑选合适的在线文档工具? 不用担心!在这篇文章中,我们将介绍5个好用的在线文档工具App&…...

镜头选型和计算
3.5 补充知识 一、单像元分辨率(单像素精度) 单像素精度是表示视觉系统综合精度的指标,表示一个像元对应检测目标的实际物理尺寸,是客户重点关注的 视觉系统参数; 计算公式1:单像素精度视野范围FOV/相机分辨…...
2024--Django平台开发-Django知识点(四)
1.知识回顾 创建项目:新项目、别人项目、新版版、老版本 项目目录(v1.0版本) 路由系统 常见路由编写加粗样式 /index/ 函数 /index/<str:v1> 函数 re_path(ryy/(\d{4})-(\d{2})-(\d{2})/, views.yy), re_path(ryy/(?…...

可狱可囚的爬虫系列课程 09:通过 API 接口抓取数据
前面已经讲解过 Requests 结合 BeautifulSoup4 库抓取数据,这种方式在抓取数据时还是比较方便快捷的,但是这并不意味着所有的网站都适合这种方式,并且这也不是抓取数据的最快方式,今天我们来讲一种更快速的获取数据的方式…...

2. Spring Boot 自动配置 Mybatis 流程
1. Spring Boot 自动配置 Mybatis 自动配置过程中做了3个主要bean的创建及很重要的一些事情。 sqlSessionFactory、sqlSessionTemplate、MapperScannerConfigurer 等配置bean的创建。sqlSessionFactory:解析 xml配置文件,并将MappedStatement放入到Has…...
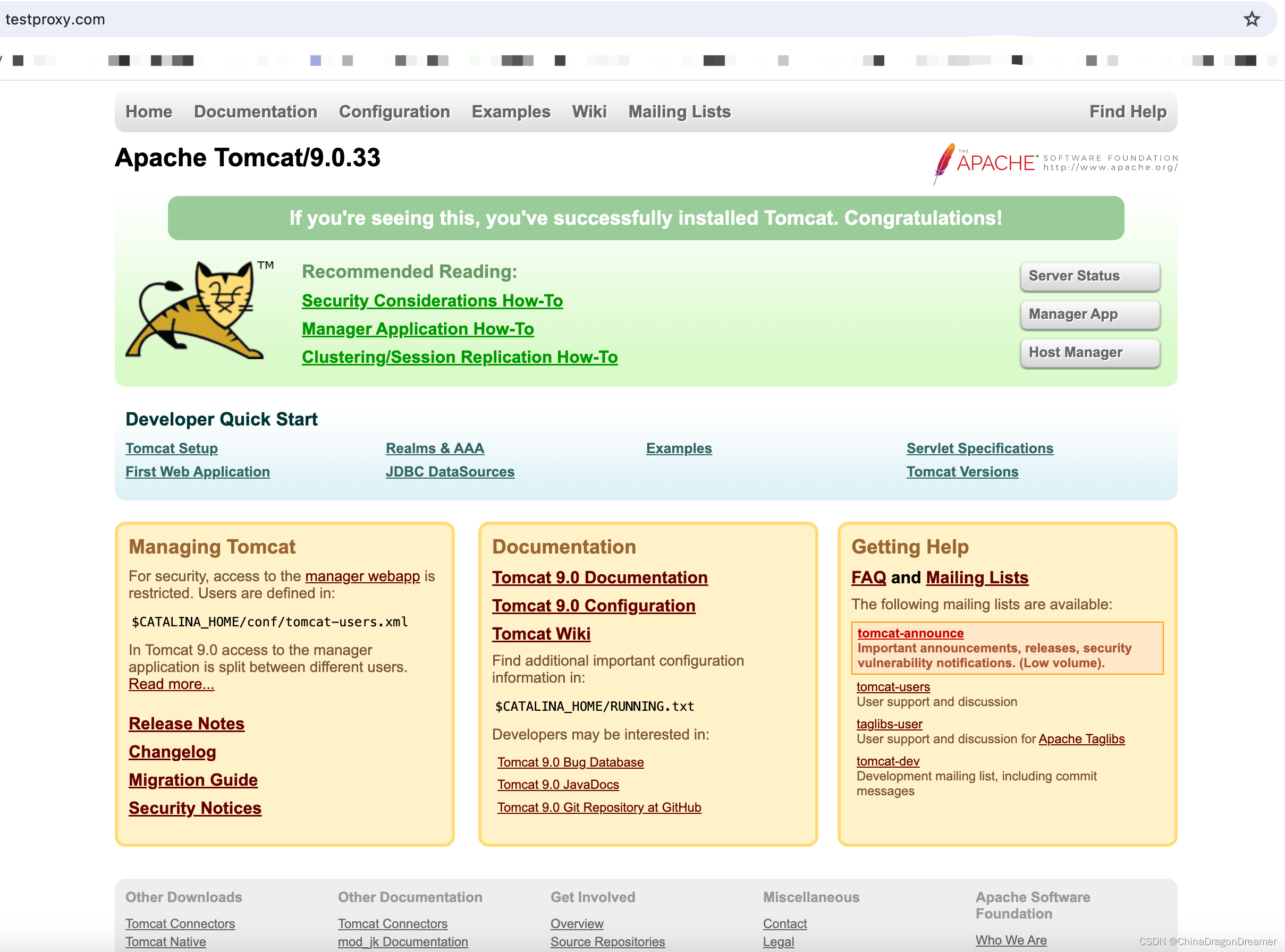
Nginx配置反向代理实例一
Mac 安装Nginx教程 提醒一下:下面实例讲解是在Mac系统演示的; 反向代理实例一实现的效果 在浏览器地址栏输入www.testproxy.com, 跳转到系统Tomcat主页面。 第一步:在系统的 hosts 文件进行ip和域名对应关系的配置。 Mac 系统修改Hosts文…...

训练自己的GPT2
训练自己的GPT2 1.预训练与微调2.准备工作2.在自己的数据上进行微调 1.预训练与微调 所谓的预训练,就是在海量的通用数据上训练大模型。比如,我把全世界所有的网页上的文本内容都整理出来,把全人类所有的书籍、论文都整理出来,然…...
etcd储存安装
目录 etcd介绍: etcd工作原理 选举 复制日志 安全性 etcd工作场景 服务发现 etcd基本术语 etcd安装(centos) 设置:etcd后台运行 etcd 是云原生架构中重要的基础组件,由 CNCF 孵化托管。etcd 在微服务和 Kubernates 集群中不仅可以作为服务注册…...

如何彻底卸载Microsoft Edge浏览器
一、引语 随着微软推出全新的Edge浏览器,许多用户可能想要尝试或完全切换到其他浏览器。在这篇文章中,我们将向您介绍如何彻底卸载Microsoft Edge浏览器,以确保您的系统干净整洁。 二、通过系统设置卸载 1、首先,右键单击桌面上…...
Transformers 2023年度回顾 :从BERT到GPT4
人工智能已成为近年来最受关注的话题之一,由于神经网络的发展,曾经被认为纯粹是科幻小说中的服务现在正在成为现实。从对话代理到媒体内容生成,人工智能正在改变我们与技术互动的方式。特别是机器学习 (ML) 模型在自然语言处理 (NLP) 领域取得…...

判断两个对象某些字段的值是否相同
1、借助mybatis plus的方法 import com.baomidou.mybatisplus.core.toolkit.LambdaUtils; import com.baomidou.mybatisplus.core.toolkit.support.SFunction; import com.baomidou.mybatisplus.core.toolkit.support.SerializedLambda; import lombok.SneakyThrows; import o…...

TYPE-C接口取电芯片介绍和应用场景
随着科技的发展,USB PDTYPE-C已经成为越来越多设备的充电接口。而在这一领域中,LDR6328Q PD取电芯片作为设备端协议IC芯片,扮演着至关重要的角色。本文将详细介绍LDR6328Q PD取电芯片的工作原理、应用场景以及选型要点。 一、工作原理 LDR63…...

基于TI TPSXX系列 Buck电路应用计算-外围器件详细计算过程
TPS54202 Buck电路应用计算 1、电气特性2、内部框图3、典型应用电路4、设计需求5、计算EN引脚电阻6、FB引脚电阻估算7、查看反馈电压电压基准8、输入电容计算10、FB引脚反馈电阻计算11、功率电感计算12、输出电容计算13、前馈电容计算15、Layout布局TPS54202-中文版 1、电气特…...
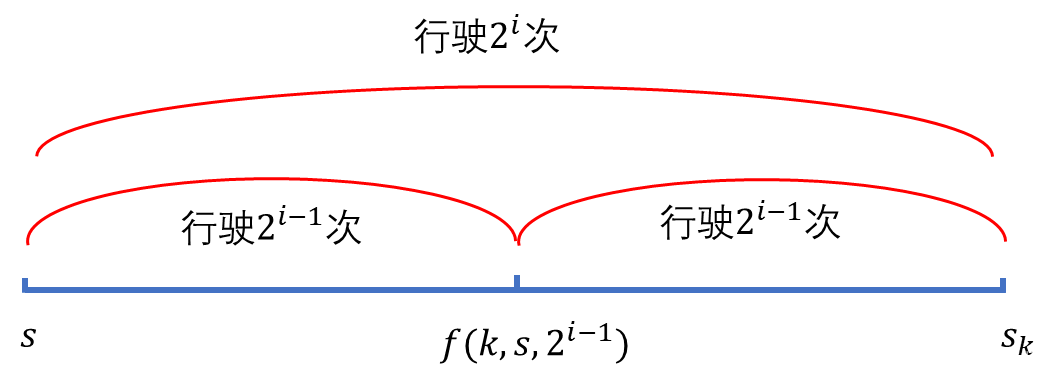
NOIP2012提高组day1-T3:开车旅行
题目链接 [NOIP2012 提高组] 开车旅行 题目描述 小 A \text{A} A 和小 B \text{B} B 决定利用假期外出旅行,他们将想去的城市从 1 1 1 到 n n n 编号,且编号较小的城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同…...

Golang Web框架性能对比
Golang Web框架性能对比 github star排名依次: Gin Beego Iris Echo Revel Buffalo 性能上gin、iris、echo网上是给的数据都是五星,beego三星,revel两星 beego是国产,有中文文档,文档齐全 根据star数,性能,易用程度…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
