介绍几种常见的质数筛选法
质数筛选法
- 1.暴力筛选法 :smirk:
- 2.普通优化 :rofl:
- 3.埃氏筛法:cold_sweat:
- 4.线性筛选法:scream:
质数:除了1和他本身没有其它因数的正整数就是质数。1不是质数,2是质数。
1.暴力筛选法 😏
- 原理
求x的质数,令y从2到 x \sqrt[]{x} x(向下取整,比如2.4=2)依次尝试 ,如果x%y=0,那么x不是质数。(2要单独讨论,否则按照这个逻辑2不是质数)。- 为什么取 x \sqrt[]{x} x?
答:如果取到 x \sqrt[]{x} x还没有找到x的约数,那么就可以断定x一定是质数!!。 x \sqrt[]{x} x* x \sqrt[]{x} x=x,这是一个特殊的位置。可以将这个等式抽象为a * b=x。a和b的关系是你消我涨,即a= x b {x \over b} bx。 x \sqrt[]{x} x是a=b的特殊情况,如果a小于等于 x \sqrt[]{x} x的数里没有x的约数,那么当a大于 x \sqrt[]{x} x的时候一样没有,因为a小于等于 x \sqrt[]{x} x的时候,b是大于等于 x \sqrt[]{x} x的。排除a不是x的约数的同时将b也排除了,因为约数是成对出现的。所以当a大于 x \sqrt[]{x} x的时候实际上在做重复的计算,相当于把a,b交换了一个位置,实际上当a取值小于等于 x \sqrt[]{x} x的时候已经把所有可能的约数排除了。 - 为什么 x \sqrt[]{x} x要向下取整而不是向上取整?
答:第一个问题解释了,约数是成对出现的,只需要枚举a从2到 x \sqrt[]{x} x即可,那么b= x a {x \over a} ax同时被考虑到了。如果 x \sqrt[]{x} x不是整数,那么就向下取整,去掉小数部分,这样可以保证a的枚举没有遗漏(a小于等于 x \sqrt[]{x} x)。如果向上取整,那么a的取值大于 x \sqrt[]{x} x,b小于 x \sqrt[]{x} x。这个组合实际上之前可能已经被排除了,所以重复计算了一对约数。可能会遗漏约数导致判断错误。 - 为什么2要单独考虑?
答:代码的逻辑是:从2到 x \sqrt[]{x} x依次找x的约数,但是2本身可以被2整除,这样就会误判2有约数,所以2要特判一下。
- 为什么取 x \sqrt[]{x} x?
- 代码
#include<iostream>
#include<cmath>
using namespace std;bool violence(int n) //violence 暴力
{if (n == 1)return false;if (n == 2)return true;for (int i = 2; i <= sqrt(n); i++) //sqrt函数向下取整的{if (n % i == 0)return false; //可以被i整除,不是质数}return true;
}int main()
{for (int i = 1; i <= 100; i++) // 找到1-100内的质数{if (violence(i))cout << i << " ";}return 0;
}
- 运行结果

2.普通优化 🤣
- 优化原理
- 先贴上代码好理解,否则讲半天不知道在说什么。(看完回到这里😊😊)
- 如果看懂了跳过,否则看下一行
- 唯一的难点🙁:为什么当 st[i] == false,则 i 一定是质数呢?
答:当遍历到 i 的时候,2~i-1的所有倍数都被标记成合数了,如果此时i没有被标记,说明i一定是质数。因为i的约数一定是在[2,i-1]的区间内的,而这个区间的所有数的倍数都不能构成i,说明这些数都不是i的约数,那么i就是质数。
int primes[N], cnt; // primes[]存储所有质数,cnt记录质数的下标
bool st[N]; // st[i]==true表示i不是质数void get_prime(int n) //挑选2到n中所有的质数
{for(int i = 2; i <= n; i ++){if(!st[i]) //当前的数是i,如果st[i]==false,那么说明i这个数一定是质数(理解不了先不解释,看后面的代码)primes[cnt ++] = i; //存储当前的质数for(int j = i + i; j <= n; j += i) //将i的所有倍数都标记为true,因为i的倍数一定不是质数。st[j] = true; }
}
3.埃氏筛法😰
-
数的公理( 两种形式)
( 1 ) 任意一个正整数(大于等于 2 ) = x 1 k 1 ∗ x 2 k 2 ∗ . . . . ∗ x n k n (1)任意一个正整数(大于等于2)=x_1^{k_1}*x_2^{k_2}*....*x_n^{k_n} (1)任意一个正整数(大于等于2)=x1k1∗x2k2∗....∗xnkn
( 2 ) 任意一个正整数(大于等于 2 ) = x 1 k 1 ∗ ( x 2 k 2 ∗ . . . . ∗ x n k n ) (2)任意一个正整数(大于等于2)=x_1^{k_1}*(x_2^{k_2}*....*x_n^{k_n}) (2)任意一个正整数(大于等于2)=x1k1∗(x2k2∗....∗xnkn)
其中 x n x_n xn都是质因数, k n k_n kn是大于等于0的正整数- 用人话说就是一个数分解开来,一定是若干个质数相乘,这些分开的数一定是质数😡,如果发现分解的数有合数,那么就没有分解彻底,再把合数分解成质数😡
-
优化原理
普通优化是将 i 之前的所有数的倍数都标记,以此判断i是不是合数。但是数的公理第2个形式说明了,一个数必然是由若干个质数的乘积构成的,那么就不需要取将i之前所有数的倍数标记,只需要将i之前的所有质数的乘积标记就可以了。
int primes[N], cnt; // primes[]存储所有质数,cnt记录质数的下标
bool st[N]; // st[i]==true表示i不是质数void get_primes(int n)//挑选2到n中所有的质数
{for (int i = 2; i <= n; i ++ ){if (st[i]) //如果st[i]==true,说明i不是质数continue; primes[cnt ++ ] = i;for (int j = i + i; j <= n; j += i) //只要把质数的倍数筛选掉就可以了。st[j] = true;}
}
4.线性筛选法😱
-
前集回顾
埃式筛选法有一个很明显的缺陷,即筛选(标记)合数的时候有大量重复的步骤。比如:
当 i = 3的时候,将6,9,,,51,,都标记了。当 i = 17 的时候,会标记,34,51,,,发现有重复的项51。 -
目的和公理
- 目的
让每个合数只会被筛选一次。 - 数学公理
每个数都有一个最小质因数,比如2的最小质因数是2,4的最小质因数是2,5的最小质因数是5,6的最小质因数是2,7的是7,8的是2,9的是3,10的是2,11的是11,12的是2…
- 目的
-
原理
任何数只有一个最小质因数,只要保证每个合数都是最小质因数筛选的,就可以保证不会重复筛选。(有点难以理解)
int primes[N], cnt; // primes[]存储所有质数,cnt记录质数的下标
bool st[N]; // st[i]==true表示i不是质数void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i; //合理性证明最底下for (int j = 0; primes[j] <= n/i; j ++ ){st[primes[j] * i] = true; //筛选的合数primes[j] * i的最小质因数一定是primes[j],就用primes[j]去筛选它if (i % primes[j] == 0) //为了避免重复筛选合数。//如果i % primes[j] == 0,则primes[j]是i的最小质因数,同时说明primes[j]是i*primes[j]的最小质因数(因为primes[j]是递增的),//如果继续循环,下一步就是st[primes[j+1]*i]=true,因为primes[j+1]>primes[j],primes[j+1]<=i,所以primes[j+1]*i的最小质因数仍然是primes[j],//但是根据原理,一个数需要被他的最小质因数筛选才不会重复,这里却用primes[j+1]筛选了primes[j+1]*i。重复筛选了。break;}}
}| i | 筛掉的数 |
|---|---|
| 2 | 4 |
| 3 | 6,9 |
| 4 | 8 |
| 5 | 10,15,25 |
| 6 | 12 |
| 7 | 14,21,35,49 |
| 8 | 16 |
| 9 | 19,27 |
| 10 | 20 |
| 11 | 22,33,55,77,121 |
Question区:
1.为什么st[i]=false可以表示是质数(明明下面的for循环和埃式筛选法不一样)
答:i= x 1 x_1 x1* x 2 x_2 x2, x 1 x_1 x1表示x的最小质因数, x 1 x_1 x1是[2,i-1]里面的一个质数, x 2 x_2 x2可以是质数也可以是合数。(1) x 2 x_2 x2是质数:我们从代码可以归纳出,当k(2~i-1)是质数的时候,它会筛掉所有的k * primes[j](j从0到cnt-1), 所以i会被[2,i-1]内的某一个质数筛掉。(2) x 2 x_2 x2是合数:我们从代码归纳出,当k是合数的时候,会筛选出[2,k的最小质因子] * primes[j], 而 x 1 x_1 x1是最小质因数,那么一定有一个k会筛选出 x 2 x_2 x2.
2.为什么要if (i % primes[j] == 0)break;
答:按照原理来的,每个数都要由他的最小质因数来更新,如果说这一步不退出而是继续循环,那么下一步i * primes[j+1]将被筛选掉,但是i * primes[j+1]的最小质因数是primes[j](因为i不变,上一步i%primes[j]==0且primes[j+1]>primes[j]),而现在i * primes[j+1]由primes[j+1]来筛选了,这样导致筛选过程提前了,后面又会筛选导致重复(当i变大的时候会再次筛选一次)。
线性筛选法还是很难理解的。本质在于:每个数只被筛选一次,且是被去最小质因数筛选的。
相关文章:

介绍几种常见的质数筛选法
质数筛选法 1.暴力筛选法 :smirk:2.普通优化 :rofl:3.埃氏筛法:cold_sweat:4.线性筛选法:scream: 质数:除了1和他本身没有其它因数的正整数就是质数。1不是质数,2是质数。 1.暴力筛选法 😏 原理 求x的质数,令y从2到 x \sqrt[]{x…...
)
Qt/QML编程学习之心得:Linux下读写GPIO(23)
在linux嵌入式系统中,经常需要一些底层操作,Linux就如window一样,也对底层BSP进行了封装,对device driver进行了封装,使用的话基本就是文件读写的方式来读取,所以也大大简化了上层应用对底层硬件的访问难度。 比如要对GPIO口进行访问,在Qt中有几种方法: 使用命令行方…...
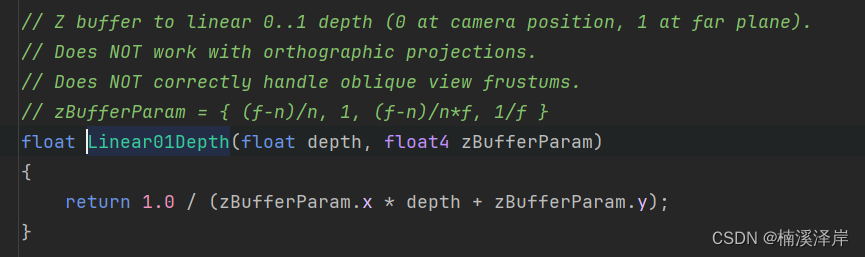
Unity中URP下深度图的线性转化
文章目录 前言一、_ZBufferParams参数有两组值二、LinearEyeDepth1、使用2、Unity源码推导:3、使用矩阵推导: 三、Linear01Depth1、使用2、Unity源码推导3、数学推导: 前言 在之前的文章中,我们实现了对深度图的使用。因为&#…...

Low Poly Cartoon House Interiors
400个独特的低多边形预制件的集合,可以轻松创建高质量的室内场景。所有模型都已准备好放入场景中,并使用一个纹理创建,以提高性能!包含演示场景! 模型分类: - 墙壁(79件) - 地板(28块) - 浴室(33个) - 厨房(36件) - 厨房道具(68件) - 房间道具(85件) - 灯具(…...
)
[算法与数据结构][c++]:左值、右值、左值引用、右值引用和std::move()
左值、右值、左值引用、右值引用和std::move 1. 什么是左值、右值2. 什么是左值引用、右值引用3. **右值引用和std::move的应用场景**3.1 实现移动语义3.2 **实例:vector::push_back使用std::move提高性能** **4. 完美转发 std::forward**5. Reference 写在前面&…...

【QT】day3
1.登陆界面 2.登陆失败 3.登陆成功弹窗 4.点击OK后跳转 #include "mainwindow.h" #include "ui_mainwindow.h"MainWindow::MainWindow(QWidget *parent): QMainWindow(parent), ui(new Ui::MainWindow) {ui->setupUi(this); }MainWindow::~MainWindow…...

c++ fork, execl 参数 logcat | grep
Linux进程编程(PS: exec族函数、system、popen函数)_linux popen函数会新建进程吗-CSDN博客 execvp函数详解_如何在C / C 中使用execvp()函数-CSDN博客 C语言的多进程fork()、函数exec*()、system()与popen()函数_c语言 多进程-CSDN博客 Linux---fork…...
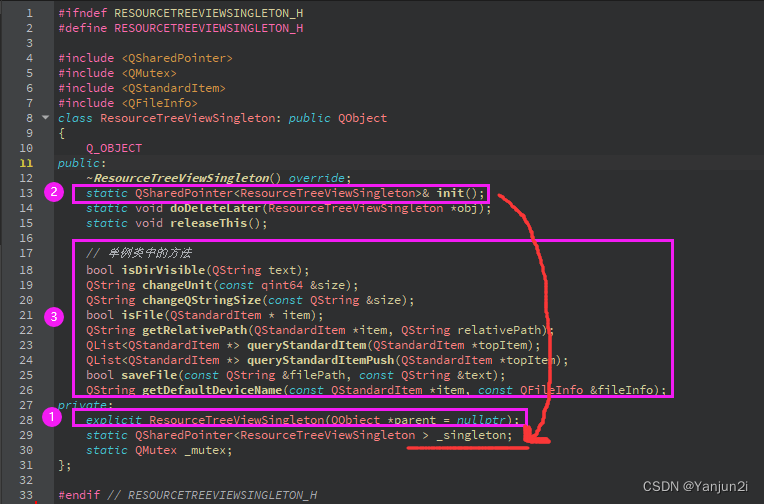
QT:单例
单例的定义 官方定义:单例是指确保一个类在任何情况下都绝对只有一个实例,并提供一个全局访问点。 单例的写法 抓住3点: 构造函数私有化(确保只有一个实例)提供一个可以获取构造实例的接口(提供唯一的实…...

IPv6路由协议---IPv6动态路由(OSPFv3-4)
OSPFv3的链路状态通告LSA类型 链路状态通告是OSPFv3进行路由计算的关键依据,链路状态通告包含链路状态类型、链路状态ID、通告路由器三元组唯一地标识了一个LSA。 OSPFv3的LSA头仍然保持20字节,但是内容变化了。在LSA头中,OSPFv2的LS age、Advertising Router、LS Sequence…...
移动通信原理与关键技术学习(4)
1.小尺度衰落 Small-Scale Fading 由于收到的信号是由通过不同的多径到达的信号的总和,接收信号的增强有一定的减小。 小尺度衰落的特点: 信号强度在很小的传播距离或时间间隔内的快速变化;不同多径信号多普勒频移引起的随机调频ÿ…...

第二百五十八回
文章目录 1. 概念介绍2. 思路与方法2.1 实现思路2.2 实现方法 3. 示例代码4. 内容总结 我们在上一章回中介绍了"模拟对话窗口的页面"相关的内容,本章回中将介绍如何创建一个可以输入内容的对话框.闲话休提,让我们一起Talk Flutter吧。 1. 概念…...

freesurfer-reconall后批量提取TIV(颅内总体积)
#提取TIV #singleline=$(grep Estimated Total Intracranial Volume /usr/local/freesurfer/subjects/bect-3d+bold-wangjingchen-4.9y-2/stats/aseg.sta...

【GO】如何用 Golang 的 os/exec 执行 pipe 替换文件
背景 主要记录一下怎么用 Golang 的 os/exec 去执行一个 cmd 的 pipeline,就是拿 cmdA 的输出作为 cmdB 的输入,这里记录了两种方法去替换文件里面的字符串。 pipe 那个逻辑在 demo1 里。 另外一种是直接读文件做替换,一不小心两个都放进来了…...
基于Spring-boot-websocket的聊天应用开发总结
目录 1.概述 1.1 Websocket 1.2 STOMP 1.3 源码 2.Springboot集成WS 2.1 添加依赖 2.2 ws配置 2.2.1 WebSocketMessageBrokerConfigurer 2.2.2 ChatController 2.2.3 ChatInRoomController 2.2.4 ChatToUserController 2.3 前端聊天配置 2.3.1 index.html和main.j…...

2023年度总结 - 职业生涯第一个十年
2023年只剩下最后一周,又到了一年一度该做年末总结的时候了。 回想起去年,还有人专门建立了一个关于年度总结文章汇总的仓库。读了很多篇别人写的,给了我很多的触动和感想。这里的每篇文章都是关于某个人这一整年的生活和工作的轨迹啊。即使你…...
setup 语法糖
只有vue3.2以上版本可以使用 优点: 更少的样板内容,更简洁的代码 能够使用纯 Typescript 声明props 和抛出事件 更好的运行时性能 更好的IDE类型推断性能 在sciprt标识上加上setup 顶层绑定都可以使用 不需要return ,可以直接使用 使用组件…...
Javaweb之Mybatis的基础操作的详细解析
1. Mybatis基础操作 学习完mybatis入门后,我们继续学习mybatis基础操作。 1.1 需求 需求说明 通过分析以上的页面原型和需求,我们确定了功能列表: 查询 根据主键ID查询 条件查询 新增 更新 删除 根据主键ID删除 根据主键ID批量删除 …...

知名开发者社区Stack Overflow发布《2023 年开发者调查报告》
Stack Overflow成立于2008年,最知名的是它的公共问答平台,每月有超过 1 亿人访问该平台来提问、学习和分享技术知识。是世界上最受欢迎的开发者社区之一。每年都会发布一份关于开发者的调查报告,来了解不断变化的开发人员现状、正在兴起或衰落…...

vue element plus Form 表单
表单包含 输入框, 单选框, 下拉选择, 多选框 等用户输入的组件。 使用表单,您可以收集、验证和提交数据。 TIP Form 组件已经从 2. x 的 Float 布局升级为 Flex 布局。 典型表单# 最基础的表单包括各种输入表单项,比如input、select、radio、checkbo…...

zmq_connect和zmq_poll
文章内容: 介绍函数zmq_connect和zmq_poll的使用 zmq_connect zmq_connect函数是ZeroMQ库中的一个函数,用于在C语言中创建一个与指定地址的ZeroMQ套接字的连接。该函数的原型如下: int zmq_connect(void *socket, const char *endpoint);其…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
