自然语言处理5——发掘隐藏规律 - Python中的关联规则挖掘
目录
- 写在开头
- 1. 了解关联规则挖掘的概念和实际应用
- 1.1 关联规则挖掘在市场分析和购物篮分析中的应用
- 1.2 关联规则的定义和基本原理
- 1.3 应用场景
- 2. 使用Apriori算法和FP-growth算法进行关联规则挖掘
- 2.1 Apriori算法的工作原理和实现步骤
- 2.2 FP-growth算法的优势和使用方法
- 2.3 Apriori算法 vs FP-growth算法
- 3. 结果解读和关联规则可视化
- 3.1 如何解读挖掘出的关联规则
- 3.2 利用可视化工具展示关联规则的分布
- 写在最后
写在开头
在当今大数据时代,数据分析和挖掘技术成为解决实际问题和优化业务流程的重要工具。其中,关联规则挖掘作为一种强大的数据挖掘技术,在市场分析和购物篮分析中发挥着重要作用。本文将带领你深入了解关联规则挖掘的概念、实际应用,以及如何使用Python中的Apriori算法和FP-growth算法进行关联规则挖掘。最后,我们将探讨如何解读挖掘结果并通过可视化工具展示关联规则的分布。
1. 了解关联规则挖掘的概念和实际应用
1.1 关联规则挖掘在市场分析和购物篮分析中的应用
在市场分析中,关联规则挖掘是一种强大的工具,特别是在购物篮分析方面。通过分析顾客购物篮中的商品组合,企业可以发现不同商品之间的关联性,从而制定更精准的市场策略。例如,超市可能发现了牛奶和面包之间的强关联关系,于是将它们摆放在相邻货架上,提高了购买这两种商品的可能性,增加了销售额。
1.2 关联规则的定义和基本原理
定义: 关联规则是指在数据集中不同项之间存在的相关性或联合出现的模式。这些规则通常采用“X ⇒ Y”的形式,其中X和Y是数据集中的项,意味着当X出现时,可能会伴随着Y的出现。
基本原理: 关联规则挖掘的过程始于寻找频繁项集。频繁项集是在数据集中频繁出现的项的组合。常用的方法包括扫描数据集以计算每个项集的支持度(Support)。支持度表示项集出现的频率,高支持度的项集即为频繁项集。
生成关联规则: 基于频繁项集,可以计算置信度(Confidence)来生成关联规则。置信度是规则的可信度,例如,如果A出现,则B也出现的概率。高置信度的规则更可靠,通常作为有用的关联规则进行筛选。
购物篮分析的实现,是基于条件概率,也就是贝叶斯公式。在实际应用时,主要会牵扯到3个指标:置信度、支持度和提升度。
将信息展示如下,N代表数量:
| 指标名称 | 指标说明 | 计算公式 | 举例 |
|---|---|---|---|
| 产品A的订单数 | 有购买过产品A的订单数量 | N(A) | 400 |
| 产品B的订单数 | 有购买过产品B的订单数量 | N(B) | 300 |
| 同时购买产品A和B的订单数 | 同时购买过产品A和B的订单数量 | N(A∩B) | 200 |
| 总订单数 | 所有订单数量 | N(I) | 1000 |
| 支持度 | 支持的程度,一般用百分比表示。本例中,A和B的支持度,即A和B同时出现的频率,如果A和B一起出现的频率非常小,那么就说明了A和B之间的联系并不大 | A和B的支持度=N(A∩B)/ N(I) | 200/1000=20% |
| 置信度 | 揭示了A出现时,B是否一定会出现,如果出现则其大概有多大的可能出现 | P(B|A)=P(A∩B) /P(A)=[N(A∩B)/N(I)]/[N(A)/N(I)]=N(A∩B)/N(A) | 200/400=50% |
| 提升度 | 提升度反映了关联规则中的A与B的相关性,提升度>1且越高表明正相关性越高,提升度<1且越低表明负相关性越高,提升度=1表明没有相关性,即相互独立。 | P(A→B)=P(B|A)/P(B) =[N(A∩B)/N(I)]/[N(A)/N(I)]/[N(B)/N(I)]=N(A∩B)*N(I)/N(A)/N(B) | 法1:0.5/(300/1000)=0.5/0.3≈1.67 法2:150*1000/400/300≈1.67 |
1.3 应用场景
市场分析和购物篮分析
在零售业中,关联规则被广泛用于购物篮分析。超市利用这些规则发现消费者购买商品之间的关联关系,从而优化产品摆放、促销策略和交叉销售。例如,发现经常一起购买的商品,如牛奶和谷物,超市可以将它们放在相邻货架上,提高销售量。
医疗保健
在医疗领域,关联规则用于分析疾病和治疗方法之间的关系。医疗专家可以利用关联规则来发现特定病症与药物的关联性,指导临床决策,并提供更个性化的治疗方案。
网络安全
在网络安全中,关联规则挖掘可用于检测异常行为或入侵。通过分析网络流量数据,系统可以发现不同事件之间的关联模式,识别潜在的威胁或攻击,从而及时采取防御措施。
2. 使用Apriori算法和FP-growth算法进行关联规则挖掘
2.1 Apriori算法的工作原理和实现步骤
Apriori算法是一种经典的关联规则挖掘算法,它基于“先验原理”,即如果一个项集是频繁的,那么它的所有子集也是频繁的。这一原理减少了搜索空间,提高了算法效率。实现Apriori算法的步骤包括扫描数据集、生成候选项集、计算支持度、筛选频繁项集等。之前我在文章里有过详细的介绍,如果感兴趣,欢迎访问Python实现产品关联性分析apriori算法 ,此处仅作简单展示:
import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori, association_rules# 构建超市购物篮数据
data = [['面包', '牛奶', '啤酒'],['面包', '牛奶', '尿布', '蛋糕'],['牛奶', '尿布', '啤酒', '可乐'],['面包', '牛奶', '尿布', '啤酒'],['面包', '牛奶', 相关文章:

自然语言处理5——发掘隐藏规律 - Python中的关联规则挖掘
目录 写在开头1. 了解关联规则挖掘的概念和实际应用1.1 关联规则挖掘在市场分析和购物篮分析中的应用1.2 关联规则的定义和基本原理1.3 应用场景2. 使用Apriori算法和FP-growth算法进行关联规则挖掘2.1 Apriori算法的工作原理和实现步骤2.2 FP-growth算法的优势和使用方法2.3 A…...

【记录】重装系统后的软件安装
考完研重装了系统,安装软件乱七八糟,用到什么装什么。在这里记录一套标准操作,备用。一个个装还是很麻烦,我为什么不直接写个脚本直接下载安装包呢?奥,原来是我太菜了还不会写脚本啊!先记着吧&a…...
- ACodec(七))
Android 13 - Media框架(31)- ACodec(七)
之前的章节中我们解了 input buffer 是如何传递给 OMX 的,以及Output buffer 是如何分配并且注册给 OMX 的。这一节我们就来看ACodec是如何处理OMX的Callback的。 1、OMXNodeInstance Callback 这一节我们只大致记录Callback是如何传递给ACodec的。在之前的学习中我…...

快速了解VR全景拍摄技术运用在旅游景区的优势
豆腐脑加了糖、烤红薯加了勺,就连索菲亚大教堂前都有了“人造月亮”,在这个冬季,“尔滨”把各地游客宠上了天。面对更多的游客无法实地游玩,哈尔滨冰雪世界再添新玩法,借助VR全景拍摄技术对冬季经典冰雪体验项目进行全…...

分布形态的度量_峰度系数的探讨
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还应掌握数据分布的形态。 描述数据分布形态的度量有偏度系数和峰度系数, 其中偏度系数描述数据的对称性,峰度系数描述与正态分布的偏离程度。 峰度系数反映分布峰的尖峭程度的重要指标. 当…...
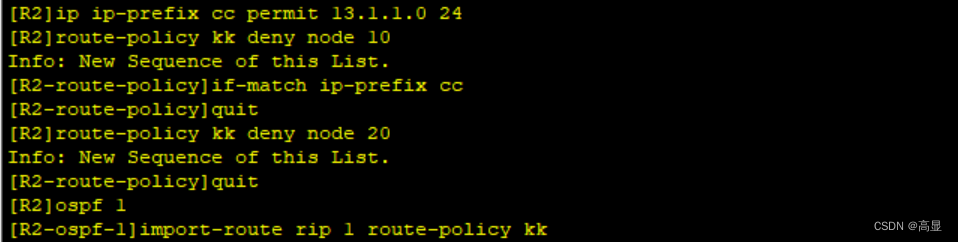
HCIP 重发布
拓扑图&IP划分如下: 第一步,配置接口IP&环回地址 以R1为例,R2~R4同理 interface GigabitEthernet 0/0/0 ip address 12.1.1.1 24 interface GigabitEthernet 0/0/1 ip address 13.1.1.1 24 interface LoopBack 0 ip address 1.1.1.…...

FX图中的节点代表什么操作
在 FX 图中,每个节点代表一个操作。这些操作可以是函数调用、方法调用、模块实例调用,也可以是 torch.nn.Module 实例的调用。每个节点都对应一个调用站点,如运算符、方法和模块。 一.节点操作 下面是一些节点可能代表的操作: 1…...

【Java 设计模式】创建型之单例模式
文章目录 1. 定义2. 应用场景3. 代码实现1)懒汉式2)饿汉式 4. 应用示例结语 在软件开发中,单例模式是一种常见的设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式在需要控制某些资源,如数…...
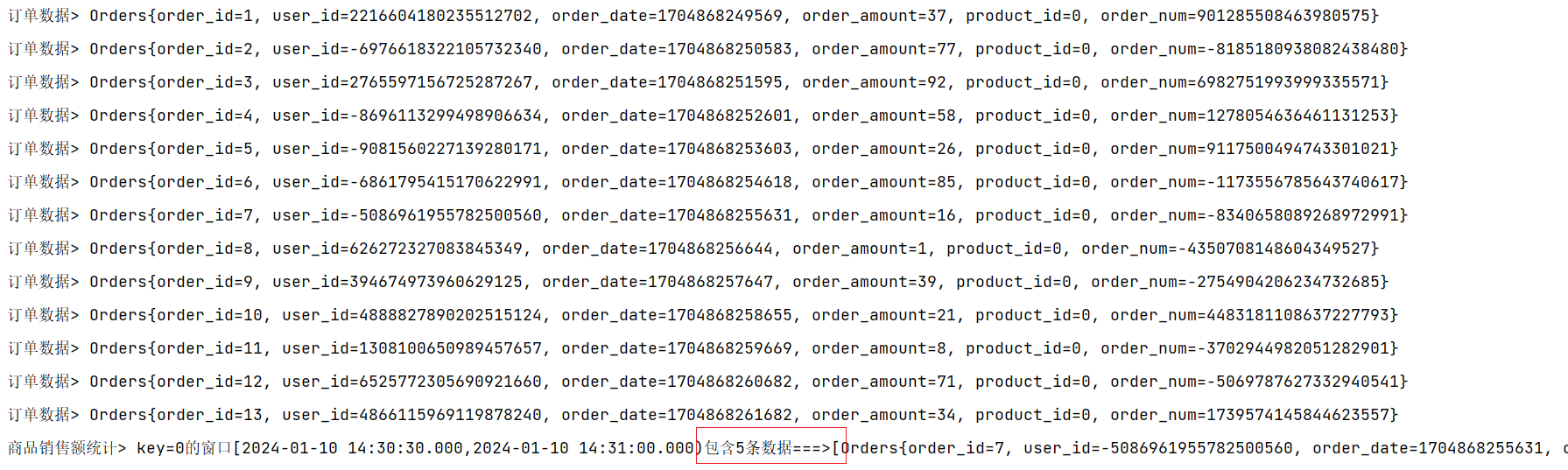
FlinkAPI开发之窗口(Window)
案例用到的测试数据请参考文章: Flink自定义Source模拟数据流 原文链接:https://blog.csdn.net/m0_52606060/article/details/135436048 窗口的概念 Flink是一种流式计算引擎,主要是来处理无界数据流的,数据源源不断、无穷无尽。…...
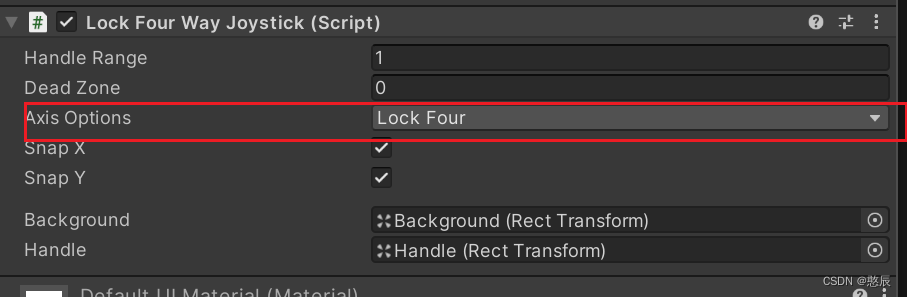
【Unity】Joystick Pack摇杆插件实现锁四向操作
Joystick Pack 简介:一款Unity摇杆插件,非常轻量化 摇杆移动类型:圆形、横向、竖向 摇杆类型: Joystick描述Fixed固定位置Floating浮动操纵杆从用户触碰的地方开始,一直固定到触碰被释放。Dynamic动态操纵…...

29 旋转工具箱
效果演示 实现了一个菜单按钮的动画效果,当鼠标悬停在菜单按钮上时,菜单按钮会旋转315度,菜单按钮旋转的同时,菜单按钮旋转的8个小圆圈也会依次旋转360度,并且每个小圆圈的旋转方向和菜单按钮的旋转方向相反࿰…...
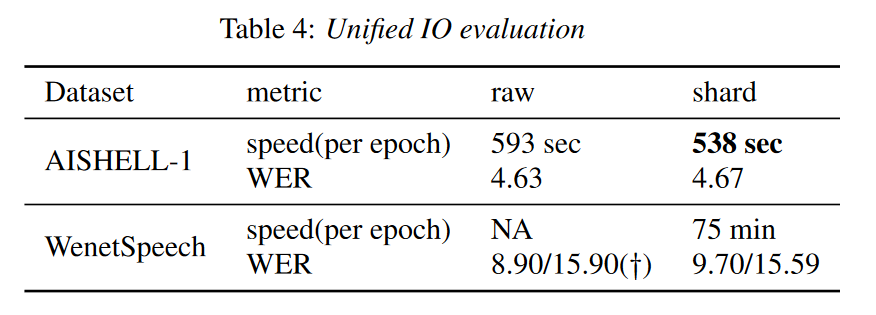
WeNet2.0:提高端到端ASR的生产力
摘要 最近,我们提供了 WeNet [1],这是一个面向生产(工业生产环境需求)的端到端语音识别工具包,在单个模型中,它引入了统一的两次two-pass (U2) 框架和内置运行时(built-in runtime)…...
)
第九部分 使用函数 (四)
目录 一、foreach 函数 二、if 函数 三、call 函数 一、foreach 函数 foreach 函数和别的函数非常的不一样。因为这个函数是用来做循环用的,Makefile 中的 foreach 函数几乎是仿照于 Unix 标准 Shell(/bin/sh)中的 for 语句,或…...
一文读懂「Prompt Engineering」提示词工程
在了解提示过程之前,先了解一下什么是提示prompt,见最后附录部分 一、什么是Prompt Engingering? 提示工程(Prompt Engingering),也被称为上下文提示(In-Context Prompting)&#x…...

微信小程序(一)简单的结构及样式演示
注释很详细,直接上代码 涉及内容: view和text标签的使用类的使用flex布局水平方向上均匀分布子元素垂直居中对齐子元素字体大小文字颜色底部边框的宽和颜色 源码: index.wxml <view class"navs"><text class"active…...

【设计模式】外观模式
前言 1. 单例模式(Singleton Pattern):保证一个类只有一个实例,并提供一个全局的访问点。 2. 工厂模式(Factory Pattern):定义一个创建对象的接口,但由子类决定要实例化的类是哪一…...
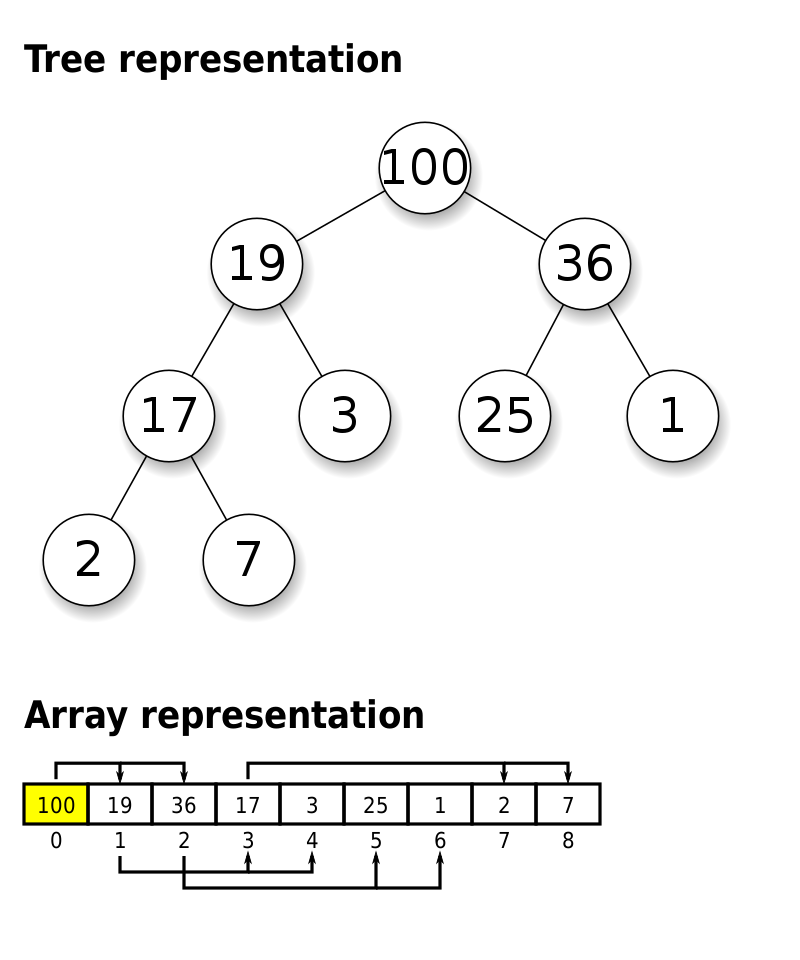
优先级队列(Priority Queue)
文章目录 优先级队列(Priority Queue)实现方式基于数组实现基于堆实现方法实现offer(E value)poll()peek()isEmpty()isFull() 优先级队列的实现细节 优先级队列(Priority Queue) 优先级队列是一种特殊的队列,其中的元素…...
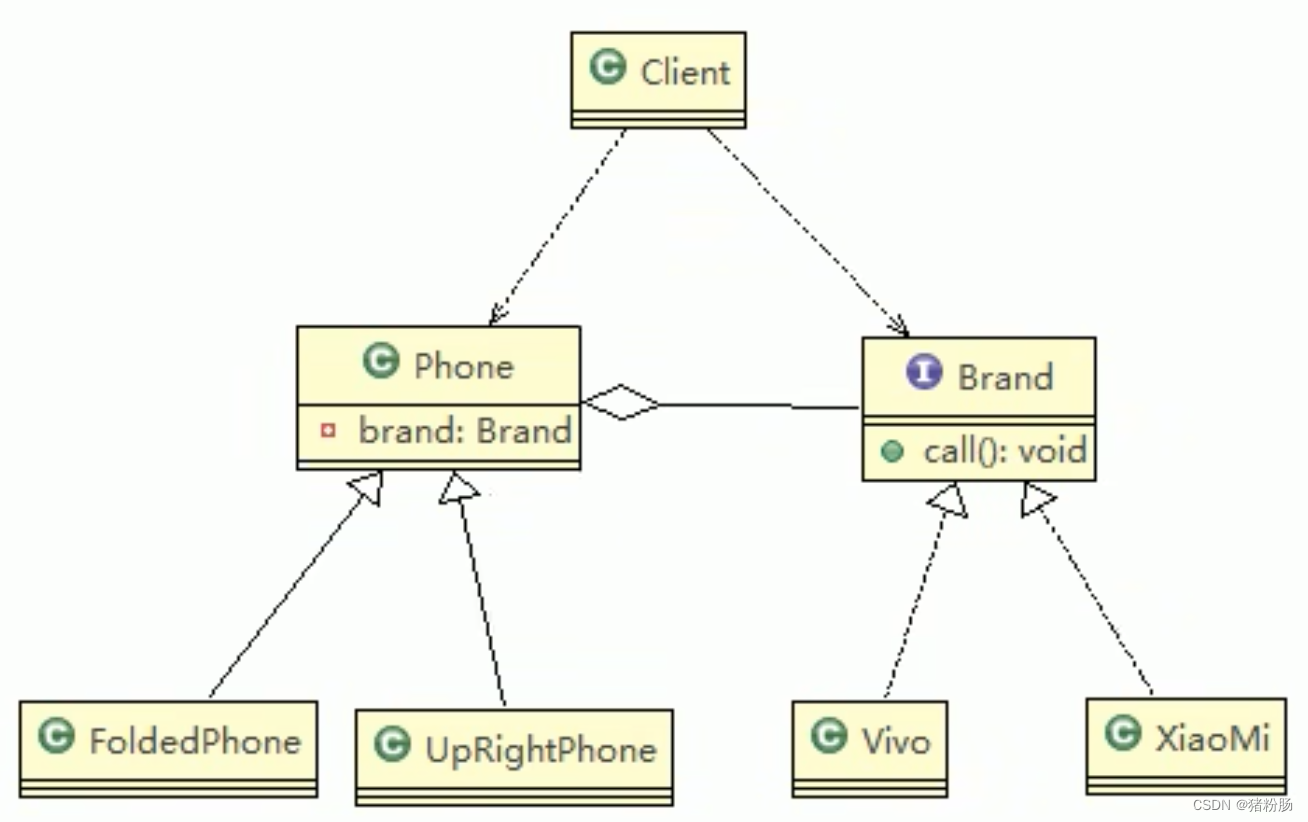
12-桥接模式(Bridge)
意图 将抽象部分与它的实现部分分离,使他们可以独立地变化 个人理解 一句话概括就是只要是在抽象类中聚合了某个接口或者抽象类,就是使用了桥接模式。 抽象类A中聚合了抽象类B(或者接口B),A的子类的方法中在相同的场…...

Zookeeper+Kafka概述
一 Zookeeper 1.1 Zookeeper定义 Zookeeper是一个开源的、分布式的,为分布式框架提供协调服务的Apache项目。 1.2 Zookeeper特点 Zookeeper:一个领导者(leader),多个跟随者(Follower)组成的…...
架构师 - 架构师是做什么的 - 学习总结
架构师核心定义 架构师是什么 架构师是业务和技术之间的桥梁 架构师的核心职责是消除不确定性、和降低复杂性 架构设计环 架构师的三个核心能力 架构师的三个关键思维 架构师主要职责 架构设计 Vs 方案设计 架构设计前期 主要任务 澄清不确定性 明确利益干系人的诉求消除冲…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
