时间复杂度的计算
个人主页:平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶(C实现)】
文章目录
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
时间复杂度(就是一个函数)的计算,在算法中的基本操作的执行次数。就是算法的时间复杂度。
1
void Func1(int N)
{int count = 0;for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){count++;}}for (int k = 0; k < 2 * N; k++){count++;}int M = 10;while (M--){count++;}printf("%d\n", count);
}
Func1执行的基本操作次数:F(N)=N^2+2*N+10。Func1的时间复杂度就是O(N^2)。
2
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; k++){count++;}int M = 10;while (M--){count++;}printf("%d\n", count);
}
Func2的时间复杂度是O(N)。
3
void Func3(int N,int M)
{int count = 0;for (int k = 0; k < M; k++){count++;}for (int k = 0; k < N; k++){count++;}printf("%d\n", count);
}
Func3的时间复杂度是:O(M+N)。
4
void Func4(int N)
{int count = 0;for (int k = 0; k < 100; k++){count++;}printf("%d\n", count);
}
对于这种运行次数可以确定为常数次的时间复杂度就是O(1)。
5
const char* strchr(const char* str, int character)
{while (*str){if (*str == character){return str;}str++;}
}
最好情况:1次找到。
最坏情况:N次找到。
平均情况:N/2次找到。
由于在实际算法种关注的是算法最坏情况的运行情况,所以说数组中搜索数据时间复杂度为O(N)。
6
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] > x){end = mid - 1;}else if (a[mid] < x){begin = mid + 1;}else{return mid;}}return -1;
}
二分查找就是用来查找你要查找的数据的,如果找到了,就返回所要查找数据的下标。
先来看一下最好情况:O(1),即查找一次就找到了。
看一下最坏情况:log以2为底,N的对数。

最好情况是1次很好理解,即把数据折半一次就找到了。
我们来看一下最坏的情况:我们首先要知道,查找一次,数据就要折半一次,查找一次,数据就要折半一次;所以当你一直查找,即一直折半直到折半到只有一个数据的时候,此时要么找到了,要么就没找到(没找到就是这些数据中根本就没有你所要查找的数据)。
比如:假设N是数组中元素的个数,x表示最坏情况的查找次数。查找一次就折半一次,即N/2,查找第二次:N/2/2;查找第三次:N/2/2/2,所以你要查找几次就需要除以几个2,直到最后查找到最后数组中只剩下一个元素的时候,即N/2/2/2/2……/2(除以x个2)=1;
把该式子整理一下就变成了这样:2^x=N,x=log以2为底N的对数。即:

7
//计算阶乘递归Fac的时间复杂度
long long Fac(size_t N)
{if (N == 0){return 1;//0!=1}else{return Fac(N - 1) * N;}
}
时间复杂度是O(N),准确来说是O(N+1),只不过那个1忽略不计了。

8
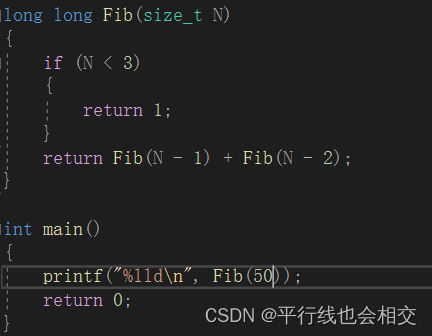
//计算斐波那契数列Fib的时间复杂度
long long Fib(size_t N)
{if (N < 3){return 1;}return Fib(N - 1) + Fib(N - 2);
}

但是这个算法很慢,当N是50的时候就要运行很长时间才行。

9
void BubbleSort(int* a, int n)
{assert(a);int i = 0;for (i = 0; i < n-1; i++){int j = 0;int count = 0;for (j = 0; j < n - 1 - i; j++){if (a[j] > a[j + 1]){int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;count = 1;}}if (count == 0){break;}}
}
最好情况就是冒泡排序的第一趟就好了即O(N)。
最坏情况:O(N^2)。

好了,以上就是一些时间复杂度的一些计算,就到这里吧各位。
再见啦!!!

相关文章:

时间复杂度的计算
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【数据结构初阶(C实现)】 文章目录123456789时间复杂度(就是一个函数)的计算,…...
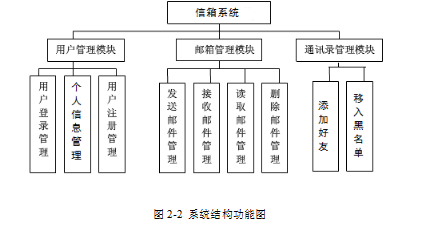
站内信箱系统的设计与实现
技术:Java、JSP等摘要:在经济全球化和信息技术成为发展迅速的今时今日,人们通过电子邮件收发进行信息传递已经成为主流。随着互联网和网络办公的发展,电子邮件正在被广泛应用在人们的日常生活中。跟据调查研究统计,在全…...

systemV共享内存
systemV共享内存 共享内存区是最快的IPC形式。共享内存的大小一般是4KB的整数倍,因为系统分配共享内存是以4KB为单位的(Page)!4KB也是划分内存块的基本单位。 之前学的管道,是通过文件系统来实现让不同的进程看到同一…...

Python基础之if逻辑判断
在学习if语句之前,我们先学习一种数据类型,布尔类型(bool),在if语句中,我们需要通过判断条件是否为真或者假,才进入下面的语句块执行。 一、布尔类型(bool) 布尔类型&a…...
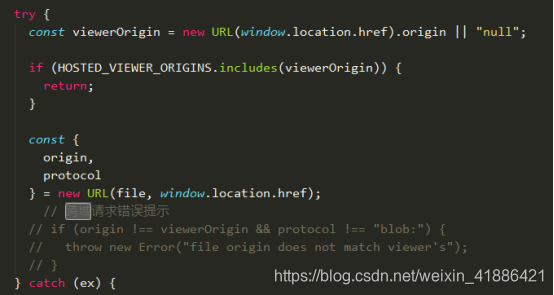
实现pdf文件预览
前言 工作上接到的一个任务,实现pdf的在线预览,其实uniapp中已经有对应的api:uni.openDocument(OBJECT)(新开页面打开文档,支持格式:doc, xls, ppt, pdf, docx, xlsx, pptx。)**实现了相关功能…...

【java】alibaba Fastjson --全解史上最快的JSON解析库
文章目录前序Fastjson 简介Fastjson 的优点速度快使用广泛测试完备使用简单功能完备下载和使用将 Java 对象转换为 JSON 格式JSONField创建 JSON 对象JSON 字符串转换为 Java 对象使用 ContextValueFilter 配置 JSON 转换使用 NameFilter 和 SerializeConfigFastjson 处理日期F…...
(十道编程题))
绝对零基础的C语言科班作业(期末模拟考试)(十道编程题)
编程题(共10题; 共100.0分)(给猛男妙妙屋更一篇模拟考试)模拟1(输出m到n的素数)从键盘输入两个整数[m,n], 输出m和n之间的所有素数。 输入样例:3,20输出样例:…...

按位与为零的三元组[掩码+异或的作用]
掩码异或的作用前言一、按位与为零的三元组二、统计分组1、map统计分组2、异或掩码总结参考资料前言 当a b 0时,我们能够很清楚的知道b是个什么值,b 0 - a -a,如果当a & b 0时,我们能够很清楚的知道b是什么值吗…...

C++基础篇(一)-- 简单入门
C 语言是在优化 C 语言的基础上为支持面向对象的程序设计而研制的一个通用目的的程序设计语言。在后来的持续研究中,C 增加了许多新概念,例如虚函数、重载、继承、标准模板库、异常处理、命名空间等。 C 语言的特点主要表现在两个方面:全面兼…...
前端整理 —— javascript 2
1. generator(生成器) 详细介绍 generator 介绍 generator 是 ES6 提供的一种异步编程解决方案,在语法上,可以把它理解为一个状态机,内部封装了多种状态。执行generator,会生成返回一个遍历器对象。返回的…...
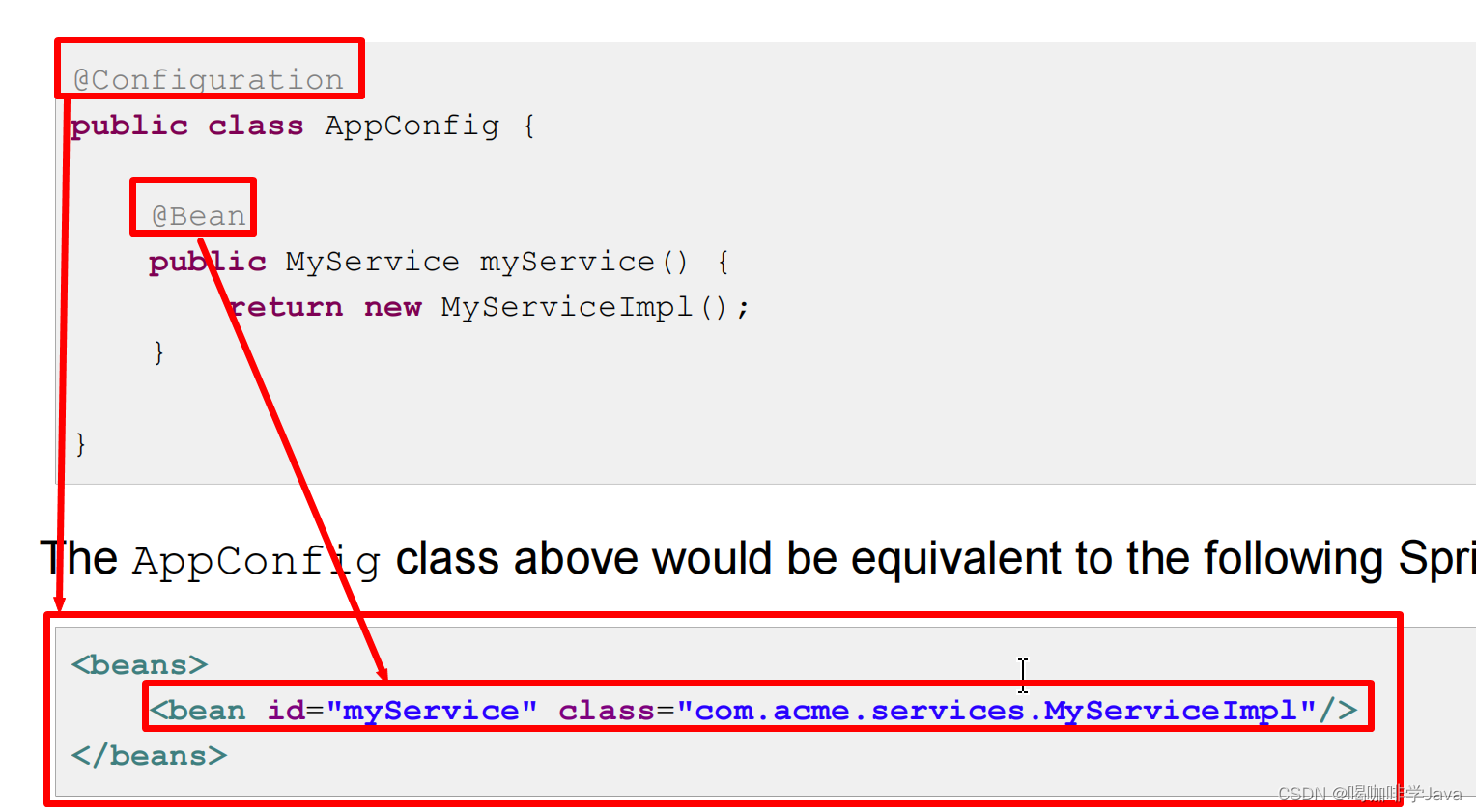
Spring-注解注入
一、回顾XML注解 bean 配置 创建 bean public class Student { } 配置 xml bean <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/2001/XMLSche…...
)
华为校招机试 - 攻城战(Java JS Python)
目录 题目描述 输入描述 输出描述 用例 题目解析 JavaScript算法源码 Java算法源码...

Docker入门
Docker一、何为DockerDocker是一个开源的应用容器引擎,基于GO语言并遵循从Apache2.0协议开源。Docker可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后在发布到任何流行的Linux机器上,也可以实现虚拟化。容器是完全使…...

时间序列分析 | CNN-LSTM卷积长短期记忆神经网络时间序列预测(Matlab完整程序)
时间序列分析 | CNN-LSTM卷积长短期记忆神经网络时间序列预测(Matlab完整程序) 目录 时间序列分析 | CNN-LSTM卷积长短期记忆神经网络时间序列预测(Matlab完整程序)预测结果模型输出基本介绍完整程序参考资料预测结果 模型输出 layers = 具有以下层的 151 Layer 数组:...
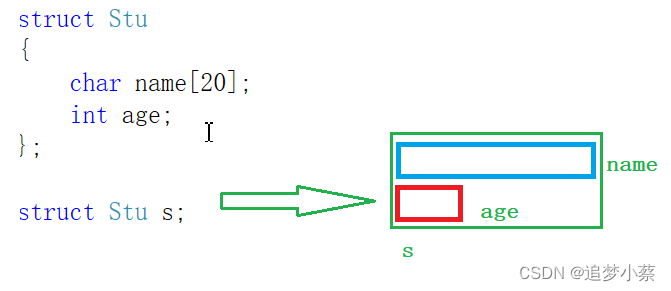
【蒸滴C】C语言结构体入门?看这一篇就够了
目录 一、结构体的定义 二、结构的声明 例子 三、 结构成员的类型 结构体变量的定义和初始化 1.声明类型的同时定义变量p1 2.直接定义结构体变量p2 3.初始化:定义变量的同时赋初值。 4.结构体变量的定义放在结构体的声明之后 5.结构体嵌套初始化 6.结构体…...

第十三届蓝桥杯
这里写目录标题一、刷题统计(ceil函数返回的是等值于某最小整数的浮点值,不强制转换回int就wa,没错就连和int整数相加都wa二、修剪灌木(主要应看清楚会调转方向三、统计子矩阵(前缀和滑动窗口⭐)四、[积木画…...

消息队列mq
应用场景: 1、解耦 2、削峰填谷 3、异步处理 4、消息通讯 工作模式: 一个消息只能被消费一次(订阅模式除外),消费者接受到消息会回调业务逻辑,消费逻辑写在回调函数里面。 1、简单模式:一个生产…...
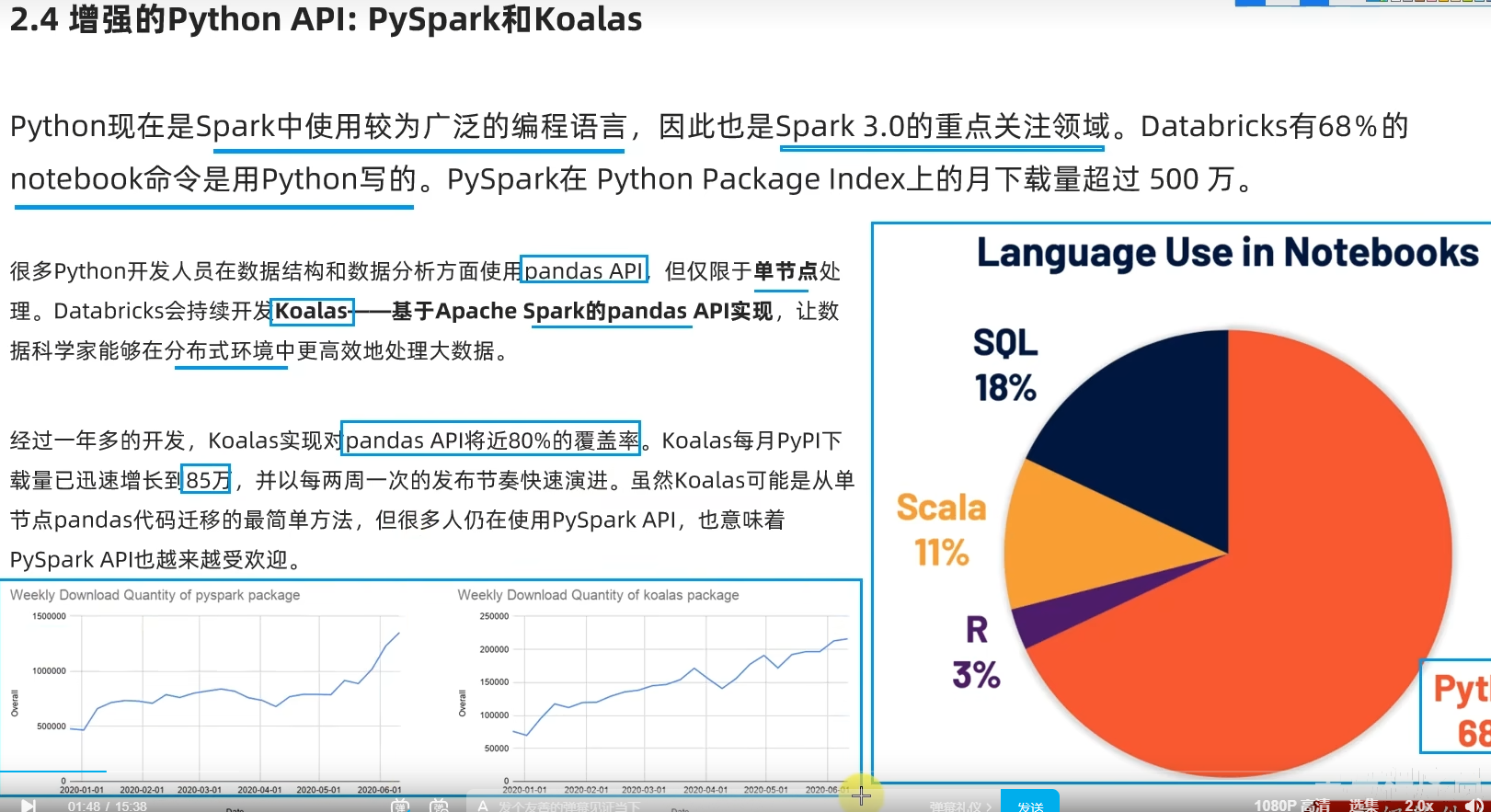
[学习笔记]黑马程序员Spark全套视频教程,4天spark3.2快速入门到精通,基于Python语言的spark教程
文章目录视频资料:一、Spark基础入门(环境搭建、入门概念)第二章:Spark环境搭建-Local2.1 课程服务器环境2.2 Local模式基本原理2.3 安装包下载2.4 Spark Local模式部署第三章:Spark环境搭建-StandAlone3.1 StandAlone…...

git push和 git pull的使用
git push与git pull是一对推送/拉取分支的git命令。git push 使用本地的对应分支来更新对应的远程分支。$ git push <远程主机名> <本地分支名>:<远程分支名>*注意: 命令中的本地分支是指将要被推送到远端的分支,而远程分支是指推送的目标分支&am…...

首发,pm3包,一个用于多组(3组)倾向评分匹配的R包
目前,本人写的第二个R包pm3包已经正式在CRAN上线,用于3组倾向评分匹配,只能3组不能多也不能少。 可以使用以下代码安装 install.packages("pm3")什么是倾向性评分匹配?倾向评分匹配(Propensity Score Match…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

