1 月 26日算法练习
文章目录
- 九宫幻方
- 穿越雷区
- 走迷宫
九宫幻方
小明最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个33的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:“二四为肩,六八为足,左三右七,戴九履一,五居其中”,通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
4 9 2
3 5 7
8 1 6
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小明准备将一个三阶幻方(不一定是上图中的那个)中的一些数抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一个解。
而你呢,也被小明交付了同样的任务,但是不同的是,你需要写一个程序~
【输入格式】
输入仅包含单组测试数据。
每组测试数据为一个33的矩阵,其中为0的部分表示被小明抹去的部分。
对于100%的数据,满足给出的矩阵至少能还原出一组可行的三阶幻方。
【输出格式】
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出“Too Many”(不包含引号)。
【样例输入】
0 7 2
0 5 0
0 3 0
【样例输出】
6 7 2
1 5 9
8 3 4
思路:dfs,回溯
#include<iostream>
#include<utility>using namespace std;int a[5][5],ans[5][5];
pair<int, int> p[10];
int n,cnt;
int vis[10];int check(){int sum = a[1][1]+a[2][2]+a[3][3];if(sum!=a[1][3]+a[2][2]+a[3][1])return 0;for(int i=1;i<=3;i++){int tmp1=0,tmp2=0;for(int j=1;j<=3;j++){tmp1+=a[i][j],tmp2+=a[j][i];}if(sum!=tmp1||sum!=tmp2)return 0;}return 1;
}void dfs(int now){if(now > n){if(check()){cnt++;for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){ans[i][j] = a[i][j];}}}return;}int x = p[now].first,y = p[now].second;for(int k=1;k<=9;k++){if(vis[k])continue;a[x][y] = k;vis[k] = 1;dfs(now + 1);a[x][y]=0;vis[k]=0;}}int main( ){for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){cin>>a[i][j];if(!a[i][j])p[++n] = make_pair(i, j);vis[a[i][j]] = 1;}}dfs(1);if(cnt==1){for(int i=1;i<=3;i++){for(int j=1;j<=3;j++){cout<<ans[i][j]<<" \n"[j==3];}}}else cout<<"Too Many\n";return 0;
}
穿越雷区
X 星的坦克战车很奇怪,它必须交替地穿越正能量辐射区和负能量辐射区才能保持正常运转,否则将报废。
某坦克需要从 A 区到 B 区去(A,B 区本身是安全区,没有正能量或负能量特征),怎样走才能路径最短?
已知的地图是一个方阵,上面用字母标出了 A,B 区,其它区都标了正号或负号分别表示正负能量辐射区。
例如:
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
坦克车只能在水平或垂直方向上移动到相邻的区。
输入格式
输入第一行是一个整数n,表示方阵的大小, 4 ≤ n < 100。
接下来是n 行,每行有n 个数据,可能是 A,B,+,- 中的某一个,中间用空格分开。
A,B 都只出现一次。
输出格式
要求输出一个整数,表示坦克从A区到B区的最少移动步数。如果没有方案,则输出-1
样例输入
5
A + - + -
- + - - +
- + + + -
+ - + - +
B + - + -
样例输入
10
dfs,剪枝
#include<iostream>
#include<utility>
using namespace std;
const int N = 1e3 + 5;
int n,ans;
pair<int,int> st,ed;
int a[N][N],vis[N][N];void dfs(int x,int y,int cnt){if(cnt>ans)return;if(cnt>vis[x][y])return;if(x>n||x<1||y<1||y>n)return;if(x==ed.first&&y==ed.second){ans=cnt;return;}vis[x][y]=cnt;int nx = x-1,ny=y;if(a[nx][y]!=a[x][y])dfs(nx,ny,cnt+1);nx = x+1,ny=y;if(a[nx][y]!=a[x][y])dfs(nx,ny,cnt+1);nx = x,ny = y-1;if(a[x][ny]!=a[x][y])dfs(nx,ny,cnt+1);nx = x,ny = y+1;if(a[x][ny]!=a[x][y])dfs(nx,ny,cnt+1);
}int main(){char x;cin>>n;ans = 0x3f3f3f3f;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)vis[i][j]=0x3f3f3f3f;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>x;if(x=='A')st.first=i,st.second=j,a[i][j]=-1;else if(x=='B')ed.first=i,ed.second=j,a[i][j]=-1;else if(x=='+')a[i][j]=1;else a[i][j]=0;}}dfs(st.first,st.second,0);cout<<ans<<'\n';return 0;
}走迷宫
给定一个 n×m 的二维整数数组,用来表示一个迷宫,数组中只包含 0 或 1,其中 0 表示可以走的路,1 表示不可通过的墙壁。
最初,有一个人位于左上角 (1,1) 处,已知该人每次可以向上、下、左、右任意一个方向移动一个位置。
请问,该人从左上角移动至右下角 (n,m) 处,至少需要移动多少次。
数据保证 (1,1) 处和 (n,m) 处的数字为 0,且一定至少存在一条通路。
输入格式
第一行包含两个整数 n 和 m。
接下来 n 行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。
输出格式
输出一个整数,表示从左上角移动至右下角的最少移动次数。
数据范围
1≤n,m≤100
输入样例:
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8
- bfs
#include<iostream>
#include<queue>
#include<utility>
#include<cstring>
using namespace std;
using PII = pair<int,int>;
const int N = 1e2+5;
int w,h;
int mp[N][N],ans[N][N];
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
void bfs(){queue<pair<int,int>> q;q.push({0,0});memset(ans,-1,sizeof(ans));ans[0][0] = 0;while(!q.empty()){PII front = q.front();q.pop();for(int k=0;k<4;k++){int nx=dx[k]+front.first,ny=dy[k]+front.second;if(nx>=0&&nx<w&&ny>=0&&ny<h&&ans[nx][ny]==-1&&mp[nx][ny]==0){ans[nx][ny]=ans[front.first][front.second]+1;q.push({nx,ny});}}}
}int main( ){cin>>w>>h;for(int i=0;i<w;i++)for(int j=0;j<h;j++)cin>>mp[i][j];bfs();cout<<ans[w-1][h-1]<<'\n';return 0;
}
相关文章:

1 月 26日算法练习
文章目录 九宫幻方穿越雷区走迷宫 九宫幻方 小明最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个33的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。 三阶幻方又被称…...
今日AI大热潮,明日智能风向标
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
03 SB实战 -微头条之首页门户模块(跳转某页面自动展示所有信息+根据hid查询文章全文并用乐观锁修改阅读量)
1.1 自动展示所有信息 需求描述: 进入新闻首页portal/findAllType, 自动返回所有栏目名称和id 接口描述 url地址:portal/findAllTypes 请求方式:get 请求参数:无 响应数据: 成功 {"code":"200","mes…...

Abaqus许可分析工具
在当今的知识产权保护和许可管理领域,一款高效、精准的许可分析工具对于企业来说至关重要。Abaqus许可分析工具凭借其强大的功能和卓越的性能,成为了企业优化知识产权许可管理的得力助手。 一、Abaqus许可分析工具的核心优势 1.全面性:Abaqus…...

【开发工具】从eclipse到idea的过度
背景 随着eclipse相比以前性能慢了不少,idea在开发工具领域越战越猛,市场份额也逐年增加,其体验得了软件工程师的热爱。 概要 本文只是做了一个简要的记录,简单描述下本人从eclipse到idea的过度的心态。 正文 在大厂都会研发自…...

【QT+QGIS跨平台编译】之十一:【libzip+Qt跨平台编译】(一套代码、一套框架,跨平台编译)
文章目录 一、libzip介绍二、文件下载三、文件分析四、pro文件五、编译实践一、libzip介绍 libzip是一个开源C库,用于读取,创建和修改zip文件。 libzip可以从数据缓冲区,文件或直接从其他zip归档文件直接复制的压缩数据中添加文件。在不关闭存档的情况下所做的更改可以还原…...
openlayers+vue实现缓冲区
文章目录 前言一、准备二、初始化地图1、创建一个地图容器2、引入必须的类库3、地图初始化4、给地图增加底图 三、创建缓冲区1、引入需要的工具类库2、绘制方法 四、完整代码总结 前言 缓冲区是地理空间目标的一种影响范围或服务范围,是对选中的一组或一类地图要素(点、线或面…...
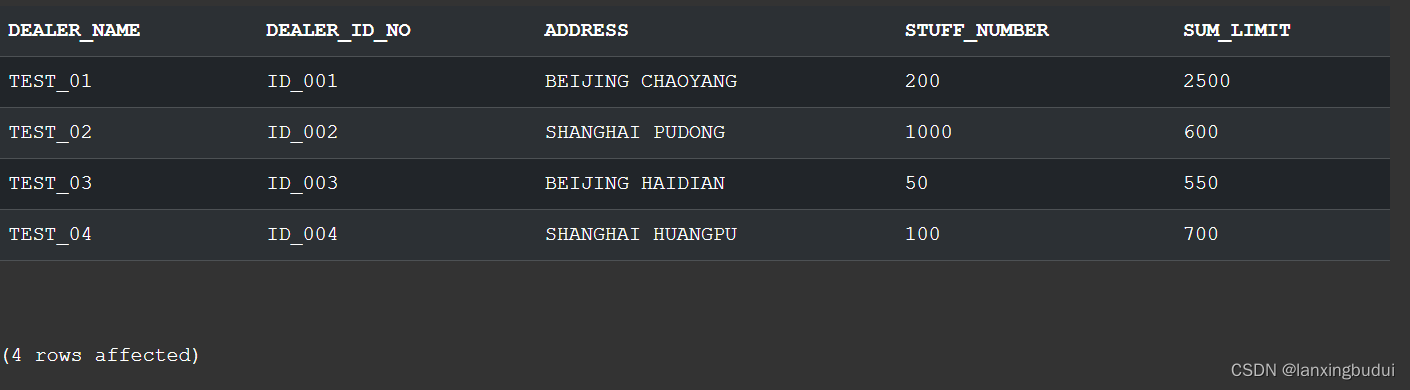
(大众金融)SQL server面试题(3)-客户已用额度总和
今天,面试了一家公司,什么也不说先来三道面试题做做,第三题。 那么,我们就开始做题吧,谁叫我们是打工人呢。 题目是这样的: DEALER_INFO经销商授信协议号码经销商名称经销商证件号注册地址员工人数信息维…...

c语言笔记
1. c语言部分算法列举 1.1 找数 二分查找(前提是数据必须有序) 1.2 求极值 1.3 数组逆序 1.4 排序法(***重点***) 1.4.1 选择排序法 1.4.2 冒泡排序法 1.4.3 插入排序法 2. 字符型数组 2.1 使用格式 char s[10]; …...

6轴机器人运动正解-逆解控制【1】——三种控制位姿的方式
概览: 通过运动学正解控制机器人运动通过运动学逆解控制机器人运动一个简单的物体搬运(沿轨迹运动) 后续会陆续更新(本例仅供学习交流用) 一、6轴机器人 二、运动正解控制 通过修改各个轴的角度,实现末…...

c# Microsoft UI Automation
Microsoft UI Automation(UIA)是一种用于自动化Windows应用程序用户界面(UI)的框架。它允许开发人员编写自动化测试脚本、辅助技术应用程序和其他需要与应用程序交互的工具。以下是一些关于Microsoft UI Automation的重要信息&…...
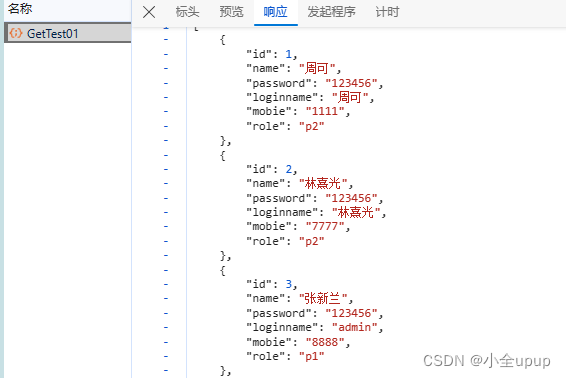
C#-前后端分离连接mysql数据库封装接口
C#是世界上最好的语言 新建项目 如下图所示选择框红的项目 然后新建 文件夹 Common 并新建类文件 名字任意 文件内容如下 因为要连接的是mysql数据库 所以需要安装 MySql.Data.MySqlClient 依赖; using MySql.Data.MySqlClient; using System.Data;namespace WebApplication1.…...

yolov8 opencv dnn部署自己的模型
源码地址 本人使用的opencv c github代码,代码作者非本人 使用github源码结合自己导出的onnx模型推理自己的视频 推理条件 windows 10 Visual Studio 2019 Nvidia GeForce GTX 1070 opencv4.7.0 (opencv4.5.5在别的地方看到不支持yolov8的推理,所以只使用opencv…...

插槽(64-67)
文章目录 插槽1.插槽 - 默认插槽(组件内可以定制一处结构)2.插槽 - 后备内容(默认值)3.插槽 - 具名插槽(组件内可以定制多处结构)4.作用域插槽(插槽的一个传参语法) 插槽 插槽分类:默认插槽和具名插槽 1.插槽 - 默认插槽(组件内可以定制一处结构) 作用…...

C# LING查询语法学习,扩展方法的使用
class Program { #region 示例1:不使用LINQ查询数组 //static void Main(string[] args) //{ // int[] nums { 1, 7, 2, 6, 5, 4, 9, 13, 20 }; // List<int> list new List<int>(); // foreach (int item in nums) …...
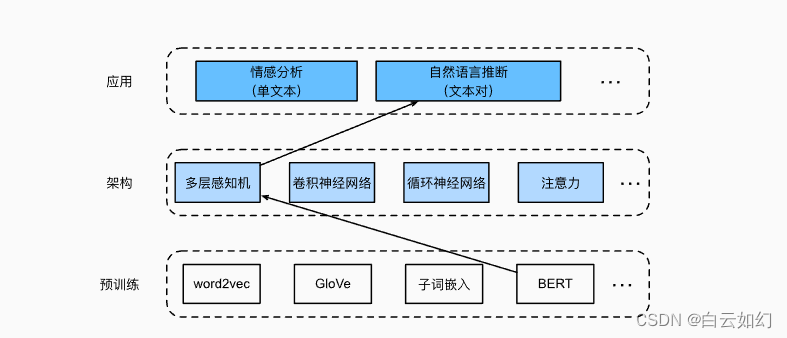
自然语言推断:微调BERT
微调BERT 自然语言推断任务设计了一个基于注意力的结构。现在,我们通过微调BERT来重新审视这项任务。自然语言推断是一个序列级别的文本对分类问题,而微调BERT只需要一个额外的基于多层感知机的架构,如下图中所示。 本节将下载一个预训练好的…...
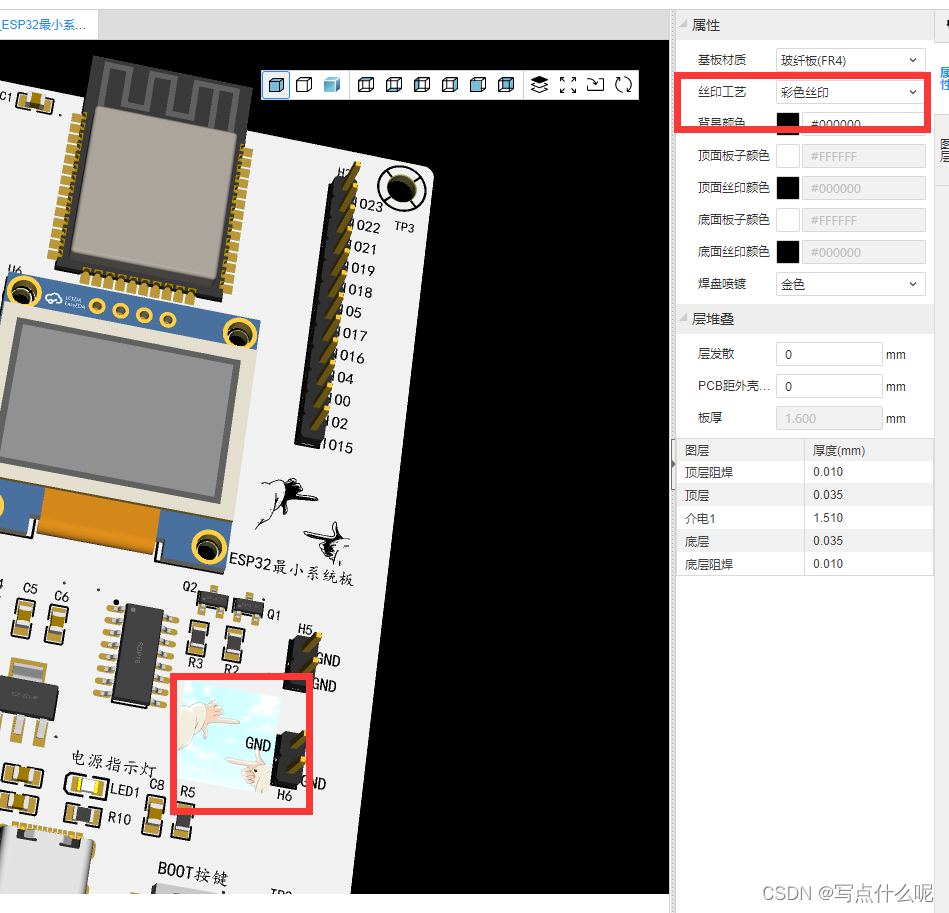
立创EDA学习:设计收尾工作
布线整理 ShiftM,关闭铺铜显示 调整结束后再使用快捷键”ShiftM“打开铺铜 过孔 在空白区域加上一些GND过孔,连接顶层与底层的铺铜。放置好”过孔“后,隐藏铺铜,观察刚才放置的过孔有没有妨碍到其他器件 调整铺铜 先打开铺铜区&…...

ShardingSphere之ShardingJDBC客户端分库分表上
目录 什么是ShardingSphere? 客户端分库分表与服务端分库分表 ShardingJDBC客户端分库分表 ShardingProxy服务端分库分表 ShardingSphere实现分库分表的核心概念 ShardingJDBC实战 什么是ShardingSphere? ShardingSphere是一款起源于当当网内部的应…...

rust for循环步长-1,反向逆序遍历
fn main() {for i in (0..3).rev().step_by(1) {print!("{}", i);} } // 打印结果:210Trait std::iter::Iterator fn rev(self) -> Rev< Self > where Self: Sized DoubleEndedIteratorfn step_by(self, step: usize) -> StepBy< Self &…...
)
编译与运行环境(C语言)
文章目录 前言编译环境编译链接 运行环境 前言 C语言代码的实现,存在两种不同的环境。 第一种是翻译环境,在这个环境中,源代码被转换为可执行的二进制指令。 翻译环境即我们日常使用编译器,将一个 " mission.c " 的文件…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...
