5-2、S曲线计算【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章
摘要:本节介绍S曲线的基本变换,将基本形式的S曲线变换成为任意过两点的S曲线,为后续步进电机S曲线运动提供理论支撑
一.计算目标
①计算经过任意不同两点的S曲线方程
②可调节曲线平滑度
③可调节曲线对称度
④绘制其图像
二.计算过程
2.1 S曲线基本形式


2.2 S曲线变换
第一步:进行X轴比例变换,比例系数为N(N≠0)
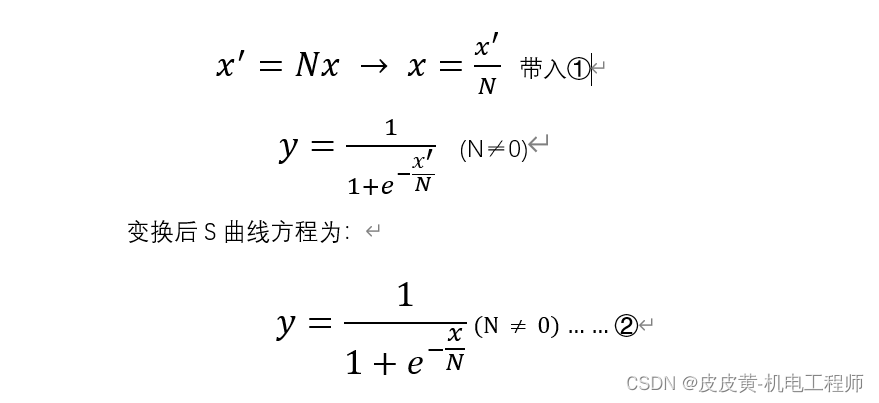
第二步:进行X轴平移变换,平移系数为A

第三步:进行Y轴比例变换,比例系数为K(K≠0)

第四步:进行Y轴平移变换,平移系数为B

最终得到S曲线变换之后函数关系式:

2.3 参数计算
要求变换之后的S曲线经过P1(X1,Y1),P2(X2,Y2)两点,可建立方程
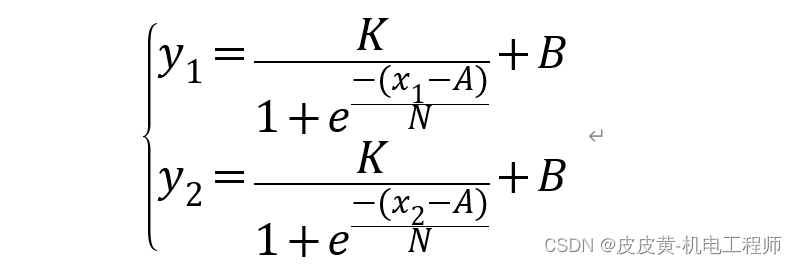
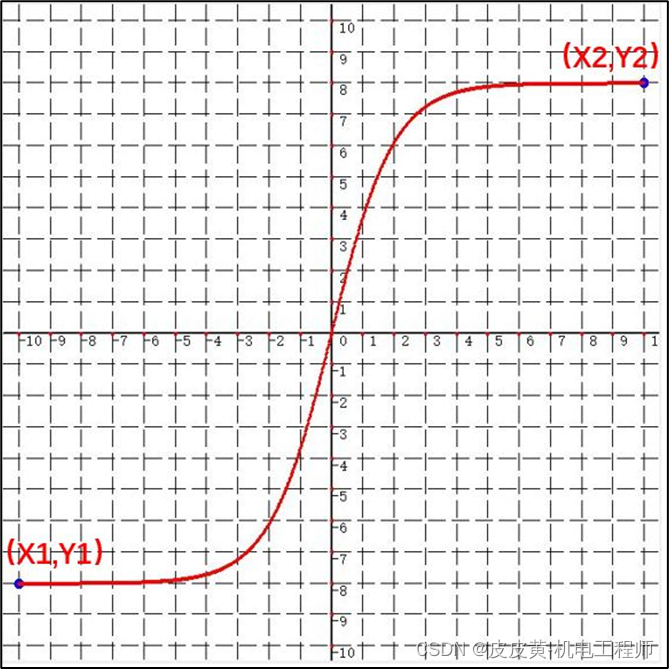
方程有N,K,A,B四个未知数,需要给定2个参数由用户设定,此处选择N,A,则可求得K,B值为:

其中N值作为X轴方向比例变换系数,N>1时,S曲线X方向放大,N<1时,S曲线X方向缩小,可以将N值等效为S曲线的平滑度调节参数
其中A值X轴方向平移系数,A>0时,S曲线向X正方向平移,A<0时,S曲线向X负方向平移,可以将A值等效为S曲线的对称度调节参数
2.4中心对称条件
当随意给定N,A值时,S曲线容易出现失真,如下图所示
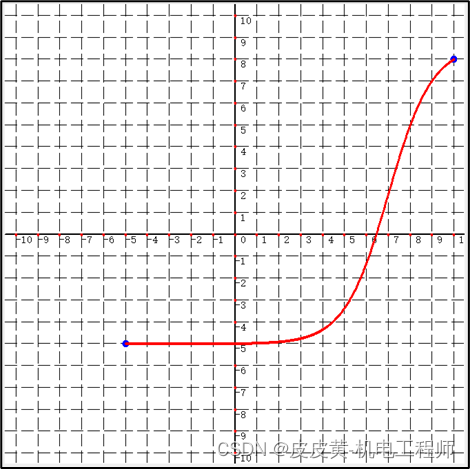
为确保经过P1,P2两点的S曲线也为中心对称,则要求S曲线经过P1P2连线的中点P0(X0,Y0),如图所示

则可建立三个等式
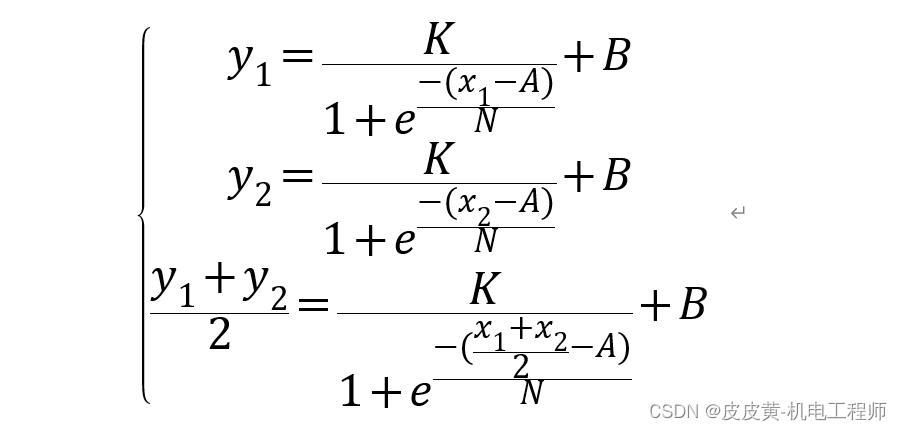
N由用户设定,可求得A值

三.总结
通过上述计算,完成了目标中的4点要求。在不同的应用场景中,可以根据实际情况去对该S曲线进行灵活处理。S曲线代表的v-t图像中对其进行求导可以求得a-t关系
四.附件
提供一个S曲线的演示器,下载请见百度网盘链接
链接:https://pan.baidu.com/s/1A6_d9DYztqIgNV5AMRlTPw
提取码:l3qi
相关文章:

5-2、S曲线计算【51单片机+L298N步进电机系列教程】
↑↑↑点击上方【目录】,查看本系列全部文章 摘要:本节介绍S曲线的基本变换,将基本形式的S曲线变换成为任意过两点的S曲线,为后续步进电机S曲线运动提供理论支撑 一.计算目标 ①计算经过任意不同两点的S曲线方程 ②可调节曲线平…...

SQL 注入 - http头注入之UA头注入探测
环境准备:构建完善的安全渗透测试环境:推荐工具、资源和下载链接_渗透测试靶机下载-CSDN博客 一、http头注入介绍 HTTP头注入是一种网络安全攻击手段,它利用了Web应用程序对HTTP头的处理不当或缺乏充分的验证和过滤。在这种攻击中,攻击者通过修改HTTP请求头中的某些字段,…...

学习数据结构和算法的第5天
空间复杂度及其常见案例 空间复杂度 空间复杂度也是一个数学函数表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。 空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度…...
 root方式)
Android 11 访问 Android/data/或者getExternalCacheDir() root方式
前言: 需求要求安装三方应用ExternalCacheDir()下载下来的apk文件。 getExternalCacheDir() : /storage/emulated/0/Android/data/com../cache/ 获取访问权限 如果手机安卓版本为Android10的时候,可以在AndroidManifest.xml中添加下列代码 android:requestLegacyExt…...
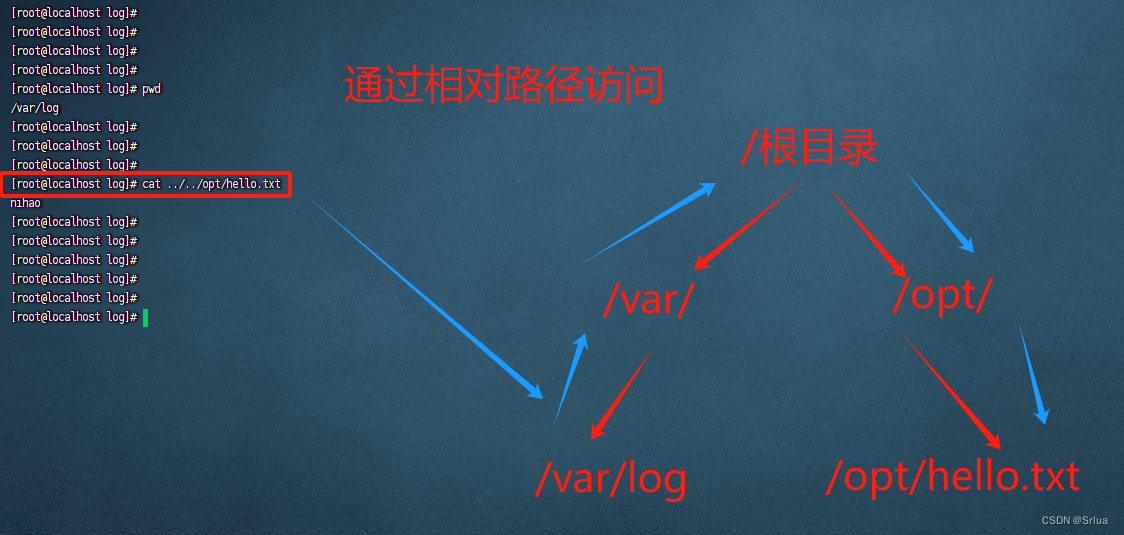
Linux探秘之旅:透彻理解路径、命令与系统概念
目录 如何远程连接 远程登录简明指南 linux区别 1.严格区分大小写 2.linux的命令返回结果判断 3.如何查看网络信息 4.关于后缀名(Linux不关心文件后缀) 4.1 需要记忆的后缀 5.echo命令 6.linux一切皆文件 6.1比如磁盘的文件 6.2可执行文件 …...

哈希算法 c语言
#include <stdio.h> #include <stdlib.h> #include <string.h> // 哈希函数 unsigned int hash_function(const char *str) { unsigned int hash 0; while (*str) { hash (hash * 31 *str) % 1000; str; } return hash;…...

新版MQL语言程序设计:组合模式的原理、应用及代码实现
文章目录 一、什么组合模式二、为什么需要组合模式三、组合模式的实现原理四、组合模式的应用场景五、组合模式的代码实现 一、什么组合模式 组合模式是一种结构型设计模式,它允许将对象组合成树形结构以表示“部分-整体”的层次结构。组合模式使得用户对单个对象和…...
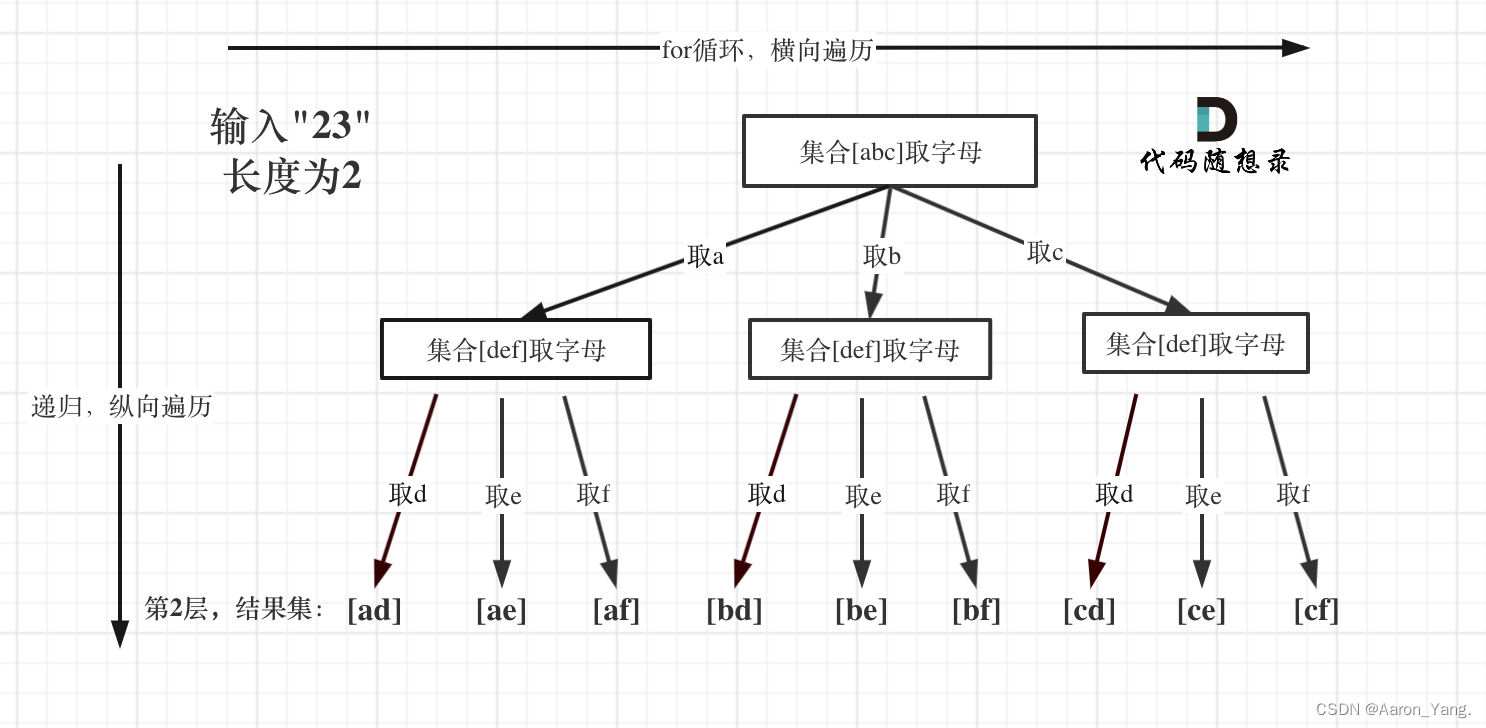
代码随想录算法训练营第25天 | 216.组合总和III ,17.电话号码的字母组合
回溯章节理论基础: https://programmercarl.com/%E5%9B%9E%E6%BA%AF%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 216.组合总和III 题目链接:https://leetcode.cn/problems/combination-sum-iii/ 思路: 本题就是在[1,2,3,4,5,6,7,…...
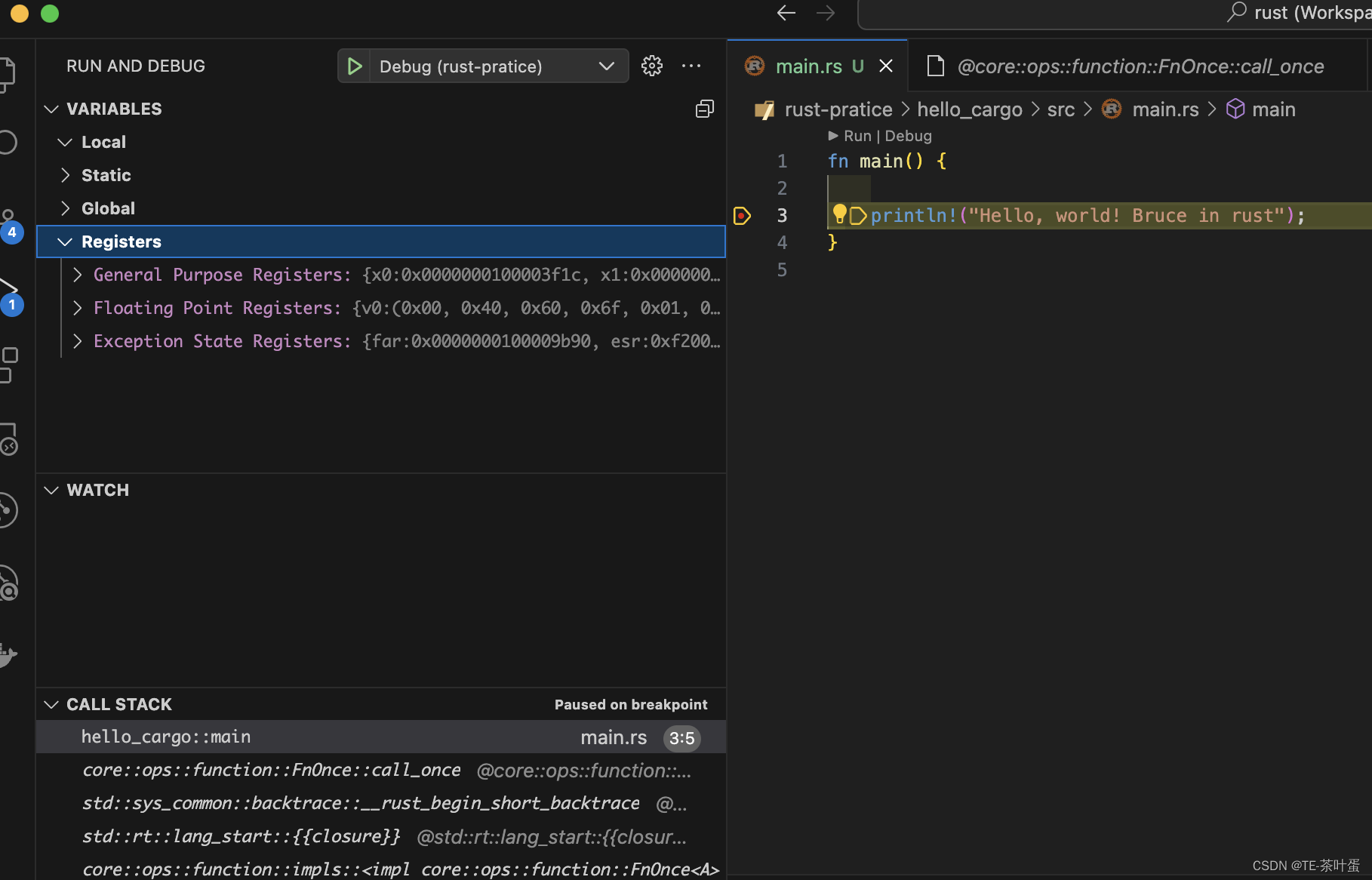
Rust 第一个rust程序Hello Rust️
文章目录 前言一、vscode 安装rust相关插件二、Cargo New三、vscode调试rustLLDB 前言 Rust学习系列。今天就让我们掌握第一个rust程序。Hello Rust 🦀️。 在上一篇文章我们在macOS成功安装了rust。 一、vscode 安装rust相关插件 以下是一些常用的 Rust 开发插件…...
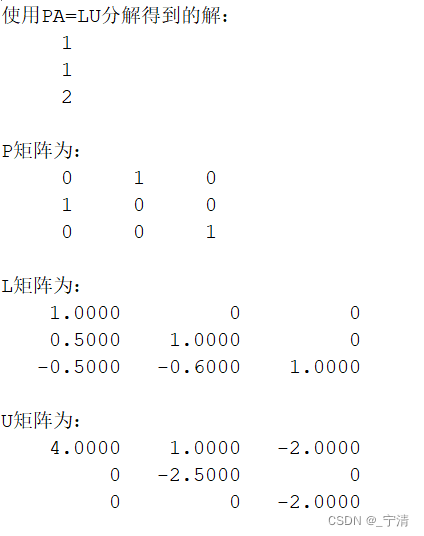
高斯消去法 | LU分解 | PA=LU分解(MatLab)
一、问题描述 利用高斯消去法,LU 分解及PALU 分解求解非线性方程组。 二、实验目的 掌握高斯消去法、LU 分解、PALU 分解的算法原理;编写代码实现利用高斯消去法、LU 分解、PALU 分解来求解线性方程组。 三、实验内容及要求 1. 利用顺序高斯消去法求…...

Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号
Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号 code review! 文章目录 Linux笔记之expect和bash脚本监听输出并在匹配到指定字符串时发送中断信号1.expect2.bash 1.expect 在Expect脚本中,你可以使用expect来监听程序输出,…...

项目02《游戏-12-开发》Unity3D
基于 项目02《游戏-11-开发》Unity3D , 任务:实现场景怪物自动巡航 , 首先在场景中创建小球命名为路径点WayPoint0, 取消小球的碰撞器Collider, 再复制两个改名为WayPoint1 和 WayPoint2 , 在…...

记一次面试题
1.Php 私有化包(composer)的部署 1. 创建你的PHP包 确定你的包的功能和命名空间。 创建一个新的目录并初始化一个Git仓库。 使用composer init命令创建一个composer.json文件,并定义你的包名、版本、依赖等信息。 2. 开发并测试你的包 在本地…...

Rust入门2——随机数
文章目录 一、生成随机数二、比较两个数相等 简单列出两个Rust的小例子 一、生成随机数 在Cargo.toml的dependencies中引入rand,指定rand的版本 [dependencies] rand "^0.3.14"之后在主函数中调用rand函数,生成随机数 use rand::Rng; f…...

c#: 表达式树的简化
环境: .net 6 一、问题? 有下面的表达式: var nums new List<int> { 1, 2, 3 }; Expression<Func<int, bool>> exp i > i > nums.Max();我们知道,它其实就是:exp i > i > 3; 那么…...
13. UE5 RPG限制Attribute的值的范围以及生成结构体
前面几章,我们实现了通过GameplayEffect对Attribute值的修改,比如血量和蓝量,我们都是有一个最大血量和最大蓝量去限制它的最大值,而且血量和蓝量最小值不会小于零。之前我们是没有实现相关限制的,接下来,我…...

UE4运用C++和框架开发坦克大战教程笔记(十九)(第58~60集)完结
UE4运用C和框架开发坦克大战教程笔记(十九)(第58~60集)完结 58. 弹窗显示与隐藏59. UI 面板销毁60. 框架完成与总结 58. 弹窗显示与隐藏 这节课我们先来补全 TransferMask() 里对于 Overlay 布局类型面板的遮罩转移逻辑ÿ…...

ModuleNotFoundError: No module named ‘_ctypes‘报错解决方案
1、须命令安装libbffi-devel软件包: yum install libffi-devel -y2、安装完后再重装python3,无须卸载 找到之前的python3安装包,如果安装包删除了通过 history | grep python命令找到最初安装时的包下载的命令下载,保证版本一样&…...

【服务器数据恢复】服务器RAID模块硬件损坏的数据恢复案例
服务器数据恢复环境&故障: 某品牌服务器中有一组由数块SAS硬盘组建的RAID5磁盘阵列,服务器操作系统是WINDOWS SERVER,服务器中存放企业数据,无数据库文件。 服务器出故障之前出现过几次意外断电的情况,服务器断电…...

spring boot3x登录开发-上(整合jwt)
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 jwt简介 导依赖 编写jwt工具类 1.配置项直接嵌入代码,通过类名.静态方法使用 2.配置项写到…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...
