Codeforces Round 240 (Div. 1) C. Mashmokh and Reverse Operation(分治+逆序对)
原题链接:C. Mashmokh and Reverse Operation
题目大意:
给出一个长度为 2 n 2^{n} 2n 的正整数数组 a a a ,再给出 m m m 次操作。
每次操作给出一个数字 q q q ,把数组分为 2 n − q 2^{n-q} 2n−q 个长度为 2 q 2^{q} 2q 的段,然后每段执行一次翻转操作,操作完后输出当前数组的逆序对数量。
分段操作: [ a 1 , a 2 , . . . , a 2 q ] , [ a 2 q + 1 , a 2 q + 2 , . . . , a 2 q + 1 ] , . . . , [ a 2 n − 1 + 1 , a 2 n − 1 + 2 , . . . , a 2 n ] [a_{1},a_{2},...,a_{2^q}],[a_{2^{q}+1},a_{2^{q}+2},...,a_{2^{q+1}}],...,[a_{2^{n-1}+1},a_{2^{n-1}+2},...,a_{2^{n}}] [a1,a2,...,a2q],[a2q+1,a2q+2,...,a2q+1],...,[a2n−1+1,a2n−1+2,...,a2n]
翻转操作: [ a 2 q , a 2 q − 1 , . . . , a 1 ] , [ a 2 q + 1 , a 2 q − 1 , . . . , a 2 q + 1 ] , . . . , [ a 2 n , a 2 n − 1 , . . . , a 2 n − 1 + 1 ] [a_{2^{q}},a_{2^{q}-1},...,a_{1}],[a_{2^{q+1}},a_{2^{q}-1},...,a_{2^{q}+1}],...,[a_{2^{n}},a_{2^{n}-1},...,a_{2^{n-1}+1}] [a2q,a2q−1,...,a1],[a2q+1,a2q−1,...,a2q+1],...,[a2n,a2n−1,...,a2n−1+1]
每次操作会改变原数组,并且都要输出操作完后逆序对的数量。
解题思路:
很有意思的分治归并排序题。
首先发现我们数组长度是 2 2 2 的次幂,且每次分段长度也都是 2 2 2 的次幂,暗示我们可以向着分治的方向去思考。
我们知道:逆序对 + + + 顺序对 = n ⋅ ( n − 1 ) 2 =\frac{n \cdot(n-1)}{2} =2n⋅(n−1) 其中 n n n 为区间长度。
我们将一个区间翻转时,本质上就是将逆序对的值和顺序对的值交换了一下,因为本来逆序的翻转之后就变成顺序的了。
这样类似将数组分成一段段的 2 2 2 次幂长度,我们考虑可以考虑类似归并排序的分治方法。
归并排序是在排序的过程中同时算出每一层的逆序对,然后相加每层得到的逆序对,从而得到整个原数组的逆序对的。
假设原数组 a a a 为 [ 4 , 5 , 7 , 1 , 3 , 6 , 8 , 2 ] [4,5,7,1,3,6,8,2] [4,5,7,1,3,6,8,2] ,我们画出归并排序树看看:
3 : [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ] 7 3:[1,2,3,4,5,6,7,8]^{7} 3:[1,2,3,4,5,6,7,8]7
2 : [ 1 , 4 , 5 , 7 ] 2 , [ 2 , 3 , 6 , 8 ] 2 2:[1,4,5,7]^{2},[2,3,6,8]^{2} 2:[1,4,5,7]2,[2,3,6,8]2
1 : [ 4 , 5 ] 0 , [ 1 , 7 ] 1 , [ 3 , 6 ] 0 , [ 2 , 8 ] 1 1:[4,5]^{0},[1,7]^{1},[3,6]^{0},[2,8]^{1} 1:[4,5]0,[1,7]1,[3,6]0,[2,8]1
0 : [ 4 ] , [ 5 ] , [ 7 ] , [ 1 ] , [ 3 ] , [ 6 ] , [ 8 ] , [ 2 ] 0:[4],[5],[7],[1],[3],[6],[8],[2] 0:[4],[5],[7],[1],[3],[6],[8],[2]
(右上角角标为将该层排好序时得到的逆序对数量,叶子层(第 0 0 0 层)均为 0 0 0 就不做标记了)
那么总的逆序对数就是所有层角标相加之和: 7 + 2 + 2 + 0 + 1 + 0 + 1 = 13 7+2+2+0+1+0+1=13 7+2+2+0+1+0+1=13 对。
我们考虑将区间长度为 2 1 2^{1} 21 的段全翻转,看看会造成什么影响。
3 : [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ] 7 3:[1,2,3,4,5,6,7,8]^{7} 3:[1,2,3,4,5,6,7,8]7
2 : [ 1 , 4 , 5 , 7 ] 2 , [ 2 , 3 , 6 , 8 ] 2 2:[1,4,5,7]^{2},[2,3,6,8]^{2} 2:[1,4,5,7]2,[2,3,6,8]2
1 ′ : [ 4 , 5 ] 1 , [ 1 , 7 ] 0 , [ 3 , 6 ] 1 , [ 2 , 8 ] 0 1':[4,5]^{1},[1,7]^{0},[3,6]^{1},[2,8]^{0} 1′:[4,5]1,[1,7]0,[3,6]1,[2,8]0
0 ′ : [ 5 ] , [ 4 ] , [ 1 ] , [ 7 ] , [ 6 ] , [ 3 ] , [ 2 ] , [ 8 ] 0':[5],[4],[1],[7],[6],[3],[2],[8] 0′:[5],[4],[1],[7],[6],[3],[2],[8]
那么总的逆序对数就是 7 + 2 + 2 + 1 + 0 + 1 + 0 = 13 7+2+2+1+0+1+0=13 7+2+2+1+0+1+0=13 对。
可以发现,我们只有在第 1 → 0 1 \rightarrow 0 1→0 层往下的所有层逆序对被改变了,即顺序对和逆序对交换了,而其他层 n → 2 n \rightarrow 2 n→2 层则无变化。
因为归并到第 0 → i 0 \rightarrow i 0→i 层前,其下的所有层是在做 边排序边计算 的过程,因此无论其下层的顺序是怎么样的,最终数组 排序 到到第 i i i 层时的状态都是唯一确定的,不会影响到上一层。
比如我们修改前的第 1 1 1 层,和我们原数组的第 1 1 1 层状态是相同的,只有逆序对和顺序对的角标被改变了。
同理,无论按何种顺序如何翻转第 2 q 2^{q} 2q 层,其只会影响第 0 → q 0 \rightarrow q 0→q 的逆序对状态,而不会影响第 q + 1 → n q+1 \rightarrow n q+1→n 层逆序对的状态。
因此,我们先对原数组做一次归并排序,同时记录每一层的逆序对状态,和顺序对状态。
对每次的修改,对 1 → q 1 \rightarrow q 1→q 层直接交换顺序对和逆序对的值(第 0 0 0 层全是 0 0 0 ,可以不管),其余不变(或者用 2 n − q ⋅ 2 q ⋅ ( 2 q − 1 ) 2 − 2^{n-q} \cdot \frac{2^{q} \cdot (2^{q}-1)}{2}- 2n−q⋅22q⋅(2q−1)−当前层逆序对之和,不过有个 2 2 2 的次幂,比较麻烦)。
交换完后,统计所有层的逆序对之和就是我们的答案了。
时间复杂度: O ( n log n + q log n ) O(n \log n+q \log n) O(nlogn+qlogn)
AC代码:
#include <bits/stdc++.h>
using namespace std;using PII = pair<int, int>;
using i64 = long long;void solve() {int n;cin >> n;vector<int> a((1 << n) + 1);for (int i = 1; i <= (1 << n); ++i) {cin >> a[i];}vector cnt(n + 1, vector<i64>(2));vector<int> b(1 << n);auto Msort = [&](auto self, int l, int r, int dep) -> void {if (l >= r) return;int mid = l + r >> 1, i = l, j = mid + 1, k = 0;self(self, l, mid, dep - 1), self(self, mid + 1, r, dep - 1);//求顺序对while (i <= mid && j <= r) {if (a[i] < a[j]) {cnt[dep][1] += r - j + 1;++i;} else {++j;}}//求逆序对并同时将数组排序i = l, j = mid + 1;while (i <= mid && j <= r) {if (a[i] > a[j]) {cnt[dep][0] += mid - i + 1;b[k++] = a[j++];} else {b[k++] = a[i++];}}while (i <= mid) {b[k++] = a[i++];}while (j <= r) {b[k++] = a[j++];}for (i = l, j = 0; i <= r; ++i, ++j) {a[i] = b[j];}};Msort(Msort, 1, 1 << n, n);int q;cin >> q;for (int i = 1; i <= q; ++i) {int d;cin >> d;i64 ans = 0;//修改d层 则将 [1, d] 层的值全部交换一下for (int j = 1; j <= n; ++j) {if (j <= d) {swap(cnt[j][0], cnt[j][1]);}ans += cnt[j][0];}cout << ans << '\n';}
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);int t = 1; //cin >> t;while (t--) solve();return 0;
}
相关文章:
 C. Mashmokh and Reverse Operation(分治+逆序对))
Codeforces Round 240 (Div. 1) C. Mashmokh and Reverse Operation(分治+逆序对)
原题链接:C. Mashmokh and Reverse Operation 题目大意: 给出一个长度为 2 n 2^{n} 2n 的正整数数组 a a a ,再给出 m m m 次操作。 每次操作给出一个数字 q q q ,把数组分为 2 n − q 2^{n-q} 2n−q 个长度为 2 q 2^{q} 2…...
SpringBoot整合JDBC(一)JDBC组件的自动装配)
SpringBoot源码解读与原理分析(三十二)SpringBoot整合JDBC(一)JDBC组件的自动装配
文章目录 前言第10章 SpringBoot整合JDBC10.1 SpringBoot整合JDBC的项目搭建10.1.1 初始化数据库10.1.2 整合项目10.1.2.1 导入JDBC和MySQL驱动依赖10.1.2.2 配置数据源 10.1.3 编写业务代码10.1.3.1 编写与t_user表对应的实体类User10.1.3.2 编写Dao层代码10.1.3.3 编写Servic…...
petalinux_zynq7 驱动DAC以及ADC模块之五:nodejs+vue3实现web网页波形显示
前文: petalinux_zynq7 C语言驱动DAC以及ADC模块之一:建立IPhttps://blog.csdn.net/qq_27158179/article/details/136234296petalinux_zynq7 C语言驱动DAC以及ADC模块之二:petalinuxhttps://blog.csdn.net/qq_27158179/article/details/1362…...

Android java中内部类的使用
一.成员内部类 实验1:成员内部类 class Outer {private int a 10;class Inner {public void printInfo(){System.out.println("a "a);}}}public class InnerDemo {public static void main(String args[]) {Outer o new Outer();Outer.Inner i o.new…...
llm的inference(二)
文章目录 Tokenizer分词1.单词分词法2.单字符分词法3.子词分词法BPE(字节对编码,Byte Pair Encoding)WordPieceUnigram Language Model(ULM) embedding的本质推理时的一些指标参考链接 Tokenizer 在使用模型前,都需要将sequence过一遍Tokenizer…...

pytorch -- torch.nn.Module
基础 torch.nn 是 PyTorch 中用于构建神经网络的模块。nn.Module包含网络各层的定义及forward方法。 在用户自定义神经网络时,需要继承自nn.Module类。通过继承 nn.Module 类,您可以创建自己的神经网络模型,并定义模型的结构和操作。 torch.n…...

Microsoft Edge 越用越慢、超级卡顿?网页B站播放卡顿?
记录10个小妙招 Microsoft Edge 启动缓慢、菜单导航卡顿、浏览响应沉闷?这些情况可能是由于系统资源不足或浏览器没及时更新引起的。接下来,我们将介绍 10 种简单的方法,让 Edge 浏览器的速度重新起飞。 基础检查与问题解决 如果 Microsoft…...

XGB-9: 分类数据
从1.5版本开始,XGBoost Python包为公共测试提供了对分类数据的实验性支持。对于数值数据,切分条件被定义为 v a l u e < t h r e s h o l d value < threshold value<threshold ,而对于分类数据,切分的定义取决于是否使用…...

FreeRTOS学习第8篇--同步和互斥操作引子
目录 FreeRTOS学习第8篇--同步和互斥操作引子同步和互斥概念实现同步和互斥的机制PrintTask_Task任务相关代码片段CalcTask_Task任务相关代码片段实验现象本文中使用的测试工程 FreeRTOS学习第8篇–同步和互斥操作引子 本文目标:学习与使用FreeRTOS中的同步和互斥操…...
,c++STL算法的理解与使用(sort, find, binary_search等))
c++STL容器的使用(vector, list, map, set等),c++STL算法的理解与使用(sort, find, binary_search等)
cSTL容器的使用(vector, list, map, set等) 在C的STL(Standard Template Library)中,容器是重要的一部分,它们提供了各种数据结构来存储和管理数据。以下是一些常见的STL容器及其使用方法的简要说明&#x…...

选择VR全景行业,需要了解哪些内容?
近年来,随着虚拟现实、增强现实等技术的持续发展,VR全景消费市场得以稳步扩张。其次,元宇宙行业的高速发展,也在进一步拉动VR全景技术的持续进步,带动VR产业的高质量发展。作为一种战略性的新兴产业,国家和…...

830. 单调栈
Problem: 830. 单调栈 文章目录 思路解题方法复杂度Code 思路 这是一个单调栈的问题。单调栈是一种特殊的栈结构,它的特点是栈中的元素保持单调性。在这个问题中,我们需要找到每个元素左边第一个比它小的元素,这就需要使用到单调递增栈。 我们…...

H5 个人引导页官网型源码
H5 个人引导页官网型源码 源码介绍:源码无后台、无数据库,H5自检测适应、无加密,直接修改可用。 源码含有多选项,多功能。可展示自己站点、团队站点。手机电脑双端。 下载地址: https://www.changyouzuhao.cn/1434.…...
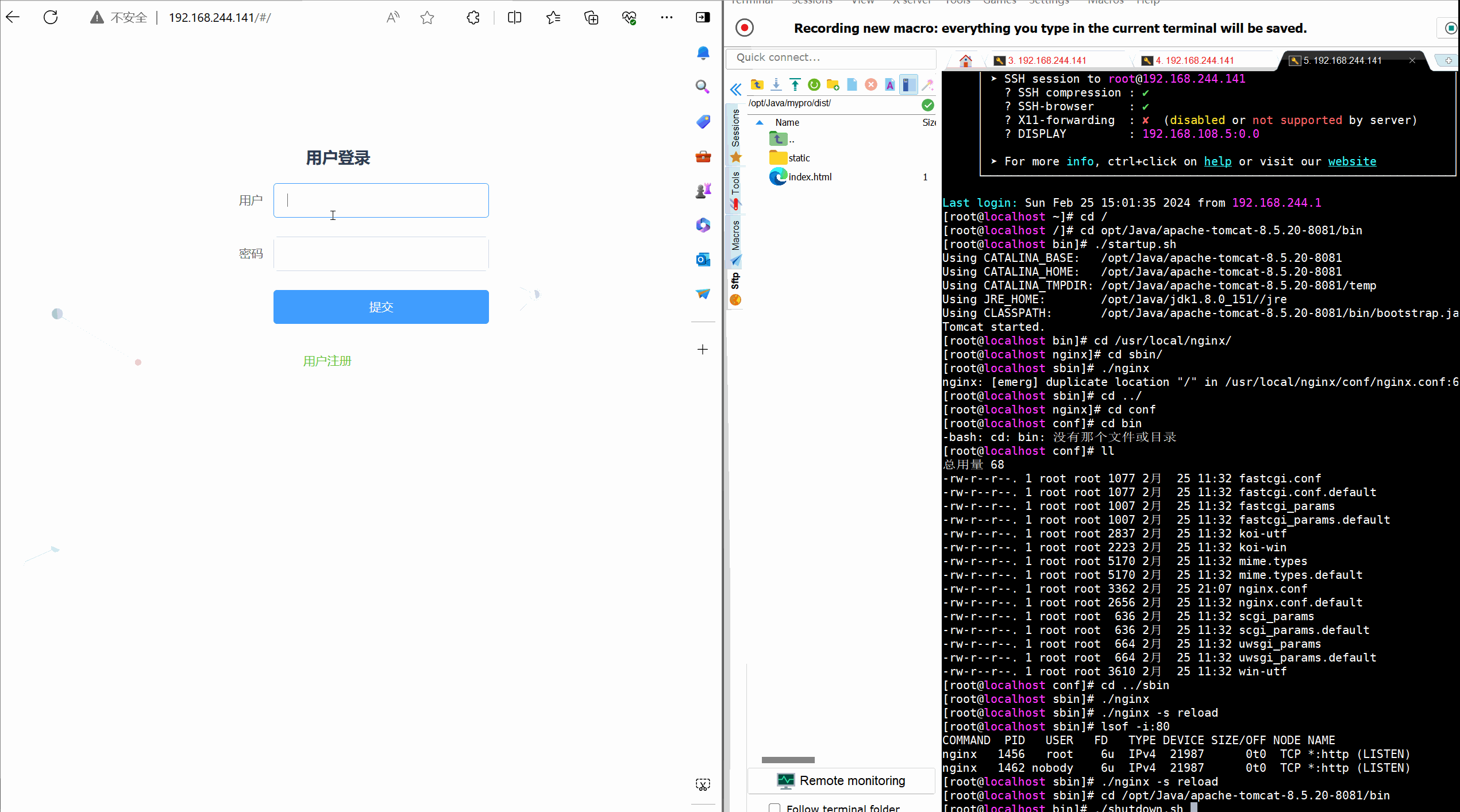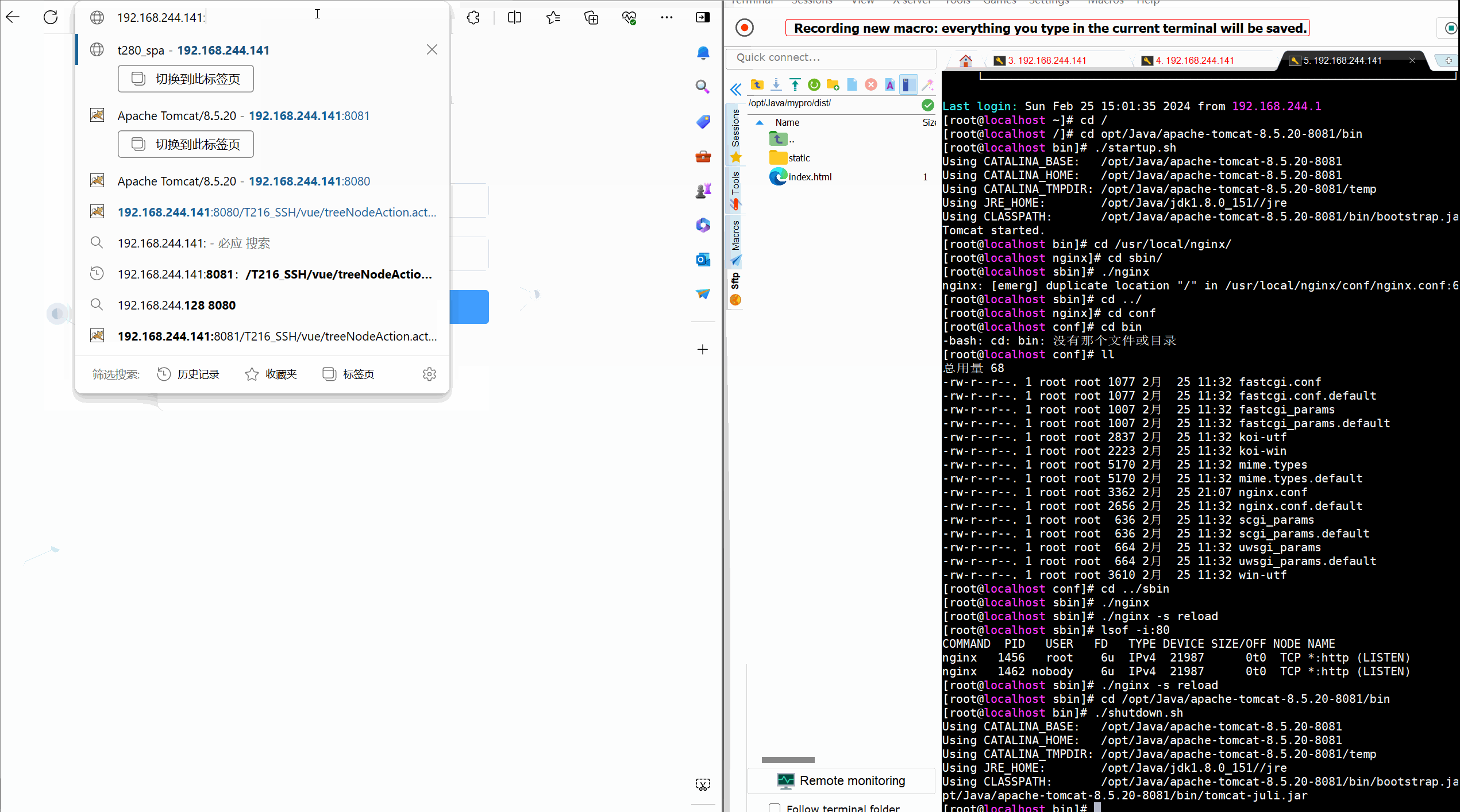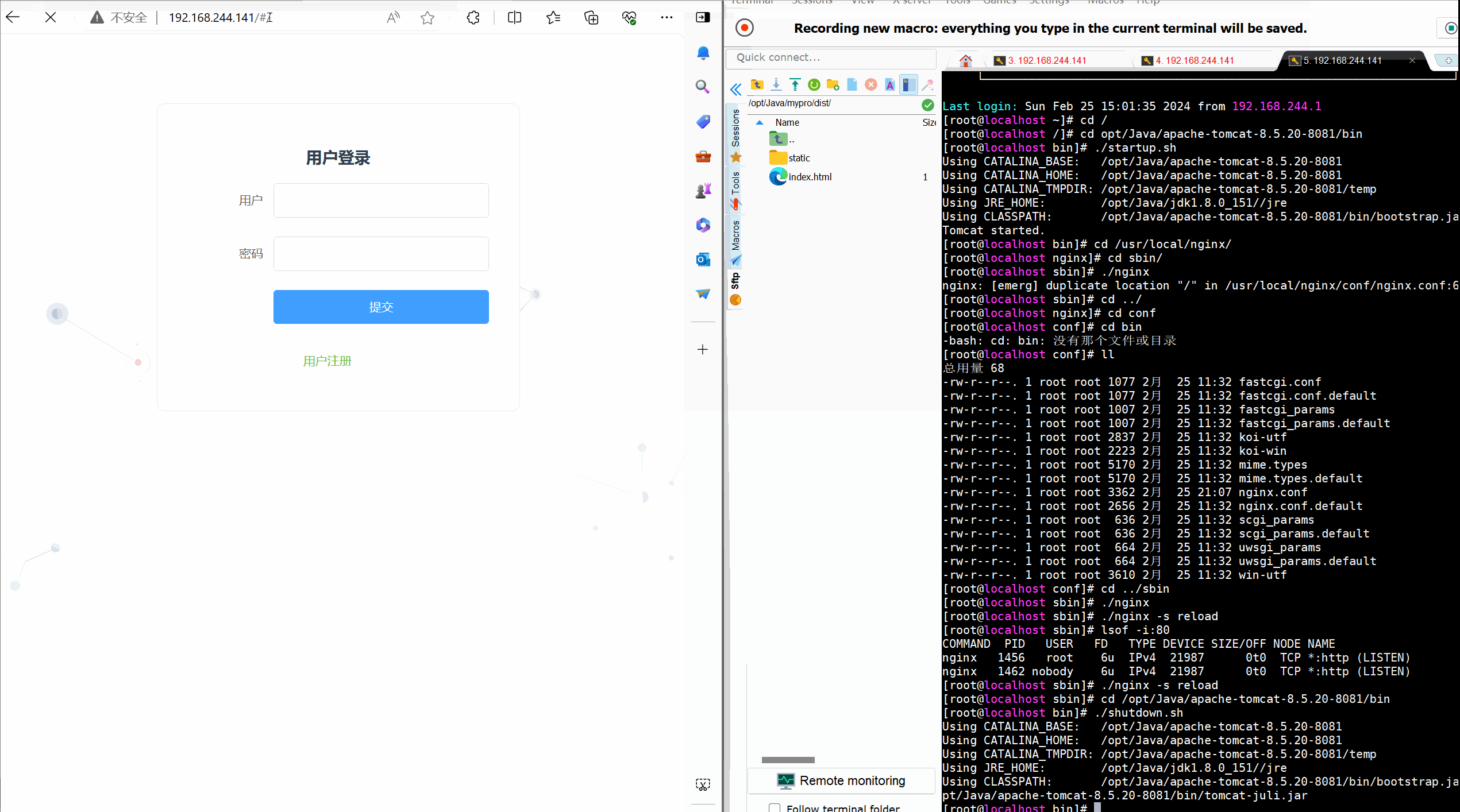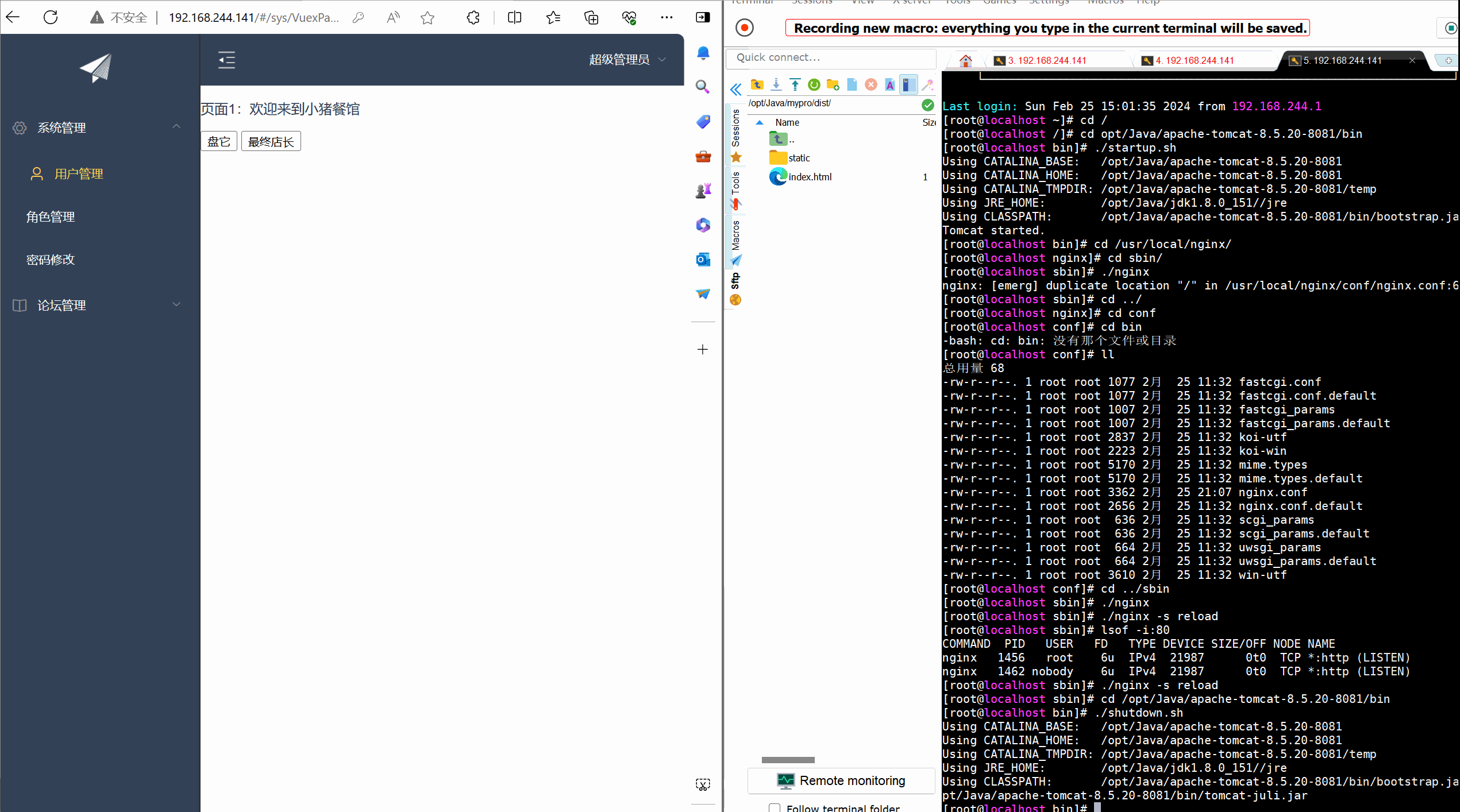
【Linux】部署前后端分离项目---(Nginx自启,负载均衡)
目录 前言 一 Nginx(自启动) 2.1 Nginx的安装 2.2 设置自启动Nginx 二 Nginx负载均衡tomcat 2.1 准备两个tomcat 2.1.1 复制tomcat 2.1.2 修改server.xml文件 2.1.3 开放端口 2.2 Nginx配置 2.2.1 修改nginx.conf文件 2.2.2 重启Nginx服务 2…...
WPF Style样式设置
1.本window设置样式 <Window x:Class"WPF_Study.MainWindow"xmlns"http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x"http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d"http://schemas.microsoft.com/expressi…...

【STM32】软件SPI读写W25Q64芯片
目录 W25Q64模块 W25Q64芯片简介 硬件电路 W25Q64框图 Flash操作注意事项 状态寄存器 编辑 指令集 INSTRUCTIONS编辑 编辑 SPI读写W25Q64代码 硬件接线图 MySPI.c MySPI.h W25Q64 W25Q64.c W25Q64.h W25Q64_Ins.h main.c 测试 SPI通信(W25…...

普通中小学校管理信息系统V1.1
普通中小学校管理信息系统 Ordinary Primary and Secondary Schools Management Information System 普通中小学校管理信息系统 Ordinary Primary and Secondary Schools Management Information System...

中国水果采摘机器人行业市场研究及发展趋势分析报告
全版价格:壹捌零零 报告版本:下单后会更新至最新版本 交货时间:1-2天 第一章 2016-2026年中国水果采摘机器人行业总概 1.1 中国水果采摘机器人行业发展概述 机器人技术的发展是一个国家高科技水平和工业自动化程度的重要标志和体现。机器…...

Linux多进程与信号
在多进程的服务程序中,如果子进程收到退出信号,子进程自行退出。如果父进程收到退出信号,应该先向全部的子进程发送退出信号,然后自己再退出。 演示demo程序 #include <iostream> // 包含输入输出流库,用于输…...

Self-attention与Word2Vec
Self-attention(自注意力)和 Word2Vec 是两种不同的词嵌入技术,用于将单词映射到低维向量空间。它们之间的区别: Word2Vec: Word2Vec 是一种传统的词嵌入(word embedding)方法,旨在为…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
