LeetCode第二题: 两数相加
文章目录
- 题目描述
- 示例
- 解题思路 - 迭代法
- Go语言实现 - 迭代法
- 算法分析
- 解题思路 - 模拟法
- Go语言实现 - 模拟法
- 算法分析
- 解题思路 - 优化模拟法
- 主要方法
- 其他方法的考虑
题目描述
给出两个非空的链表用来表示两个非负的整数。其中,它们各自的位数是按照逆序的方式存储的,并且它们的每个节点只能存储一位数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例
示例 1:
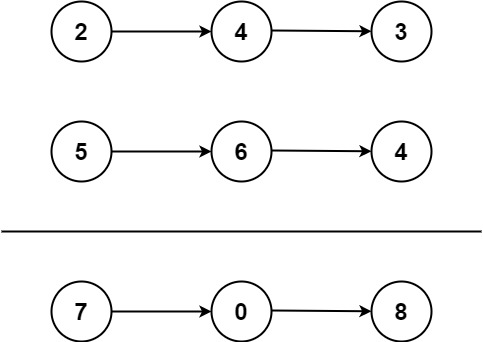
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
解题思路 - 迭代法
我们可以遍历两个链表,模拟数字相加的过程。需要注意的是,如果两个链表的长度不同,我们需要对较短的链表进行特殊处理。另外,如果相加的结果大于等于10,我们需要进行进位处理。
Go语言实现 - 迭代法
下面是使用Go语言实现的迭代法代码:
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {dummyHead := &ListNode{Val: 0}p, q, curr := l1, l2, dummyHeadcarry := 0for p != nil || q != nil {x := 0y := 0if p != nil {x = p.Valp = p.Next}if q != nil {y = q.Valq = q.Next}sum := carry + x + ycarry = sum / 10curr.Next = &ListNode{Val: sum % 10}curr = curr.Next}if carry > 0 {curr.Next = &ListNode{Val: carry}}return dummyHead.Next
}
算法分析
- 时间复杂度: O(max(m, n)),其中 m 和 n 分别为两个链表的长度。
- 空间复杂度: O(max(m, n)),我们需要一个新链表来存储结果。
这个算法的时间复杂度和空间复杂度都是线性的,与较长的链表长度相同。
除了迭代法之外,还可以使用递归法来解决“两数相加”的问题。递归法的基本思想是将问题分解为更小的子问题,即相加两个链表的当前节点,然后递归地处理下一个节点。

解题思路 - 模拟法
通过链表的形式逐位计算两个数的和,同时考虑进位的情况。从两个链表的头节点开始,逐对节点相加,将结果创建为新的链表节点。如果两个链表的长度不一致,则将较短链表的剩余部分视为0进行处理。整个过程中,我们需要维护当前的进位信息。
Go语言实现 - 模拟法
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {head := &ListNode{0, nil} // 创建哑节点作为返回链表的头节点curr := headcarry := 0 // 初始化进位为0for l1 != nil || l2 != nil || carry > 0 {sum := carry // 开始时将进位加入和中if l1 != nil {sum += l1.Val // 加上第一个链表的值l1 = l1.Next // 移动到下一个节点}if l2 != nil {sum += l2.Val // 加上第二个链表的值l2 = l2.Next}carry = sum / 10 // 计算新的进位curr.Next = &ListNode{sum % 10, nil} // 创建新的节点存储和的个位数curr = curr.Next // 移动到新创建的节点}return head.Next // 返回哑节点的下一个节点,即结果链表的头节点
}算法分析
- 时间复杂度: O(max(m,n)),其中 m 和 n 分别是两个链表的长度。我们需要遍历两个链表的最长长度。
- 空间复杂度: O(max(m,n))。新链表的长度最多为 max(m,n) + 1。
解题思路 - 优化模拟法
实际上,上述模拟法已经是相对高效的解法了。在具体实现过程中,进一步的优化空间不大。如果要优化,主要是代码层面的简化和优化,比如简化变量的使用,减少不必要的操作等,但算法本身的时间复杂度和空间复杂度已经达到了最优。
在这个问题中,关键是理解如何逐位相加并处理进位。优化的空间更多的在于代码的可读性和简洁性上,而不是算法复杂度的提升。

对于LeetCode题目2“两数相加”,实际上存在的解决方案主要围绕着迭代和递归两种思路展开。由于题目的特性和限制,解题方法相对固定,主要是如何处理两个链表的逐位相加以及进位处理。
主要方法
- 迭代法:这是最直观的方法,通过遍历两个链表,逐位计算和,并处理进位。迭代法的优点是直观易懂,实现简单,是大多数情况下的首选方法。
- 递归法:递归法利用递归函数来逐位相加,每一层递归处理一位。递归法的优点是代码更为简洁,但对于理解和调试来说可能稍微复杂一些。递归的深度等于链表的长度,因此对于非常长的链表可能会导致栈溢出。
其他方法的考虑
除了这两种方法,实际上没有根本上不同的算法来解决这个特定的问题。其他的所谓“方法”往往是对上述两种方法的变体或优化,例如:
- 优化存储:对于迭代法,可以通过直接在较长的链表上进行修改来节省空间,避免额外的空间分配。但这改变了输入数据,可能并不总是可接受的。
- 并行处理:理论上,如果链表足够长,可以考虑将链表分成几部分并行处理每一部分的加法。然而,这种方法在实践中很少使用,因为它增加了实现的复杂性,而且链表的遍历性质和计算机的内存访问模式使得并行化的效果并不明显。
相关文章:

LeetCode第二题: 两数相加
文章目录 题目描述示例 解题思路 - 迭代法Go语言实现 - 迭代法算法分析 解题思路 - 模拟法Go语言实现 - 模拟法算法分析 解题思路 - 优化模拟法主要方法其他方法的考虑 题目描述 给出两个非空的链表用来表示两个非负的整数。其中,它们各自的位数是按照逆序的方…...

web组态插件
插件演示地址:http://www.byzt.net 关于组态软件,首先要从组态的概念开始说起。 什么是组态 组态(Configure)的概念来自于20世纪70年代中期出现的第一代集散控制系统(Distributed Control System)…...
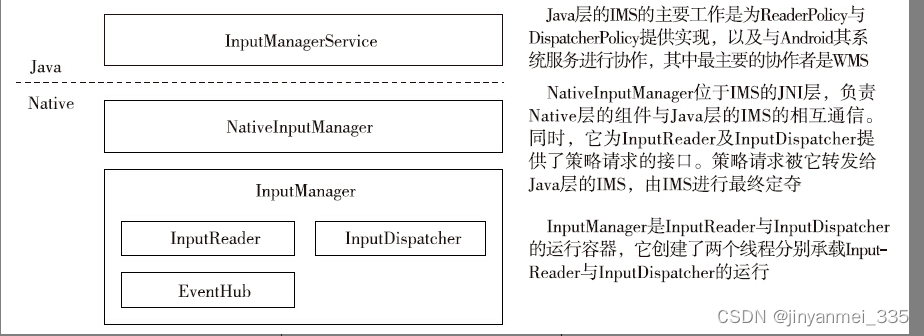
Android14 InputManager-InputManagerService环境的构造
IMS分为Java层与Native层两个部分,其启动过程是从Java部分的初始化开始,进而完成Native部分的初始化。 □创建新的IMS对象。 □调用IMS对象的start()函数完成启动 同其他系统服务一样,IMS在SystemServer中的ServerT…...

搜维尔科技:【周刊】适用于虚拟现实VR中的OptiTrack
适用于 VR 的 OptiTrack 我们通过优化对虚拟现实跟踪最重要的性能指标,打造世界上最准确、最易于使用的广域 VR 跟踪器。其结果是为任何头戴式显示器 (HMD) 或洞穴自动沉浸式环境提供超低延迟、极其流畅的跟踪。 OptiTrack 主动式 OptiTrack 世界领先的跟踪精度和…...
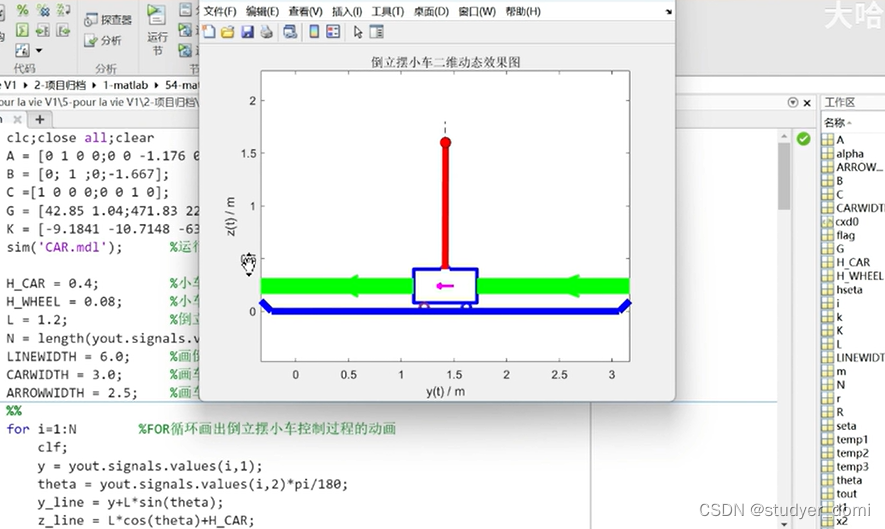
matlab倒立摆小车LQR控制动画
1、内容简介 略 54-可以交流、咨询、答疑 2、内容说明 略 摆杆长度为 L,质量为 m 的单级倒立摆(摆杆的质心在杆的中心处),小车的质量为 M。在水平方向施加控制力 u,相对参考系产生位移为 y。为了简化问题并且保其实质不变,忽…...
【C++】类和对象(2)
目录 1. 初始化列表 2.explicit关键字 3. Static成员 3. 友元 3.1友元函数 3.2友元类 4. 内部类 5.匿名对象 1. 初始化列表 在创建对象时,编译器通过调用构造函数,给对象中各个成员变量一个合适的初始值,但是这个过程并不能称为对对…...
用Python实现创建十二星座数据分析图表
下面小编提供的代码中,您已经将pie.render()注释掉,并使用了pie.render_to_file(十二星座.svg)来将饼状图渲染到一个名为十二星座.svg的文件中。这是一个正确的做法,如果您想在文件中保存图表而不是在浏览器中显示它。 成功创建图表…...
备战蓝桥杯————递归反转单链表的一部分
递归反转单链表已经明白了,递归反转单链表的一部分你知道怎么做吗? 一、反转链表Ⅱ 题目描述 给你单链表的头指针 head 和两个整数 left 和 right ,其中 left < right 。请你反转从位置 left 到位置 right 的链表节点,返回 反…...

rabbitmq知识梳理
一.WorkQueues模型 Work queues,任务模型。简单来说就是让多个消费者绑定到一个队列,共同消费队列中的消息。 当消息处理比较耗时的时候,可能生产消息的速度会远远大于消息的消费速度。长此以往,消息就会堆积越来越多,…...

【数据结构与算法】动态规划法解题20240227
动态规划法 一、什么是动态规划二、动态规划的解题步骤三、509. 斐波那契数1、动规五部曲: 四、70. 爬楼梯1、动规五部曲: 五、746. 使用最小花费爬楼梯1、动规五部曲: 一、什么是动态规划 动态规划,英文:Dynamic Pro…...
备战蓝桥杯—— 双指针技巧巧答链表2
对于单链表相关的问题,双指针技巧是一种非常广泛且有效的解决方法。以下是一些常见问题以及使用双指针技巧解决: 合并两个有序链表: 使用两个指针分别指向两个链表的头部,逐一比较节点的值,将较小的节点链接到结果链表…...

半监督节点分类-graph learning
半监督节点分类相当于在一个图当中,用一部分节点的类别上已知的,有另外一部分节点的类别是未知的,目标是使用有标签的节点来推断没有标签的节点 注意 半监督节点分类属于直推式学习,直推式学习相当于出现新节点后,需要…...
软件文档-运维-开发-管理-资质-评审-招投标-验收
开发文档:这类文档主要用于记录软件的开发过程和细节,包括: 《功能要求》:描述了软件应具备的功能,是软件开发的基础。《投标方案》:向潜在的客户或招标方展示公司的技术和项目实施能力。《需求分析》&…...

猫头虎分享已解决Bug || Vue中的TypeError: Cannot read property ‘name‘ of undefined 错误
博主猫头虎的技术世界 🌟 欢迎来到猫头虎的博客 — 探索技术的无限可能! 专栏链接: 🔗 精选专栏: 《面试题大全》 — 面试准备的宝典!《IDEA开发秘籍》 — 提升你的IDEA技能!《100天精通鸿蒙》 …...

技术应用:使用Spring Boot、MyBatis Plus和Dynamic DataSource实现多数据源
引言 在现代的软件开发中,许多应用程序需要同时访问多个数据库。例如,一个电子商务平台可能需要访问多个数据库来存储用户信息、产品信息和订单信息等。在这种情况下,使用多数据源是一种常见的解决方案,它允许我们在一个应用程序…...
C# Onnx 使用onnxruntime部署实时视频帧插值
目录 介绍 效果 模型信息 项目 代码 下载 C# Onnx 使用onnxruntime部署实时视频帧插值 介绍 github地址:https://github.com/google-research/frame-interpolation FILM: Frame Interpolation for Large Motion, In ECCV 2022. The official Tensorflow 2…...

编程笔记 Golang基础 016 数据类型:数字类型
编程笔记 Golang基础 016 数据类型:数字类型 1. 整数类型(Integer Types)a) 固定长度整数:b) 变长整数: 2. 浮点数类型(Floating-Point Types)3. 复数类型(Complex Number Types&…...
一周学会Django5 Python Web开发-会话管理(CookiesSession)
锋哥原创的Python Web开发 Django5视频教程: 2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 Django5 Python web开发 视频教程(无废话版) 玩命更新中~共计26条视频,包括:2024版 Django5 Python we…...

QT之QString.arg输出固定位数
问题描述 我需要用QString输出一个固定位数的数字字符串。起初我的代码是这样: int img_num 1 auto new_name QString("%1.png").arg((int)img_num, 3, 10, 0); //最后一个参数用u0也是一样的 qDebug() << "new_name:" << new…...

Linux下各种压缩包的压缩与解压
tar 归档,不压缩,常见后缀 .tar # 将文件夹归档成为一个包 tar cf rootfs.tar rootfs # 将归档包还原为文件夹 tar xf rootfs.tar # 将归档包还原到路径 a/b/c tar xf rootfs.tar -C a/b/cgzip压缩, 常见后缀 .tar.gz .tgz # 压缩 tar czf …...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...
