KNN学习报告
- 原理
KNN算法就是在其表征空间中,求K个最邻近的点。根据已知的这几个点对其进行分类。如果其特征参数只有一个,那么就是一维空间。如果其特征参数只有两个,那么就是二维空间。如果其特征参数只有三个,那么就是三维空间。如果其特征参数大于三个,那么就是N维抽象空间。在表征空间中,不同点的距离采用如下所示的欧几里得方法进行计算。
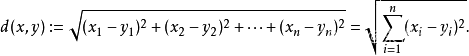
K值根据经验选择最合适的参数,太小不够稳健,太大的话容易受样本不足制约。也可以根据交叉验证的方法,确定最优的K值。一般取5~10之间的一个数。
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 看下面这幅图:

KNN的算法过程是是这样的: 从上图中我们可以看到,图中的数据集是良好的数据,即都打好了label,一类是蓝色的正方形,一类是红色的三角形,那个绿色的圆形是我们待分类的数据。 如果K=3,那么离绿色点最近的有2个红色三角形和1个蓝色的正方形,这3个点投票,于是绿色的这个待分类点属于红色的三角形 如果K=5,那么离绿色点最近的有2个红色三角形和3个蓝色的正方形,这5个点投票,于是绿色的这个待分类点属于蓝色的正方形 我们可以看到,KNN本质是基于一种数据统计的方法!其实很多机器学习算法也是基于数据统计的。 KNN是一种memory-based learning,也叫instance-based learning,属于lazy learning。即它没有明显的前期训练过程,而是程序开始运行时,把数据集加载到内存后,不需要进行训练,就可以开始分类了。 具体是每次来一个未知的样本点,就在附近找K个最近的点进行投票。
- 三个距离算法
欧氏距离:是一个通常采用的距离定义,指在n维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离),在二维和n维空间中的欧氏距离就是两点之间的实际距离。
def euclideanDistance(x1, x2):
# 欧氏距离
tempDistance = 0
for i in range(x1.shape[0]):
difference = x1[i] - x2[i]
tempDistance += difference * difference
tempDistance = tempDistance ** 0.5
return tempDistance
马氏距离:马氏距离(Mahalanobis Distance)是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。其中Σ是多维随机变量的协方差矩阵,μ为样本均值,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离。

def mashi_distance(x,y):
X = numpy.vstack([x, y])
XT = X.T
# 方法一:根据公式求解
S = numpy.cov(X) # 两个维度之间协方差矩阵
SI = numpy.linalg.inv(S) # 协方差矩阵的逆矩阵
# 马氏距离计算两个样本之间的距离
n = XT.shape[0]
d1 = 0
for i in range(0, n):
for j in range(i + 1, n):
delta = XT[i] - XT[j]
d = numpy.sqrt(numpy.dot(numpy.dot(delta, SI), delta.T))
d1 = d1 + d
return d1
曼哈顿距离:种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。
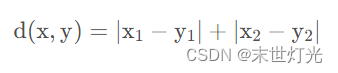
def ManhattanDistance(x, y):
x = numpy.array(x)
y = numpy.array(y)
return numpy.sum(numpy.abs(x-y))
- 三个数据集
Iris数据集:Iris Data Set(鸢尾属植物数据集)是我现在接触到的历史最悠久的数据集,它首次出现在著名的英国统计学家和生物学家Ronald Fisher 1936年的论文《The use of multiple measurements in taxonomic problems》中,被用来介绍线性判别式分析。在这个数据集中,包括了三类不同的鸢尾属植物:Iris Setosa,Iris Versicolour,Iris Virginica。每类收集了50个样本,因此这个数据集一共包含了150个样本。
该数据集测量了所有150个样本的4个特征,分别是:sepal length(花萼长度);sepal width(花萼宽度);petal length(花瓣长度);petal width(花瓣宽度)以上四个特征的单位都是厘米(cm)。通常使用mm表示样本量的大小,nn表示每个样本所具有的特征数。因此在该数据集中,m=150,n=4m=150,n=4。
# iris数据集
tempDataset = sklearn.datasets.load_iris()
葡萄酒分类数据集:Wine葡萄酒数据集是来自UCI上面的公开数据集,这些数据是对意大利同一地区种植的葡萄酒进行化学分析的结果,这些葡萄酒来自三个不同的品种。该分析确定了三种葡萄酒中每种葡萄酒中含有的13种成分的数量。从UCI数据库中得到的这个wine数据记录的是在意大利某一地区同一区域上三种不同品种的葡萄酒的化学成分分析。数据里含有178个样本分别属于三个类别,这些类别已经给出。每个样本含有13个特征分量(化学成分),分析确定了13种成分的数量,然后对其余葡萄酒进行分析发现该葡萄酒的分类。
在wine数据集中,这些数据包括了三种酒中13种不同成分的数量。文件中,每行代表一种酒的样本,共有178个样本;一共有14列,其中,第一个属性是类标识符,分别是1/2/3来表示,代表葡萄酒的三个分类。后面的13列为每个样本的对应属性的样本值。剩余的13个属性是,酒精、苹果酸、灰、灰分的碱度、镁、总酚、黄酮类化合物、非黄烷类酚类、原花色素、颜色强度、色调、稀释葡萄酒的OD280/OD315、脯氨酸。其中第1类有59个样本,第2类有71个样本,第3类有48个样本。
# 葡萄酒分类数据集
tempDataset = sklearn.datasets.load_wine()
手写分类数据集:在这个数据集中,包含1797张8*8灰度的图像。每个数据点都是一个数字,共有10种类别(数字0~9)。
# 手写数字分类数据集
tempDataset = sklearn.datasets.load_digits()
- 实验对比

- 结论
本次实验内容包括三种数据集分别对三种距离测量算法进行knn预测分类,同一种数据集在不同距离测量算法下计算精度也不尽相同。其中,手写数字数据集在使用马氏距离过程中计算量过大,不适宜使用马氏距离计算。
import sklearn.datasets, sklearn.neighbors, sklearn.model_selection
import numpy
from sklearn import metricsdef sklearnKnnTest():#Step 1. Load the dataset# iris数据集#tempDataset = sklearn.datasets.load_iris()# 葡萄酒分类数据集#tempDataset = sklearn.datasets.load_wine()# 手写数字分类数据集tempDataset = sklearn.datasets.load_digits()x = tempDataset.datay = tempDataset.target#print("x = ", x)#print("y = ", y)#Step 2. Split the dataX1, X2, Y1, Y2 = sklearn.model_selection.train_test_split(x, y, test_size = 0.2)print("X1 = ", X1)print("Y1 = ", Y1)print("X2 = ", X2)print("Y2 = ", Y2)#Step 3. Indicate the training set.tempClassifier = sklearn.neighbors.KNeighborsClassifier(n_neighbors = 5)tempClassifier.fit(X1, Y1)#Step 4. Test.tempScore = tempClassifier.score(X2, Y2)print("The score is: ", tempScore)def euclideanDistance(x1, x2):# 欧氏距离tempDistance = 0for i in range(x1.shape[0]):difference = x1[i] - x2[i]tempDistance += difference * differencetempDistance = tempDistance ** 0.5return tempDistance
# 马氏距离
def mashi_distance(x,y):X = numpy.vstack([x, y])XT = X.T# 方法一:根据公式求解S = numpy.cov(X) # 两个维度之间协方差矩阵SI = numpy.linalg.inv(S) # 协方差矩阵的逆矩阵# 马氏距离计算两个样本之间的距离n = XT.shape[0]d1 = 0for i in range(0, n):for j in range(i + 1, n):delta = XT[i] - XT[j]d = numpy.sqrt(numpy.dot(numpy.dot(delta, SI), delta.T))d1 = d1 + dreturn d1
# 曼哈顿距离
def ManhattanDistance(x, y):x = numpy.array(x)y = numpy.array(y)return numpy.sum(numpy.abs(x-y))def mfKnnTest(k = 3):#Step 1. Load the dataset# iris数据集#tempDataset = sklearn.datasets.load_iris()# 葡萄酒分类数据集#tempDataset = sklearn.datasets.load_wine()# 手写数字分类数据集tempDataset = sklearn.datasets.load_digits()x = tempDataset.datay = tempDataset.target#print("x = ", x)#print("y = ", y)#Step 2. Split the dataX1, X2, Y1, Y2 = sklearn.model_selection.train_test_split(x, y, test_size = 0.2)# print("X1 = ", X1)# print("Y1 = ", Y1)# print("X2 = ", X2)# print("Y2 = ", Y2)#Step 3. ClassifytempPredicts = numpy.zeros(Y2.shape[0])for i in range(X2.shape[0]):#Step 3.1 Find k neigbhors#InitializetempNeighbors = numpy.zeros(k + 2)tempDistances = numpy.zeros(k + 2)for j in range(k + 2):tempDistances[j] = 1000tempDistances[0] = -1for j in range(X1.shape[0]):# 欧氏距离#tempDistance = euclideanDistance(X2[i], X1[j])# 马氏距离tempDistance = mashi_distance(X2[i], X1[j])# 曼哈顿距离#tempDistance = ManhattanDistance(X2[i], X1[j])tempIndex = kwhile True:if tempDistance < tempDistances[tempIndex]:#Move forward#print("tempDistance = {} and tempDistances[{}] = {}".format(tempDistance, tempIndex, tempDistances[tempIndex]))tempNeighbors[tempIndex + 1] = tempNeighbors[tempIndex]tempDistances[tempIndex + 1] = tempDistances[tempIndex]tempIndex -= 1else:#Insert heretempNeighbors[tempIndex + 1] = jtempDistances[tempIndex + 1] = tempDistance#print("Insert to {}.".format(tempIndex))break#print("Classifying ", X2[i])#print("tempNeighbors = ", tempNeighbors)#Step 3.2 Vote#Step 2.2 Vote for the classtempLabels = []for j in range(k):tempIndex = int(tempNeighbors[j + 1])tempLabels.append(int(Y1[tempIndex]))tempCounts = []for label in tempLabels:#print("count = ", tempLabels.count(label))tempCounts.append(int(tempLabels.count(label)))tempPredicts[i] = tempLabels[numpy.argmax(tempCounts)]print("The predictions are: ", tempPredicts)print("The true labels are: ", Y2)print('The accuracy of the KNN is: {:.3f}'.format(metrics.accuracy_score(tempPredicts, Y2)))return metrics.accuracy_score(tempPredicts, Y2)def main():#sklearnKnnTest()#print("Life is short, so I study python.")list = []for i in range(6):list.append(mfKnnTest())print(list)main()
相关文章:

KNN学习报告
原理 KNN算法就是在其表征空间中,求K个最邻近的点。根据已知的这几个点对其进行分类。如果其特征参数只有一个,那么就是一维空间。如果其特征参数只有两个,那么就是二维空间。如果其特征参数只有三个,那么就是三维空间。如果其特征…...
Java奠基】方法的讲解与使用
目录 方法概述 方法的定义与调用 方法的重载 方法的值传递 方法概述 方法是程序中最小的执行单元,在实际开发中会将重复的具有独立功能的代码抽取到方法中,这样可以提高代码的复用性和可维护性。 方法的定义与调用 在Java中定义方法的格式都是相同…...

字符串hash
K - 子串翻转回文串2020ccpc河南省赛字符串哈希:将字符串变成x进制数对公式的理解:举个十进制数的例子:123456h[1]1;h[2]1*10212;h[3]12*103123;h[4]123*1041234;.........h[i]h[i-1]*xa[i];h[i]代表的恰巧是整个数的前缀用p[i]表…...

试题 算法训练 转圈游戏
问题描述 n个小伙伴(编号从0到n-1)围坐一圈玩游戏。按照顺时针方向给n个位置编号,从0到n-1。 最初,第0号小伙伴在第0号位置,第1号小伙伴在第 1 号位置,……,依此类推。 游戏规则如下&am…...

【uni-app教程】九、运行环境判断与跨端兼容
(1)开发环境和生产环境 uni-app 可通过 process.env.NODE_ENV 判断当前环境是开发环境还是生产环境,一般用于连接测试服务器或生产服务器的动态切换。 在HBuilderX 中,点击「运行」编译出来的代码是开发环境,点击「发行…...

扩展WSL2虚拟硬盘的大小
扩展WSL2虚拟硬盘的大小 1、在 Windows PowerShell 中终止所有 WSL 实例 wsl --shutdown2、查看 WSL 实例运行状态,确认关闭,并记住发行版的名称 wsl -l -v如果没有更改移动过发行版安装包位置,那么可以通过以下方法查找到发行版的安装包位…...

Win系统蓝牙设备频繁卡顿/断连 - 解决方案
Win系统蓝牙设备频繁卡顿/断连 - 解决方案前言常见网卡Intel无线网卡(推荐)Realtek无线网卡总结查看本机网卡解决方案更新驱动更换网卡(推荐)前言 无线网卡有2个模块,一个是WiFi,一个是蓝牙,因…...
Git学习入门(2)- 基本命令操作总结
个人博客:我的个人博客,各位大佬来玩1 创建 git仓库1.1 从现有工作目录中初始化新仓库需要到你需要用git管理的项目中输入以下命令:git init便会创建一个空的git项目,并且当前目录下会出现一个名为 .git 的目录, Git 需…...

SPringCloud:Nacos快速入门及相关属性配置
目录 一、Nacos快速入门 1、在父工程中添加spring-cloud-alilbaba的管理依赖 2、如果有使用eureka依赖,将其注释 3、添加nacos的客户端依赖 4、修改yml文件,注释eureka配置 5、启动测试 二、Nacos相关属性配置 1、Nacos服务分级存储 2、根据集群…...

医疗器械之模糊算法(嵌入式部分)
模糊控制 所谓模糊控制,就是对难以用已有规律描述的复杂系统,采用自然语言(如大,中,小)加以描述,借助定性的,不精确的以及模糊的条件语句来表达,模糊控制是一种基于语言的…...
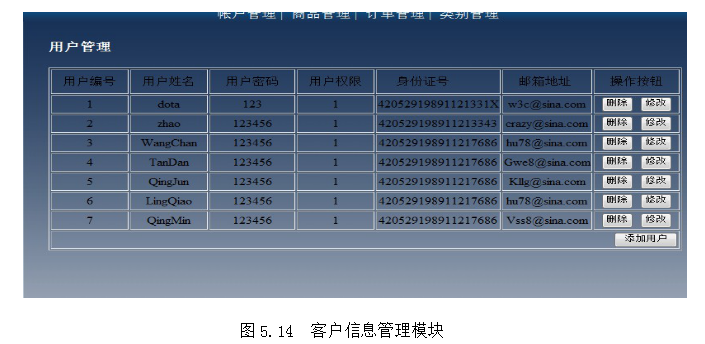
网上销售笔记本系统
技术:Java、JSP等摘要:本文讲述了基于B/S模式的笔记本电脑在线销售系统的设计与实现。所谓的笔记本电脑在线销售系统是通过网站推广互联企业的笔记本电脑和技术服务,并使客户随时可以了解企业和企业的产品,为客户提供在线服务和订…...
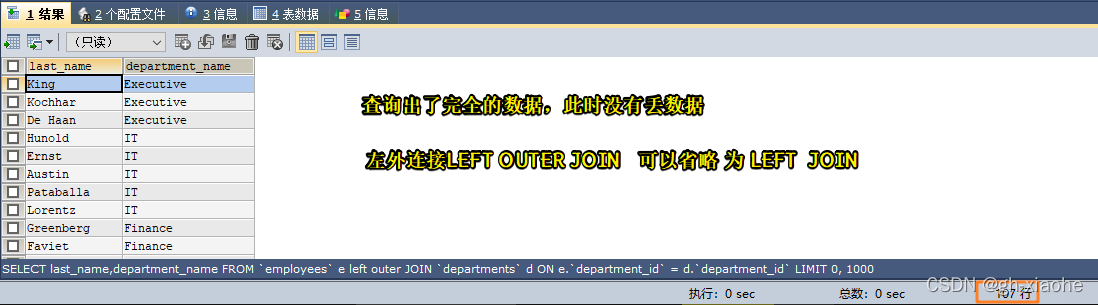
MySQL基础查询操作
文章目录🚏 Select语句🚀 一、SQL底层执行原理🚬 (一)、查询的结构🚬 (二)、SQL语句的执行过程🚭 1、WHERE 为什么不包含聚合函数的过滤条件?(面试…...

English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三
English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ʌ]&…...
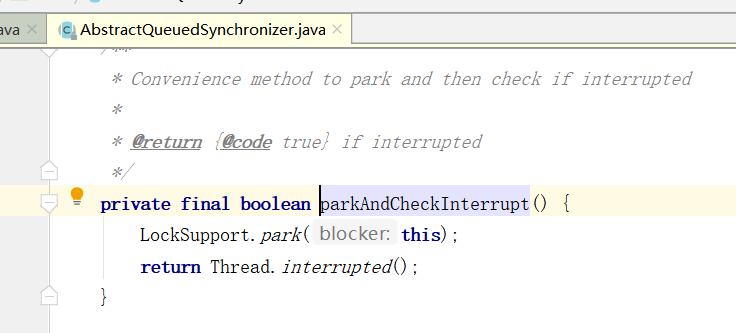
Condition 源码解读
一、Condition 在并发情况下进行线程间的协调,如果是使用的 synchronized 锁,我们可以使用 wait/notify 进行唤醒,如果是使用的 Lock 锁的方式,则可以使用 Condition 进行针对性的阻塞和唤醒,相较于 wait/notify 使用…...
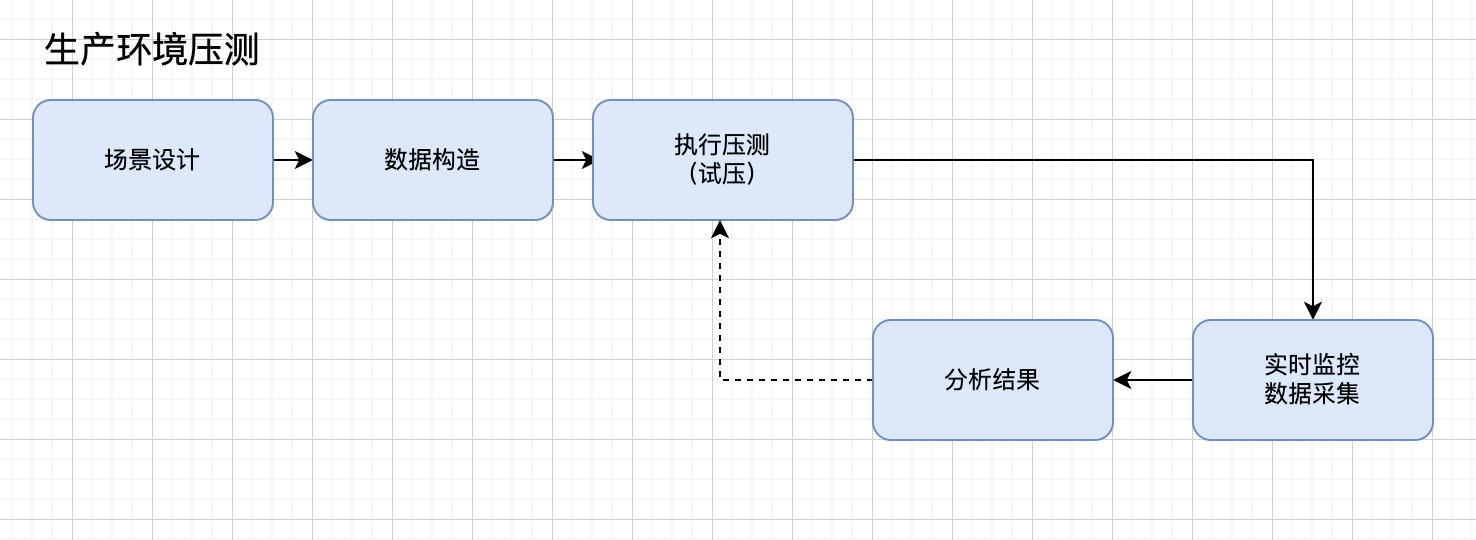
看完这篇入门性能测试
大家好,我是洋子。最近组内在进行服务端高并发接口的性能压测工作,起因是2023年2月2日,针对胡某宇事件进行新闻发布会直播,几十万人同时进入某媒体直播间,造成流量激增 从监控上可以看出,QPS到达某峰值后&…...

推导部分和——带权并查集
题解: 带权并查集 引言: 带权并查集是一种进阶的并查集,通常,结点i的权值等于结点i到根节点的距离,对于带权并查集,有两种操作需要掌握——Merge与Find,涉及到路径压缩与维护权值等技巧。 带…...
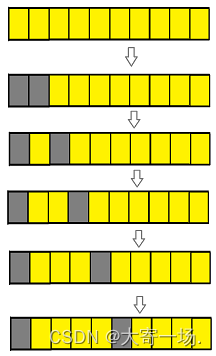
费解的开关/翻硬币
🌱博客主页:大寄一场. 🌱系列专栏: 算法 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 题目:费解的开关 你玩过“拉灯”游戏吗? 25盏灯排成一个 55 的方形。 每一个灯都有一个开关&…...
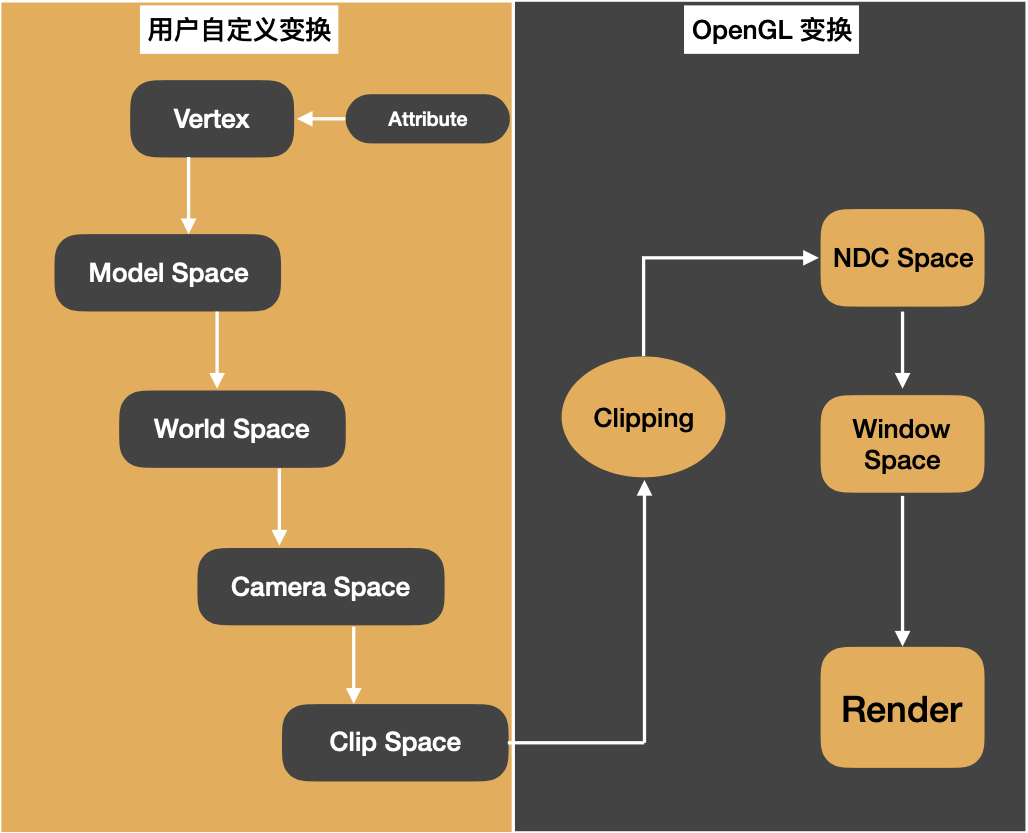
OpenGL中的坐标系
1、2D笛卡尔坐标系2D笛卡尔坐标系跟我们高中的时候学习的坐标系一样,是由x、y决定的。2、3D笛卡尔坐标系3D笛卡尔坐标系坐标由x、y、z决定,满足右手定则。3、视口glViewport(GLint x,GLint y,GLsizei width,GLsizei height)窗口和视口大小可以相同&#…...

Spring——Spring介绍和IOC相关概念
Spring是以Spring Framework为核心,其余的例如Spring MVC, Spring Cloud,Spring Data,Spring Security SpringBoot的基础都是Spring Framework。 Spring Boot可以在简化开发的基础上加速开发。 Spring Cloud分布式开发 Spring有…...

A+B Problem
AB Problem 题目描述 输入两个整数 a,ba, ba,b,输出它们的和(∣a∣,∣b∣≤109|a|,|b| \le {10}^9∣a∣,∣b∣≤109)。 注意 Pascal 使用 integer 会爆掉哦!有负数哦!C/C 的 main 函数必须是 int 类型,…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
