工具篇(五)炫酷排版,尽在LaTeX:让你的文档飞升吧!
作者的话
作为一个文本排版工具,latex一直以来都备受科研工作者、学生和出版社的青睐。但是对于初学者来说,latex的学习曲线可能会有些陡峭。因此,我写这篇博客旨在为初学者提供一个简单易懂的latex教程,让大家能够快速入门并掌握基本的排版技巧。希望这篇博客能够帮助到大家,如果你有任何问题或者建议,欢迎在评论区留言,同时也希望大家能够三连支持,谢谢!
一、latex源文件基本结构
LaTeX 源文件的基本结构包括以下几个部分:
1.文档类声明:通过指定文档类来定义文档的基本格式和样式。例如,声明文档类为 article:
\documentclass{article}2.导言区:在导言区中可以设置文档的全局属性,引用宏包,定义命令和环境等。例如,导入常用的宏包和自定义命令:
\usepackage{graphicx}
\newcommand{\mycommand}{Some text}
3.正文部分:正文部分是文档的主体内容,包括标题、段落、列表、图片、表格等。例如,插入一张图片和一个表格:
% 文档正文
\begin{document}
% 标题、作者等信息
\title{标题}
\author{作者}
\date{日期}
\maketitle
% 目录
\tableofcontents
% 正文
\section{章节标题}
\subsection{小节标题}
正文内容
% 结束正文
\end{document}4.结束语句:在文档的末尾需要添加结束语句以告诉 LaTeX 编译器文档已经结束。例如:
\end{document}二、数学公式初步
2.1行内公式
LaTeX 中有多种方法可以排版行内公式。以下是其中一些常用的方法:
使用一对美元符号 $ 将公式包裹起来,例如: $y = mx + b$。这是最常用的方法。
使用一对小括号 () 将公式包裹起来,例如: \(y = mx + b\)。
使用一对斜杠 \[ \] 将公式包裹起来,例如: \[y = mx + b\]。这种方式可以用于排版独立的行间公式。
2.2上标和下标
在 LaTeX 中,上标和下标是常用的数学符号,用于表示某些变量或常数的指数或下标。下面详细介绍 LaTeX 中的上标和下标的用法:
上标
使用 ^ 符号来表示上标。例如,x^2 表示 $x$ 的平方。
如果要上标的内容是多个字符,可以用一对花括号 {} 将其括起来。例如,a^{n-1} 表示 $a$ 的 $n-1$ 次方。
上标的内容可以是任意的数学表达式,包括分数、根式等。例如,\frac{1}{2}^2 表示 $\frac{1}{2}$ 的平方。
如果需要添加多个上标,可以使用一对花括号 {} 来区分不同的上标。例如,x^{2n}_{k+1} 表示 $x$ 的第 $k+1$ 个下标上面的 $2n$ 次方。
下标
使用 _ 符号来表示下标。例如,x_1 表示 $x$ 的第一个下标。
如果需要添加多个下标,可以使用一对花括号 {} 来区分不同的下标。例如,a_{i,j,k} 表示 $a$ 的第 $i,j,k$ 个下标。
下标的内容可以是任意的数学表达式,包括分数、根式等。例如,a_{\frac{1}{2}} 表示 $a$ 的下标是 $\frac{1}{2}$。
如果要下标的内容是多个字符,可以用一对花括号 {} 将其括起来。例如,x_{n-1} 表示 $x$ 的第 $n-1$ 个下标。
注意:
如果上标或下标的内容较长,可以使用 \mathrm{} 或 \text{} 命令来保证其正常显示。例如,x_{\mathrm{max}} 表示 $x$ 的下标是“max”。
在使用多个上标或下标时,需要使用一对花括号 {} 来区分不同的上标或下标,否则会出现错误。
如果需要同时使用上标和下标,可以使用一对花括号 {} 来区分不同的上标和下标。例如,x^{2n}_{k+1} 表示 $x$ 的第 $k+1$ 个下标上面的 $2n$ 次方
2.3希腊字母
在 LaTeX 中,可以使用希腊字母来表示各种数学符号和变量。下面列出了 LaTeX 中常用的希腊字母及其对应的命令:
这些命令可以在数学环境中使用,例如在 $...$ 或 \[...\] 中。例如,输入 \alpha+\beta=\gamma 将会得到 。
2.4数学函数
下面是常见数学函数的表格及其LaTeX代码和含义:
| 函数 | LaTeX | 含义 |
|---|---|---|
| 平方根 | ‘\sqrt{x}’ | |
| 立方根 | ‘\sqrt[3]{x}’ | |
| 向上取整 | ‘\lceil x \rceil’ | |
| 向下取整 | '\lfloor x \rfloor' | |
| 绝对值 | ‘\left| x \right|’ | |
| 自然对数 | ‘\ln x’ | |
| 以10为底的对数 | '\log x' | |
| 以a为底的对数 | '\log_a x' | |
| 正弦函数 | '\sin x' | |
| 余弦函数 | '\cos x' | |
| 正切函数 | '\tan x' | |
| 余切函数 | '\cot x' | |
| 正割函数 | '\sec x' | |
| 余割函数 | '\csc x' | |
| 反正弦函数 | '\arcsin x' | |
| 反余弦函数 | '\arccos x' | |
| 反正切函数 | ' |
这些函数可以在数学环境中使用,需要使用$...$或\[...\]进行数学模式。例如,\sin x将生成正弦函数的符号。
2.5分式
在LaTeX中,可以使用\frac{numerator}{denominator}命令来创建分式。其中,numerator表示分子,denominator表示分母。例如,\frac{1}{2}可以生成一个的分数。
2.6行间公式
LaTeX的行间公式使用$$ equation $$或\begin{equation} equation \end{equation}命令创建,一般独占一行。公式的大小、字体、对齐等样式与周围的文本不同。在行间公式中,可以使用各种数学符号和命令,例如上下标、分式、根号、求和符号等等。公式中的上下标、根号等符号比行内公式中更大,以便更清晰地显示公式内容。
2.7求和函数和求积函数
LaTeX中,求和公式和求积公式可以用\sum和\prod命令创建。
求和公式:
格式:\sum_{下标起始值}^{下标结束值} 被求和的表达式
示例:$$ \sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{\pi^2}{6} $$
效果:
求积公式:
格式:\prod_{下标起始值}^{下标结束值} 被求积的表达式
示例:$$ \prod_{n=1}^{\infty} \left(1 + \frac{1}{n}\right)^n = e^\frac{1}{2} $$
效果:
在上述示例中,下标起始值和下标结束值可以是任何数学表达式,例如常数、变量、函数等。求和公式和求积公式中的表达式可以包括各种数学符号和函数。
2.8矩阵
在LaTeX中,矩阵可以使用matrix环境来创建。下面是一个示例:
在矩阵环境,用&分隔列,用\\分隔行
\begin{matrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{matrix}该代码将生成一个 的矩阵,如下所示:
如果你想为矩阵添加括号,请使用bmatrix(方括号)、pmatrix(圆括号)、Bmatrix(大括号)、vmatrix(单竖线)或Vmatrix(双竖线)环境例如
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix}
生成
在矩阵中可以使用各种数学符号、上下标、分数等等。例如,下面的代码生成了一个含有上下标和分数的矩阵:
\begin{bmatrix}
a_{11} & \frac{a_{12}}{2} & a_{13} \\
a_{21} & a_{22}^{2} & a_{23} \\
a_{31}^{3} & a_{32} & a_{33}
\end{bmatrix}生成
矩阵中还可以使用省略号来表示一些元素的省略,其中 \dots 表示水平省略号,\vdots 表示垂直省略号,\ddots 表示对角省略号。
\begin{pmatrix}
1 & 2 & \dots & n \\
2 & 5 & \dots & 2n \\
\vdots & \vdots & \ddots & \vdots \\
n & 2n & \dots & n^2 \\
\end{pmatrix}生成:
可用\times排版乘号


三角矩阵
在 LaTeX 中,三角矩阵可以通过 amsmath 宏包中的 matrix 环境和 bmatrix、pmatrix、vmatrix 等环境来创建。以 bmatrix 环境为例,示例如下:
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
0 & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn}
\end{bmatrix}
生成
2.9多行数学公式
在 LaTeX 中,我们可以使用多种方式来排版多行数学公式。下面是几种常见的方式:
1.使用 equation 环境
equation 环境适用于单个数学公式,但是也可以用来排版多行公式。在 equation 环境中,使用 \nonumber 来标记不需要编号的行。示例如下
\begin{equation}
\begin{aligned}
f(x) &= (x + 1)^2 \\
&= x^2 + 2x + 1. \nonumber
\end{aligned}
\end{equation}生成
2.使用 align 环境
align 环境用于排版多行公式,可以使用 & 符号来对齐等号。示例如下:
\begin{align}
f(x) &= (x + 1)^2 \\
&= x^2 + 2x + 1.
\end{align}
生成
3.使用 split 环境
split 环境适用于将一个数学公式拆分成多行,可以与 equation、align、gather 等环境配合使用。示例如下:
\begin{equation}
\begin{split}
f(x) &= (x + 1)^2 \\
&= x^2 + 2x + 1.
\end{split}
\end{equation}
生成
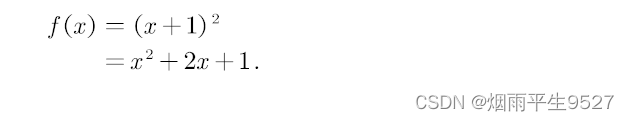
2.10符号
1.比较符号:输入 =、<、>、\leq、\geq、\neq 表示等于、小于、大于、小于等于、大于等于、不等于,例如 x=y 表示 $x=y$。
2.运算符号:输入 \pm、\times、\div、\cdot、\sqrt 表示加减、乘、除、点乘、平方根等。3.微分符号:一阶导数:$f'(x) = \frac{\mathrm{d}f(x)}{\mathrm{d}x}$
二阶导数:$f''(x) = \frac{\mathrm{d}^2f(x)}{\mathrm{d}x^2}$
偏导数:$\frac{\partial f(x,y)}{\partial x}$
注意,在微分符号前后需要使用空格,以使其与其他数学符号分隔开来。
4.积分符号:Latex中积分符号使用\int命令,下面是一些示例:
普通积分:$\int f(x)dx$
带限的积分:$\int_{a}^{b} f(x)dx$
多重积分:$\iint f(x,y) dxdy$
$\iiint f(x,y,z) dxdydz$带限的多重积分:$\iiint_{V} f(x,y,z) dxdydz$
累次积分:$\int \int f(x,y) dxdy$
5.向量符号:向量通常使用加粗的字母表示,例如 $\mathbf{v}$ 表示向量 $v$。可以使用 \mathbf 命令来生成加粗的字母。另外,有时也会使用箭头表示向量,例如 $\vec{v}$ 表示向量 $v$。可以使用 \vec 命令来生成带箭头的字母。
使用加粗的字母表示向量:$\mathbf{v} = (v_1, v_2, \dots, v_n)$。
使用箭头表示向量:$\vec{v} = (v_1, v_2, \dots, v_n)$。
表示向量的范数:$\lVert \mathbf{v} \rVert = \sqrt{\sum_{i=1}^n v_i^2}$。
表示向量的点积:$\mathbf{u} \cdot \mathbf{v} = \sum_{i=1}^n u_i v_i$。
其中,范数可以使用 \lVert 和 \rVert 命令来生成双竖线,点积可以使用 \cdot 命令来生成点乘号。
2.11行列式
行列式是数学中一种特殊的运算,可以表示为一个方形矩阵中各行各列元素的排列组合。在 LaTeX 中,可以使用“\begin{vmatrix} ... \end{vmatrix}”或“\begin{Vmatrix} ... \end{Vmatrix}”命令来表示行列式,其中 vmatrix 生成单竖线的行列式,而 Vmatrix 生成双竖线的行列式。在“\begin{vmatrix}”或“\begin{Vmatrix}”命令的两个大括号中,可以输入矩阵的元素。
例如,一个 3x3 的行列式可以表示为:
\begin{vmatrix}
a & b & c \\
d & e & f \\
g & h & i
\end{vmatrix}生成
行列式的值可以使用“\left| ... \right|”命令来表示,其中“\left|”表示左竖线,而“\right|”表示右竖线。例如,可以使用“\left| \begin{matrix} ... \end{matrix} \right|”命令来表示一个矩阵的行列式值,其中“\begin{matrix} ... \end{matrix}”命令表示一个矩阵,矩阵的元素也可以通过“&”和“\”符号来表示。
对于上述的 3x3 行列式,可以使用以下命令来表示其行列式值:
\left|
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i
\end{matrix}
\right|生成
行列式的值可以使用“det”命令来表示。例如,可以使用“\det(A)”命令来表示一个矩阵 A 的行列式值。
2.12极限
在 LaTeX 中表示极限可以使用\lim命令,例如:
\lim_{x\to a} f(x)这个命令将会生成一个极限符号,并在符号的下方放置一个下标,表示 $x$ 趋向于 $a$。在下标的右侧放置被取极限的函数 $f(x)$。
类似于分式,极限符号可以在文本或公式环境中使用,但通常会在数学环境中使用。如果您希望极限符号与其他符号垂直对齐,可以使用\limits命令:
\lim\limits_{x\to a} f(x)在这个命令中,\limits命令告诉 LaTeX 将下标和上标放置在极限符号的上方和下方,而不是侧面。
此外,如果需要在极限符号下方和上方添加文本,可以使用\underset和\overset命令:
\lim_{\underset{x\to a}{x > 0}} f(x)在这个命令中,\underset命令将下方的文本放在极限符号下方,而不是默认的位置。同样,\overset命令可以将文本放在极限符号上方。
相关文章:
工具篇(五)炫酷排版,尽在LaTeX:让你的文档飞升吧!
作者的话 作为一个文本排版工具,latex一直以来都备受科研工作者、学生和出版社的青睐。但是对于初学者来说,latex的学习曲线可能会有些陡峭。因此,我写这篇博客旨在为初学者提供一个简单易懂的latex教程,让大家能够快速入门并掌握…...
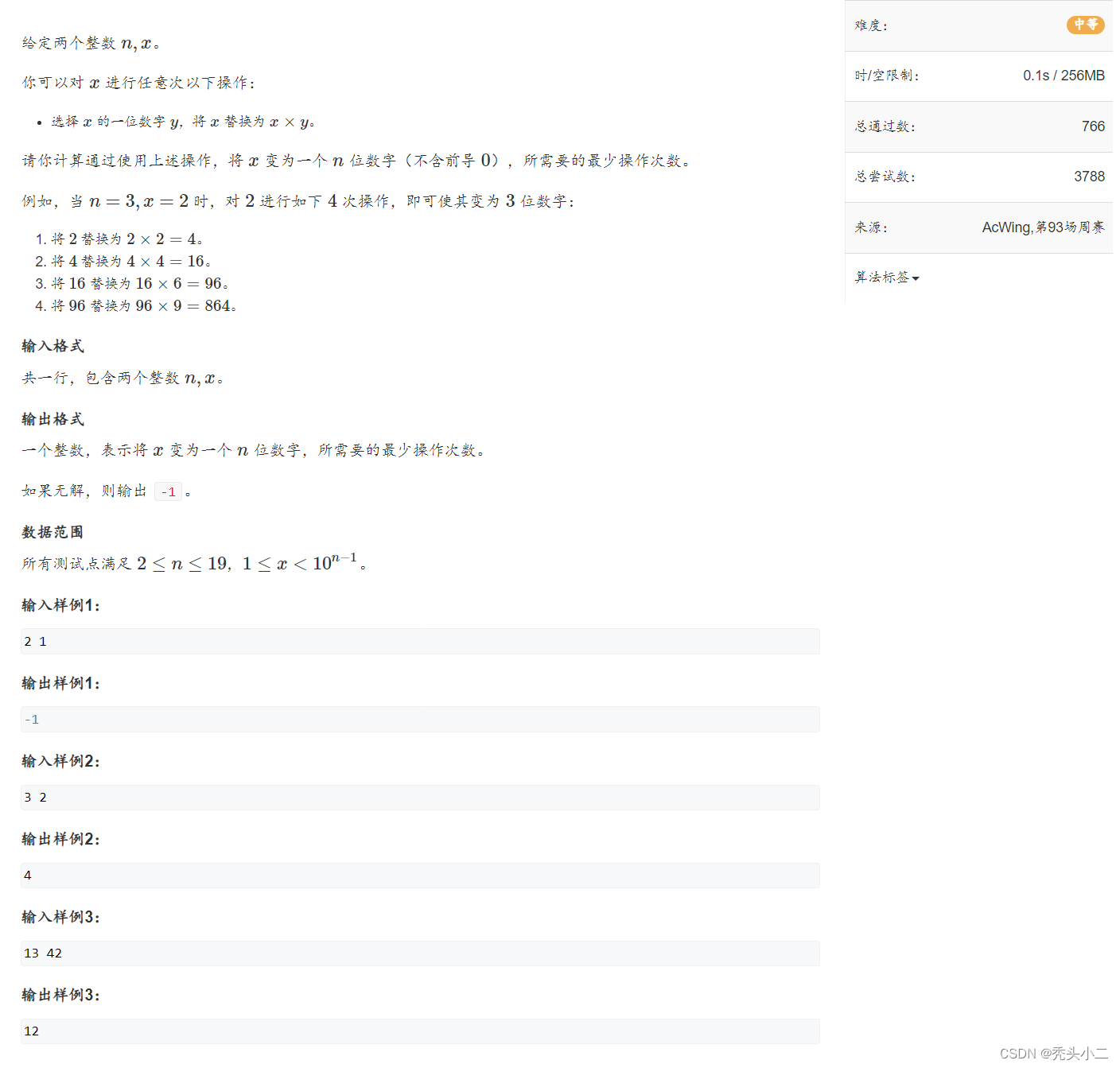
【蓝桥杯PythonB组备赛】【Acwing周赛】第93场 4867. 整除数 4868. 数字替换 python解
目录 A AcWing 4867. 整除数 1.题目描述 2.思路分析 3.代码实现 B AcWing 4868. 数字替换 1.题目描述 2.思路分析 3.代码实现 A AcWing 4867. 整除数 1.题目描述 2.思路分析 为什么不能直接暴力? 数据:1 ≤ n, k ≤ 10 ** 9 1s内最多…...

KNN学习报告
原理 KNN算法就是在其表征空间中,求K个最邻近的点。根据已知的这几个点对其进行分类。如果其特征参数只有一个,那么就是一维空间。如果其特征参数只有两个,那么就是二维空间。如果其特征参数只有三个,那么就是三维空间。如果其特征…...
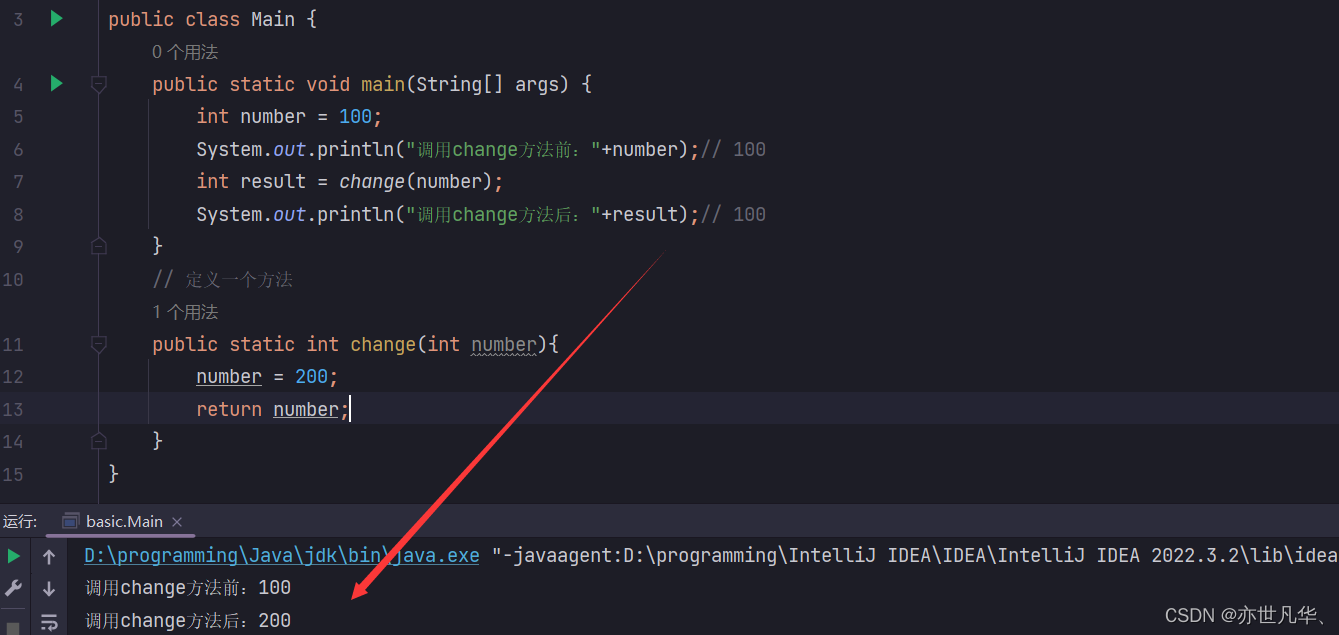
Java奠基】方法的讲解与使用
目录 方法概述 方法的定义与调用 方法的重载 方法的值传递 方法概述 方法是程序中最小的执行单元,在实际开发中会将重复的具有独立功能的代码抽取到方法中,这样可以提高代码的复用性和可维护性。 方法的定义与调用 在Java中定义方法的格式都是相同…...

字符串hash
K - 子串翻转回文串2020ccpc河南省赛字符串哈希:将字符串变成x进制数对公式的理解:举个十进制数的例子:123456h[1]1;h[2]1*10212;h[3]12*103123;h[4]123*1041234;.........h[i]h[i-1]*xa[i];h[i]代表的恰巧是整个数的前缀用p[i]表…...

试题 算法训练 转圈游戏
问题描述 n个小伙伴(编号从0到n-1)围坐一圈玩游戏。按照顺时针方向给n个位置编号,从0到n-1。 最初,第0号小伙伴在第0号位置,第1号小伙伴在第 1 号位置,……,依此类推。 游戏规则如下&am…...

【uni-app教程】九、运行环境判断与跨端兼容
(1)开发环境和生产环境 uni-app 可通过 process.env.NODE_ENV 判断当前环境是开发环境还是生产环境,一般用于连接测试服务器或生产服务器的动态切换。 在HBuilderX 中,点击「运行」编译出来的代码是开发环境,点击「发行…...

扩展WSL2虚拟硬盘的大小
扩展WSL2虚拟硬盘的大小 1、在 Windows PowerShell 中终止所有 WSL 实例 wsl --shutdown2、查看 WSL 实例运行状态,确认关闭,并记住发行版的名称 wsl -l -v如果没有更改移动过发行版安装包位置,那么可以通过以下方法查找到发行版的安装包位…...

Win系统蓝牙设备频繁卡顿/断连 - 解决方案
Win系统蓝牙设备频繁卡顿/断连 - 解决方案前言常见网卡Intel无线网卡(推荐)Realtek无线网卡总结查看本机网卡解决方案更新驱动更换网卡(推荐)前言 无线网卡有2个模块,一个是WiFi,一个是蓝牙,因…...
Git学习入门(2)- 基本命令操作总结
个人博客:我的个人博客,各位大佬来玩1 创建 git仓库1.1 从现有工作目录中初始化新仓库需要到你需要用git管理的项目中输入以下命令:git init便会创建一个空的git项目,并且当前目录下会出现一个名为 .git 的目录, Git 需…...

SPringCloud:Nacos快速入门及相关属性配置
目录 一、Nacos快速入门 1、在父工程中添加spring-cloud-alilbaba的管理依赖 2、如果有使用eureka依赖,将其注释 3、添加nacos的客户端依赖 4、修改yml文件,注释eureka配置 5、启动测试 二、Nacos相关属性配置 1、Nacos服务分级存储 2、根据集群…...

医疗器械之模糊算法(嵌入式部分)
模糊控制 所谓模糊控制,就是对难以用已有规律描述的复杂系统,采用自然语言(如大,中,小)加以描述,借助定性的,不精确的以及模糊的条件语句来表达,模糊控制是一种基于语言的…...
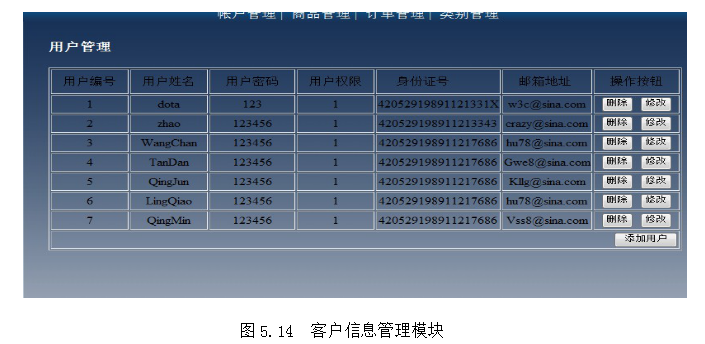
网上销售笔记本系统
技术:Java、JSP等摘要:本文讲述了基于B/S模式的笔记本电脑在线销售系统的设计与实现。所谓的笔记本电脑在线销售系统是通过网站推广互联企业的笔记本电脑和技术服务,并使客户随时可以了解企业和企业的产品,为客户提供在线服务和订…...
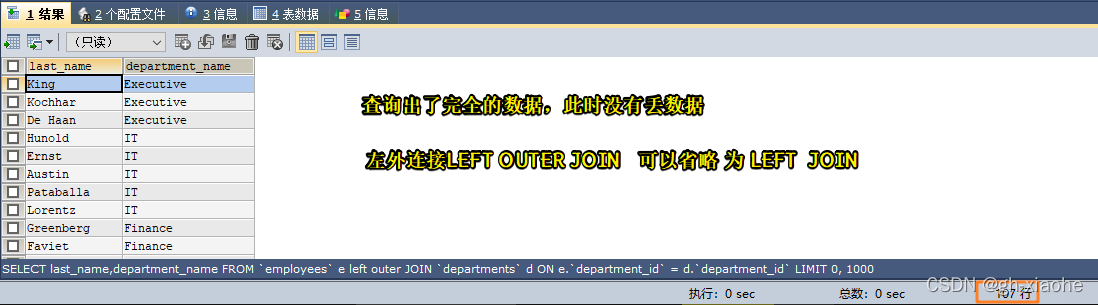
MySQL基础查询操作
文章目录🚏 Select语句🚀 一、SQL底层执行原理🚬 (一)、查询的结构🚬 (二)、SQL语句的执行过程🚭 1、WHERE 为什么不包含聚合函数的过滤条件?(面试…...

English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三
English Learning - L2 语音作业打卡 小元音 [ʌ] [ɒ] Day9 2023.3.1 周三💌发音小贴士:💌当日目标音发音规则/技巧:🍭 Part 1【热身练习】🍭 Part2【练习内容】🍭【练习感受】🍓元音 [ʌ]&…...
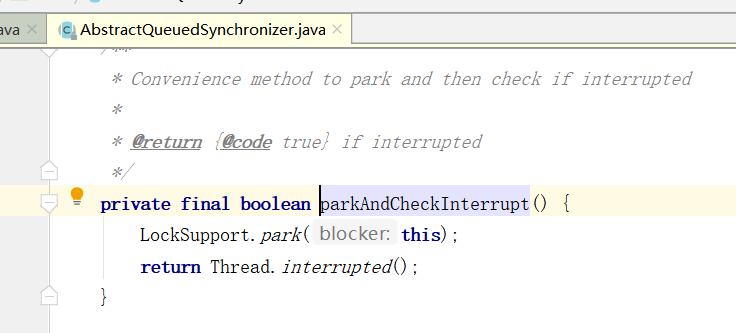
Condition 源码解读
一、Condition 在并发情况下进行线程间的协调,如果是使用的 synchronized 锁,我们可以使用 wait/notify 进行唤醒,如果是使用的 Lock 锁的方式,则可以使用 Condition 进行针对性的阻塞和唤醒,相较于 wait/notify 使用…...
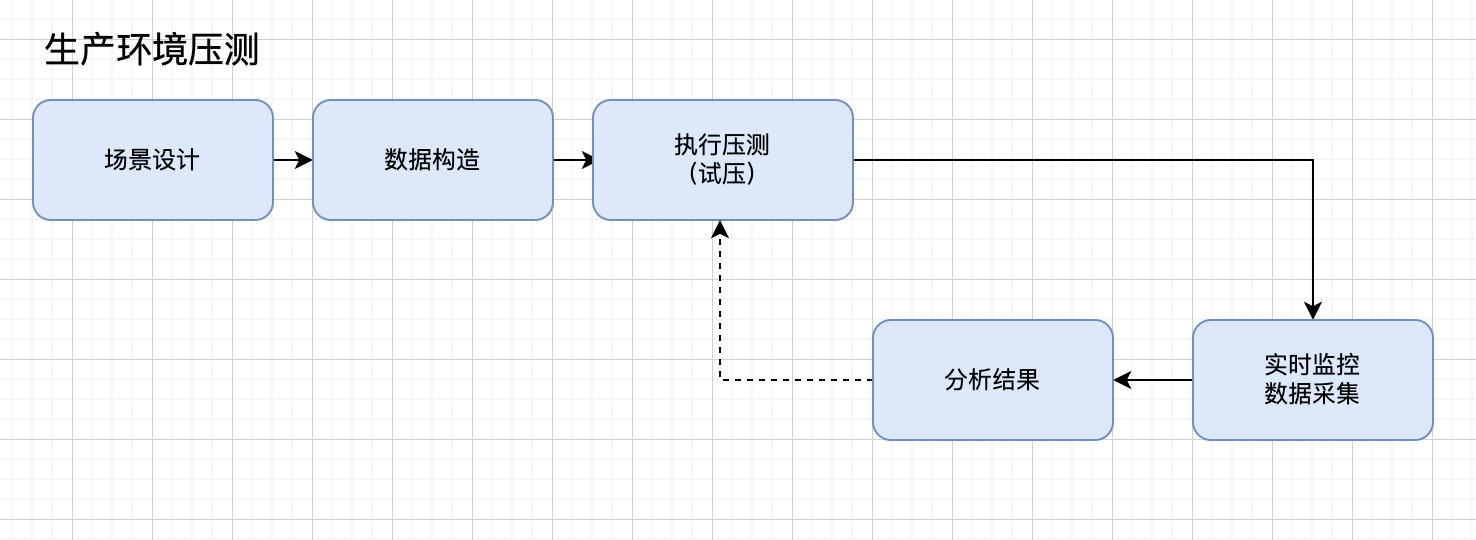
看完这篇入门性能测试
大家好,我是洋子。最近组内在进行服务端高并发接口的性能压测工作,起因是2023年2月2日,针对胡某宇事件进行新闻发布会直播,几十万人同时进入某媒体直播间,造成流量激增 从监控上可以看出,QPS到达某峰值后&…...

推导部分和——带权并查集
题解: 带权并查集 引言: 带权并查集是一种进阶的并查集,通常,结点i的权值等于结点i到根节点的距离,对于带权并查集,有两种操作需要掌握——Merge与Find,涉及到路径压缩与维护权值等技巧。 带…...
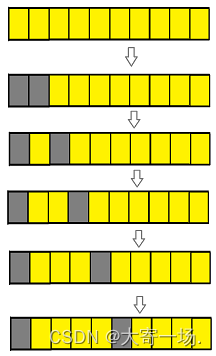
费解的开关/翻硬币
🌱博客主页:大寄一场. 🌱系列专栏: 算法 😘博客制作不易欢迎各位👍点赞⭐收藏➕关注 题目:费解的开关 你玩过“拉灯”游戏吗? 25盏灯排成一个 55 的方形。 每一个灯都有一个开关&…...
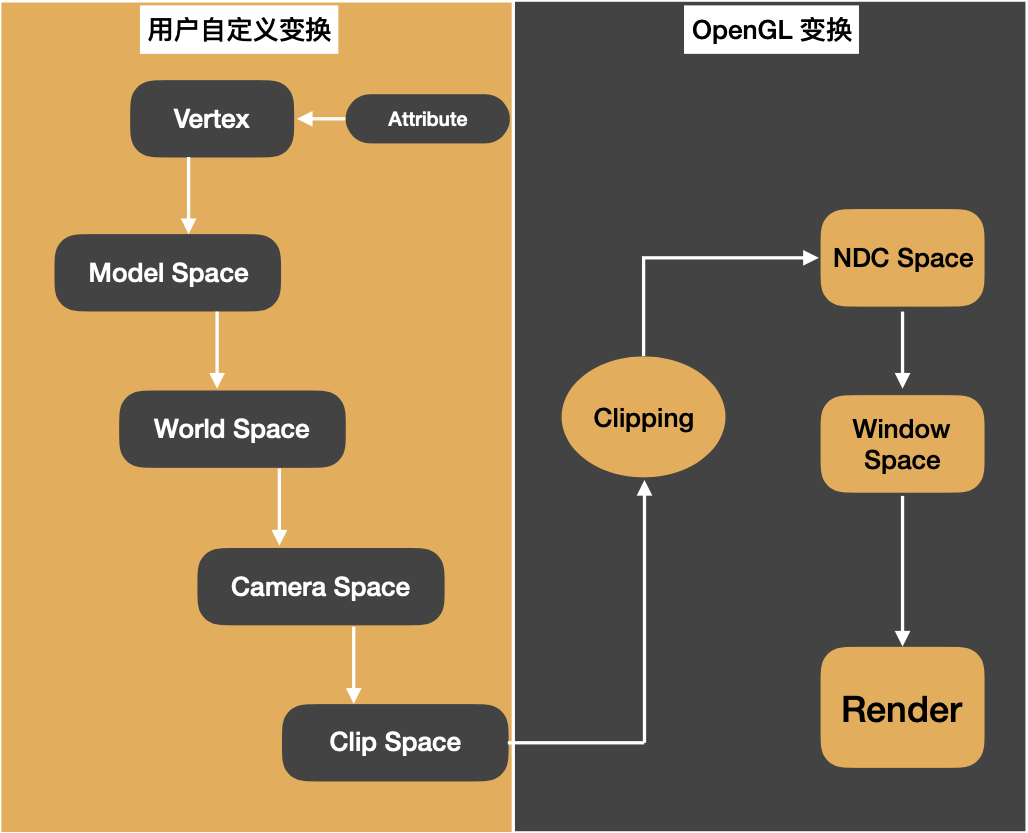
OpenGL中的坐标系
1、2D笛卡尔坐标系2D笛卡尔坐标系跟我们高中的时候学习的坐标系一样,是由x、y决定的。2、3D笛卡尔坐标系3D笛卡尔坐标系坐标由x、y、z决定,满足右手定则。3、视口glViewport(GLint x,GLint y,GLsizei width,GLsizei height)窗口和视口大小可以相同&#…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
