力扣刷题(DAY09-DAY11)
Day09
0958. 二叉树的完全性检验
知识点:完全二叉树:在一棵完全二叉树中,除了最后一层外,所有层都被完全填满,并且最后一层中的所有节点都尽可能靠左。最后一层(第
h层)中可以包含1到个节点,
当最后一层全部都满(
个节点)的时候,就称为满二叉树。
题目大意:给你一棵二叉树的根节点 root ,请你判断这棵树是否是一棵 完全二叉树 。
思路:尝试用层次遍历解决,如果存在上一个节点出队没有左孩子,但有右孩子,就是flase;
或者本节点都没有,但下一个有。可以设置bool will来判断 再深入思考一下,在遍历到当前节点的时候 ,前面如果已经出现过空节点,那他一定不是完全二叉树。
于是:层次遍历二叉树,无论节点是否存在,都放入队列中,当出现空节点的时候标记一下;继续遍历,如果后面还有结点,说明不是完全二叉树
其实也可以说完全二叉树,层次遍历到最后一个节点时一定不会出现空节点
class Solution {
public:bool isCompleteTree(TreeNode* root) {// 层次遍历bool will = 0;queue<TreeNode*> q;TreeNode* visited;q.push(root);while (!q.empty()) {visited = q.front();q.pop();if (visited == NULL) {will = 1; // 空节点} else {if (will) // 前面有一个空return false;q.push(visited->left);q.push(visited->right);}}return true;}
};这里强调说明一下:
visited = q.front(); 一定要放在前面写0543. 二叉树的直径
题目要求:
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。两节点之间路径的 长度 由它们之间边数表示。
思路:长度最长的路线应该是从左边的最高高度到右边的最高高度;根据边计算一下,应该是左hight+右hight-1---》左子树高度+柚子树高度;
好好好,按着这样写下去,出现这个情况了……
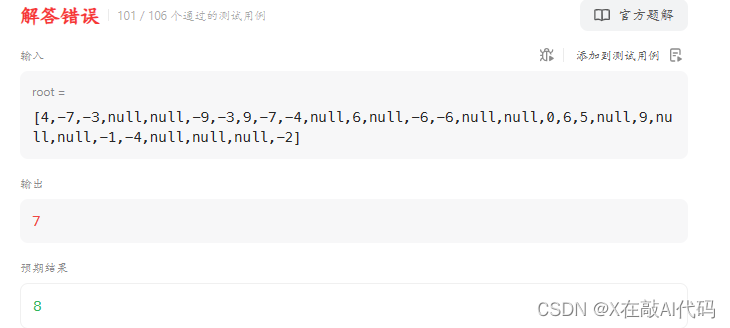
树大概张这个样子
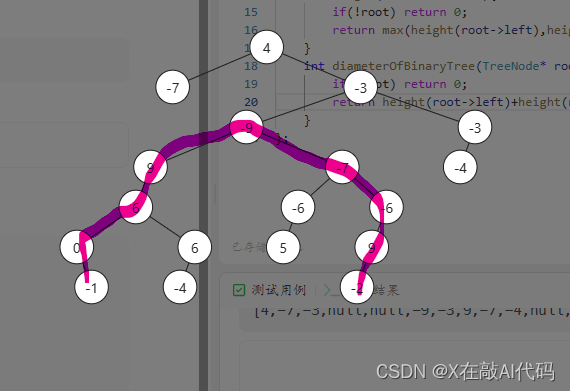
重新想思路:犯错原因只考虑了焦点在根节点的情况,
于是升级版:递归地计算每个节点的左子树和右子树的深度,并在遍历的过程中更新最大直径,最终得到整棵树的直径。
max_len=max(height(vistied->left)+height(vistied->right),max_len) ;
//visited 每个结点,用中序遍历一下吧;于是代码就有了:
class Solution {
public:int max_len=0;int height(TreeNode* root){//求高度if(!root) return 0;return max(height(root->left),height(root->right))+1;}void inorder(TreeNode* root){//每个结点,用中序遍历一下吧;if(!root) return;inorder(root->left);max_len=max(height(root->left)+height(root->right),max_len) ;inorder(root->right);}int diameterOfBinaryTree(TreeNode* root) {if(!root) return 0;inorder(root);return max_len;}
};思路有了,不放在优化一下
class Solution {
public:int diameterOfBinaryTree(TreeNode* root) {int maxDiameter = 0;maxDepth(root, maxDiameter);return maxDiameter;}int maxDepth(TreeNode* node, int& maxDiameter) {if (node == nullptr) {return 0;}int leftDepth = maxDepth(node->left, maxDiameter);int rightDepth = maxDepth(node->right, maxDiameter);maxDiameter = max(maxDiameter, leftDepth + rightDepth);return 1 + max(leftDepth, rightDepth);}
};
0662. 二叉树最大宽度
题目大意:
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
想到一种这个情况,测试结果为4;
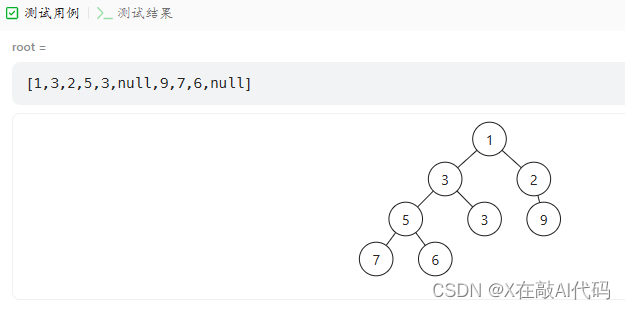
思路:求层的宽度,当然是层次遍历bfs啦,那怎么保证左孩子不存在,右孩子还能存进去的?
还记得树的顺序存储么?用这个就好。left_index=双亲*2;right_index=双亲*2+1;
这样我们层次遍历是,可以建立二维队列
queue<pair<TreeNode*, unsigned long long>> q;为什么unsigned longlong 呢? 因为题目所给的数据范围是3000个节点,如果没层一个节点且都靠右排列,那么会有1000多层的树。 这样导致在树底部的节点编号为2的一千多次方。而这个范围在多数语言中都是没办法正常处理的。
class Solution {
public:int widthOfBinaryTree(TreeNode* root) {if (!root) return 0;int max_width = 0;queue<pair<TreeNode*, unsigned long long>> q;q.push({root, 1});while (!q.empty()) {int size = q.size();unsigned long long leftmost = q.front().second;unsigned long long rightmost = leftmost;for (int i = 0; i < size; i++) {auto [node, index] = q.front();q.pop();if (i == 0) {leftmost = index;}if (i == size - 1) {rightmost = index;}if (node->left) {q.push({node->left, 2 * index});}if (node->right) {q.push({node->right, 2 * index + 1});}}max_width = max(static_cast<int>(rightmost - leftmost + 1), max_width);}return max_width;}
};
好了,今天就到这里 over
相关文章:

力扣刷题(DAY09-DAY11)
Day09 0958. 二叉树的完全性检验 知识点:完全二叉树:在一棵完全二叉树中,除了最后一层外,所有层都被完全填满,并且最后一层中的所有节点都尽可能靠左。最后一层(第 h 层)中可以包含 1 到 个节点…...

IPC之管道
什么是管道? 管道的本质是操作系统在内核中创建出的一块缓冲区,也就是内存 管道的应用 $ ps aux | grep xxx ps aux 的标准输出写到管道,grep 从管道这块内存中读取数据来作为它的一个标准输入,而且 ps 和 grep 之间是兄弟关系&a…...

VUE-组件间通信(二)$emit
$emit 1、单向绑定 子组件向父组件传值 2、使用示例 父组件 <template><div id"app"><!-- 监听自定义触发事件 emitInvokeEvents--><SonDemo emitInvokeEvents"fatherFunction"></SonDemo></div> </template&…...

java 程序连接 redis 集群 的时候报错 MUTLI is currently not supported in cluster mode
找了半天找不到,为什么国内文章环境是真的差, redis 集群不支持事务,而你的方法上面估计使用了 spring 的事务导致错误具体解决: Transactional(propagation Propagation.NOT_SUPPORTED)public <T> void removeMultiCacheMapValue…...
AVP-SLAM:自动泊车系统中的语义SLAM_
AVP-SLAM:自动泊车系统中的语义SLAM 附赠最强自动驾驶学习资料:直达链接 ●论文摘要 在自动代客泊车系统中车辆在狭窄且拥挤且没有GPS信号的停车场中进行导航,具备准确的定位能力是至关重要的。传统的基于视觉的方法由于在停车场中由于缺少…...
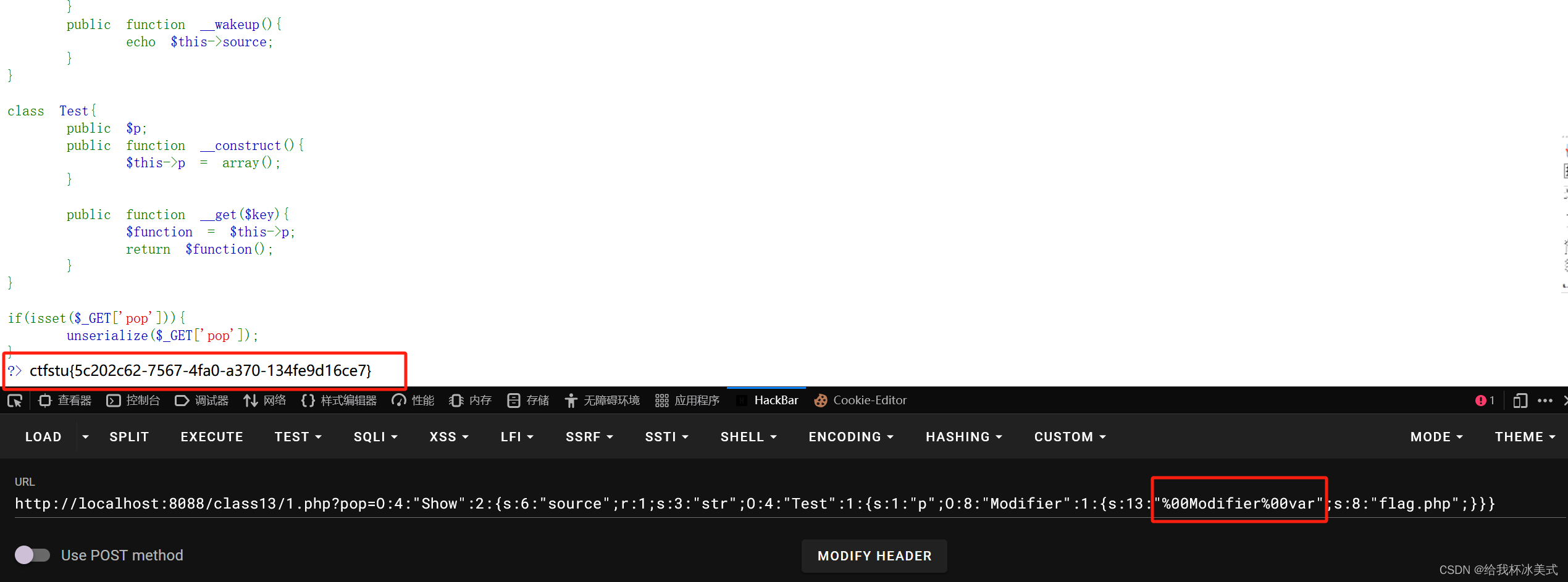
PHP反序列化--pop链
目录 一、了解pop链 1、pop链: 2、pop链触发规则: (1)通过普通函数触发: (2)通过魔术方法触发: 3、pop链魔术方法例题: 一、了解pop链 1、pop链: pop链…...
表示的含义(51为例))
单片机中的几种周期(振动/时钟,状态,机械,指令周期)表示的含义(51为例)
几种周期含义及个人理解描述 参考:短文,参考,百度 个人理解简述:对于几个周期性来说,可以认为是小单位的时间组合成了长时间。就像把一个数据赋值,这个是简单的一个机械周期能完成的动作,但需要…...
Spring Boot+Vue前后端分离项目如何部署到服务器
🌟 前言 欢迎来到我的技术小宇宙!🌌 这里不仅是我记录技术点滴的后花园,也是我分享学习心得和项目经验的乐园。📚 无论你是技术小白还是资深大牛,这里总有一些内容能触动你的好奇心。🔍 &#x…...

【学习总结】Ubuntu中vscode用ROS插件调试C++程序
1、教程 参考博客: 【ROS】 在VScode中 ROS Debug 配置方法非常详细版 关于launch文件的配置: launch.json {"version": "0.2.0","configurations": [{"name": "ROS: Launch","request"…...

html--蝴蝶
<!DOCTYPE html> <html lang"en" > <head> <meta charset"UTF-8"> <title>蝴蝶飞舞</title> <link rel"stylesheet" href"https://cdnjs.cloudflare.com/ajax/libs/meyer-reset/2.0/reset.min.cs…...
方法和 yield()方法有什么区别?为什么 Thread 类的 sleep()和 yield ()方法是静态的?)
线程的 sleep()方法和 yield()方法有什么区别?为什么 Thread 类的 sleep()和 yield ()方法是静态的?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 线程的 sleep()方法和 yield()方法有什么区别 sleep()方法: sleep()方法使当前线程进入休眠状态,即暂停执行一段时间。它是静态方法,属于Thread类,调用…...

Java进阶 Maven基础
资料格式 配置文件 com.itheima Java代码 Statement stat con.createStatement(); 示例 com.itheima 命令 mvn test - Maven简介 传统项目管理状态分析 Maven 是什么 Maven的本质是一个项目管理工具,将项目开发过程抽象成一个项目对象模型(POM&…...
:SpringBoot 整合Apache tika 实现文档内容解析)
Spring Boot(六十八):SpringBoot 整合Apache tika 实现文档内容解析
1 Apache Tika 介绍 Apache Tika 是一个开源的内容检测和分析框架,由Apache软件基金会开发和维护的顶级项目。它可以从各种格式的文件中提取元数据和文本内容。Tika非常适合处理全文搜索、内容分析、翻译、内容提取等需要大量处理和分析文档内容的任务。Apache Tika提供了多种…...

jQuery+CSS3自动轮播焦点图特效源码
jQueryCSS3自动轮播焦点图特效源码,源码由HTMLCSSJS组成,双击html文件可以本地运行效果,也可以上传到服务器里面 下载地址 jQueryCSS3自动轮播焦点图特效源码...

面试经典150题(114-118)
leetcode 150道题 计划花两个月时候刷完之未完成后转,今天完成了5道(114-118)150 gap 了一周,以后就不记录时间了。。 114.(70. 爬楼梯) 题目描述: 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不…...

HTML表单标签详解:如何用HTML标签打造互动网页?
在互联网的世界中,表单是用户与网站进行互动的重要桥梁。无论是注册新账号、提交反馈、还是在线购物,表单都扮演着至关重要的角色。在网页中,我们需要跟用户进行交互,收集用户资料,此时就需要用到表单标签。 HTML提供…...
Web 服务器-Tomcat
文章目录 Web服务器一、Tomcat简介二、基本使用三、在IDEA中创建Maven Web项目四、在IDEA中使用Tomcat Web服务器 一、Tomcat简介 二、基本使用 三、在IDEA中创建Maven Web项目 四、在IDEA中使用Tomcat...
(德迅零域)微隔离安全平台是什么,有什么作用?
网络隔离并不是新的概念,而微隔离技术(Micro-Segmentation)是VMware在应对虚拟化隔离技术时提出来的,但真正让微隔离备受大家关注是从2016年起连续3年微隔离技术都进入Gartner年度安全技术榜单开始。在2016年的Gartner安全与风险管…...

这些问题,每年软考报名时都有人问
软考报名实行网上在线报名的方式,每次在报名期间,考生都会遇到各种各样的问题,本文挑选了一些大家问的比较多的问题进行了解答,希望对大家有所帮助。 1、软考报名资格审核要审核多久? 一般来说审核时间在3个工作…...

JavaScript爬虫进阶攻略:从网页采集到数据可视化
在当今数字化世界中,数据是至关重要的资产,而网页则是一个巨大的数据源。JavaScript作为一种强大的前端编程语言,不仅能够为网页增添交互性,还可以用于网页爬取和数据处理。本文将带你深入探索JavaScript爬虫技术的进阶应用&#…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...
