力扣练习 3.27
121. 买卖股票的最佳时机
贪婪思想:力争在最低成本买入,最高利润卖出。
[7,1,5,3,6,4]
可以先假设在第一天买入和卖出,这时最低成本是7,最大利润是7-7=0
然后假设在第二天买入和卖出,成本就是1,利润也是0
第三天因为成本比第二天高,所以不买入,只卖出,利润就是5-1=4
以此类推
每次遍历都检测最小成本和最大利润
class Solution:def maxProfit(self, prices: List[int]) -> int:# 贪婪思想,初始化成本和利润cost, profit = float('inf'), 0# 成本是取最小的,利润是选最大的# 遍历过程中不断更新最小成本和最大利润for price in prices:cost = min(cost, price)profit = max(profit, price-cost)return profit122. 买卖股票的最佳时机 II
单独的交易:看今天卖和昨天买的差值
连续上涨:等差数列
class Solution:def maxProfit(self, prices: List[int]) -> int:# 初始化利润profit = 0# 如果当前比前一天的价格更高,那就是要昨天买今天买# 对于等差数列,在同一天卖跟每天都卖是一样的for i in range(1, len(prices)):# 把所有天的利润加起来,如果是负利润,那么就是0(不卖)temp = max(prices[i]-prices[i-1], 0)profit += tempreturn profit
300. 最长递增子序列
要找到一个数组中最长严格递增子序列(Longest Increasing Subsequence,简称LIS)的长度,动态规划是一种有效的方法。这个问题的关键在于找出一个状态定义,使得状态之间的转移是可解的。
动态规划解法:
状态定义:定义
dp[i]为考虑前i个元素,以第i个数字结尾的最长递增子序列的长度。注意,这里的子序列至少包含一个数,即第i个数本身。状态转移方程:要计算
dp[i],需要考虑比第i个数小的所有数。对于任意一个小于i的下标j,如果nums[j] < nums[i],那么nums[i]可以接在nums[j]后面形成一个更长的递增子序列。因此,dp[i] = max(dp[i], dp[j] + 1)对所有的0 <= j < i且nums[j] < nums[i]。初始化:因为最长递增子序列至少包含自己,所以每个元素的LIS长度初始值至少为1,即
dp[i] = 1。计算顺序:从左到右依次计算每个
dp[i],因为计算dp[i]时需要用到前面的dp[j]。结果:最长递增子序列的长度为所有
dp[i]中的最大值。
代码实现
def lengthOfLIS(nums):if not nums:return 0n = len(nums)dp = [1] * n # 初始化dp数组,每个元素的LIS长度初始值为1for i in range(1, n):for j in range(i):if nums[j] < nums[i]:dp[i] = max(dp[i], dp[j] + 1)return max(dp) # LIS长度为dp数组中的最大值
1143. 最长公共子序列
解题思路:动态规划
需要构建辅助矩阵,多加一行和一列
当前的状态由左上、左边和上边决定。如果相等,那么当前状态是由左对角线(左上角)的加自己1决定的;如果不相等,那么当前状态需要在左边和上边中选择一个最大的扩展其状态。
步骤 1:
理解问题和目标 我们的目标是找出两个字符串
text1和text2的最长公共子序列的长度。一个子序列是指从原字符串中删除一些(或不删除)字符而不改变其余字符的顺序得到的新字符串。步骤 2:
定义 DP 数组 定义二维数组
dp,其中dp[i][j]表示text1中前i个字符和text2中前j个字符的最长公共子序列的长度。注意,dp[i][j]是基于text1[0..i-1]和text2[0..j-1]的子序列。步骤 3:
找出状态转移方程
- 如果
text1[i-1] == text2[j-1],即当前两个字符相等,那么dp[i][j] = dp[i-1][j-1] + 1。因为我们找到了一个公共元素,可以在以前的LCS长度上加1。- 如果
text1[i-1] != text2[j-1],即当前两个字符不相等,那么dp[i][j] = max(dp[i-1][j], dp[i][j-1])。此时,LCS的长度是两种情况中的较大值。步骤 4:
初始化 DP 数组 初始化
dp数组的第一行和第一列为0,因为任何字符串与空字符串的最长公共子序列长度都是0。步骤 5:
填充 DP 数组 从
dp[1][1]开始,根据状态转移方程逐步填充整个dp数组。步骤 6:
解读结果
dp数组的最后一个元素dp[len(text1)][len(text2)]即为text1和text2的最长公共子序列的长度。
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:# 辅助矩阵m, n = len(text1), len(text2)# 都加1个维度,方便后续操作不超索引dp = [[0]*(m+1) for _ in range(n+1)]for i in range(1, n+1): # 先从第一个维度遍历for j in range(1, m+1): #从第二个维度遍历if text1[j-1] == text2[i-1]: # 因为是从1开始,所以要看前面的一位dp[i][j] = dp[i-1][j-1]+1 # 相等,那么就是加上前面的最长子序列和当前的元素else:dp[i][j] = max(dp[i-1][j], dp[i][j-1]) # 不相等,就将左边对角线附近的最长子序列数扩展到当前return dp[n][m]
64. 最小路径和
动态规划
建立一个辅助矩阵,第一行和第一列的路径和只能是从左边或者右边来,所以辅助矩阵维度保持不变,初始化为0,将第一行第一列的值按照路径和定义加进来。
状态转移公式就是dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
class Solution:def minPathSum(self, grid: List[List[int]]) -> int:m = len(grid)n = len(grid[0])dp = [[0] * (n) for _ in range(m)]# 初始化起点dp[0][0] = grid[0][0]# 初始化第一列,每个位置只能从上方来for i in range(1, m):dp[i][0] = dp[i-1][0] + grid[i][0]# 初始化第一行,每个位置只能从左边来for j in range(1, n):dp[0][j] = dp[0][j-1] + grid[0][j]# 动态规划for i in range(1, m):for j in range(1, n):# 选择左边和上面的最小值加上当前值dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]return(dp[-1][-1]) # 输出最后一个位置的值,即右下角的最小路径和72. 编辑距离
解题思路:动态规划,不用管具体改了什么字符,只管当前状态由什么决定。一般都是跟左边、上边、左上有关。
解释这三个操作对应的状态转移方程,我们先要理解每个操作的含义和如何影响字符串的转换:
插入:
dp[i][j] = dp[i][j-1] + 1
- 这意味着为了从
word1的前i个字符转换到word2的前j个字符,我们考虑了在word1的前i个字符基础上,通过在末尾插入一个与word2[j-1]相同的字符,使其与word2的前j个字符匹配。因为我们插入了一个字符,所以操作次数加1。- 插入操作是基于假设我们已经找到了将
word1的前i个字符转换为word2的前j-1个字符的最优方法,并在此基础上进行一次插入操作。删除:
dp[i][j] = dp[i-1][j] + 1
- 这表示为了将
word1的前i个字符转换为word2的前j个字符,我们考虑了从word1的前i个字符中删除最后一个字符,使其与word2的前j个字符更接近。因为我们进行了删除操作,所以操作次数加1。- 删除操作是基于假设我们已经找到了将
word1的前i-1个字符转换为word2的前j个字符的最优方法,并在此基础上进行一次删除操作。替换:
dp[i][j] = dp[i-1][j-1] + 1
- 这意味着为了从
word1的前i个字符转换到word2的前j个字符,我们考虑了将word1的第i个字符替换为word2的第j个字符(这两个字符不同),使之匹配。因为我们替换了一个字符,所以操作次数加1。- 替换操作是基于假设我们已经找到了将
word1的前i-1个字符转换为word2的前j-1个字符的最优方法,并在此基础上进行一次替换操作。这些状态转移方程的核心思想是,通过局部最优解(即最少的操作次数)来逐步构建全局最优解。在每个位置
dp[i][j],我们都尝试三种操作,并从中选择一种使得总操作数最小的方案,以此保证最终得到的是将整个word1转换为word2所需的最少操作次数。
class Solution:def minDistance(self, word1: str, word2: str) -> int:m,n = len(word1), len(word2)# 动态规划dp = [[0]*(n+1) for _ in range(m+1)]# 初始化左上角dp[0][0] = 0# 初始化第一行for i in range(1, m+1):dp[i][0] = i# 初始化第一列for j in range(1, n+1):dp[0][j] = jfor i in range(1, m+1):for j in range(1, n+1):# 如果字符相等if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1] # 那就不操作,继承以前的操作else:dp[i][j] = min(dp[i][j-1], dp[i-1][j], dp[i-1][j-1]) + 1 # 否则,就操作,加上当前字符return(dp[m][n])
62. 不同路径
解题思路:又是动态规划。
要确定的点是当前状态是个啥,比如上题就是操作数,这题就是路径数;
然后确定当前状态被什么决定,比如上题是根据左上、左边、上边,本题就是根据左边和上边,理解题意后写出状态转移公式,代码化。
class Solution:def uniquePaths(self, m: int, n: int) -> int:# 辅助矩阵dp = [[1]*n for _ in range(m)]# 状态转移公式for i in range(1, m):for j in range(1, n):# 当前状态是指从原点到当前点的路径总和,由从上和左边来的路径决定dp[i][j] = dp[i-1][j] + dp[i][j-1]return(dp[-1][-1])
考虑到机器人每次只能向下或者向右移动,我们可以发现到达网格中任意位置
(i, j)的路径数是到达其上方位置(i-1, j)
和左侧位置(i, j-1)的路径数之和。这是因为,从起点到达(i, j)的每条路径,都是通过最后一步从(i-1, j)
或(i, j-1)移动过来的。基于这个原理,我们可以构建一个动态规划方程来求解问题。动态规划方法
状态定义:定义
dp[i][j]为从起点(0, 0)到达点(i, j)的路径总数。状态转移方程:因为到达点
(i, j)只能从(i-1, j)或(i, j-1)两个点移动一步到达,所以dp[i][j] = dp[i-1][j] + dp[i][j-1]。初始化:初始化第一行和第一列的值为1,因为从起点到达第一行和第一列的任意位置只有一种路径(要么一直向右,要么一直向下)。
填表:按顺序计算
dp数组的其余部分。结果:
dp[m-1][n-1]即为从起点到达终点的路径总数。解释
- 初始化时,
dp的每个元素都被设置为1,因为到达第一行或第一列的任意位置的路径只有一条。- 通过双层循环,我们更新
dp数组的值,使其反映到达每个位置的路径数。- 最后,
dp[m-1][n-1]存储了到达右下角的路径总数。这种动态规划方法利用了问题的子结构(问题的解可以通过其子问题的解来构建)和重叠子问题(相同的子问题被多次计算)特点,使得我们可以高效地求解原问题。
152. 乘积最大子数组
要解决这个问题,我们可以同时跟踪到当前位置为止的最大乘积和最小乘积(因为一个很小的负数乘以一个负数可能变成一个很大的正数)。这意味着我们需要维护两个动态规划数组,一个用于追踪最大乘积,另一个用于追踪最小乘积。
修改后的算法:
定义状态:
max_dp[i]表示到第i个元素为止的最大连续子数组乘积。min_dp[i]表示到第i个元素为止的最小连续子数组乘积(考虑负负得正的情况)。状态转移方程:
- 对于每个
i,有三种情况需要考虑(nums[i]本身、nums[i] * max_dp[i-1]和nums[i] * min_dp[i-1]),因为当前元素可以独自成为最大乘积子数组,或者可以与前一个子数组的最大/最小乘积相乘形成新的最大/最小乘积。max_dp[i] = max(nums[i], nums[i] * max_dp[i-1], nums[i] * min_dp[i-1])min_dp[i] = min(nums[i], nums[i] * max_dp[i-1], nums[i] * min_dp[i-1])初始化:
max_dp[0] = min_dp[0] = nums[0],因为第一个元素前面没有其他元素,所以它自己就是一个子数组。遍历数组:
- 按照状态转移方程更新
max_dp和min_dp。找到最大乘积:
- 最大乘积不一定是
max_dp[-1],因为最大乘积可能出现在数组的任何位置,所以需要遍历max_dp数组找到最大值。
class Solution:def maxProduct(self, nums: List[int]) -> int:# 因为负负得正,所以不能只看大于0的,维护两个辅助数组max_dp = [1] * len(nums)min_dp = [1] * len(nums)max_dp[0] = nums[0]min_dp[0] = nums[0]# 最大乘积的数组状态由当前元素;如果前面是正的,乘当前;最小乘积有可能是负的,当前也可能是负的for i in range(1, len(nums)):max_dp[i] = max(nums[i], max_dp[i-1]*nums[i], min_dp[i-1]*nums[i])min_dp[i] = min(nums[i], max_dp[i-1]*nums[i], min_dp[i-1]*nums[i])return max(max_dp)
198. 打家劫舍
问题的关键是找到一个状态定义,以及如何根据前面的状态来更新当前的状态。问题可以描述为:给定一个整数数组,从中选取出一些元素,这些元素的总和最大,但不能选取相邻的元素。
动态规划思路
状态定义:定义
dp[i]为到达第i个房屋时能够偷窃到的最高金额。状态转移方程:对于第
i个房屋,有两种选择:
- 不偷这个房屋,那么总金额就是到前一个房屋为止的最高金额,即
dp[i-1];- 偷这个房屋,那么总金额就是这个房屋的金额加上到前前个房屋为止的最高金额,即
nums[i] + dp[i-2](因为不能偷相邻的房屋)。
所以,dp[i] = max(dp[i-1], nums[i] + dp[i-2])。初始化:
dp[0] = nums[0],只有一个房屋时,只能偷这一个;- 如果有两个房屋,应该选择金额较大的那个,所以
dp[1] = max(nums[0], nums[1])。计算顺序:从左到右依次计算每个
dp[i]。
class Solution:def rob(self, nums: List[int]) -> int:# 处理只有一个元素的情况if len(nums) == 1:return nums[0]# 直接复制数组作为辅助数组dp = nums.copy()# 第二个状态取前两个的最大值dp[1] = max(nums[0], nums[1])# dp的当前状态是到当前的最高金额(和)for i in range(2, len(nums)):# 要么不偷,要么偷dp[i] = max(dp[i-1], dp[i-2] + nums[i])return dp[-1]
相关文章:

力扣练习 3.27
121. 买卖股票的最佳时机 贪婪思想:力争在最低成本买入,最高利润卖出。 [7,1,5,3,6,4] 可以先假设在第一天买入和卖出,这时最低成本是7,最大利润是7-70 然后假设在第二天买入和卖出,成本就是1,利润也是0 第…...

C 指向指针的指针
指向指针的指针是一种多级间接寻址的形式,或者说是一个指针链。通常,一个指针包含一个变量的地址。当我们定义一个指向指针的指针时,第一个指针包含了第二个指针的地址,第二个指针指向包含实际值的位置。 一个指向指针的指针变量…...

通俗易懂:新生代、老年代和永久代/元空间的具体含义是什么?
在Java虚拟机(JVM)的内存管理中,堆内存通常被划分为几个不同的区域,以便更有效地管理和回收内存。以下是新生代(Young Generation)、老年代(Old Generation)和永久代/元空间…...

Centos7.9备份mysql数据库
1. 备份 备份shell脚本 [rootiZoqvrzbtnzd6kZ local]# vi mysql_backup.sh #!/bin/bash #设置MySQL登录信息 MYSQL_USER"root" MYSQL_PASSWORD"**********" MYSQL_DATABASE"ubox" BACKUP_DIR"/usr/local/mysql_backup" MONTH"…...
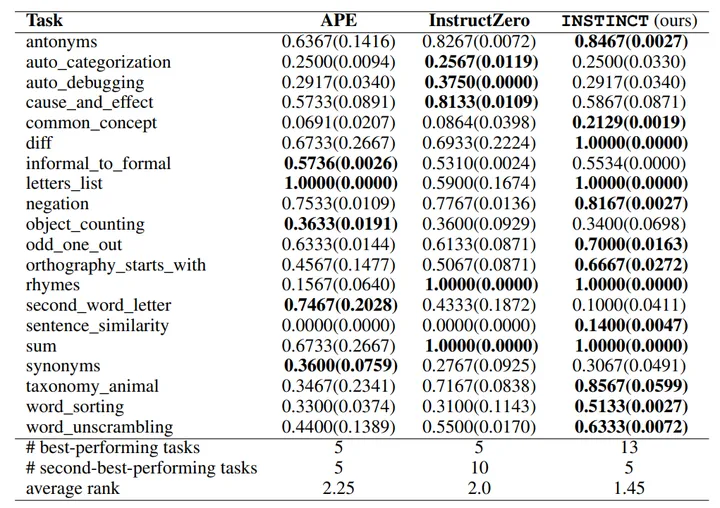
Automatic Prompt Engineering
让大模型自己生成prompt,生成提示(prompt)存在两种不同的操作方式。第一种方式是在文本空间中进行,这种提示以离散的文本形式存在。第二种方式是将提示抽象成一个向量,在特征空间中进行操作,这种提示是抽象…...

Spring高级面试题-2024
Spring 框架中都用到了哪些设计模式? 1. 简单工厂: ○ BeanFactory:Spring的BeanFactory充当工厂,负责根据配置信息创建Bean实例。它是一种工厂模式的应用,根据指定的类名或ID创建Bean对象。2. 工厂方法ÿ…...
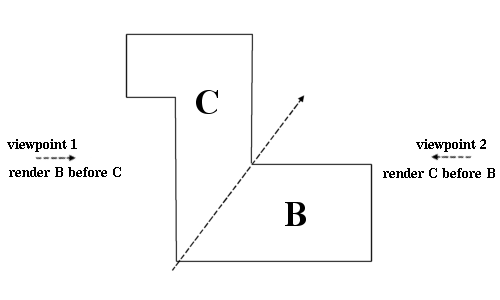
用BSP优化3D渲染
3D渲染引擎设计者面临的最大问题之一是可见性计算:只必须绘制可见的墙壁和物体,并且必须以正确的顺序绘制它们(应该在远处的墙壁前面绘制近墙) 。 更重要的是,对于游戏等应用程序来说,开发能够快速渲染场景…...

Composer常见错误解决
Composer 是 PHP 社区广泛使用的一个依赖管理工具,它帮助开发者定义、管理和安装项目所需的库。在使用 Composer 的过程中,可能会遇到各种错误和问题。以下是一些常见的 Composer 错误及其解决方法: 1. 内存限制错误 错误信息:P…...
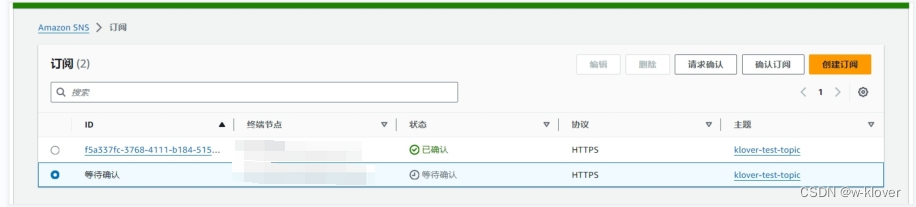
amazon中sns的使用
使用网页配置订阅 创建主题>使用标准>自定义名称>其他默认 点击创建即可 创建订阅 订阅策略配置(不配置,会推送给多个人,除非你每个都创建主题) 注意: 可以你可以随便写,后面的值只能是对象&am…...
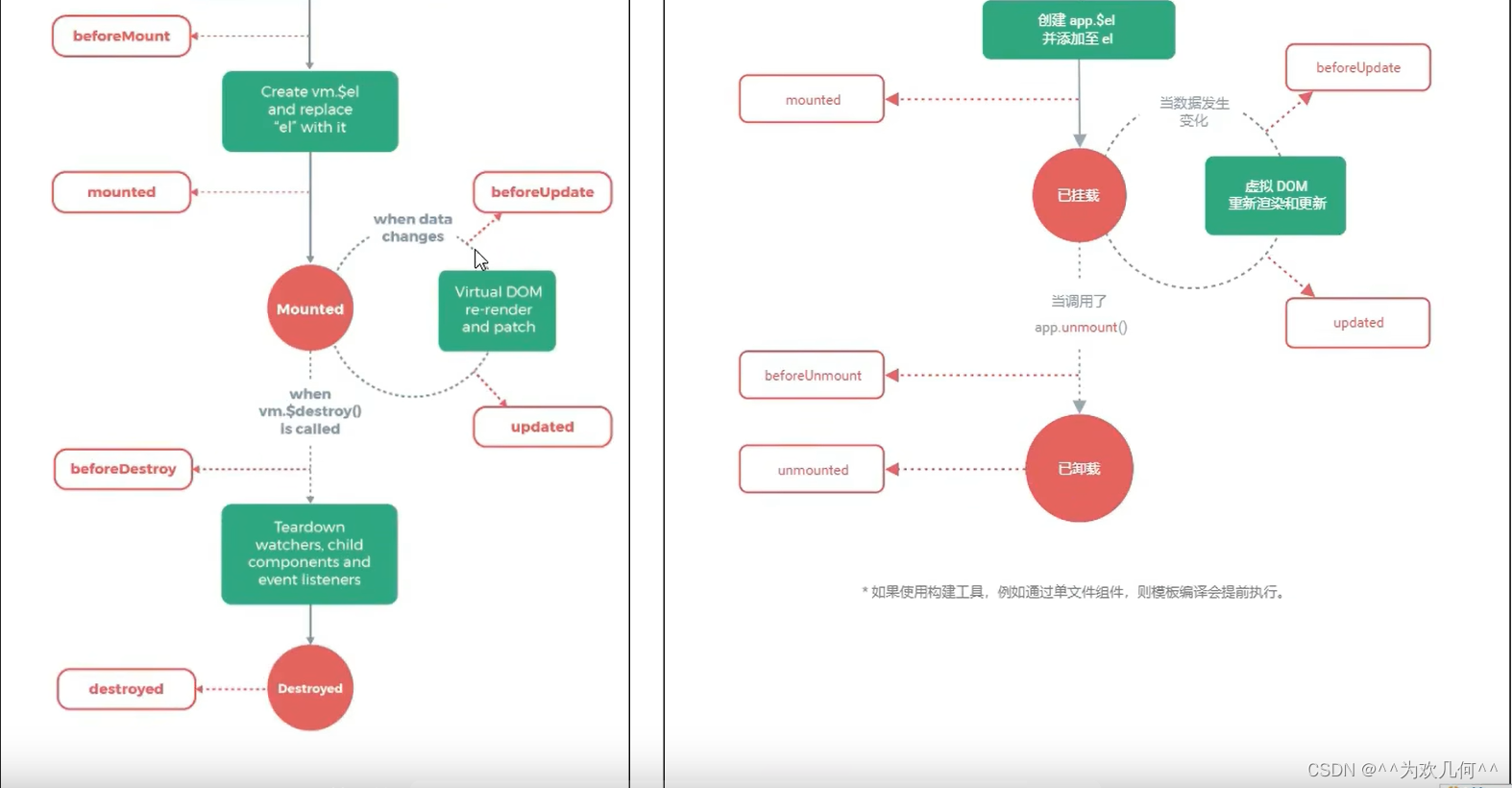
web前端面试题----->VUE
Vue的数据双向绑定是通过Vue的响应式系统实现的。具体原理: 1. Vue会在初始化时对数据对象进行遍历,使用Object.defineProperty方法将每个属性转化为getter、setter。这样在访问或修改数据时,Vue能够监听到数据的变化。 2. 当数据发生变化时…...

计算机领域热门技术词汇
文章目录 计算机领域热门技术词汇1、机器学习 machine learning2、神经网络 neural network3、深度学习 deep learning4、自然语言处理 natural language processing5、计算机视觉 computer vision6、大数据 big data7、数据挖掘 data mining(DM)8、云计…...

jsp指令和动作
1.page指令:描述页面信息 pageENcoding:软件编码 contentType:浏览器编码 2.include指令:将多个网页合成一个网页,静态包含网页 问题:1.在网页源代码中,会形成错误的多遍代码,将主页面代码和…...
手撕算法-最小覆盖子串
描述 分析 滑动窗口。 参考力扣官方的题解思路 本问题要求我们返回字符串 s 中包含字符串 t 的全部字符的最小窗口。我们称包含 t 的全部字母的窗口为「可行」窗口。 我们可以用滑动窗口的思想解决这个问题。在滑动窗口类型的问题中都会有两个指针,一个用于「延伸…...

TrOCR—基于Transformer的OCR入门
导 读 本文主要介绍TrOCR:基于Transformer的OCR入门。 背景介绍 多年来,光学字符识别 (OCR) 出现了多项创新。它对零售、医疗保健、银行和许多其他行业的影响是巨大的。尽管有着悠久的历史和多种最先进的模型,研究人员仍在不断创新。与深…...
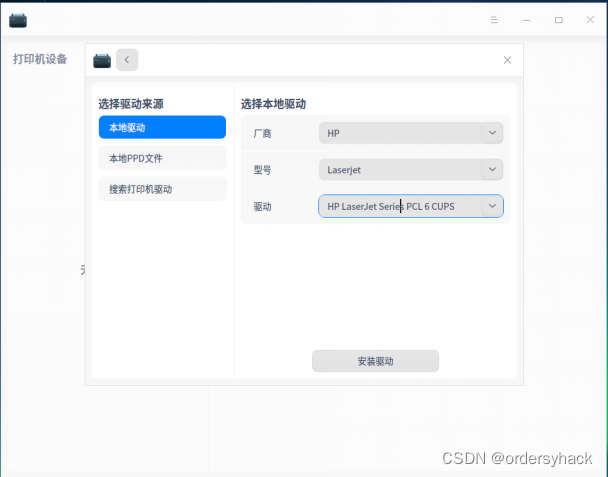
WIN使用LPD协议来共享打印机含统信UOS
打开“控制面板”,“程序和功能”,“启动或关闭Windows功能”,下拉找到“打印和文件服务”,勾选“LPD打印服务”和“LPR端口监视器”。确定之后重启电脑,共享主机和其它需要添加共享打印机的都开启功能和重启。 一、启…...
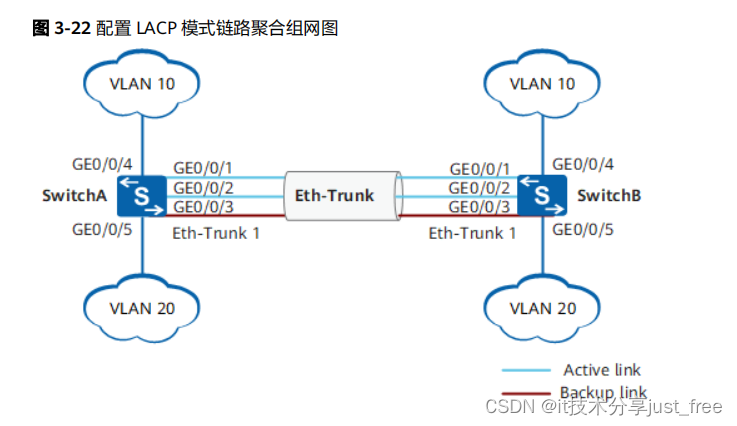
huawei 华为 交换机 配置 LACP 模式的链路聚合示例 (交换机之间直连)
组网需求 如 图 3-22 所示, SwitchA 和 SwitchB 通过以太链路分别都连接 VLAN10 和 VLAN20 的网络,且SwitchA 和 SwitchB 之间有较大的数据流量。用户希望 SwitchA 和 SwitchB 之间能够提供较大的链路带宽来使相同VLAN 间互相通信。在两台 Switch 设备上…...

c++ 有名对象和匿名对象
c 有名对象和匿名对象 有名对象就是有名字的对象,匿名对象就是没有名字的对象。 #define _CRT_SECURE_NO_WARNINGS 1 using namespace std; #include<iostream> class score { public:score(){math 100;chinese 100;english 100;}score(int _math, int _…...

day 36 贪心算法 part05● 435. 无重叠区间 ● 763.划分字母区间 ● 56. 合并区间
一遍过。首先把区间按左端点排序,然后右端点有两种情况。 假设是a区间,b区间。。。这样排列的顺序,那么 假设a[1]>b[0],如果a[1]>b[1],就应该以b[1]为准,否则以a[1]为准。 class Solution { public:static bo…...

【数据结构与算法】快速排序(详解:快排的Hoare原版,挖坑法和双指针法|避免快排最坏时间复杂度的两种解决方案|小区间优化|非递归的快排)
引言 快速排序作为交换排序的一种,在排序界的影响力毋庸置疑,我们C语言中用的qsort,C中用的sort,底层的排序方式都是快速排序。相比于同为交换排序的冒泡,其效率和性能就要差的多了,本篇博客就是要重点介绍…...

三位数组合-第12届蓝桥杯选拔赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第42讲。 三位数组合&#…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

新版NANO下载烧录过程
一、序言 搭建 Jetson 系列产品烧录系统的环境需要在电脑主机上安装 Ubuntu 系统。此处使用 18.04 LTS。 二、环境搭建 1、安装库 $ sudo apt-get install qemu-user-static$ sudo apt-get install python 搭建环境的过程需要这个应用库来将某些 NVIDIA 软件组件安装到 Je…...
