MATLAB:优化与规划问题
一、线性规划



% 线性规划(Linear programming, 简称LP)
fcoff = -[75 120 90 105]; % 目标函数系数向量
A = [9 4 7 54 5 6 105 10 8 53 8 9 77 6 4 8]; % 约束不等式系数矩阵
b = [3600 2900 3000 2800 2200]'; % 约束不等式右端向量
Aeq = []; % 约束等式系数矩阵
beq = []; % 约束等式右端向量
lb = 50*ones(4,1); % 决策变量下限
ub = []; % 决策变量上限
options = optimoptions('linprog','Algorithm','dual-simplex','Display','iter'); % dual-simplex单纯性法
[x,fval,exitflag,output,lambda] = linprog(fcoff,A,b,Aeq,beq,lb,ub,options)
fval = - fval 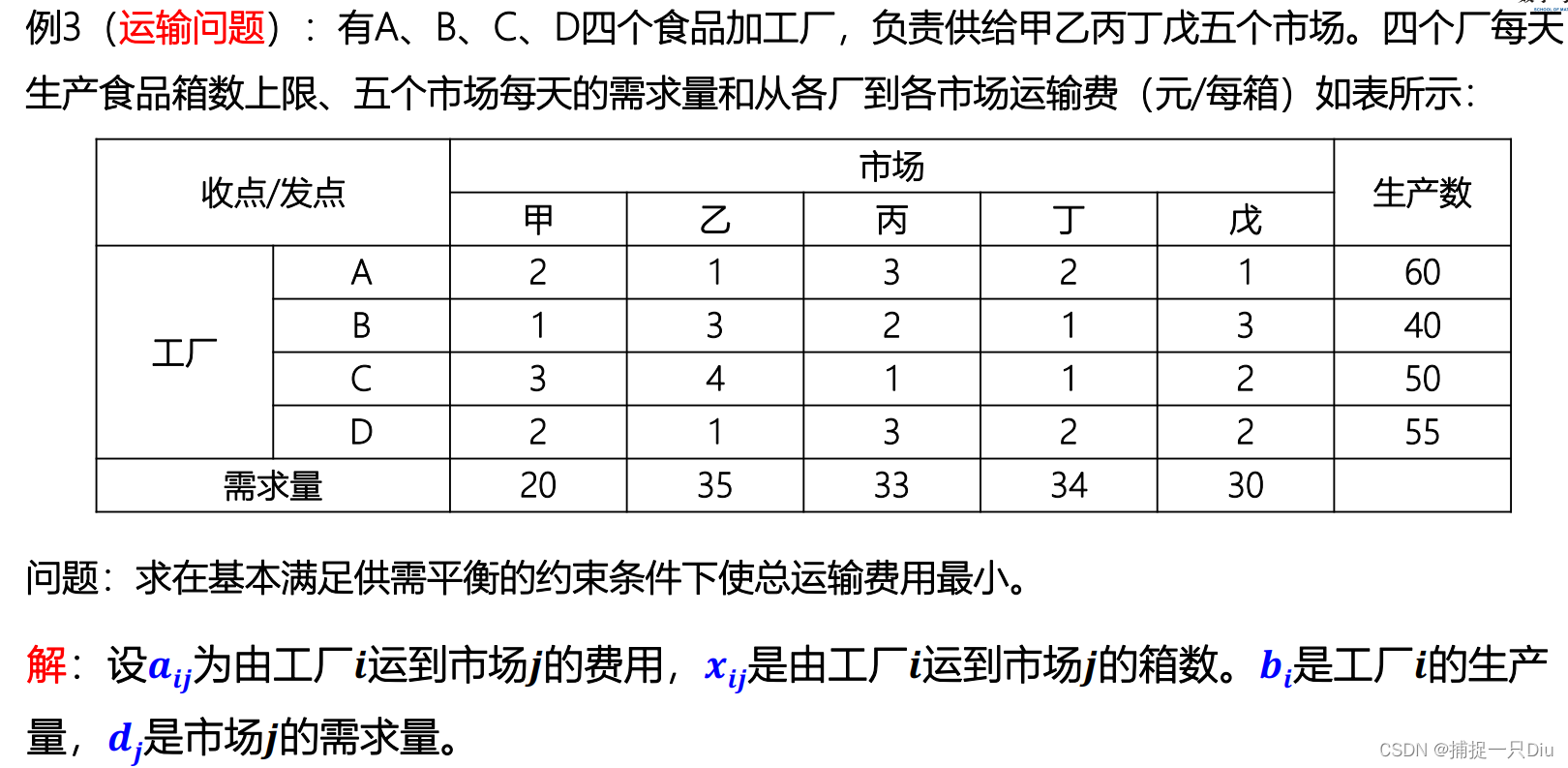

fcoff = [2 1 3 2 1 3 4 1 3 2 1 3 2 1 1 2 1 3 2 2]'; % 按一列一列录入
A = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 00 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 00 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 00 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];
% A1 = repmat(eye(4),1,5)
b = [60 40 50 55]';
Aeq = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
beq = [20 35 33 34 30]';
lb = zeros(20,1);
% options = optimoptions('linprog','Algorithm','interior-point'); % interior-point内点法
options = optimoptions('linprog','Algorithm','dual-simplex'); % dual-simplex单纯性法
[x,fval,exitflag,output,lamda] = linprog(fcoff,A,b,Aeq,beq,lb,[],options)
x = reshape(x,4,5)二、二次规划

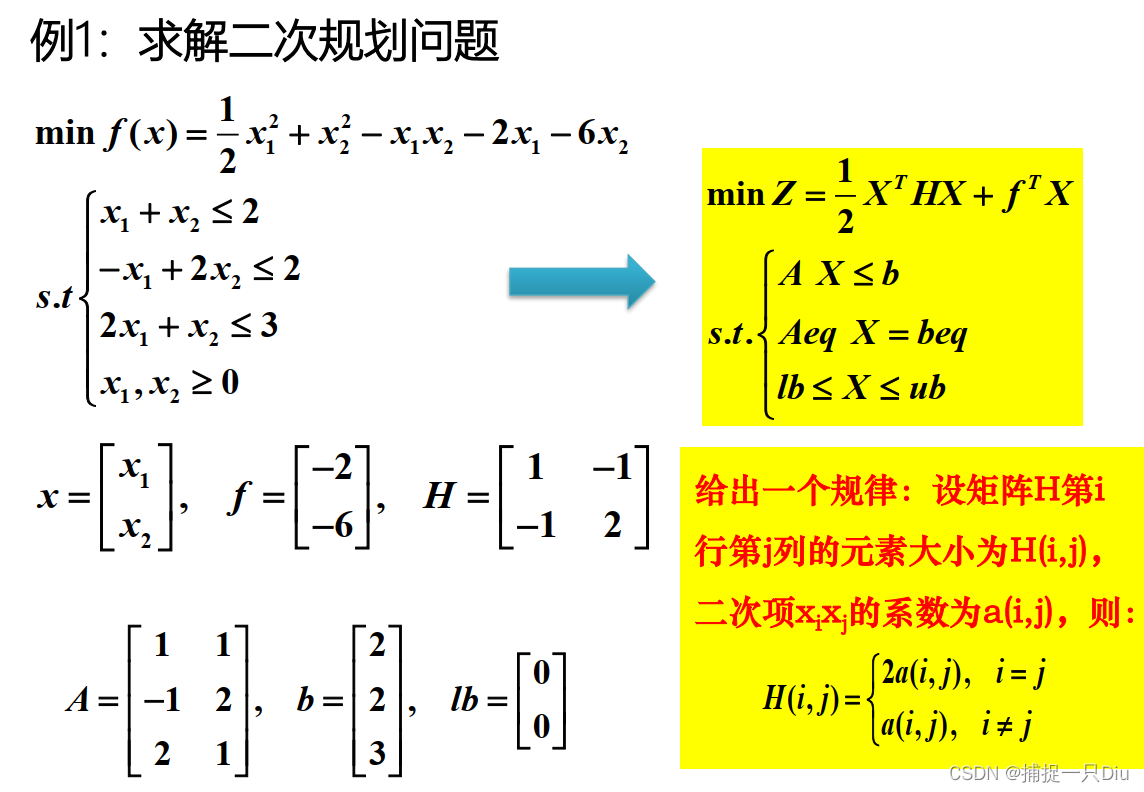
H = [1 -1; -1 2];
f = [-2; -6];
A = [1 1; -1 2; 2 1];
b = [2; 2; 3];
lb = [0; 0];
options = optimoptions('quadprog','Algorithm','interior-point-convex','Display','iter');
[x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb,[],[],options) % 若不加options,则可以省略x0三、混合整数(非)线性规划

intcon: int condition
决策变量0-1问题:
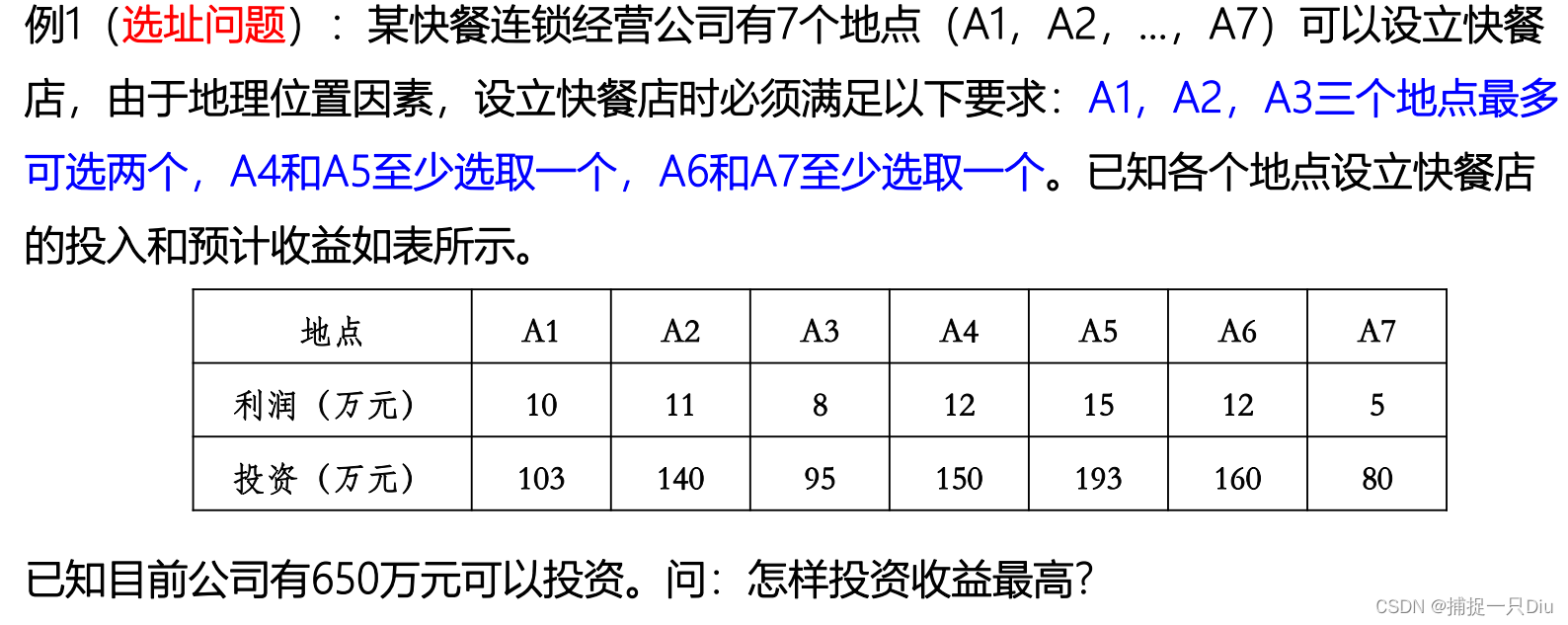

fcoff = [-10 -11 -8 -12 -15 -12 -5];
intcon = 1:7;
A = [103 140 95 150 193 160 80; 1 1 1 0 0 0 0; 0 0 0 -1 -1 0 0; 0 0 0 0 0 -1 -1];
b = [650;2;-1;-1];
Aeq = [];
beq = [];
lb = zeros(7,1);
ub = ones(7,1);
[x,fval,exitflag] = intlinprog(fcoff,intcon,A,b,Aeq,beq,lb,ub)
maxf = -fval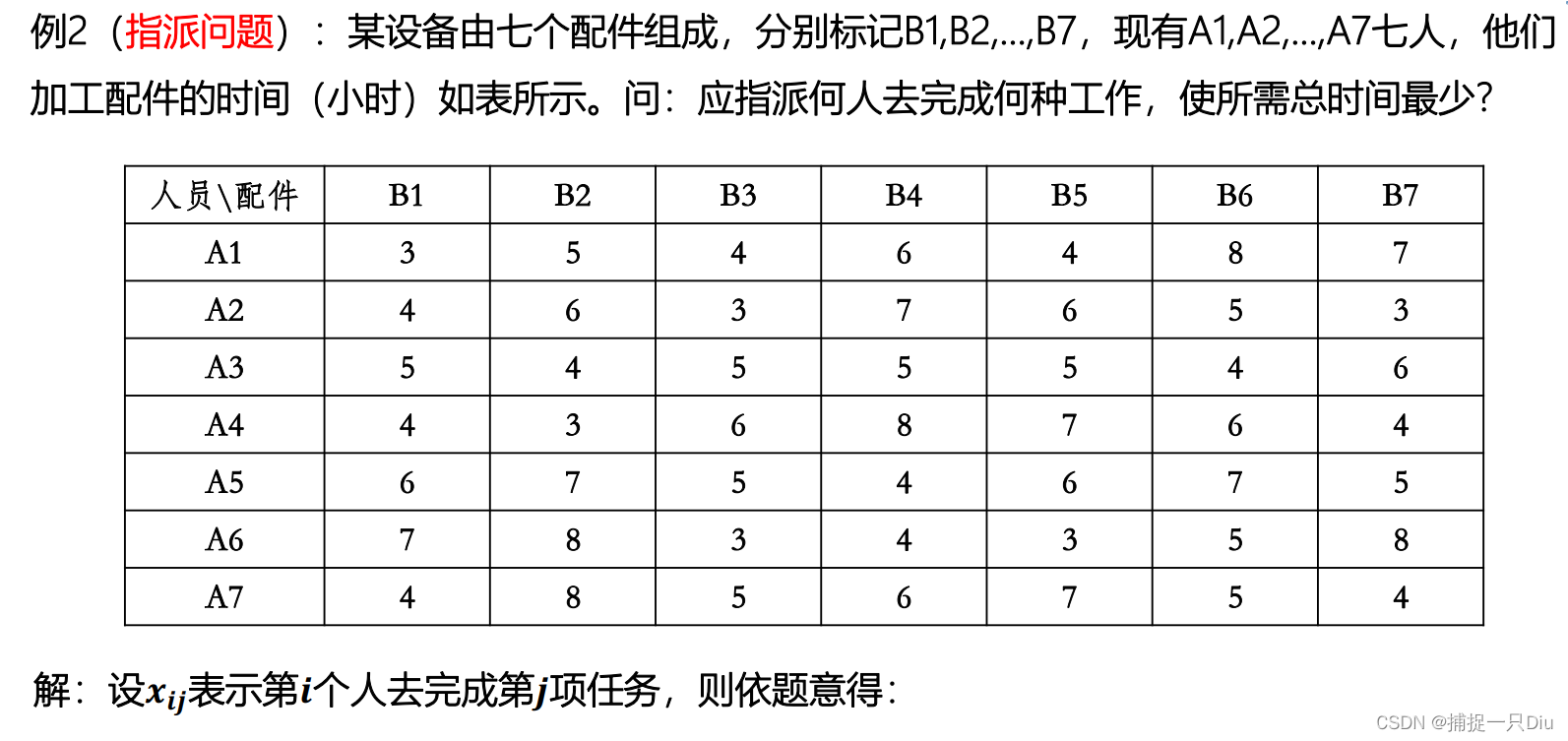

function [x,fval,exitflag] = intlinprog_ex2()designate_data = xlsread('designate.xlsx',1,'B2:H8');fcoff = designate_data(:); % 目标函数系数向量intcon = 1:49;A = [];b = [];Aeq1 = zeros(7,49);for i = 1:7Aeq1(i,(i-1)*7+1:i*7) = 1; % 起点1 8 15 22...,终点7 14 21 28...endAeq2 = repmat(eye(7),1,7);Aeq = [Aeq1;Aeq2];beq = ones(14,1);lb = zeros(49,1);ub = ones(49,1);[x,fval,exitflag] = intlinprog(fcoff,intcon,A,b,Aeq,beq,lb,ub);x = reshape(x,7,7);
end

function [C,Ceq] = stBNB_fun1(x)Ceq = []; % 非线性约束等式% C表示非线性约束不等式C = [x(1)^2 + x(2)^2 + x(3)^2 + x(4)^2 + x(1) - x(2) + x(3) - x(4) - 8;x(1)^2 + 2*x(2)^2 + x(3)^2 + 2*x(4)^2 - x(1) - x(4) - 10;2*x(1)^2 + x(2)^2 + x(3)^2 + 2*x(4)^2 - x(2) - x(4) - 5];
endobjfun = @(x)x(1)^2+x(2)^2+2*x(3)^2+x(4)^2-5*x(1)-5*x(2)-21*x(3)+7*x(4);
x0 = zeros(4,1); % 初值
xstat = ones(4,1); % 都是整数
[errmsg,objval,objX,t,c,fail] = BNB20_new(objfun,x0,xstat,[],[],[],[],[],[],@stBNB_fun1)objfun = @(x)5*x(4)+6*x(5)+8*x(6)+10*x(1)-7*x(3) - 18*log(x(2)+1)-19.2*log(x(1)-x(2)+1)+10;
x0 = zeros(6,1);
xstat = [0 0 0 1 1 1]';
lb = [0 0 0 0 0 0]';
ub = [2 2 1 1 1 1]';
A = [-1 1 0 0 0 0;0 1 0 -2 0 0;1 -1 0 0 -2 0;0 0 0 1 1 0];
b = [0 0 0 1]';
Aeq = [];
beq = [];
[errmsg,objval,objX,t,c,fail] = BNB20_new(objfun,x0,xstat,lb,ub,A,b,Aeq,beq,@stBNB_fun2)四、有约束非线性规划
nonlcon: nonlinear condition
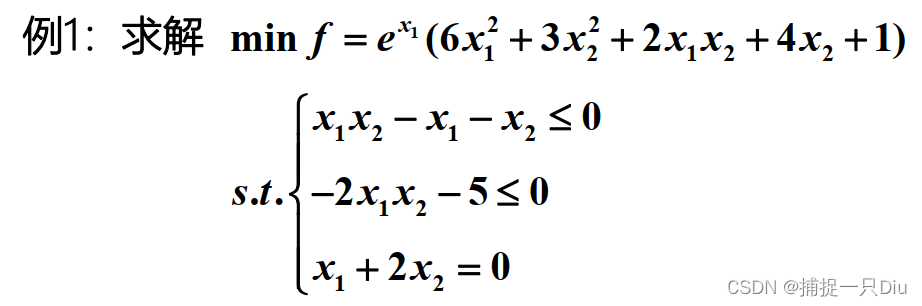
x0 = [-1;0.5];
Aeq = [1,2];
beq = [0];
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point');
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(@objfmincon_1,x0,[],[],Aeq,beq,[],[],@nlincon_fun1,options)

d = [640,850,530,72]; % 目标距离
Ao = (d/2 + d/4 + 200); %飞机携带A炸弹分别摧毁4个目标所需要的油量
Bo = (d/3 + d/4 + 200); %飞机携带B炸弹分别摧毁4个目标所需要的油量
D = [Ao;Bo];
D = D(:)'; % 第一个约束条件的系数行向量
objfun = @(x)(1-0.65)^x(1)*(1-0.76)^x(2)*(1-0.50)^x(3)*(1-0.70)^x(4)*...(1-0.56)^x(5)*(1-0.72)^x(6)*(1-0.68)^x(7)*(1-0.66)^x(8);
x0 = zeros(8,1);
A = [D;1 0 1 0 1 0 1 0;0 1 0 1 0 1 0 1;1 1 0 0 0 0 0 0; 0 0 1 1 0 0 0 0;0 0 0 0 1 1 0 0;0 0 0 0 0 0 1 1;-1 -1 0 0 0 0 0 0; 0 0 -1 -1 0 0 0 0;0 0 0 0 -1 -1 0 0;0 0 0 0 0 0 -1 -1];
b = [2700;4;4;2;2;2;2;-1;-1;-1;-1];
Aeq = [];
beq = [];
lb = zeros(8,1);
ub = [];
nonlcon = [];
options = optimoptions('fmincon','Algorithm','interior-point');
[x,fval,exitflag,output,lambda,grad] = fmincon(objfun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);
x = reshape(x,2,4)
p = 1 - fval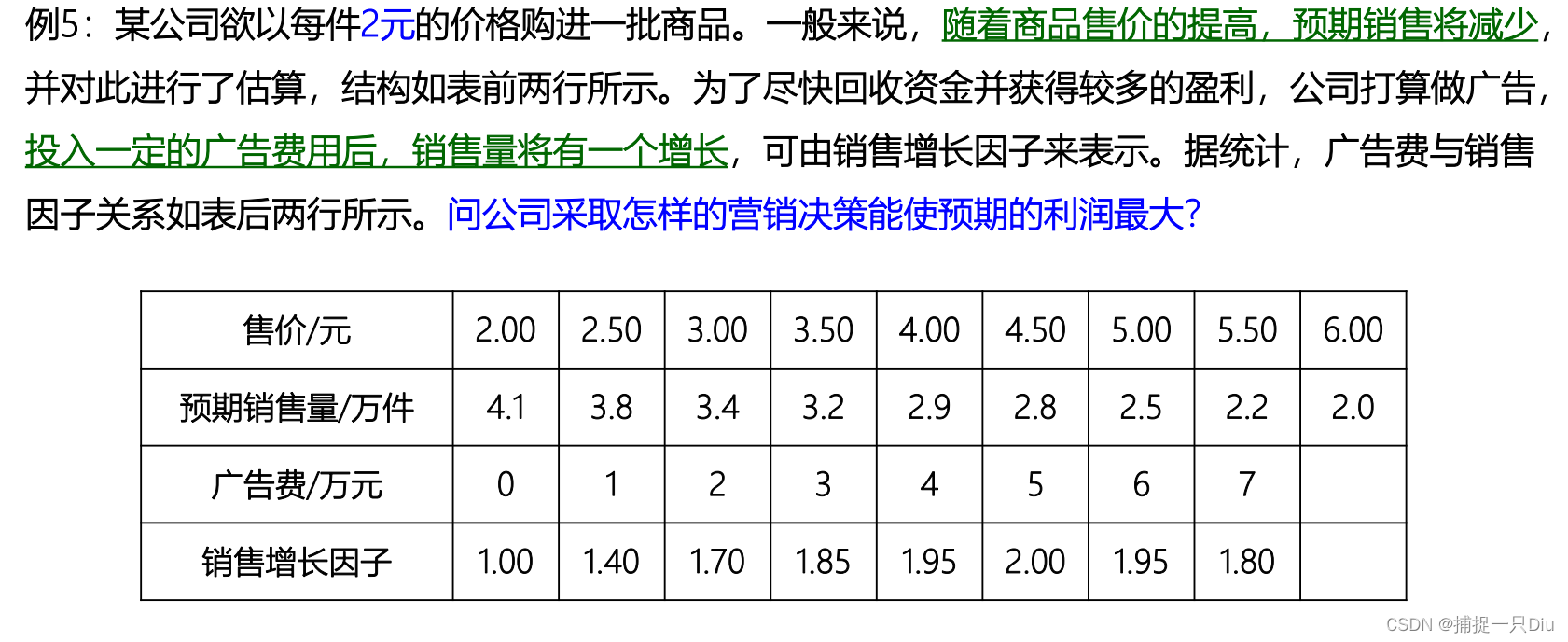
x = [2:0.5:6];
y = [4.1 3.8 3.4 3.2 2.9 2.8 2.5 2.2 2.0];
plot(x,y,'r-*')
grid on
title('售价与预期销售量散点图')
xlabel('售价')
ylabel('预期销售量')
% y = a*x + b
py = polyfit(x,y,1)z = [0:7];
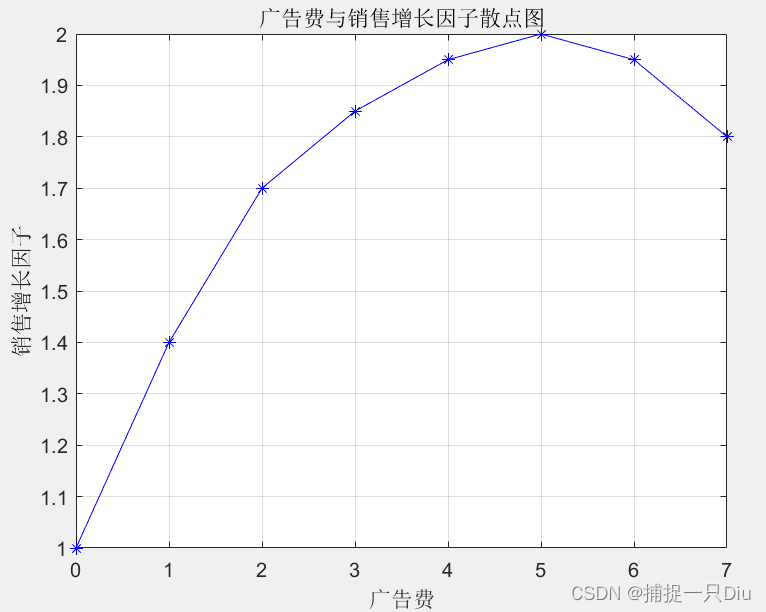
k = [1 1.4 1.7 1.85 1.95 2 1.95 1.8];
figure
plot(z,k,'b-*')
grid on
title('广告费与销售增长因子散点图')
xlabel('广告费')
ylabel('销售增长因子')
% k = c*z^2 + d*z + e
pk = polyfit(z,k,2)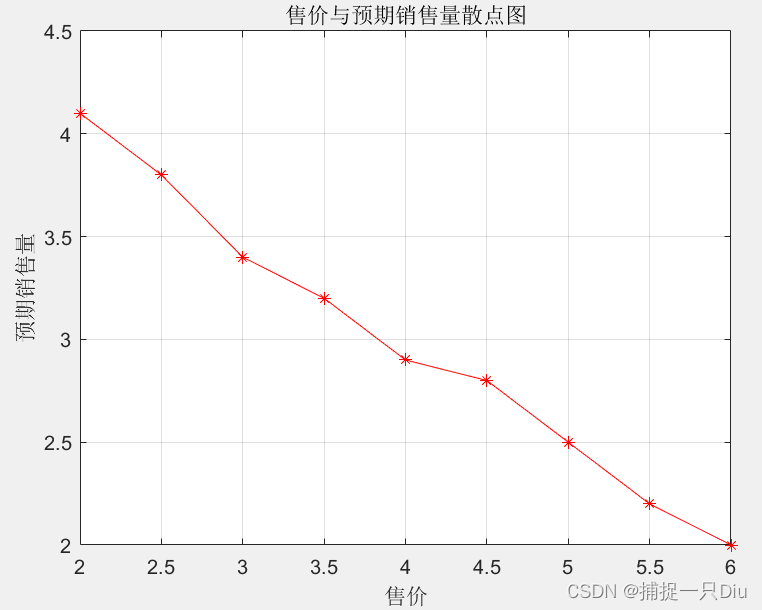

% x(1)-->x, x(2)-->z
objf = @(x)-((py(1)*x(1)+py(2))*(pk(1)*x(2)^2+pk(2)*x(2)+pk(3))*(x(1)-2)-x(2));
lb = [2;0];
x0 = [3;2];
options = optimoptions('fmincon','Algorithm','interior-point');
[x,fval,exitflag,output,lambda,grad] = fmincon(objf,x0,[],[],[],[],lb,[],[],options)五、半无限多元函数约束问题
fseminf
六、多目标规划问题



mobjf = @(x)[[36.9,35.8,24.9,29.9,45.8]*x;[-1,-1,-1,-1,-1]*x]; % 两个目标函数
x0 = ones(5,1);
goal = [1850,-55];
weight = [0.8,0.2];
A = [-1 -1 0 0 00 0 0 -1 -1];
b = [-23;-20];
Aeq = [];
beq = [];
lb = 8*ones(5,1);
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(mobjf,x0,goal,weight,A,b,Aeq,beq,lb)
% attainfactor为达到因子,以实数形式返回。attainfactor 包含解处的 γ 值。
% 如果 attainfactor 为负,则目标过达到
% 如果 attainfactor 为正,则目标欠达到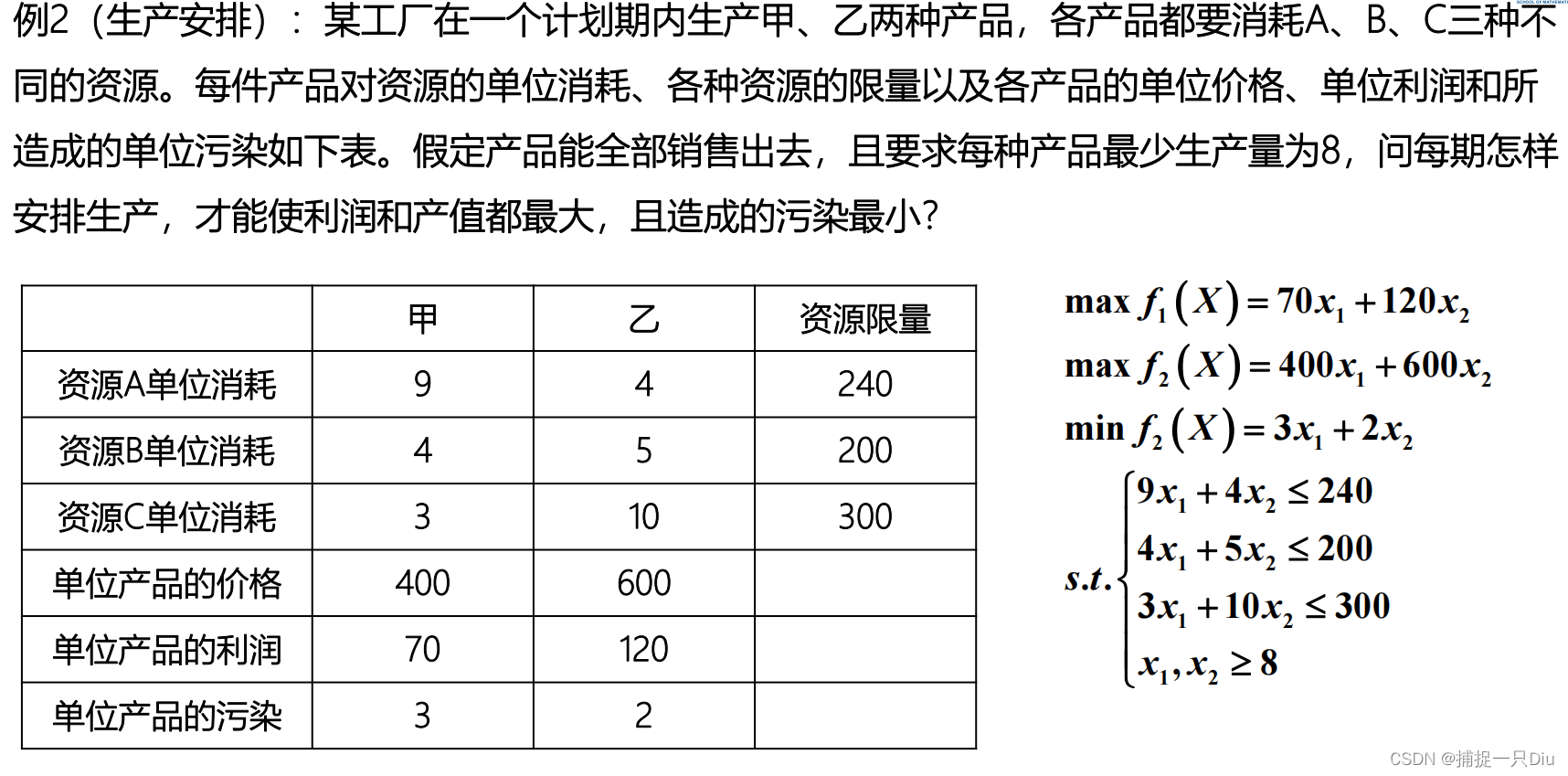
mobjf = @(x)[-[70 120]*x;-[400 600]*x;[3 2]*x];
x0 = ones(2,1);
goal = [-3900,-20000,80];
weight = [0.3 0.3 0.4];
A = [9 4;4 5;3 10];
b = [240;200;300];
lb = [8;8];
[x,fval,attainfactor,exitflag] = fgoalattain(mobjf,x0,goal,weight,A,b,[],[],lb)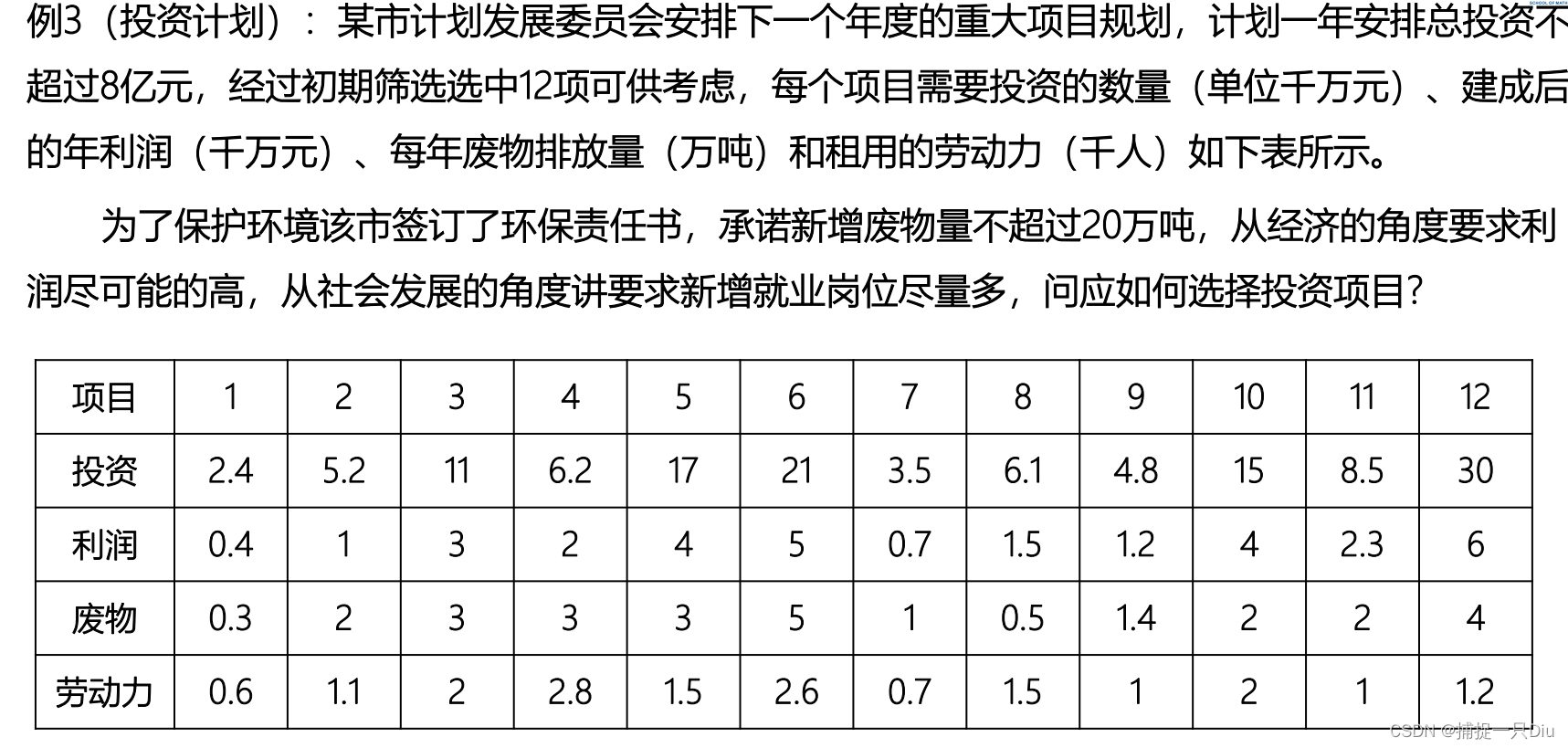

plan = xlsread('planning.xlsx',1,'B2:M5');
invest = plan(1,:); % 投资
profit = plan(2,:); % 利润
waste = plan(3,:); % 废物
labour = plan(4,:); % 劳动力
mobjf = @(x)-[profit*x;labour*x]; % 目标函数,最大值转化为最小值
x0 = zeros(12,1); % 初值选择
lb = zeros(12,1); % 决策变量下限
ub = ones(12,1); % 决策变量上限
goal = -[sum(profit);sum(labour)]; %目标
% goal = -[20.74;14.86]; % 通过线性规划求解在满足约束条件下的目标值
weight = abs(goal); % 权重
A = [invest;waste]; % 线性约束不等式系数矩阵
b = [80;20]; % 线性约束不等式右端向量
options = optimoptions('fgoalattain','Display','iter','MaxIterations',100,'ConstraintTolerance',1e-8);
[x,fval,attainfactor,exitflag,output,lambda] = fgoalattain(mobjf,x0,goal,weight,A,b,[],[],lb,ub,[],options)七、极小化极大问题



nonlcon: 定义非线性等式和不等式
% Minimax一般是寻找一个局部最优解而不是全局最优解
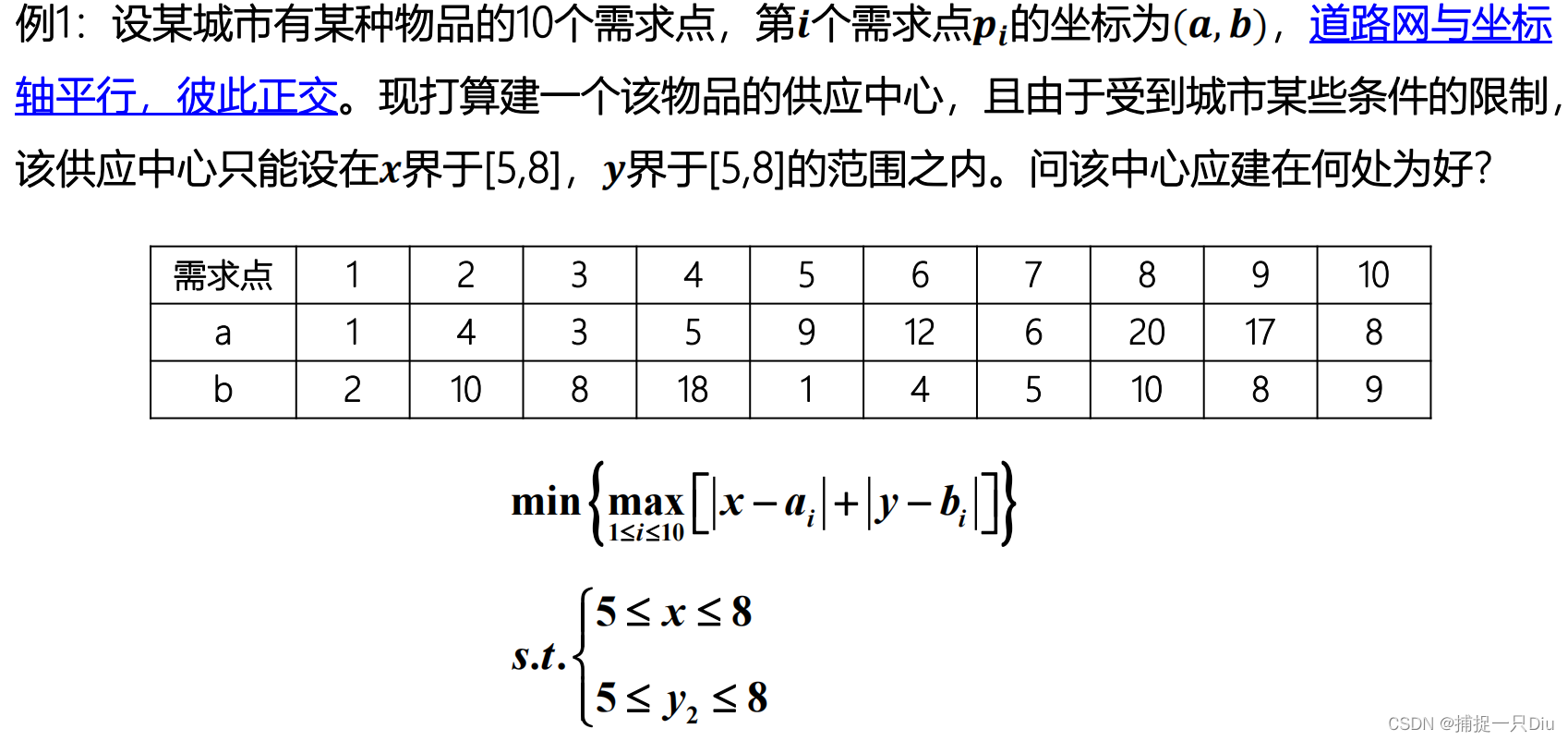
lb = [5;5];
ub = [8;8];
x0 = [1;1];
[x,fval,maxfval,exitflag,output] = fminimax(@fminimax_fun1,x0,[],[],[],[],lb,ub)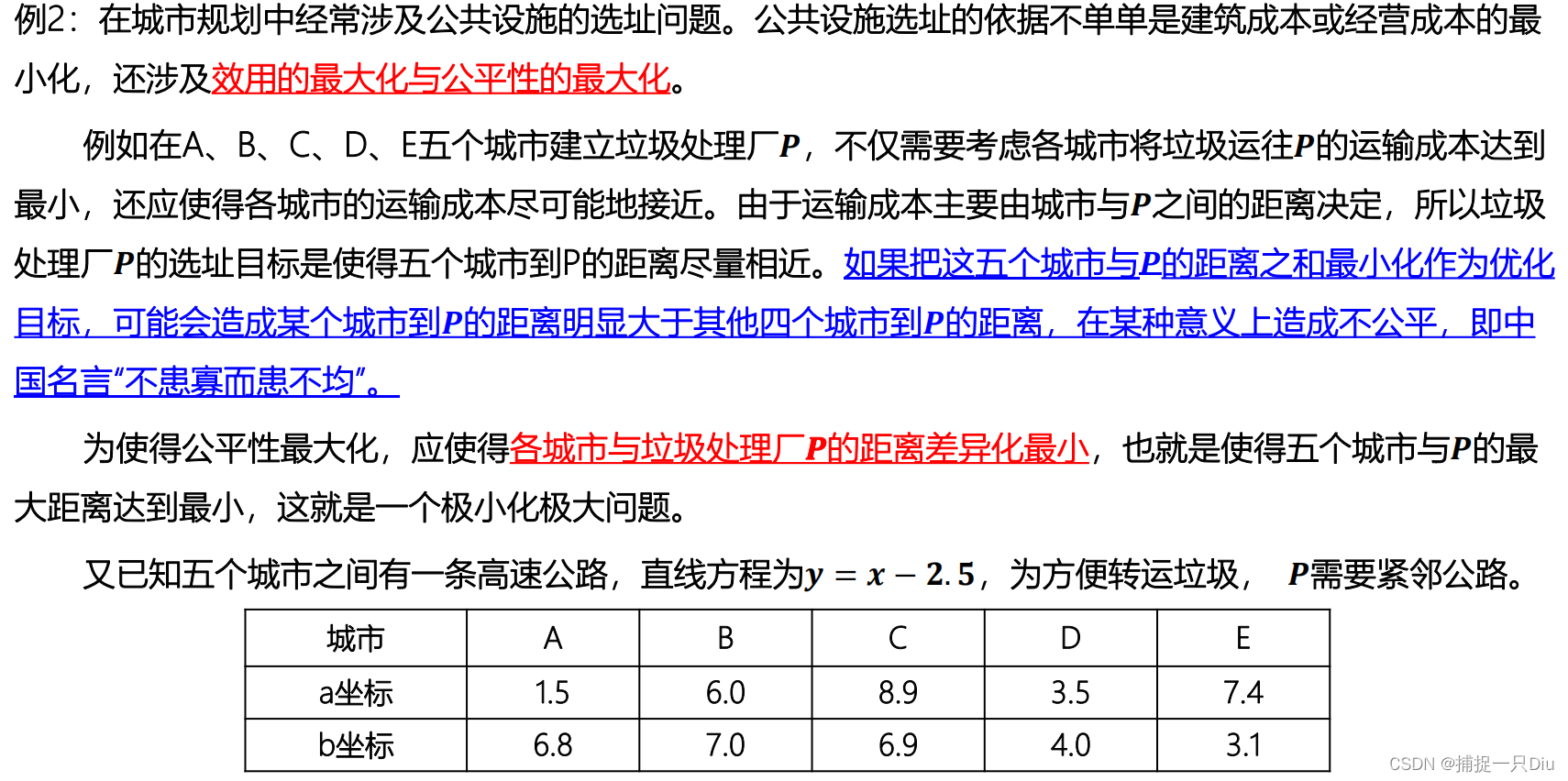

objf = @(x)sqrt([(x(1)-1.5)^2+(x(2)-6.8)^2;(x(1)-6.0)^2+(x(2)-7.0)^2; (x(1)-8.9)^2+(x(2)-6.9)^2;(x(1)-3.5)^2+(x(2)-4.0)^2; (x(1)-7.4)^2+(x(2)-3.1)^2]);
x0 = [0;0];
Aeq = [1 -1];
beq = [2.5];
[x,fval,maxfval,exitflag,output] = fminimax(objf,x0,[],[],Aeq,beq)八、线性约束最小二乘问题
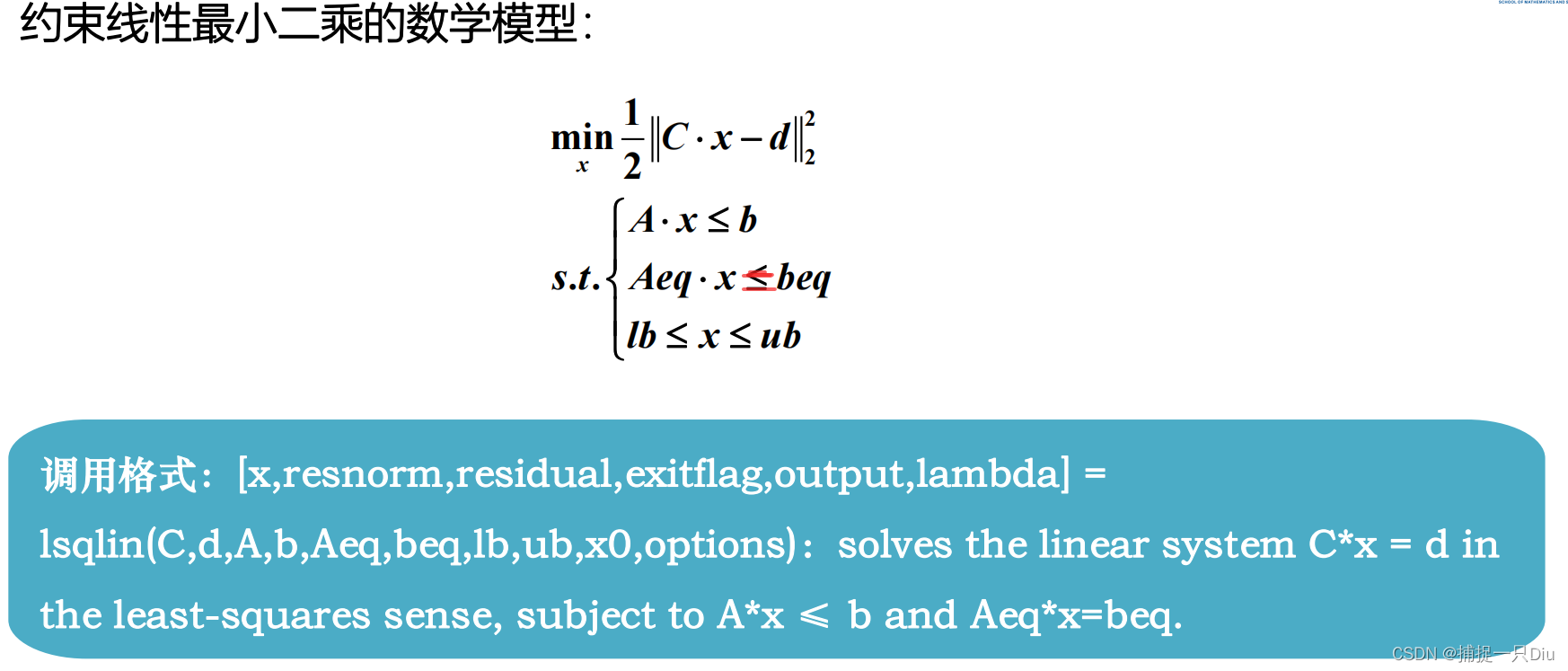
lsqlin: Solve constrained linear least-squares problems.

C = [0.9501 0.7620 0.6153 0.40570.2311 0.4564 0.7919 0.93540.6068 0.0185 0.9218 0.91690.4859 0.8214 0.7382 0.41020.8912 0.4447 0.1762 0.8936];
d = [0.0578 0.3528 0.8131 0.0098 0.1388]';
A = [0.2027 0.2721 0.7467 0.46590.1987 0.1988 0.4450 0.41860.6037 0.0152 0.9318 0.8462];
b = [0.5251 0.2026 0.6721]';
Aeq = [3 5 7 9];
beq = 4;
lb = -0.1*ones(4,1);
ub = 2*ones(4,1);
x0 = rand(4,1);
options = optimoptions('lsqlin','Algorithm','interior-point','Display','iter');
[x,resnorm,residual,exitflag,output,lambda] = lsqlin(C,d,A,b,Aeq,beq,lb,ub,x0,options)九、动态规划
dynprog
十、智能优化算法
1、遗传算法
nonlcon: 定义非线性等式与不等式
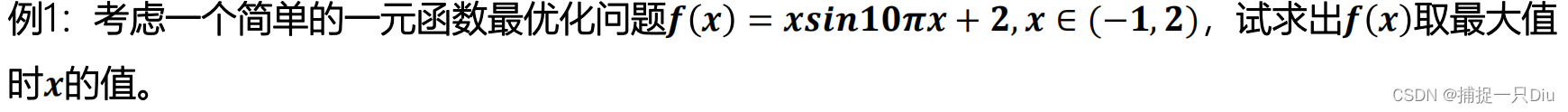
fh = @(x)-(x.*sin(10*pi*x) + 2);
fplot(fh,[-1,2])
% fmincon
v = [];
xi = [-1:0.8:1.5,1.5:0.1:2];
for x0 = xisolx = fmincon(fh,x0,[],[],[],[],-1,2);v = [v;x0,solx,-fh(solx)];
end
options = optimoptions('ga','Display','iter');
[x,fval] = ga(fh,1,[],[],[],[],-1,2,[],options)
fmin = @(x)5*x(4)+6*x(5)+8*x(6)+10*x(1)-7*x(3)-18*log(x(2)+1)-19.2*log(x(1)-x(2)+1)+10;
nvars = 6; % 决策变量的个数
intcon = [4,5,6]; % 取整决策变量下标
ub = [2 2 1 1 1 1]';
lb = [0 0 0 0 0 0]';
A = [-1 1 0 0 0 0;0 1 0 -2 0 0;1 -1 0 0 -2 0;0 0 0 1 1 0];
b = [0 0 0 1]';
options = optimoptions('ga','Display','iter');
[x,fval] = ga(fmin,nvars,A,b,[],[],lb,ub,@gacon_fun1,intcon,options)% 使用三中的BNB20_new函数
objfun = @(x)5*x(4)+6*x(5)+8*x(6)+10*x(1)-7*x(3)-18*log(x(2)+1)-19.2*log(x(1)-x(2)+1)+10;
x0 = zeros(6,1); % 初值
xstat = [0 0 0 1 1 1]'; % 都不是整数
xlb = [0 0 0 0 0 0]';
xub = [2 2 1 1 1 1]';
A = [-1 1 0 0 0 0;0 1 0 -2 0 0;1 -1 0 0 -2 0;0 0 0 1 1 0];
b = [0 0 0 1]';
Aeq = [];
beq = [];
[errmsg,objval,objX,t,c,fail] = BNB20_new(objfun,x0,xstat,xlb,xub,A,b,Aeq,beq,@gacon_fun1)2、粒子群算法

![]()
fh = @(x)-x.*sin(10*pi*x) - 2;
[x,fval,exitflag,output] = particleswarm(fh,1,-1,2)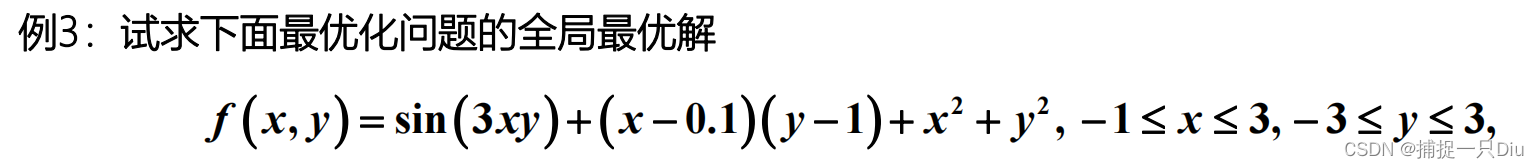
% fh = @(x,y)sin(3*x.*y)+(x-0.1).*(y-1)+x.^2+y.^2;
% fsurf(fh,[-1,3,-3,3])
fh = @(x)sin(3*x(1).*x(2))+(x(1)-0.1).*(x(2)-1)+x(1).^2+x(2).^2;
[x,fval,exitflag,output] = particleswarm(fh,2,[-1;-3],[3;3])3、模拟退火算法
% 测试函数函数dejong5fcn
[x,fval] = simulannealbnd(@dejong5fcn,rand(1,2))![]()
% fh = @(x,y)(20 + x^2 + y^2 - 10*(cos(2*pi*x) + cos(2*pi*y)));
% fsurf(fh)
fh = @(x)(20 + x(1).^2 + x(2).^2 - 10*(cos(2*pi*x(1)) + cos(2*pi*x(2))));
[x,fval,exitflag] = simulannealbnd(fh,rand(1,2))相关文章:

MATLAB:优化与规划问题
一、线性规划 % 线性规划(Linear programming, 简称LP) fcoff -[75 120 90 105]; % 目标函数系数向量 A [9 4 7 54 5 6 105 10 8 53 8 9 77 6 4 8]; % 约束不等式系数矩阵 b [3600 2900 3000 2800 2200]; % 约束不等式右端向量 Aeq []; % 约束等式系…...

Oracal执行计划解析
概述 | Id | Operation | Name | Rows | Bytes | TempSpc | Cost (%CPU) | Time | ----------------------------------------------------------------------------------- | 0 | SELECT STATEMENT | | 1…...
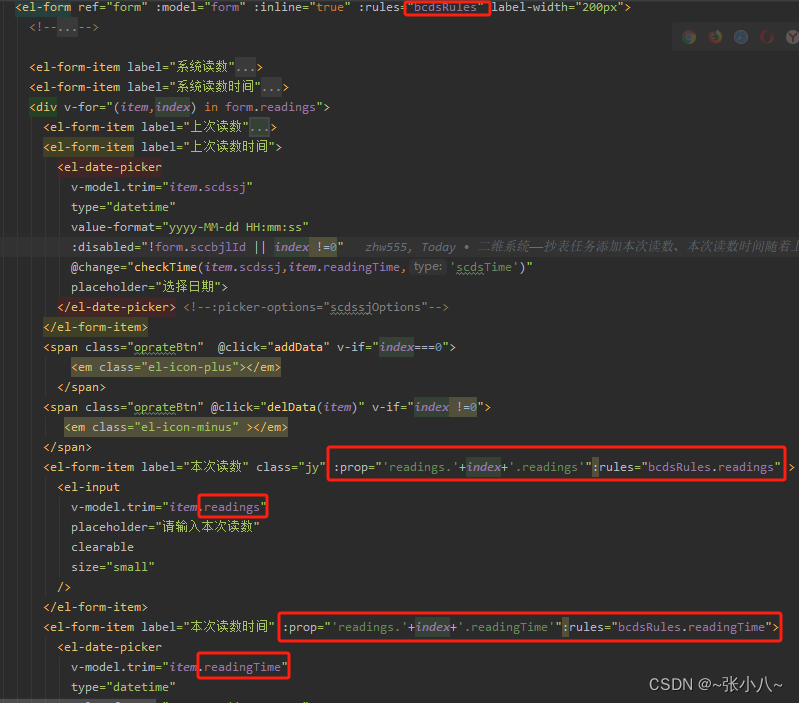
对form表单对象中数组中的字段进行校验的方法
当对form表单中,数组readings中的字段进行校验时,prop和rules绑定要写成动态的,如下代码 <div v-for"(item,index) in form.readings"><el-form-item label"上次读数" > <!--prop"scds"-->…...

一、JAVA集成海康SDK
JAVA集成海康SDK 文章目录 JAVA集成海康SDK前言一、项目依赖 jar1. examples.jar2. 项目依赖 jna.jar,可以通过 maven依赖到。二、集成SDK1.HcNetSdkUtil 海康 SDK封装类2.HCNetSDK3.Linux系统集成SDK三、总结前言 提示:首先去海康官网下载 https://open.hikvision.com/dow…...

PAT 乙级 1031 查验身份证 c语言实现
一个合法的身份证号码由17位地区、日期编号和顺序编号加1位校验码组成。校验码的计算规则如下: 首先对前17位数字加权求和,权重分配为:{7,9,10,5,8,4,2,1&am…...

LeetCode 345. 反转字符串中的元音字母
给你一个字符串 s ,仅反转字符串中的所有元音字母,并返回结果字符串。 元音字母包括 ‘a’、‘e’、‘i’、‘o’、‘u’,且可能以大小写两种形式出现不止一次。 示例 1: 输入:s “hello” 输出:“holl…...

go中函数与方法的区别与go中关于面向对象理解
声明方法的区别 函数是一段可以独立调用的代码块,它可以有参数和返回值。函数的声明不依赖于任何类型,可以直接通过函数名进行调用。 函数的声明格式如下: func functionName(parameters) returnType {// 函数体 }示例: func A…...
SQL Server 实验二:数据库视图的创建和使用
目录 第一关 相关知识 什么是表 操作数据表 创建数据表 插入数据 修改表结构 删除数据表 编程要求 第一关实验代码: 第二关 相关知识 视图是什么 视图的优缺点 视图的优点 视图的缺点 操作视图 创建视图 通过视图向基本表中插入数据 通过视图修改基本表的…...

树结构导入
Testpublic void testExcel1() {// 写法1:JDK8 ,不用额外写一个DemoDataListener// since: 3.0.0-beta1EasyExcelFactory.read(new File("C:\\Users\\Admin\\Desktop\\树导入.xlsx"), null, new ReadListener<Map>() {public static final int BATC…...

Promise封装ajax
Promise封装原生ajax 1.node的内置模块url, http 2.Promise封装原生ajax 01-node的内置模块 # url: 操作网址 let url require(url) url.parse(网址, [布尔值: 决定是否将查询字符串转换为对象格式]): 将网址解析成对象# http: 创建本地服务器 let http requi…...
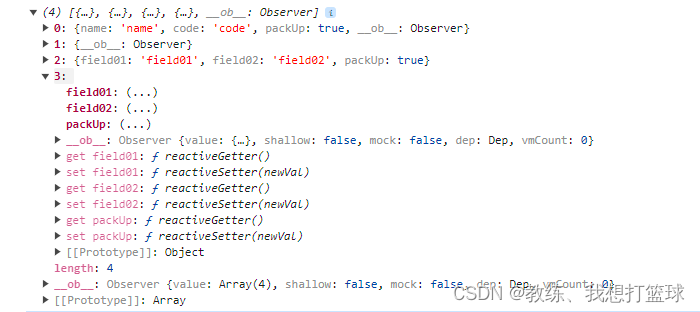
47 vue 常见的几种模型视图不同步的问题
前言 这里主要是来看一下 关于 vue 中的一些场景下面 可能会出现 模型和视图 不同步更新的情况 然后 这种情况主要是 vue 中的对象 属性没有响应式的 setter, getter 然后 我们这里就来看一下 大多数的情况下的一个场景, 和一些处理方式 当然 处理方式主要是基于 Vue.set, …...
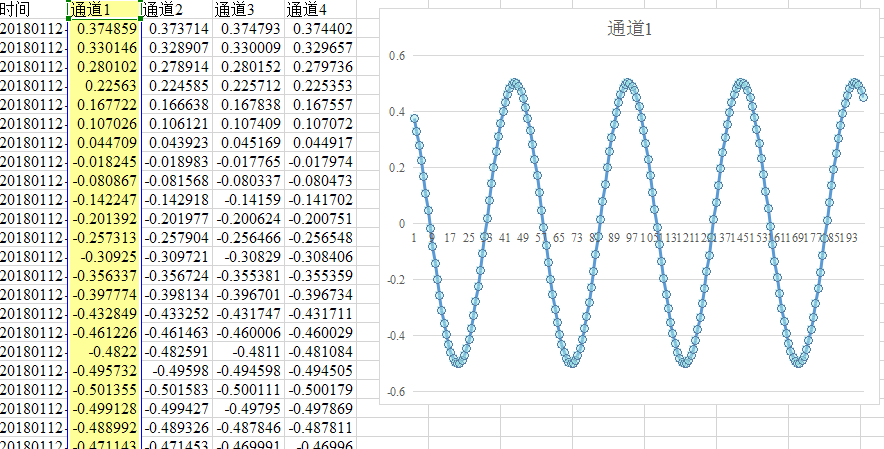
以太网/USB 数据采集卡 24位16通道 labview 256K同步采样
XM7016以太网SUB数据采集卡 XM7016是一款以太网/USB高速数据采集卡,具有16通道真差分输入,24位分辨率,单通道最高采样率256ksps. 16通道同步共计4.096Msps、精密前置增益放大、集成IEPE/ICP硬件支持的特点。本产品采用了多个高精度24位ADC单元…...

python基础 | 核心库:PIL
1、读取图像信息 查看图像信息 读取同一文件夹下的文件 可加 ./可不加 rom PIL import Image img Image.open(image.jpg) # 打开图像文件(注意:是去掉文件头的纯数据) print(img.format) # 图像格式(如BMP PNG JPEG 等) print(img.size) # 图像大小(…...
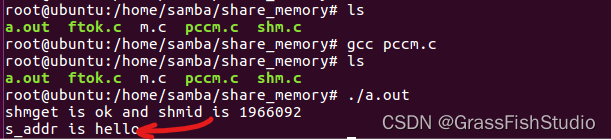
#Linux系统编程(共享内存)
(一)发行版:Ubuntu16.04.7 (二)记录: (1)什么是共享内存 共享内存是System V版本的最后一个进程间通信方式。共享内存,顾名思义就是允许两个不相关的进程访问同一个逻辑…...

蓝桥杯备考随手记: practise01
问题描述: 小明对数位中含有 2、0、1、9 的数字很感兴趣,在 1 到 40 中这样的数包 括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574。 请问,在 1 到 2019 中,所有这样的数的和是多少? 思路分析…...

【openGL4.x手册09】转换反馈
目录 一、说明二、着色器设置2.2 捕获的数据格式2.2 高级交错2.3 双精度和对齐2.4 In-shader规范 三、缓冲区绑定四、反馈过程五、反馈对象5.1 反馈暂停和恢复5.2 绑定暂停的反馈对象。 六、反馈渲染七、局限性 一、说明 转换反馈是捕获由顶点处理步骤生成的基元的过程…...

记录一次报错提示npx update-browserslist-db@latest
1,定位文件夹位置 找到HBuilderX的安装目录, cmd切换到HBuilderX/plugins/uniapp-cli下 删除node_modules以及package-lock.json 在当前目录执行npm install 重新打开HBuilderX运行 2, 删除后,再次通过hbuilderX启动微信小程序,会…...
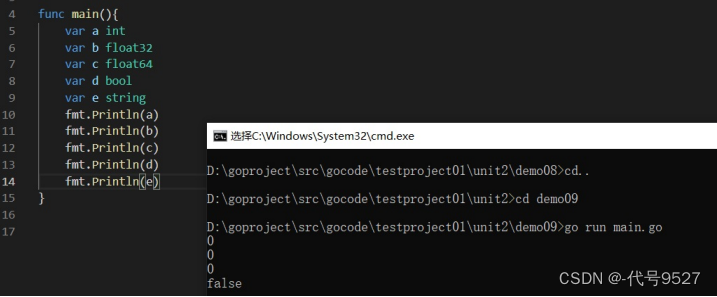
【Go】二、Go的基本数据类型
文章目录 0、进制1、变量的声明2、数据类型3、整型4、浮点型5、字符类型6、布尔类型7、字符串类型8、基本数据类型的默认值9、类型转换10、基本类型转String11、String转其他类型 0、进制 N进制,逢N进一 1、变量的声明 //声明 赋值 var age int 18//声明、赋值、…...

十一、Spring源码学习之registerListeners方法
registerListeners()方法 protected void registerListeners() {// Register statically specified listeners first.//获取容器中事件监听并存放到多播器中 applicationListenersfor (ApplicationListener<?> listener : getApplicationListeners()) {getApplicationE…...

Oracle 控制文件详解
1、控制文件存储的数据信息 1)数据库名称和数据库唯一标识符(DBID) 2)创建数据库的时间戳 3)有关数据文件、联机重做日志文件、归档重做日志文件的信息 4)表空间信息 5)检查点信息 6)日志序列号…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

Python训练营-Day26-函数专题1:函数定义与参数
题目1:计算圆的面积 任务: 编写一个名为 calculate_circle_area 的函数,该函数接收圆的半径 radius 作为参数,并返回圆的面积。圆的面积 π * radius (可以使用 math.pi 作为 π 的值)要求:函数接收一个位置参数 radi…...