图论最短路径以及floyd算法的MATLAB实现
图论是数学的一个分支,起源于18世纪。1736年,数学家欧拉通过解决“哥尼斯堡七桥问题”,将问题抽象成点和线的关系,并通过理论分析得出结论,这个过程标志着图论的产生,欧拉也因此被称为“图论之父”。图论研究的是由若干给定的点及连接两点的线所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,其中点代表事物,连接两点的线表示相应两个事物间具有这种关系。
一、无向图和有向图在图论中都是重要的概念,它们之间存在显著的区别。
首先,从定义上来看,无向图是一种由节点和边组成的数据结构,边没有方向性,也就是说,如果存在一条边(u, v),那么从u到v和从v到u都是可以的。这种图通常用来表示双向关系,如社交网络中的友谊关系。而有向图则是一种具有方向性的图,由一组顶点和一组有方向的边组成,每条方向的边都连着一对有序的顶点。在有向图中,如果存在一条边(u, v),那么只能从u到v,但不一定能从v到u。
此外,从应用角度来看,无向图主要用于表示双向关系,如社交网络、传输网络等,以及用于搜索最短路径等问题。而有向图则更多地用于表示具有方向性的关系,如流程、路径规划等。
二、在图论中,最短路径问题是一个经典问题,它涉及从图中某一顶点(源点)出发,到达另一顶点(终点)的所有路径中,寻找各边权值之和最小的路径,这种路径称为最短路径。
最短路径问题可以分为两类:单源最短路径问题和多源最短路径问题。单源最短路径问题是求单个顶点和其他所有顶点的最短路径,而多源最短路径问题则是求所有顶点相互之间的最短路径。对于最短路径问题,有多种算法可以用来求解,包括但不限于:
- Dijkstra算法:这是最短路径算法中最常用的一种。它基于贪心策略,通过逐步扩展路径来求解最短路径。算法的基本思想是,从一个起始顶点开始,逐步扩展到其他顶点,每次选择当前路径中距离起始顶点最近的顶点进行扩展,直到扩展到目标顶点或者所有顶点都被扩展完毕。
- Bellman-Ford算法:这也是另一种常用的最短路径算法。
- Floyd-Warshall算法:这是一种多源最短路径算法,可以求解图中任意两个顶点之间的最短路径。
以下面问题为例解决问题:

clear;clc;
% 注意Matlab中的图节点要从1开始编号
s = {'v1','v1','v1','v2','v3','v3','v4','v5','v5','v5','v5','v6','v6','v7','v9','v9'};
t = {'v2','v3','v4','v5','v2','v4','v6','v4','v6','v7','v8','v5','v7','v8','v5','v8'};
weight = [6,3,1,1,2,2,10,6,4,3,6,10,2,4,2,3];
%要做出有向图,只需要将graph改为digraph就行了
G= digraph(s,t,weight);%有向图
myplot = plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);%图赋给一个变量
set(gca,'XTick',[],'YTick',[]);
%[p,d] = shortestpath(G,start,end,[‘Method’,algorithm])
% 功能:返回图G中start节点到end节点的最短路径%输入参数:
% (1)G- 输入图 (graph 对象|digraph 对象)
% (2) start 起始的节点%
% (3) end 目标的节点
% (4)[‘Method’,algorithm]是可选的参数,表示计算最短路径的算法。一般我% 们不用手动设置,默认使用的是“auto”,具体可设置的参数见下一页课件。% 输出参数:
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
% (1)P - 最短路径经过的节点
% (2)d - 最短距离
[P,d] = shortestpath(G,'v1','v8')%求v1到v8的最短路径和距离
%在图中高亮出最短路径
highlight(myplot,P,'EdgeColor','red')
%任意两点的最短路径矩阵
D = distances(G)
D(1,8)%v1到v8的最短路径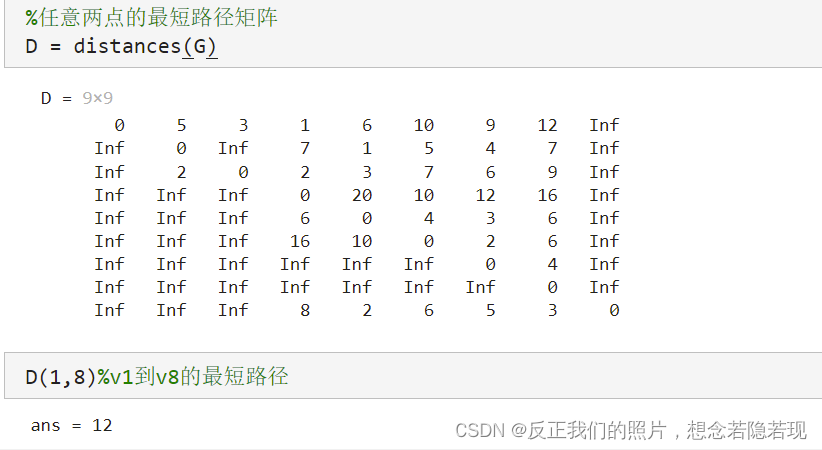 下面是代码floyd算法的MATLAB实现:
下面是代码floyd算法的MATLAB实现:
gg = [0,inf,-2,inf;inf,0,inf,-1; inf,2,0,inf;4,inf,3,0;];
[dist,path] = my_floyd(gg)
function [dist,path] = my_floyd(D)
[r,~]= size(D);
dist = D;
% 下面我们来初始化path矩阵
path = zeros(r);
for j= 1:rpath(:,j) = j; %将第j列的元素变为j
end
for i = 1:rpath(i,i) = -1;%将主对角线元素变为-1
end
for k=1:r%以k为中转for i=1:r %邻接矩阵第i行for j=1:r%邻接矩阵第j列if dist(i,j)>dist(i,k)+dist(k,j)dist(i,j)=dist(i,k)+dist(k,j);path(i,j)=path(i,k);% 起点为i,终点为j的两个节点之间的最短路径要经过的节点更新为path(i,k)% 注意,上面一行语句不能写成path(i,j) = k;endendend
end
end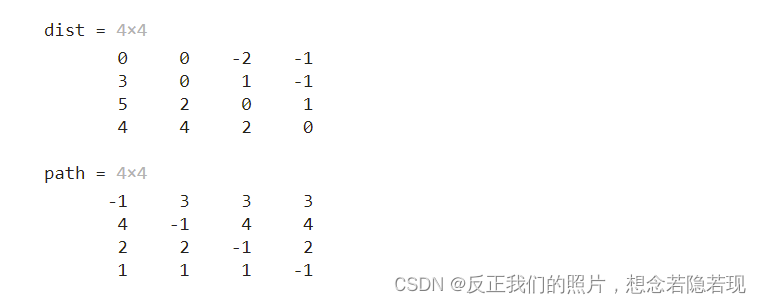 总的来说,图论是一门研究图与网络的理论学科,它在各个领域都发挥着重要的作用,为解决实际问题提供了有力的工具和方法。
总的来说,图论是一门研究图与网络的理论学科,它在各个领域都发挥着重要的作用,为解决实际问题提供了有力的工具和方法。
相关文章:

图论最短路径以及floyd算法的MATLAB实现
图论是数学的一个分支,起源于18世纪。1736年,数学家欧拉通过解决“哥尼斯堡七桥问题”,将问题抽象成点和线的关系,并通过理论分析得出结论,这个过程标志着图论的产生,欧拉也因此被称为“图论之父”。图论研…...
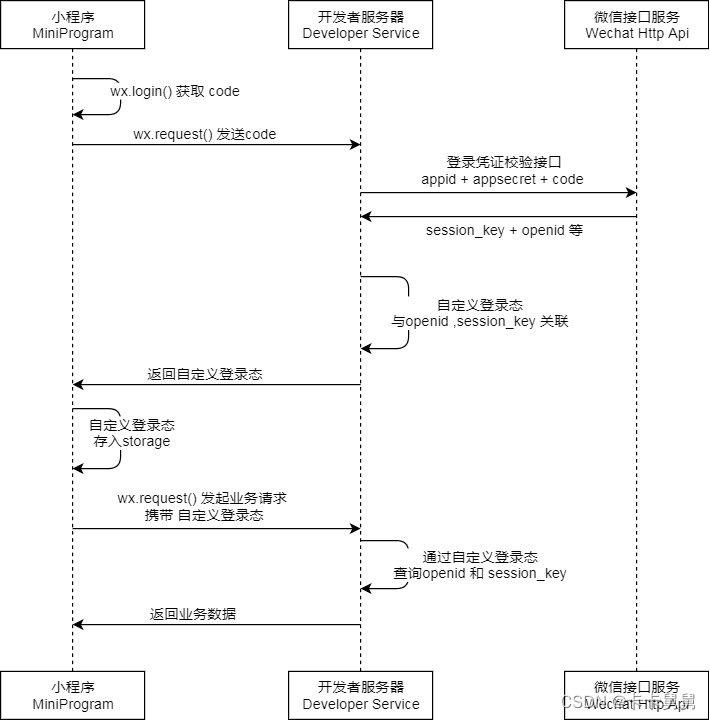
微信小程序 - 登录功能实现
一、认证流程 1. 小程序调用wx.login获取登录认证需要的code,并请求开发者服务器。 2. 开发者服务器根据code,appid, appsecret请求微信接口t获取 openid与session_key ,并生成自己的认证token,并返回给小程序。 3.小程序请求开…...

Python连接MySQL
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、整体思路二、连接流程三、表结构及代码实现 一、整体思路 二、连接流程 三、表结构及代码实现 代码块如下: import pymysqlcon pymysql.connect(h…...

水泊梁山108小酒坛之呼保义宋江
宋江【绰号呼保义、及时雨】字公明,是古典名著《水浒传》中的角色。原为山东郓城县押司,他和晁盖互通往来的事被阎婆惜发现,因此怒杀阎婆惜,逃回家隐藏。后前往清风寨投靠花荣,却被清风寨观灯时遭知寨刘高之妻陷害入狱…...

java.lang.ClassNotFoundException: javafx.application.Application
java8(jdk1.8)到java10(jdk10)中内含有JavaFx 在java11(jdk11)以及以后的版本中剥离出来需要开发者独立下载,另行导入download https://gluonhq.com/products/javafx/java --module-path $FX-P…...
腾讯 tendis 替代 redis linux安装使用
下载地址 Tendis存储版 点击下载 linux 解压 tar -zxvf 安装包.tgz cd 解压安装包/scripts 启动 ./start.sh 停止 ./stop.sh 详细配置 修改 /scripts tendisplus.conf # tendisplus configuration for testing # 绑定本机IIP bind 192.168.31.112 port 51002 #设…...

k8s调优--来自gpt
Kubernetes(K8s)性能调优是一个涉及多个方面的过程,旨在提高集群的效率和响应速度。这包括对节点、Pod、服务、网络和存储等多个层面进行调优。下面我将概述一些常见的Kubernetes性能调优方法: 节点级别的调优: 1.资源分配&…...
HTML5+CSS3小实例:旋转中的视差效果
实例:旋转中的视差效果 技术栈:HTML+CSS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"> <head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scal…...

3-zookeeper之ZAB协议
Zookeeper ZAB协议 概述 ZAB(Zookeeper Automic Broadcast)是一套专门为Zookeeper设计的用于进行原子广播和崩溃恢复的协议ZAB协议主要包含了两个功能 原子广播:保证数据一致性崩溃恢复:保证集群的高可用 ZAB协议本身是基于2PC算法来进行的设计&#…...

如何为企业策划一场XR虚拟直播?
活动年年办,都是老一套,想玩点新花样? 预算有限,但还是想把活动办的逼格高一点? 想通过活动,让更多的人知道自己企业的品牌? 随着AIGC技术的不断演变,企业活动的形式和内容也在不…...

6.3物联网RK3399项目开发实录-驱动开发之I2C 使用(wulianjishu666)
物联网开发源码案例集: 链接:https://pan.baidu.com/s/1kfPDpYZpm_G0GBLAup3KTQ?pwdvgvv I2C 使用 简介 AIO-3399J 开发板上有 9 个片上 I2C 控制器,各个 I2C 的使用情况如下表: 本文主要描述如何在该开发板上配置 I2C。 配置…...

HarmonyOS实战开发-如何构建多种样式弹窗
介绍 本篇Codelab将介绍如何使用弹窗功能,实现四种类型弹窗。分别是:警告弹窗、自定义弹窗、日期滑动选择器弹窗、文本滑动选择器弹窗。需要完成以下功能: 点击左上角返回按钮展示警告弹窗。点击出生日期展示日期滑动选择器弹窗。点击性别展…...

《Effective C++》《构造/析构/赋值运算——7、为多态基类声明virtual析构函数》
文章目录 1、term7:Declare destructors virtual in polymorphic base classes2、总结3、相关面试题3.1 析构函数在什么情况下声明为虚函数 4、参考 1、term7:Declare destructors virtual in polymorphic base classes 带有多态性质的基类应该声明一个virtual析构函数&#x…...

Type-C一分二快充线智能分配方案
随着移动设备的普及和快充技术的迅猛发展,Type-C接口已成为众多手机、平板和笔记本电脑的标配。然而,在日常使用中,我们经常会遇到需要同时为多个设备充电的情况。这时,Type-C一分二快充线就显得尤为重要。为了更好地满足用户的充…...
)
利用python脚本,根据词条爬取百度图片(爬虫)
把广角,换成你的关键词就行 # -*- coding: utf-8 -*- """ Created on Wed Mar 29 10:17:50 2023 author: MatpyMaster """ import requests import os import redef get_images_from_baidu(keyword, page_num, save_dir):header {Us…...
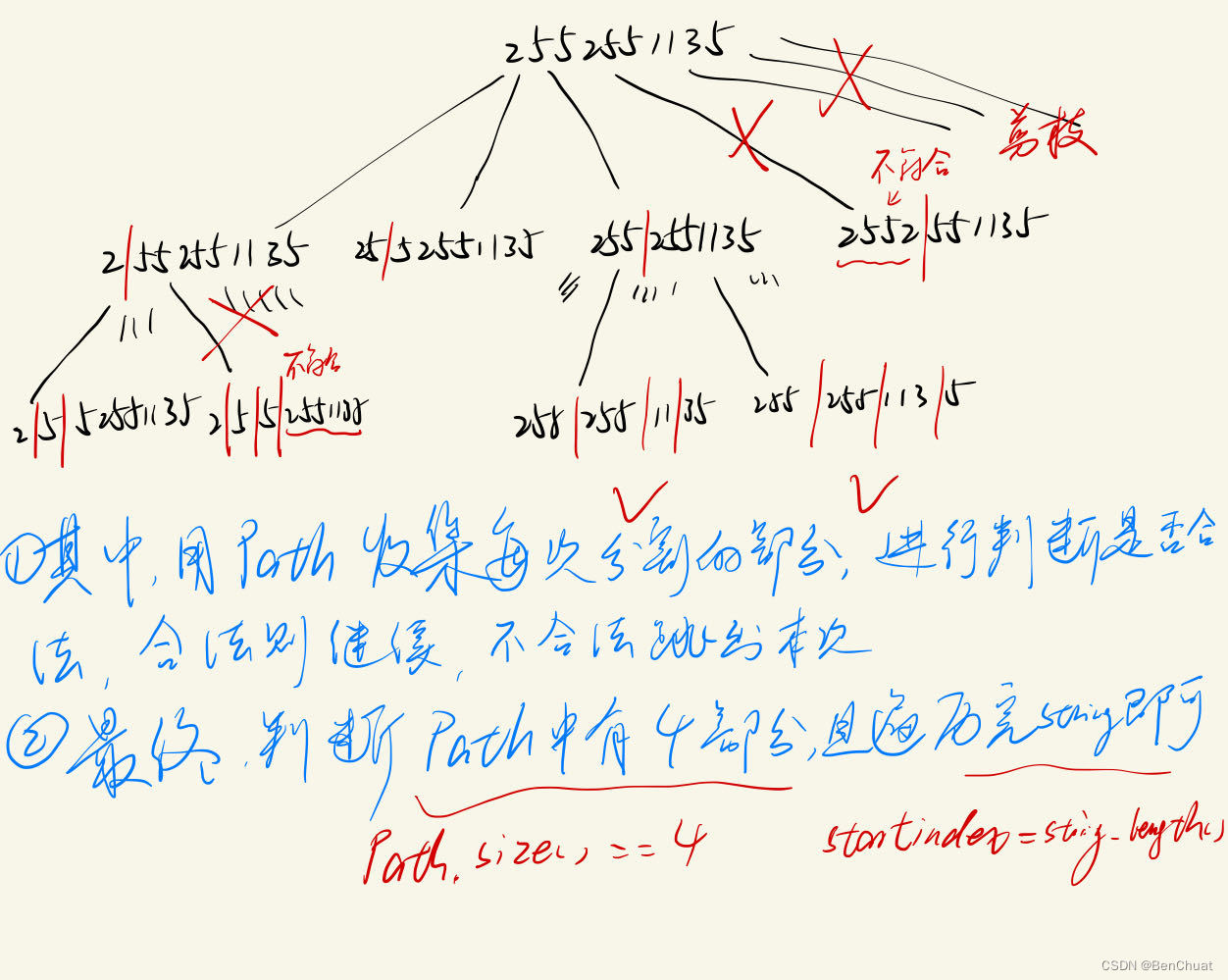
java复原IP 地址(力扣Leetcode93)
复原IP 地址 力扣原题链接 问题描述 有效 IP 地址正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。 例如:“0.1.2.201” 和 “192.168.1.1” 是有效 IP 地址,…...

k8s的创建资源的流程图
背景 在k8s中创建资源需要经过几个流程的协作,包括认证模块,授权模块和资源管理模块的共同处理的结果 k8s的创建资源的流程图 第一步认证模块: k8s需要确保操作的客户端是合法的用户,并且不是仿冒的,也就是判断这个u…...
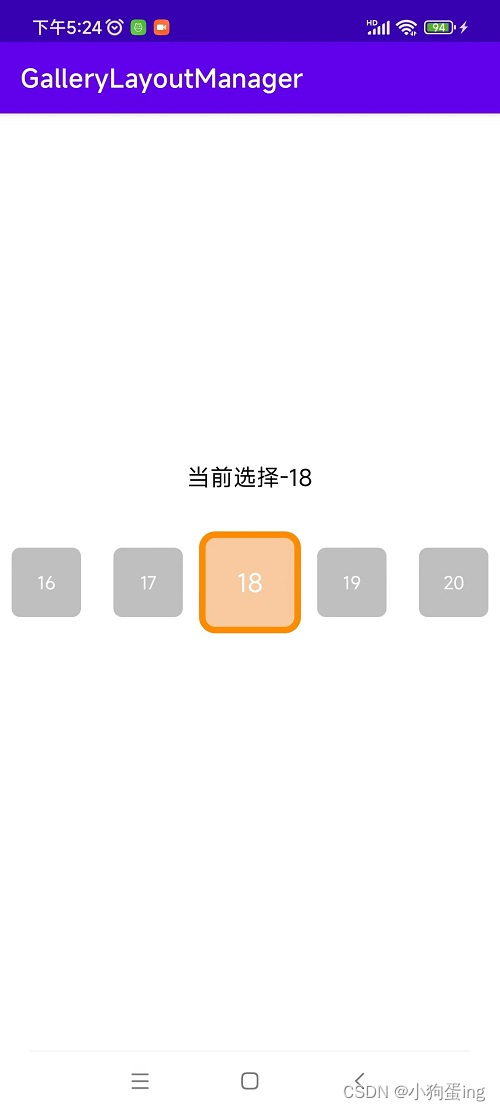
Android RecyclerView 滑动后选中的条目居中显示
话不多说先看效果: 实录效果视频如下 滚动居中 RecyclerView 在原有的RecyclerView 基础上操作,其他步骤不变,只是替换一下 manager 步骤 导入依赖 maven { url https://www.jitpack.io }//无限滚动implementation com.github.ZhaoChanghu:GalleryLayou…...
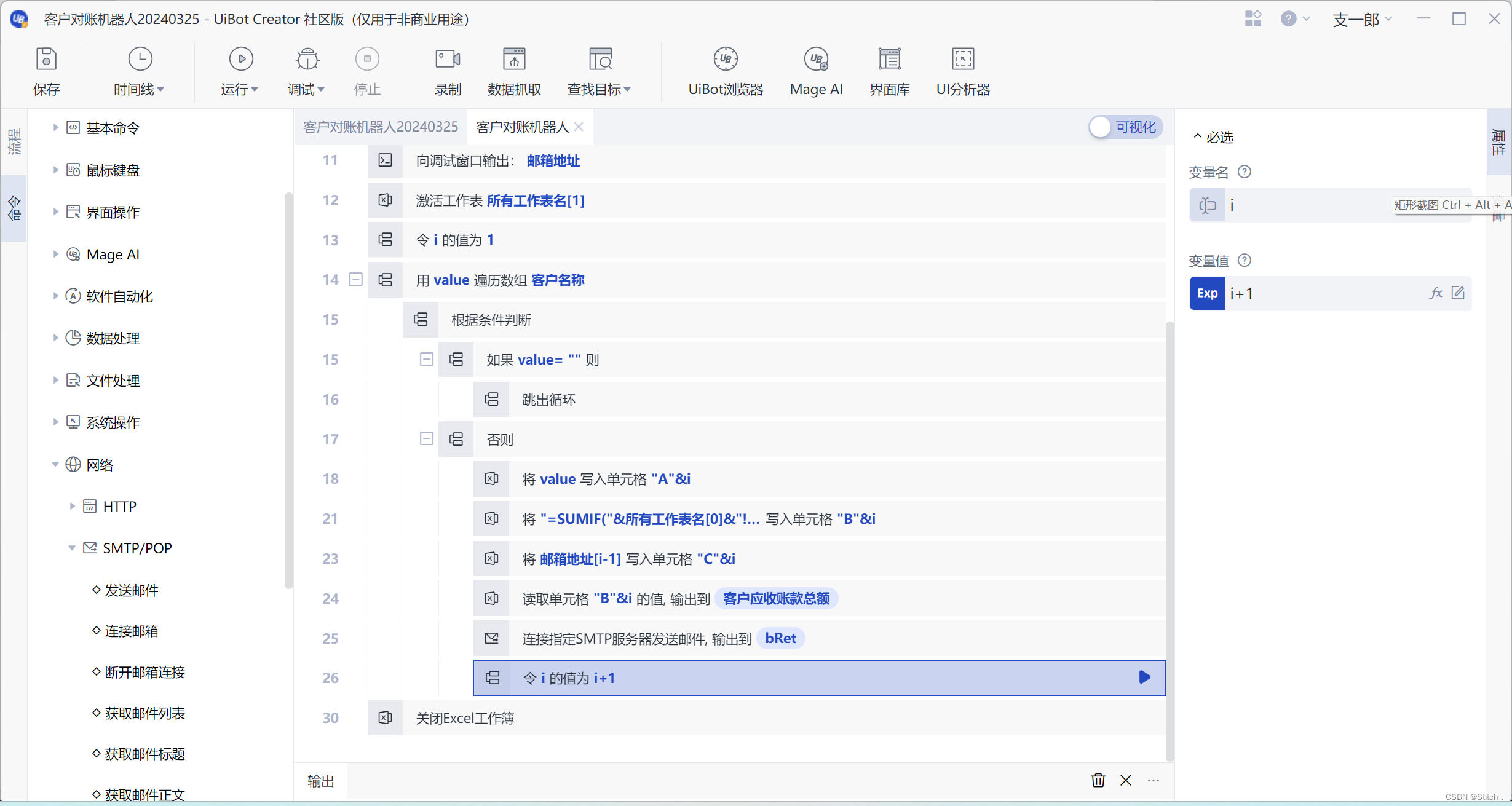
RPA-财务对账邮件应用自动化(客户对账机器人)
《财务对账邮件应用自动化》,将会使用邮箱的SMTP服务,小北把资源包绑定在这篇博客了 Uibot (RPA设计软件)———机器人的小项目友友们可以参考小北的课前材料五博客~ (本博客中会有部分课程ppt截屏,如有侵权请及请及时与小北我取得联系~) …...

Delphi模式编程
文章目录 Delphi模式编程涉及以下几个关键方面:**设计模式的应用****Delphi特性的利用****实际开发中的实践** Delphi模式编程的实例 Delphi模式编程是指在使用Delphi这一集成开发环境(IDE)和Object Pascal语言进行软件开发时,采用…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
