什么是L1和L2正则化,以及它们有什么区别
一、L1和L2正则化是什么?
在防止过拟合的方法中有L1正则化和L2正则化,L1和L2是正则化项,又叫做惩罚项,是为了限制模型的参数,防止模型过拟合而加在损失函数后面的一项。
在二维的情况下,黄色的部分是L2和L1正则项约束后的解空间,绿色的等高线是凸优化问题中目标函数的等高线,如下图所示。由图可知,L2正则项约束后的解空间是圆形,而L1正则项约束的解空间是多边形。显然,多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。
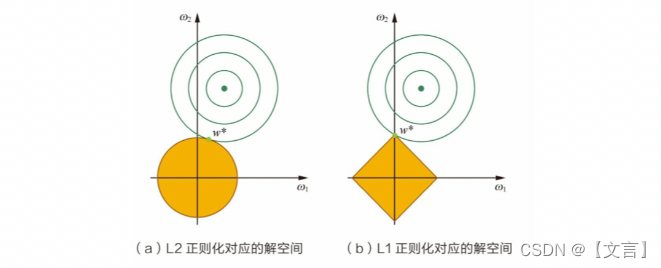
图片参考来源:《百面机器学习》
看完上面内容,进一步追求细节,为什么加入正则项就是定义了一个解空间约束? 为什么L1和L2的解空间是不同的?
这些问题其实可以通过KKT条件给出一种解释。
事实上,“带正则项”和“带约束条件”是等价的。为了约束w的可能取值空间从而防止过拟合,我们为该最优化问题加上一个约束,就是w的L2范数的平方不能大于m:
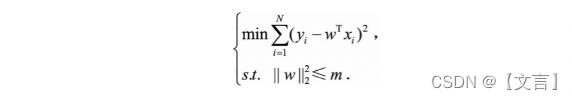
为了求解带约束条件的凸优化问题,写出拉格朗日函数
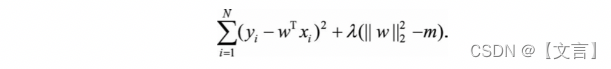
若w*和 λ*分别是原问题和对偶问题的最优解,则根据KKT条件,它们应满足
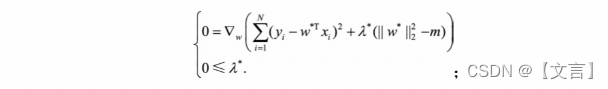
此时可以发现,上述第一个式子就是w*为带L2正则项的优化问题的最优解的条件,而λ*就是L2正则项前面的正则参数。
此时对问题的理解就更加深刻了。L2正则化相当于为参数定义了一个圆形的解空间(因为必须保证L2范数不能大于m),而L1正则化相当于为参数定义了个棱形的解空间。如果原问题目标函数的最优解不是恰好落在解空间内,那么约束条件下的最优解一定是在解空间的边界上,而L1“棱角分明”的解空间显然更容易与目标函数等高线在角点碰撞,从而产生稀疏解。
二、区别
区别一:
- L1是模型各个参数的绝对值之和。
- L2是模型各个参数的平方和的开方值。
区别二:
- L1会趋向于产生少量的特征,而其他的特征都是0。因为最优的参数值很大概率出现在坐标轴上,这样就会导致某一维的权重为0 ,产生稀疏权重矩阵;
- L2会选择更多的特征,这些特征都会接近于0。最优的参数值很小概率出现在坐标轴上,因此每一维的参数都不会是0。当最小化||w||时,就会使每一项趋近于0。
三、其他问题
-
为什么参数越小代表模型越简单?
- 越是复杂的模型,越是尝试对所有样本进行拟合,包括异常点。这就会造成在较小的区间中产生较大的波动,这个较大的波动也会反映在这个区间的导数比较大。只有越大的参数才可能产生较大的导数。因此参数越小,模型就越简单。
-
实现参数的稀疏有什么好处?
- 因为参数的稀疏,在一定程度上实现了特征的选择。一般而言,大部分特征对模型是没有贡献的。这些没有用的特征虽然可以减少训练集上的误差,但是对测试集的样本,反而会产生干扰。稀疏参数的引入,可以将那些无用的特征的权重置为0。
-
L1范数和L2范数为什么可以避免过拟合?
- 加入正则化项就是在原来目标函数的基础上加入了约束。当目标函数的等高线和L1,L2范数函数第一次相交时,得到最优解。
相关文章:
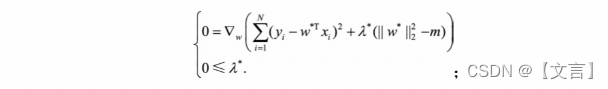
什么是L1和L2正则化,以及它们有什么区别
一、L1和L2正则化是什么? 在防止过拟合的方法中有L1正则化和L2正则化,L1和L2是正则化项,又叫做惩罚项,是为了限制模型的参数,防止模型过拟合而加在损失函数后面的一项。 在二维的情况下,黄色的部分是L2和…...
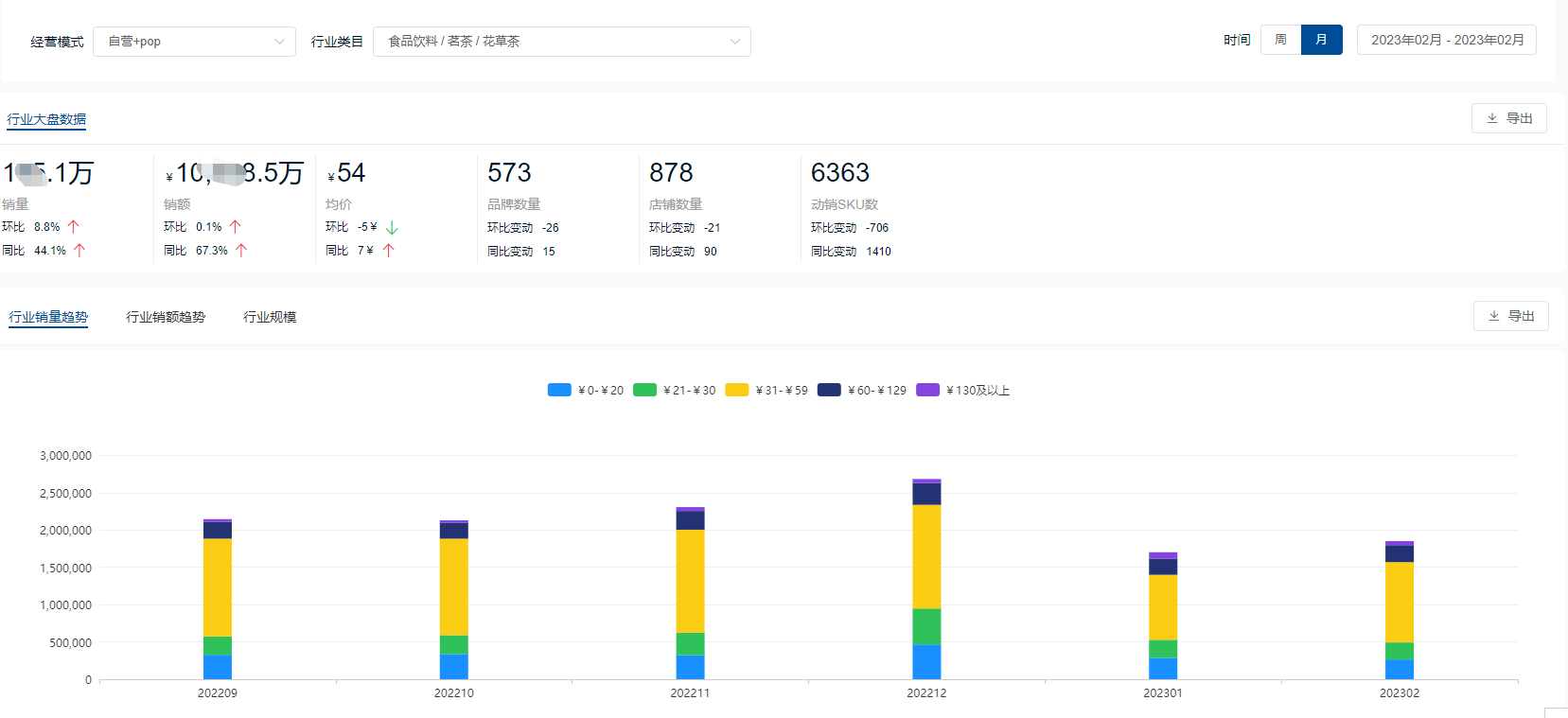
场景式消费激发春日经济,这些电商品类迎来消费热潮
春日越临近,商机越浓郁。随着气温渐升,春日经济已经潜伏在大众身边。“春菜”、“春装”、“春游”、“春季养生”等春日场景式消费走热。 下面,鲸参谋为大家盘点几个与春日经济紧密相关的行业。 •春日仪式之春游踏青 ——户外装备全面开花…...
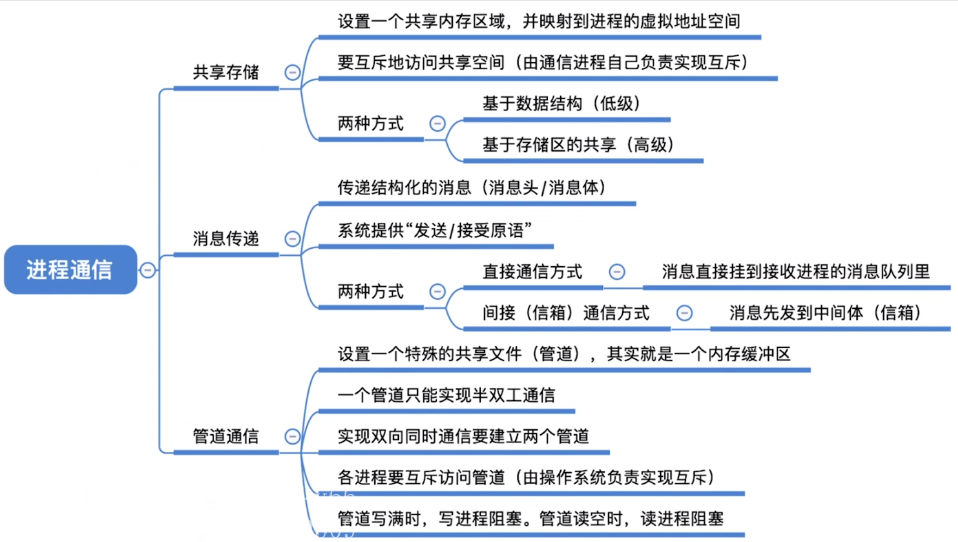
[2.1.4]进程管理——进程通信
文章目录第二章 进程管理进程通信(IPC)为什么进程通信需要操作系统支持?(一)共享存储(1)基于存储区的共享(2)基于数据结构的共享(二)消息传递什么…...

ChatGPT也有犯晕的时候
前面测试 ChatGPT 进行写代码、优化代码、解释代码、一般问答都表现的很好。偷个懒,用ChatGPT 帮我写段生物信息代码如果 ChatGPT 给出的的代码不太完善,如何请他一步步改好?代码看不懂?ChatGPT 帮你解释,详细到爆&…...

机器学习与目标检测作业:连通块算法
机器学习与目标检测作业:连通块算法一、连通块算法题目描述二、连通块算法文件结构三、连通块算法程序编写3.1、连通块算法conBlock.h头文件内容3.2、conBlock.cpp源文件内容3.3.3、mian.h头文件内容3.3.4、main.cpp源文件内容如下四、连通块算法程序运行结果一、连…...

HBase基础 --- 增删查改
目录 创建表 查看指定表全名空间中的表 查看表描述 禁用/启用 查看禁用/启动状态 删除表 新增列族 删除列族 更改列族存储版本的限制 增加数据 根据条件查询 查看指定列中不同版本的数据 删除指定列族下的指定列 删除指定行 全表扫描 全表扫描指定列族…...

如何基于AI智能视频技术实现公园景区的人流量实时统计?
一、方案背景春暖花开的季节来临,外出旅游的人群也越来越多。无论是景区、公园、博物馆、步行街等场所,客流超载非常大,给游客带来的体验较差,同时也存在安全隐患。当前景区面临的管理痛点包括:客流信息查询难…...

【JavaWeb】Servlet详解
文章目录1. 前置知识2.servlet生命周期2.1 默认情况下,服务器启动时,servlet对象并没有被创建2.2 用户执行一次请求2.3用户执行第二次请求2.4 3,4,5,6....次请求2.5 关闭服务器3.servlet方法解析4.适配器模式改造servlet4.1不使用servlet模式4.2使用适配…...
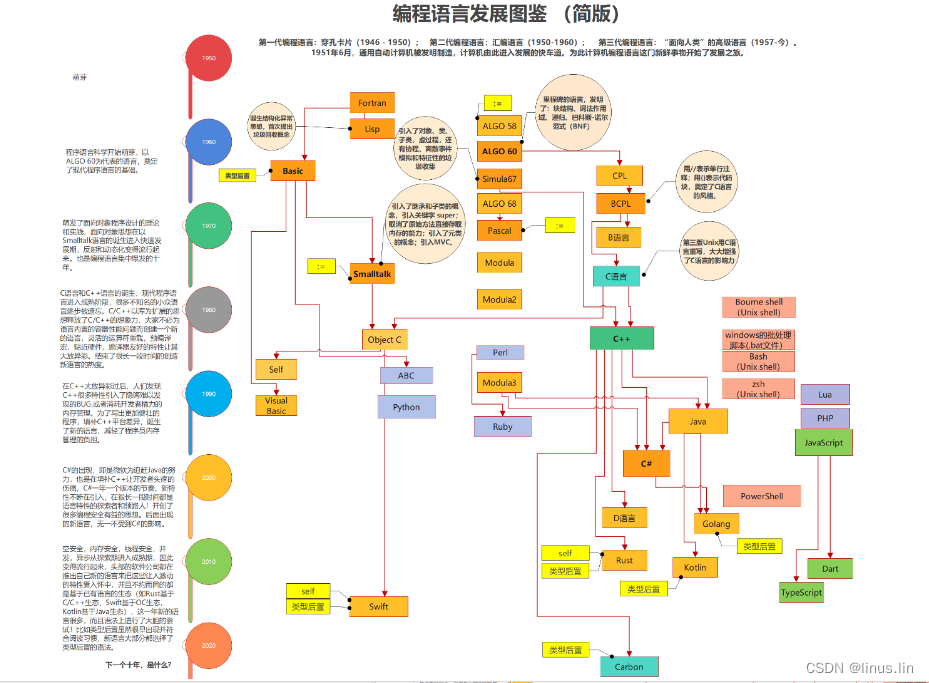
谁是世界上最好的编程语言?--编程语言70年浅谈
1、编程语言发展史纵览 严谨起见,本文提到的编程语言指的是「第三代高级编程语言」。 首先,我们从时间维度入手聊聊编程语言。一图胜千言,我们从目前主流的编程语言中,挑选出流行的、具有历史影响力的语言。把它们按时间从上往下…...
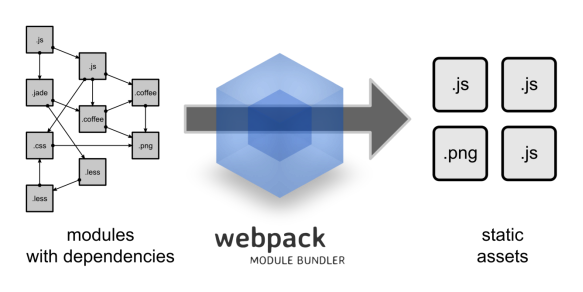
Webpack前端资源加载/打包工具
文章目录一、Webpack1、什么是Webpack2、Webpack安装2.1全局安装2.2安装后查看版本号3、创建项目3.1初始化项目3.2创建src文件夹3.3 src下创建common.js3.4 src下创建utils.js3.5 src下创建main.js4、JS打包4.1创建配置文件4.2执行编译命令4.3创建入口页面4.4测试5、CSS打包5.1…...

springcloud3 fegin实现服务调用1
一 Fegin的作用 1.1 fegin的作用 fegin是一个声明式的web服务客户端,让编写web服务器客户端变得非常容易,只需创建一个接口并在接口中添加FeginClients注解即可。 Fegin的使用方式:使用fegin的注解定义接口,调用这个接口&#…...

专业版即将支持自定义场景测试
物联网 MQTT 测试云服务 XMeter Cloud 专业版于 2022 年底上线后,已有不少用户试用,对数千甚至上万规模的 MQTT 并发连接和消息吞吐场景进行测试。同时我们也收到了希望支持更多物联网协议测试的需求反馈。 新年伊始,XMeter 团队全力聚焦于 …...
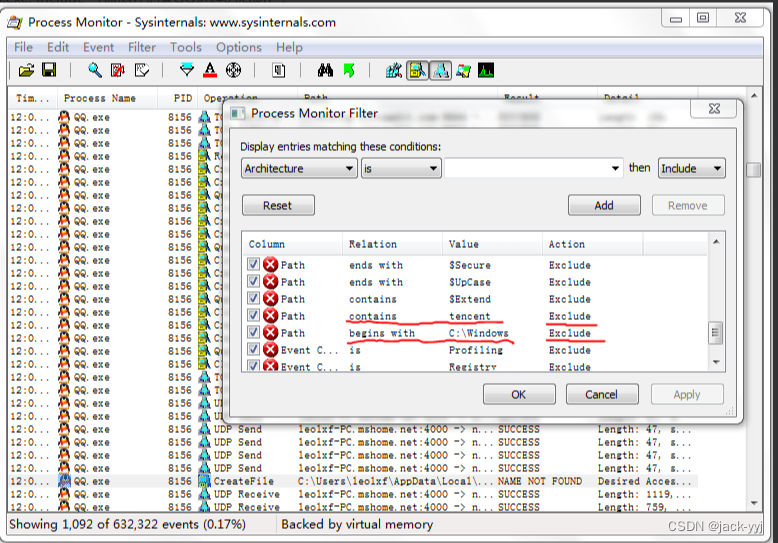
Process Monitor工具使用实验(23)
实验目的 学习Process Monitor实用小工具的使用,学会利用Process Monitor工具观察程序进程/线程、文件系统、注册表、网络连接等的活动。预备知识 Process Monitor是一个Windows系统下先进的监视工具,它可以显示文件系统、注册表、网络连接、进程…...
钓鱼客服到拿下服务器全过程(重点在于钓鱼添加img src)
重点总结 钓鱼时主动在变量中添加了字段,等待用户点击获取ip信息进行下一步资金盘plus呢 左看右看没啥东西,看看客服系统能不能打xss。 吊毛客服居然不在线,这套客服系统见过是whisper,之前审计过没有存储xss 但能通过伪造图片…...
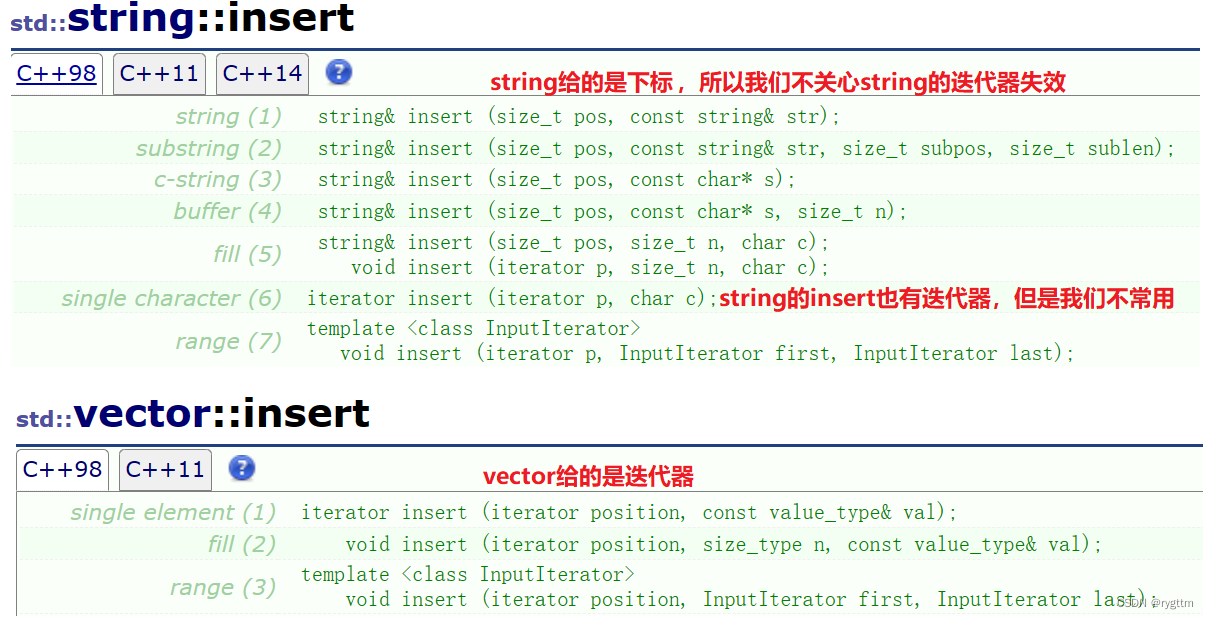
【C++】list迭代器的深度剖析及模拟实现(感受类封装,类和对象的思想)
早点睡兄弟,别一天到晚就熬夜。 文章目录一、通过list迭代器来感受类和对象以及类封装的思想1.迭代器的特征和本质是什么?(两大特征:类的内嵌类型,行为像指针。本质:内置类型定义的变量或自定义类型实例化…...

JavaScript 语句、注释和代码块实例集合
文章目录JavaScript 语句、注释和代码块实例集合JavaScript 语句JavaScript 代码块JavaScript 单行注释JavaScript 多行注释使用单行注释来防止执行使用多行注释来防止执行JavaScript 语句、注释和代码块实例集合 JavaScript 语句 源码 <!DOCTYPE html> <html> &…...
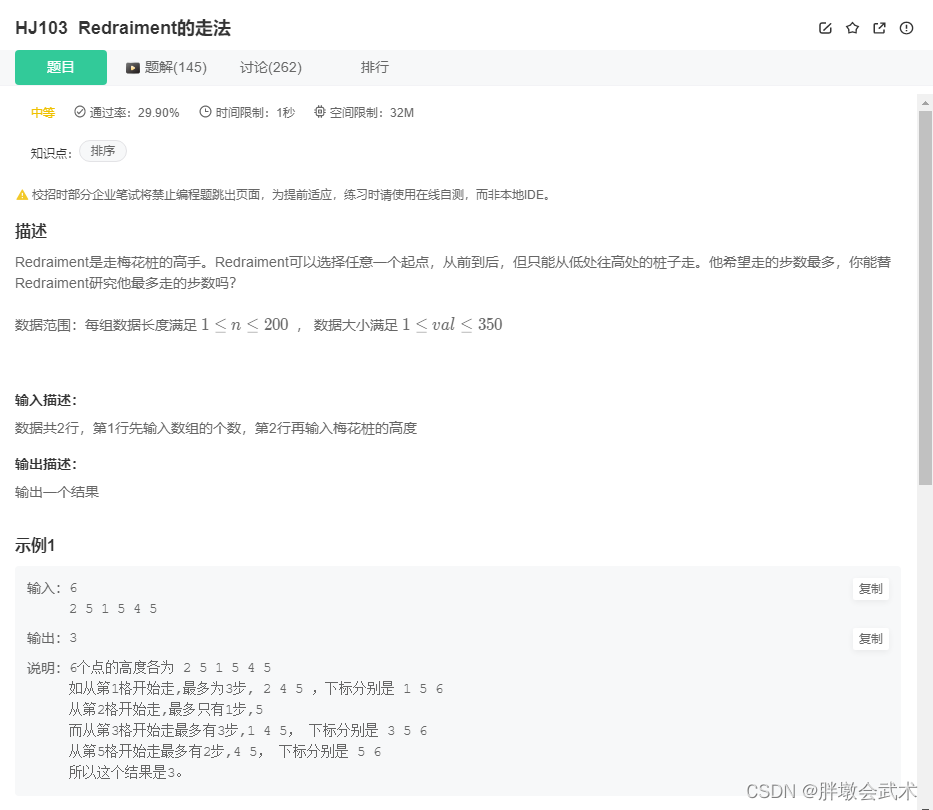
华为机试题:HJ103 Redraiment的走法(python)
文章目录(1)题目描述(2)Python3实现(3)知识点详解1、input():获取控制台(任意形式)的输入。输出均为字符串类型。1.1、input() 与 list(input()) 的区别、及其相互转换方…...

html+css 实现 熊猫样式
效果 html代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv"X-UA-Compatible"…...

Vue基础19之插槽
Vue基础19插槽不使用插槽App.vueCategory.vue默认插槽:slotApp.vueCategory.vue具名插槽App.vueCategory.vue作用域插槽App.vueCategory.vue总结插槽 不使用插槽 App.vue <template><div class"bg"><Category :listData"food"…...
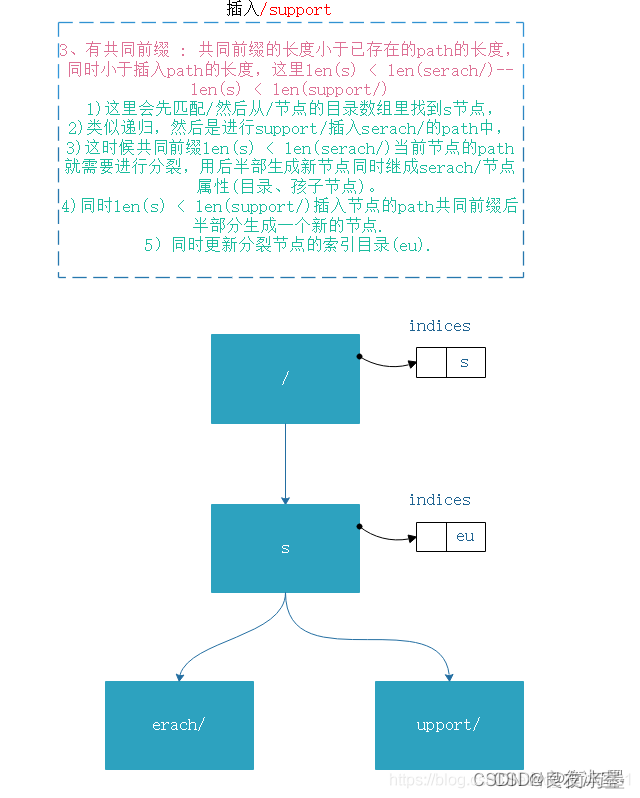
[Gin]框架底层实现理解(一)
前言:路由原理———压缩字典 这边简单讲一下gin非常重要的一个基点,也就是他作为go web框架的一个亮点 也就是Trie树和压缩字典算法 gin 通过树来存储路由,讲路由的字符拆解为一个个的结点,在获取handler函数时,会…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...

Django RBAC项目后端实战 - 03 DRF权限控制实现
项目背景 在上一篇文章中,我们完成了JWT认证系统的集成。本篇文章将实现基于Redis的RBAC权限控制系统,为系统提供细粒度的权限控制。 开发目标 实现基于Redis的权限缓存机制开发DRF权限控制类实现权限管理API配置权限白名单 前置配置 在开始开发权限…...

更新 Docker 容器中的某一个文件
🔄 如何更新 Docker 容器中的某一个文件 以下是几种在 Docker 中更新单个文件的常用方法,适用于不同场景。 ✅ 方法一:使用 docker cp 拷贝文件到容器中(最简单) 🧰 命令格式: docker cp <…...

机器学习复习3--模型评估
误差与过拟合 我们将学习器对样本的实际预测结果与样本的真实值之间的差异称为:误差(error)。 误差定义: ①在训练集上的误差称为训练误差(training error)或经验误差(empirical error&#x…...
