保研线性代数机器学习基础复习1
1.什么是代数(algebra)?
为了形式化一个概念,构建出有关这个概念的符号以及操作符号的公式。
2.什么是线性代数(linear algebra)?
一项关于向量以及操作向量的公式的研究。
3.举一些向量的例子?
- 几何向量(Gemometric vectors):可以进行add操作也可以multiply by标量,帮助我们在方向direction和大小magnitude方面去推理数学操作。
- 多项式(Polynomial):y=x2+x3+x4...
- 音频信号(Audio signals):音频信号是一系列数字,我们可以把音频信号加和(add),亦可以以一定λ大小扩大(multiply)。
:n元组是指n维向量,也是为了方便编程语言中array的表示。
4.什么是线性方程组(system of linear equation)?
其中,是这个式子的未知量,每一个满足这个方程组的n元组都可以称为线性方程组的一个解。
5.实数线性方程组的解(solution)有哪些情况?
要么无解,要么有一个解,要么有多个解。
如果是,那么可以看做二维平面两条直线相交,那么结果是1.无交集2.一个点3.一条直线。如果是
,那么可以看做是在三维立体空间两个平面相交,结果可能是1.一个平面2.一条直线3.一个点4.空。
6.什么是点积(dot product),也称作Hadamard product?
对于元素,我们用矩阵A的第i行与矩阵B的第j列逐个元素相乘,然后相加。
7.什么是单位矩阵(Identity Matrix)?
在n阶方阵中,只是在对角(diagonal)元素值为1,在其他元素值为0。
8.矩阵有哪些性质(property)?
- 结合性:

- 分配性:
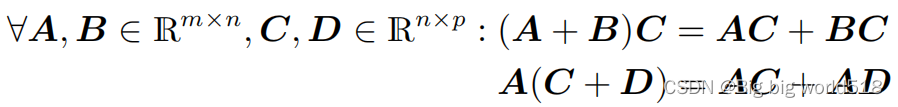
- 和单位矩阵相乘:

9.什么是矩阵的逆(inverse)?
对于n行n列的矩阵A和n行n列的矩阵B,如果满足,B被叫做A的逆。如果B存在,那么称A为正则矩阵/可逆矩阵/非奇异矩阵(regular/invertible/nonsingular)。如果矩阵的行列式(determinant)不为零,那么可以认为矩阵可逆。
10.什么是矩阵的转置(transpose)?
对于m行n列的矩阵A,A的转置B是n行m列,A的每一行作为B的每一列。如果A可逆,那么B(A的转置)爷可逆。
11.关于矩阵的逆和矩阵的转置的性质?
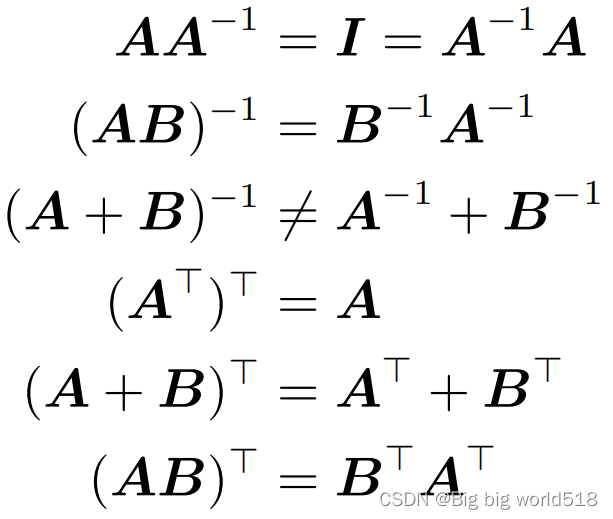
12.求解线性方程组的过程?
- 寻找
的特解
- 寻找
的所有解
- 将步骤一和步骤二的所有解结合起来得到通解(general solution)
13.什么是高斯消元法(Gaussian elimination)
高斯消元法是通过初等变换(elementary transformation)把一个线性方程组的增广矩阵(augmented matrix),譬如,那么其增广矩阵为
,变成一个行递减的形式(reduced row-echelon)。
14.行递减阶梯矩阵有什么特点?
- 是一个行阶梯的形式
- 每个枢轴的值都是1
- 每一列只有唯一一个枢轴是这一列不为零的值
15.什么是广义逆矩阵(Moore-Penrose pseudo-inverse)?
通常情况我们定义逆矩阵针对的是方阵,但是如果一个非方阵矩阵,它的各个列向量是线性无关(linear independent),那么我们我们可以使用如下方法求解:
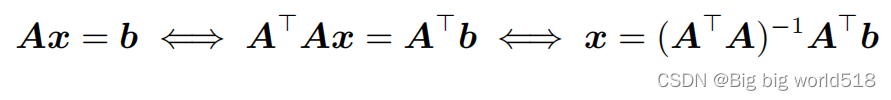
其中解被称为广义逆矩阵。
相关文章:
保研线性代数机器学习基础复习1
1.什么是代数(algebra)? 为了形式化一个概念,构建出有关这个概念的符号以及操作符号的公式。 2.什么是线性代数(linear algebra)? 一项关于向量以及操作向量的公式的研究。 3.举一些向量的例子&#x…...

js绑定事件的方法
在JavaScript中,绑定事件的方法主要有以下几种: HTML属性方式:直接在HTML元素中使用事件属性来绑定事件。 html<button onclick"alert(Hello World!)">Click Me</button> DOM属性方式:通过JavaScript代码…...

是德科技keysight N9000B 信号分析仪
181/2461/8938产品概述: 工程的内涵就是将各种创意有机地联系起来,并解决遇到的问题。 CXA 信号分析仪具有出色的实际性能,它是一款出类拔萃、经济高效的基本信号表征工具。 它的功能十分强大,为一般用途和教育行业的用户执行测试…...

软考 - 系统架构设计师 - 架构风格
软件架构风格是指描述特定软件系统组织方式的惯用模式。组织方式描述了系统的组成构件,以及这些构件的组织方式,惯用模式指众多系统所共有的结构和语义。 目录 架构风格 数据流风格 批处理架构风格 管道 - 过滤器架构风格 调用 / 返回风格 主程序…...
CleanMyMac X2024专业免费的国产Mac笔记本清理软件
非常高兴有机会向大家介绍CleanMyMac X 2024这款专业的Mac清理软件。它以其强大的清理能力、系统优化效果、出色的用户体验以及高度的安全性,在Mac清理软件市场中独树一帜。 CleanMyMac X2024全新版下载如下: https://wm.makeding.com/iclk/?zoneid49983 一、主要…...

ES6 模块化操作
ES6模块化主要有两个操作:import 和 export 如果在html文件的script中引用模块的话,要设置<script type"module"> 一种导入导出方法: a.js//分别暴露 export let num 1 export function compute(a, b){return a b }//统…...

统计XML文件内标签的种类和其数量及将xml格式转换为yolov5所需的txt格式
1、统计XML文件内标签的种类和其数量 对于自己标注的数据集,需在标注完成后需要对标注好的XML文件校验,下面是代码,只需将SrcDir换成需要统计的xml的文件夹即可。 import os from tqdm import tqdm import xml.dom.minidomdef ReadXml(File…...

《操作系统导论》第14章读书笔记:插叙:内存操作API
《操作系统导论》第14章读书笔记:插叙:内存操作API —— 杭州 2024-03-30 夜 文章目录 《操作系统导论》第14章读书笔记:插叙:内存操作API1.内存类型1.1.栈内存:它的申请和释放操作是编译器来隐式管理的,所…...
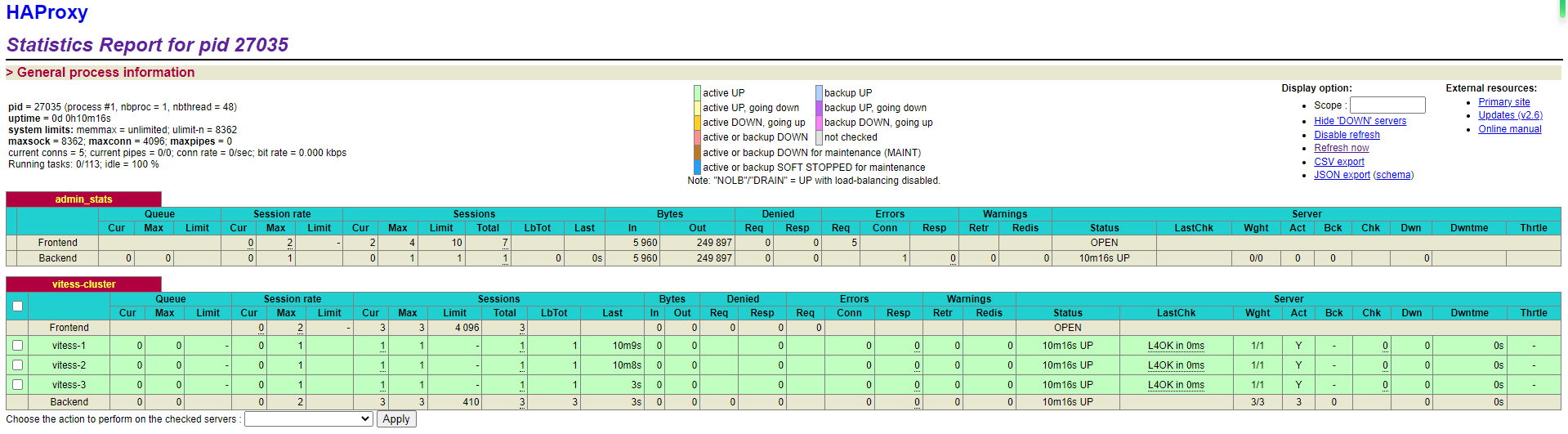
HAProxy + Vitess负载均衡
一、环境搭建 Vitess环境搭建: 具体vitess安装不再赘述,主要是需要启动3个vtgate(官方推荐vtgate和vtablet数量一致) 操作: 在vitess/examples/common/scripts目录中,修改vtgate-up.sh文件,…...

2024年京东云主机租用价格_京东云服务器优惠价格表
2024年京东云服务器优惠价格表,轻量云主机优惠价格5.8元1个月、轻量云主机2C2G3M价格50元一年、196元三年,2C4G5M轻量云主机165元一年,4核8G5M云主机880元一年,游戏联机服务器4C16G配置26元1个月、4C32G价格65元1个月、8核32G费用…...

qt-C++笔记之QSpinBox控件
qt-C笔记之QSpinBox控件 code review! 文章目录 qt-C笔记之QSpinBox控件1.运行2.main.cpp3.main.pro4.《Qt6 C开发指南》:4.4 QSpinBox 和QDoubleSpinBox 1.运行 2.main.cpp #include <QApplication> #include <QSpinBox> #include <QPushButton&g…...

Linux(CentOS)/Windows-C++ 云备份项目(服务器网络通信模块,业务处理模块设计,断点续传设计)
此模块将网络通信模块和业务处理模块进行了合并 网络通信通过httplib库搭建完成业务处理: 文件上传请求:备份客户端上传的文件,响应上传成功客户端列表请求:客户端请求备份文件的请求页面,服务器响应文件下载请求&…...
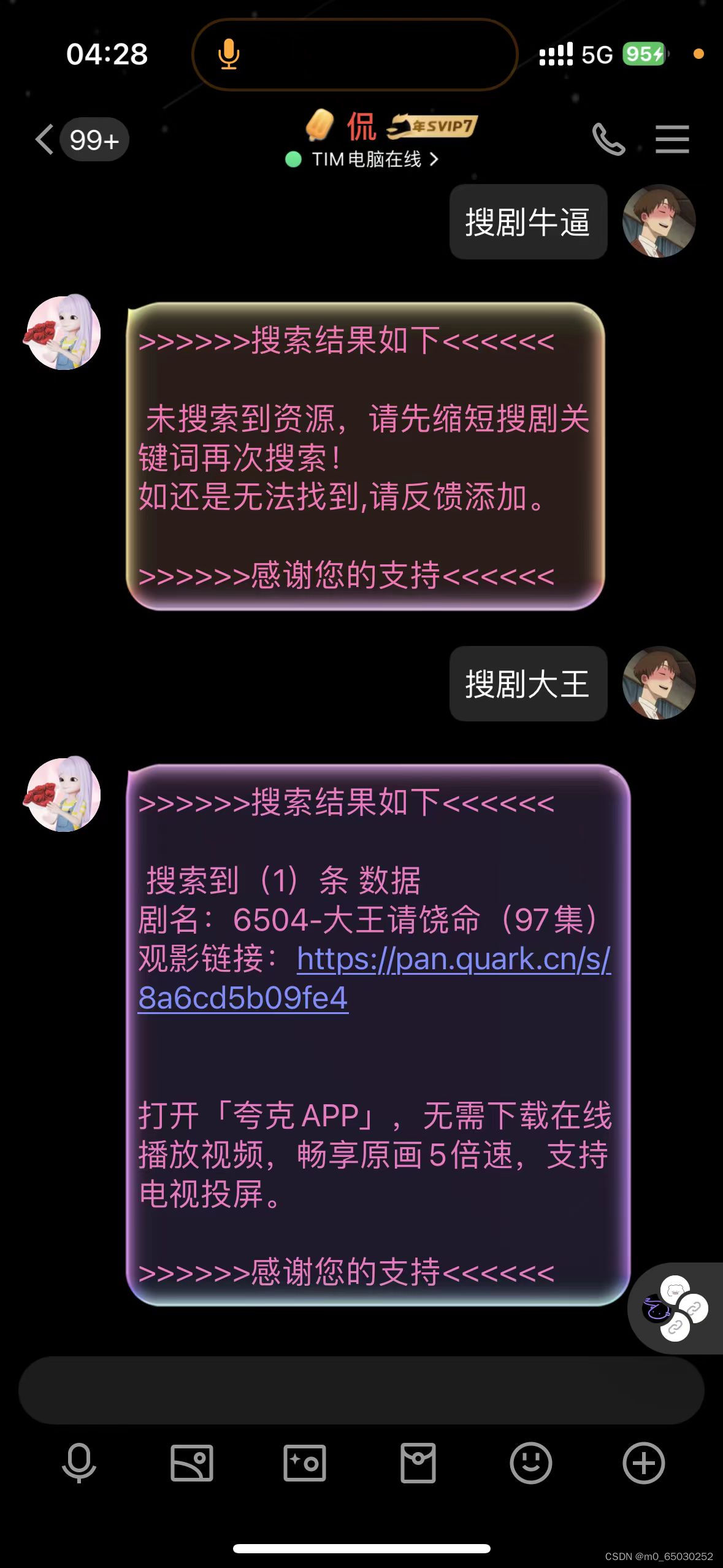
【QQ版】QQ群短剧机器人源码 全网短剧机器人插件
内容目录 一、详细介绍二、效果展示2.效果图展示 三、学习资料下载 一、详细介绍 QQ版本可以兼容两个框架(HTQQ,MYQQ这两个的vip版也可以使用) 支持私聊与群聊,命令是 搜剧影视关键词 如果无法搜索到影视资源,请使用下方命令&…...

矩阵间关系的建立
参考文献 2-D Compressive Sensing-Based Visually Secure Multilevel Image Encryption Scheme 加密整体流程如下: 我们关注左上角这一部分: 如何在两个图像之间构建关系,当然是借助第3个矩阵。 A. Establish Relationships Between Different Images 简单说明如下: …...

【C++】C到C++的入门知识
目录 1、C关键字 2、命名空间 2.1 命名空间的定义 2.2 命名空间的使用 2.2.1 加命名空间名称及作用域限定符 2.2.2 使用using将命名空间中某个成员引入 2.2.3 使用using namespace 命名空间名称引入 3、C输入&输出 4、缺省参数 4.1 缺省参数的概念 4.2 缺省参数的…...

【c++】简单的日期计算器
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好啊,在我们学习了默认成员函数后,我们本节内容来完成知识的实践,来实现一个简易的日期计算器 目录 头文件声明函数函数的实现1.全缺省默认构…...

基于easyx库的C/C++游戏编程实例-飞机大战
飞机大战游戏设计 首先创建飞机/子弹结构: struct Plane {int x;int y;bool live;int width;int height;int type;int hp; }player,bul[BUL_NUM],enemy[ENE_NUM];你需要加载图片: void ImageLoad() {//背景loadimage(&bg[0], "./image/飞机大…...

stitcher类实现多图自动拼接
效果展示 第一组: 第二组: 第三组: 第四组: 运行代码 import os import sys import cv2 import numpy as npdef Stitch(imgs,savePath): stitcher cv2.Stitcher.create(cv2.Stitcher_PANORAMA)(result, pano) stitcher.st…...

Ubuntu下udp通信
一、知识准备阶段 socket是什么?套接字是什么? https://blog.csdn.net/m0_37925202/article/details/80286946 Socket程序从Windows移植到Linux下的一些注意事项 sockaddr和sockaddr_in详解 bzero和memset函数 函数原型:void bzero&…...

拌合楼管理软件开发(十三) 对接耀华XK3190-A9地磅(实战篇)
前言: 实战开整 目前而言对于整个拌合楼管理软件开发,因为公司对这个项目还处于讨论中,包括个人对其中的商业逻辑也存在一些质疑,都是在做一些技术上的储备.很早就写好了串口与地磅对接获取代码,也大概知道真个逻辑,这次刚好跟库区沟通,远程连接到磅房电脑,开始实操一下. 一、地…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
