查找算法及查找常用数据结构总结
1.顺序表查找
基本方法:
设查找表以一维数组来存储,要求在此表中查找出关键字的值为x的元素的位置,若查找成功,则返回其位置(即下标),否则,返回一个表示元素不存在的下标(如0或-1)。
1.1简单顺序查找
基本思想: 遍历整个顺序表逐个比较,如果关键字相等则返回其下标,如果没有找到则返回-1。
//从左向右查找
int search (elementtype A[],keytype x) { int i;for(i = 0; i < n; i++) if (A[i].key==x)return(i);return(-1);
}//从右向左查找
int search ( elementtype A[],keytype x) {int i;for(i = n-1; i >= 0; i--) if (A[i].key == x) return(i);return(i);
}//监视哨,这里数据存放在下标1~n
int search ( elementtype A[],keytype x) {int i = n;A[0].key=x;while (A[i].key != x) i--;return(i);
}
1.2 二分查找
基本思想: 设查找区域的首尾下标分别用变量low和high表示(初值分别为0和n-1,其中数组的下标从0开始,这与简单顺序查找中略有不同),将待查关键字x和该区域的中间元素 (其下标mid的值为low和high的算术平均值,即(low+high)/2) 的关键字进行比较,并根据比较的结果分别作如下处理:
- x==A[mid].key:查找成功,返回mid的值。
- x<A[mid].key:说明待查元素只可能在左边区域(下标从low到mid-1),因此,应在此区域继续查找。
- x>A[mid].key:说明待查元素只可能在右边区域(下标从mid+1到high) ,因此,应在此区域继续查找。
若表中存在所要查找的元素,则经过反复执行上述过程可以很快地找到,并返回元素下标,否则,返回-1以表示查找失败。
//首先要把握下面几个要点:
//right=n-1 => while(left <= right) => right=middle-1;
//right=n => while(left < right) => right=middle;
//middle的计算不能写在while循环外,否则无法得到更新。 /*!
* @brief 非递归二分查找
*
* @param[in] elements:存放有序元素的数组
* @param[in] key:待查找的元素
* @param[in] size:数组的尺寸
* @return 数组中key的下标,没有则返回-1
*/
template<typename T>
int binSearch(T* elements, T key, int size) {int low = 0, high = size - 1;while (low <= high) {//计算时避免值溢出int mid = low + ((high - low) >> 1);if (elements[mid] > key) {high = mid - 1;}else if (elements[mid] < key) {low = mid + 1;}else {return mid;}}return -1;}/*!
* @brief 递归二分查找
*
* @param[in] elements:存放有序元素的数组
* @param[in] key:待查找的元素
* @param[in] low:下界
* @param[in] high:上界
* @return 数组中key的下标,没有则返回-1
*/
template<typename T>
int binSearch(T* elements, T key, int low, int high) {//递归终止条件if (low > high) {return -1;}else {//计算时避免值溢出int mid = low + ((high - low) >> 1);if (elements[mid] > key) {return binSearch(elements, key, low, mid - 1);}else if (elements[mid] < key) {return binSearch(elements, key, mid + 1, high);}else {return mid;}}
}
1.3 索引表查找
核心思想是块间有序,块内无序;首先在索引表间查找确定元素所在的块,然后在确定的块中查找;
- 块间查找:在索引表中查找既可以用简单顺序查找,也可以用二分查找;
- 块内查找:在块内查找只能用顺序查找;
1.4 算法分析
| 查找方法 | 平均查找长度 | 最坏查找长度 |
|---|---|---|
| 简单顺序查找 | (n+1)/2 | n |
| 二分查找 | l o g 2 ( n + 1 ) − 1 log_2(n+1)-1 log2(n+1)−1 | l o g 2 ( n ) + 1 log_2(n)+1 log2(n)+1 |
注:二分查找平均查找长度计算过程
2.树表查找
2.1 二叉排序树(BST树)
定义: 二叉排序树是一棵二叉树,或者为空,或者满足以下条件:
- 若左子树不空,则左子树中所有结点的值小于根结点的值;
- 若右子树不空,则右子树中所有结点的值不小于根结点的值;
- 左右子树都为二叉排序树。
/*** 非递归二叉排序树查找* * @tparam T* @param tree* @param x* @return*/
template<typename T>
Node<T> *bstsearch(Node<T> *tree, T x) {Node<T> *p = tree;while (p != nullptr) {if (p->data == x) {return p;}if (x < p->data) {p = p->lchild;} else {p = p->rchild;}}return nullptr;
}/*** 递归二叉排序树查找* * @tparam T * @param tree * @param x * @return */
template<typename T>
Node<T> *bstsearch(Node<T> *tree, T x) {if (tree == nullptr) {return tree;}if (tree->data == x) {return tree;}if (x < tree->data) {return bstsearch(tree->lchild, x);} else {return bstsearch(tree->rchild, x);}
}
二叉排序树的构造
核心:从空树出发,依次插入若干个节点;
步骤:
- 若该值小于根结点的值,则应往左子树中插入 (递归调用插入算法)。
- 若该值大于等于根结点的值,则往右子树中插入(递归调用)。
- 按此方式递归调用若干次后,总可以搜索到一个空子树位置,即要插入的位置。
/*** 在树tree中插入节点curNode* * @tparam T * @param tree * @param curNode */
template<typename T>
void insert(Node<T> *&tree, Node<T> *curNode) {if (tree == nullptr) {tree = curNode;return;}if (curNode->data < tree->data) {insert(tree->lchild, curNode);} else {insert(tree->rchild, curNode);}
}/*** 基于控制台输入,创建二叉排序树* * @tparam T * @param tree */
template<typename T>
void create(Node<T> *&tree) {tree = nullptr;int x;cin >> x;while (x != 0) {Node<int>* node = new Node(x);insert(tree, node);cin >> x;}
}
该构造方式的问题是,当输入是一个递增或者递减序列时,则该树是相当倾斜的,即左右子树的深度差距很大;
二叉排序树删除结点
删除只能和删除结点,不能删除以结点为根的子树,且还要保证删除后所得二叉树仍满足二叉排序树的性质不变。
1.被删除的结点是叶子结点:直接删去该结点。
2.被删除的结点只有右子树或者只有左子树,用其右子树或者左子树替换
3.被删除的结点既有左子树又有右子树,找到删除结点的左子树中的最大值,将其替换删除结点(或者找右子树上最小的结点)
2.2 平衡二叉树(AVL树)
定义:
平衡二叉树是一棵二叉排序树,或者为空,或者满足以下条件:
- 左右子树高度差的绝对值不大于1;
- 左右子树都是平衡二叉树。
平衡因子:
左子树的高度减去右子树的高度,其值为-1,0或1。
对于一颗有n个结点的AVL树,其高度保持在O(log2n)数量级,平均查找长度(ASL)也保持在O(log2n)量级。
如何构造平衡二叉树
在平衡的二叉排序树中插入一个结点,当出现不平衡时,根据不平衡情况分四种调整方法
——假设最低不平衡结点为A,根据新插入结点与A的位置关系来命名调整方法:
LL型:新插入结点在A的左孩子(L)的左子树(L)中;

LR型:新插入结点在A的左孩子(L)的右子树®中;

RL型:新插入结点在A的右孩子®的左子树(L)中;
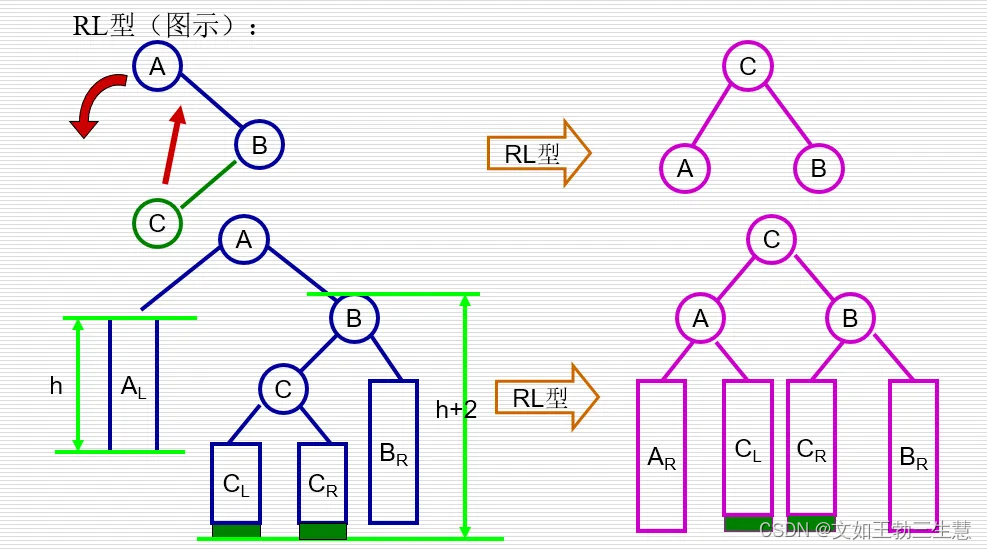
RR型:新插入结点在A的右孩子®的右子树®中。
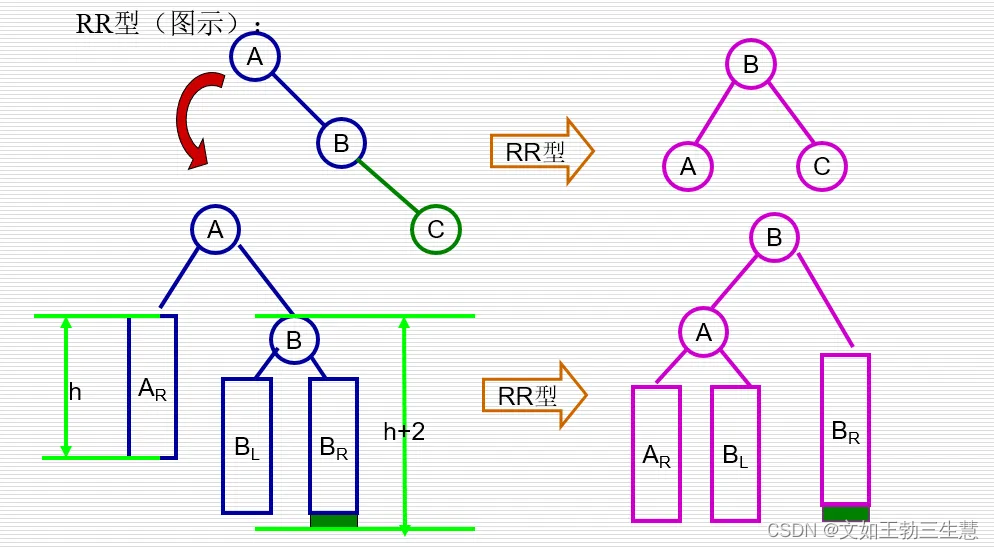
2.3 红黑树(RBT)
红黑树(Red-Black Tree)也是是一种自平衡的二叉搜索树,与AVL树不同的是它在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出两倍(最长路径也不会超出最短路径的两倍,因此红黑树的平衡性要求相对宽松,没有AVL树那样严格),从而使搜索树达到一种相对平衡的状态。
红黑树具有以下性质:
- 每个结点不是黑色就是红色;
- 根结点必须是黑色的
- 红色结点的两个子结点必须都是黑色的,这保证了没有两个连续的红色节点相连
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点,也被称为NIL节点或者NULL节点)
- 任意结点到其每个叶子结点的简单路径上,黑色节点的数量相同:确保了树的黑平衡性,即红黑树中每条路径上黑色结点的数量一致。
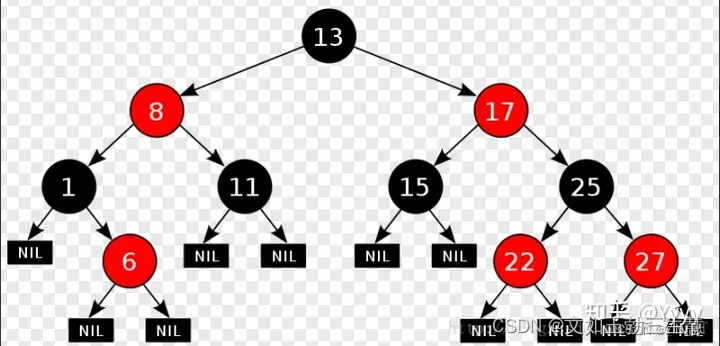
所以我们这里来分析一种极端的情况:
大家想,如果一棵红黑树有红有黑,它里面如果有一条全黑的路径,那这条全黑的路径一定就是最短路径; 如果有一条是一黑一红,一黑一红…,这样黑红相间的,那他就是最长的路径。 然后它们里面的黑色结点个数又是相同的的,所以最长路径最多是最短路径的两倍,不可能超过最短路径两倍。 所以这样红黑树的高度就能够保持在一个相对平衡的范围内,当然他就没有AVL树那么严格
红黑树的插入
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
- 按照二叉搜索的树规则插入新节点,除了根节点为黑色,新插入的节点初始为红色;
- 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整。但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树进行调整;
调整的总体思路是重新着色或者旋转+重新着色,旋转的思路跟AVL树类似,详见 https://zhuanlan.zhihu.com/p/659174741
红黑树的删除
将红黑树内的某一个节点删除,需要执行哪些步骤呢? ⑴首先,红黑树是一棵二叉查找树,按照二叉查找树的节点删除规则删除该节点;⑵然后,通过旋转和重新着色操作来修正该树的红黑树特性。详细步骤如下:
第一步:将节点按照二叉查找树的删除规则进行节点删除。
这和“删除常规二叉查找树中的节点方法是一样的”。分3种情况:
Ⅰ.被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。
Ⅱ.被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。
Ⅲ.被删除节点有两个儿子。那么,先找出它的[前驱节点/后继节点];然后把“它的[前驱节点/后继节点]的内容”复制给“该节点”;之后,删除“它的[前驱节点/后继节点]”。在这里,[前驱节点/后继节点]相当于替身,在将[前驱节点/后继节点]的内容复制给"被删除节点"之后,再将[前驱节点/后继节点]删除。这样就巧妙的将问题转换为“删除[前驱节点/后继节点]”的情况了,下面就考虑[前驱节点/后继节点]。在"被删除节点"有两个非空子节点的情况下,它的[前驱节点/后继节点]不可能是双子非空。既然"[前驱节点/后继节点]"不可能双子都非空,就意味着"该节点的[前驱节点/后继节点]"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况Ⅰ"进行处理;若只有一个儿子,则按"情况Ⅱ"进行处理。
查找效率分析
对于一棵红黑树来说,如果它里面全部的黑色结点一共有N个的话,那它的最短路径长度就差不多是 l o g 2 ( N ) log_2 (N) log2(N)。 然后整棵树的节点数量就是在【N,2N】之间。 所以最长路径长度就可以认为差不多是 2 l o g 2 ( N ) 2log_2 (N) 2log2(N) 所以红黑树的查找最少是 l o g 2 ( N ) log_2 (N) log2(N)次,最多是 2 l o g 2 ( N ) 2log_2 (N) 2log2(N)次,所以红黑树查找的时间复杂度是O( l o g 2 N log_2 N log2N),计算时间复杂度前面的常数项可以省略。 而AVL树也是O( l o g 2 N log_2 N log2N),但AVL树是比较严格的O( l o g 2 N log_2 N log2N),而红黑树是省略了常数项。 所以严格来说,红黑树的查找效率是比不上AVL树的(但对于计算机来说是没什么差别的),但是它们是同一个数量级的,都是O( l o g 2 N log_2 N log2N)。
红黑树对比AVL树
由于AVL树要求更加严格的平衡,所以在进行插入和删除操作时,可能需要更频繁地进行旋转操作来调整树的结构,以保持平衡。相比之下,红黑树的插入和删除操作需要旋转的次数相对较少,因此在插入和删除操作频繁的情况下,红黑树可能更加高效。
综合来看,红黑树其实更胜一筹,红黑树在实际应用中更为常用,Java集合中的TreeSet和TreeMap,C++ STL中的set、map,以及Linux虚拟内存的管理,都是通过红黑树实现的;
第二步:通过旋转和重新着色操作来修正该树的红黑树特性。
因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
2.4 B树
注:B树有时候也会写作B-树,是一个意思;
定义:m阶B树(m≥3)满足如下条件:
- 每一个结点分支数≤m;
- 根结点分支数≥2(要求此根结点不为叶子结点);
- 其余分支结点的分支数≥ m/2 ;
- 所有叶子结点在同一层;
- 每一个结点的结构如下:
满足 A 0 < K 1 < A 1 < . . . < K m < A m A_0<K_1<A_1<...<K_m<A_m A0<K1<A1<...<Km<Am,其中Ai表示其中的所有关键字;
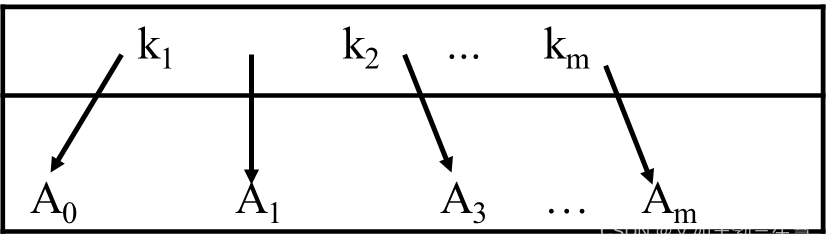
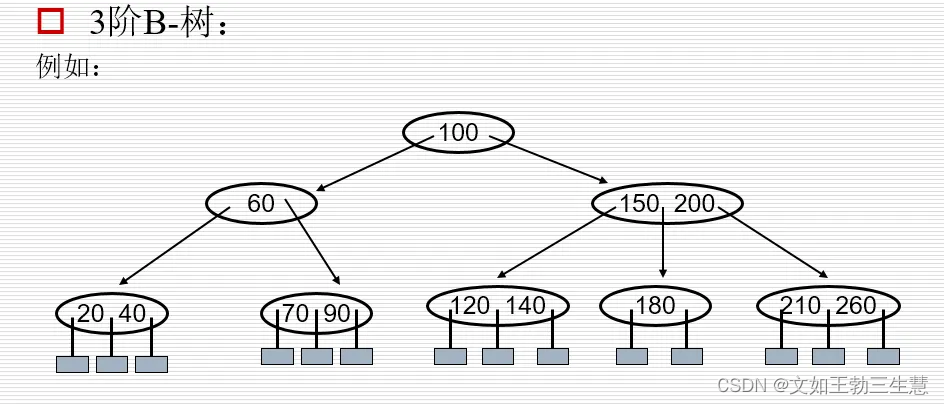
插入关键字——插入到叶子结点中
- 插入后,该结点的关键字个数 n<m, 不修改分支指针;
- 插入后,该结点的关键字个数 n=m, 则需进行“结点分裂”,令 s = m / 2 m/2 m/2, 在原结点中保留 (A0,K1,…… , Ks-1,As-1); 建新结点 (As,Ks+1,…… ,Kn,An); 将(Ks,p)插入双亲结点,p是指向新节点的指针;
3)若双亲为空,则建新的根结点。



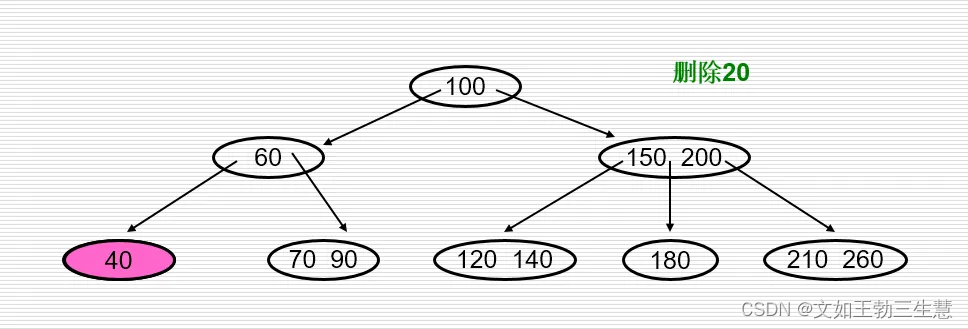
删除关键字
- 在深度为(h+l)的m阶B-树中删除一个键值k,首先要查到键值k所在的结点及在结点中的位置。若k在非叶子节点中,则把该结点的右边(或左边)指针所指子树中的最小(或最大)键值与k对调,使k移到有叶子节点。
- 在叶子节点中删除一个键值后,使得该结点的值个数n减1,此时应分以下三种情况进行处理: a.
- 若删除后结点中键值数目 n ≥ m / 2 − 1 n≥m/2-1 n≥m/2−1,在该结点中删去键值k连同右边的指针。 b.
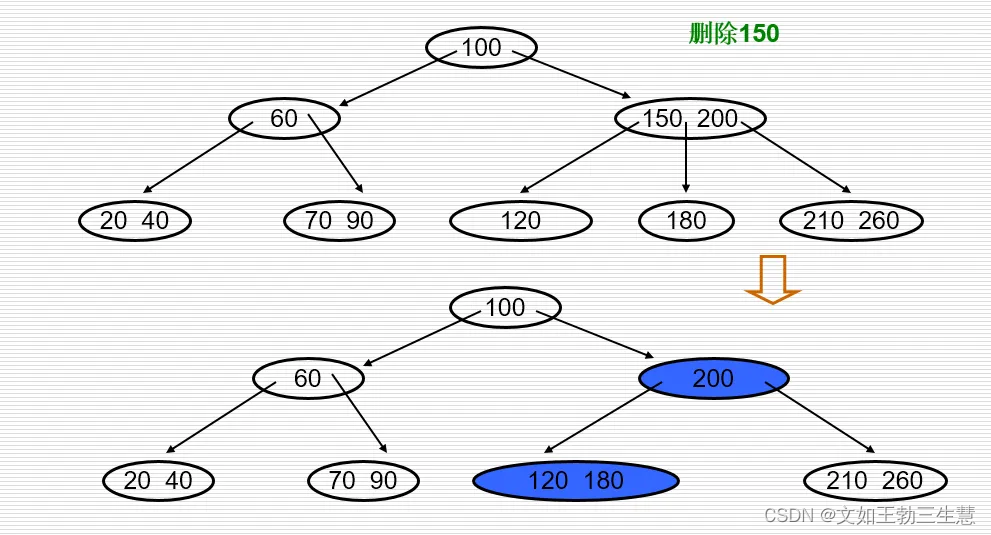
- 若删除后结点中键值数目 n < m / 2 − 1 n<m/2-1 n<m/2−1,且左(或右)兄弟结点的关键字数目> m / 2 − 1 m/2-1 m/2−1,则把左(或右)兄弟结点中最大(或最小)键值移到父结点中,再把父结点大于(或小于)上移键值的键值下移到被删关键字所在结点中。 c.
- 若删除后结点中键值数目 n < m / 2 − 1 n<m/2-1 n<m/2−1,及其左、右兄弟结点的键值数目都等于 m / 2 − 1 m/2-1 m/2−1,则就必须进行结点的“合并”,即把应删的键值删去后,将该结点中的剩余键值和指针连同父结点中指向该结点指针的左边(或右边)一个键值ki一起合并到左兄弟(或右兄弟)结点中,将ki从父结点中删去。如果因此使父结点中关键字数目< m / 2 − 1 m/2-1 m/2−1,则对此父结点做同样处理,以致于可能直到对根结点做这样的处理而使整个树减少一层。
- 如果因此使父结点中关键字数目< m / 2 − 1 m/2-1 m/2−1,则对此父结点做同样处理,以致于可能直到对根结点做这样的处理而使整个树减少一层。

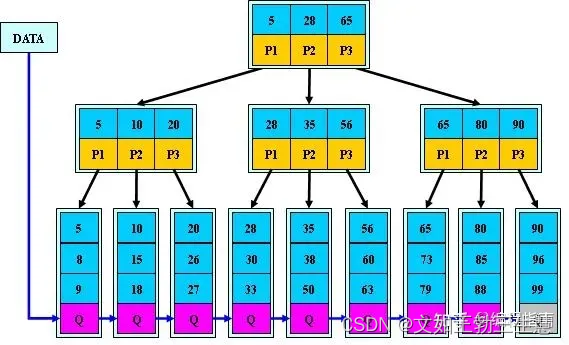
2.5 B+树
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别。
B+树是B树的变体,也是一种多路搜索树,其定义基本与B-树相同,除了:
1)非叶子结点的子树指针与关键字个数相同;
2)非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
3)为所有叶子结点增加一个链指针;
4)所有关键字都在叶子结点出现;
B+树的搜索与B树也基本相同,区别是B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找;
B+树的性质:
1.所有关键字都出现在叶子结点的链表中(稠密索引),且链表中的关键字恰好是有序的;
2.不可能在非叶子结点命中;
3.非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层;
4.更适合文件索引系统。
B+树比B树更适合操作系统的文件索引和数据库索引的原因:
B+树的磁盘读写代价更低,B+树的内部节点没有指向关键字具体信息的指针,因此内部节点相对B树更小。如果把所有同一内部节点的关键字放在同一块磁盘中,盘块所能容纳的关键字数量也就越多,一次性读入内存中的需要查找的关键字也就越多,相对IO读写次数降低。
B+树的查询效率更加稳定
由于非终结点并不是最终指向文件内容的结点,而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
所以,B+树只要遍历叶子节点就可以实现整棵树的遍历,支持基于范围的查询,而B树不支持range-query这样的操作(或者说效率太低)。
2.6 B*树
B∗树是B+树的变体,在B+树的非根和非叶子结点再增加指向兄弟的指针,将结点的最低利用率从1/2提高到2/3。
B∗树定义了非叶子结点关键字个数至少为2/3M,即块的最低使用率为2/3(代替B+树的1/2);

B+树的分裂:
当一个结点满时,分配一个新的结点,并将原结点中1/2的数据复制到新结点,最后在父结点中增加新结点的指针;B+树的分裂只影响原结点和父结点,而不会影响兄弟结点,所以它不需要指向兄弟的指针;
B∗树的分裂:
当一个结点满时,如果它的下一个兄弟结点未满,那么将一部分数据移到兄弟结点中,再在原结点插入关键字,最后修改父结点中兄弟结点的关键字(因为兄弟结点的关键字范围改变了);如果兄弟也满了,则在原结点与兄弟结点之间增加新结点,并各复制1/3的数据到新结点,最后在父结点增加新结点的指针;
所以,B∗树分配新结点的概率比B+树要低,空间使用率更高。
特点
在B+树的基础上因其初始化的容量变大,使得节点空间使用率更高,而又存有兄弟节点的指针,可以向兄弟节点转移关键字的特性使得B*树额分解次数变得更少。
2.5 算法分析
| 查找方法 | 平均查找长度 | 失败查找长度 |
|---|---|---|
| 二叉排序树 | l o g 2 ( n ) log_2(n) log2(n) | n |
| 二叉平衡树 | l o g 2 ( n ) log_2(n) log2(n) | l o g 2 ( n ) log_2(n) log2(n) |
| 红黑树 | l o g 2 ( n ) log_2(n) log2(n) | $ n>> x > log_2(n)$含义是略差于二叉平衡树,但是远远好于二叉排序树 |
| B树 | ≤ l o g m ( n + 1 ) + f i n d ( m ) ≤log_m(n+1)+find(m) ≤logm(n+1)+find(m) | 1 + l o g m / 2 ( ( n + 1 ) / 2 ) + f i n d ( m ) 1+log_{m/2}((n+1)/2)+find(m) 1+logm/2((n+1)/2)+find(m) find(m)指的是在m个元素中的查找长度,m一般比较小,采用顺序查找即可 |
| B+树 | l o g m ( n + 1 ) + f i n d ( m ) log_m(n+1)+find(m) logm(n+1)+find(m) | 1 + l o g m / 2 ( ( n + 1 ) / 2 ) + f i n d ( m ) 1+log_{m/2}((n+1)/2)+find(m) 1+logm/2((n+1)/2)+find(m) find(m)指的是在m个元素中的查找长度,m一般比较小,采用顺序查找即可 |
3.哈希表查找
给定关键字key,用一个函数H(key)计算出元素地址,由此而得散列表(Hash表,哈希表),
其中函数H(key)称为散列函数
此函数值称为散列地址。
现实中,会出现k1≠k2但H(k1)=H(k2)的情况,称这种现象为冲突现象,k1,k2为同义词。
针对冲突——如何解决冲突呢?
- 构造好的散列函数,以免冲突(减少冲突)
- 妥善处理冲突
构造散列函数的基本方法
直接定址法
H(k)= k 或者 H(k)= ak+b (a,b为任意正整数)
除留余数法
H(k)= k % p 其中p≤m,m为数组规模的最大质数。
平方取中法
例:325在平方后取105625中间两位作为它的散列地址。
折叠法
如 身份证号码:40104198805061532
先进行分组:340 104 198 805 061 532
冲突处理方法
开放地址法
Hi(k)=(H(k) + di ) % m,i=1,2,…,q q<=m
- 线性探测法:Hi(k)=(H(k)+i)%m,m为表的规模最大质数;
- 二次探测法:Hi(k) = ( H(k) + i2 ) % m
- 伪随机数:Hi(k) = ( H(k) + random() ) % m
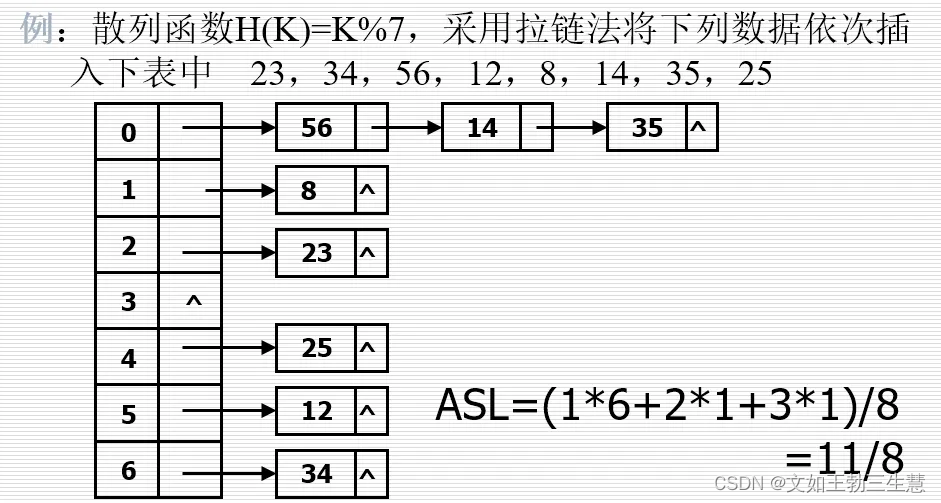
拉链法
将同义词构成一个链表
再散列法
→H(k)→H1(k)→H2(k)→ …… →Hi(k)
散列表的查找
在散列表中查找元素的过程和构造的过程基本一致:
对给定关键字k,由散列函数H计算出该元素的地址H(k)。
- 若表中该位置为空,则查找失败。
- 否则,比较关键字,若相等,查找成功,否则根据构造表时所采用的处理方法找下一个地址,直至找到关键字等于k的元素(成功)或者找到空位置(失败)为止。
一般在用拉链法构造的表中进行查找,比在用线性探测法构造的表中进行查找,查找长度要小。
3.1 算法分析
| 查找方法 | 平均查找长度 | 失败查找长度 |
|---|---|---|
| 哈希查找 | 1 | 1+m (哈希冲突用拉链法处理,命中的地址中链表长度为m) |
参考
https://www.cnblogs.com/kongxudeshenghuo/p/16174567.html
https://zhuanlan.zhihu.com/p/477346381
https://zhuanlan.zhihu.com/p/639905710
https://blog.csdn.net/Jay_fearless/article/details/119454973
https://zhuanlan.zhihu.com/p/659174741
https://zhuanlan.zhihu.com/p/666229978
相关文章:

查找算法及查找常用数据结构总结
1.顺序表查找 基本方法: 设查找表以一维数组来存储,要求在此表中查找出关键字的值为x的元素的位置,若查找成功,则返回其位置(即下标),否则,返回一个表示元素不存在的下标࿰…...
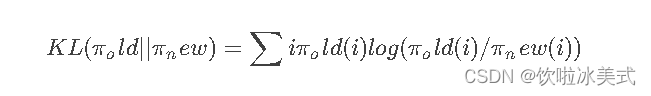
大语言模型---强化学习
本文章参考,原文链接:https://blog.csdn.net/qq_35812205/article/details/133563158 SFT使用交叉熵损失函数,目标是调整参数使模型输出与标准答案一致,不能从整体把控output质量 RLHF(分为奖励模型训练、近端策略优化…...

前端三剑客 —— CSS (第二节)
目录 内容回顾: CSS选择器*** 属性选择器 伪类选择器 1):link 超链接点击之前 2):visited 超链接点击之后 3):hover 鼠标悬停在某个标签上时 4):active 鼠标点击某个标签时,但没有松开 5):fo…...

牛客NC31 第一个只出现一次的字符【simple map Java,Go,PHP】
题目 题目链接: https://www.nowcoder.com/practice/1c82e8cf713b4bbeb2a5b31cf5b0417c 核心 Map参考答案Java import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*…...
01)
软考系统架构设计师(摘抄)01
架构师承担的责任 系统架构师设计师是承担系统架构设计的核心角色,他不仅是连接用户需求和系统进一步设计与实现的桥梁,也是系统开发早期阶段质量保证的关键角色。系统架构师就是项目的总设计师,他是一个既需要掌控整体又需要洞悉局部瓶颈&a…...
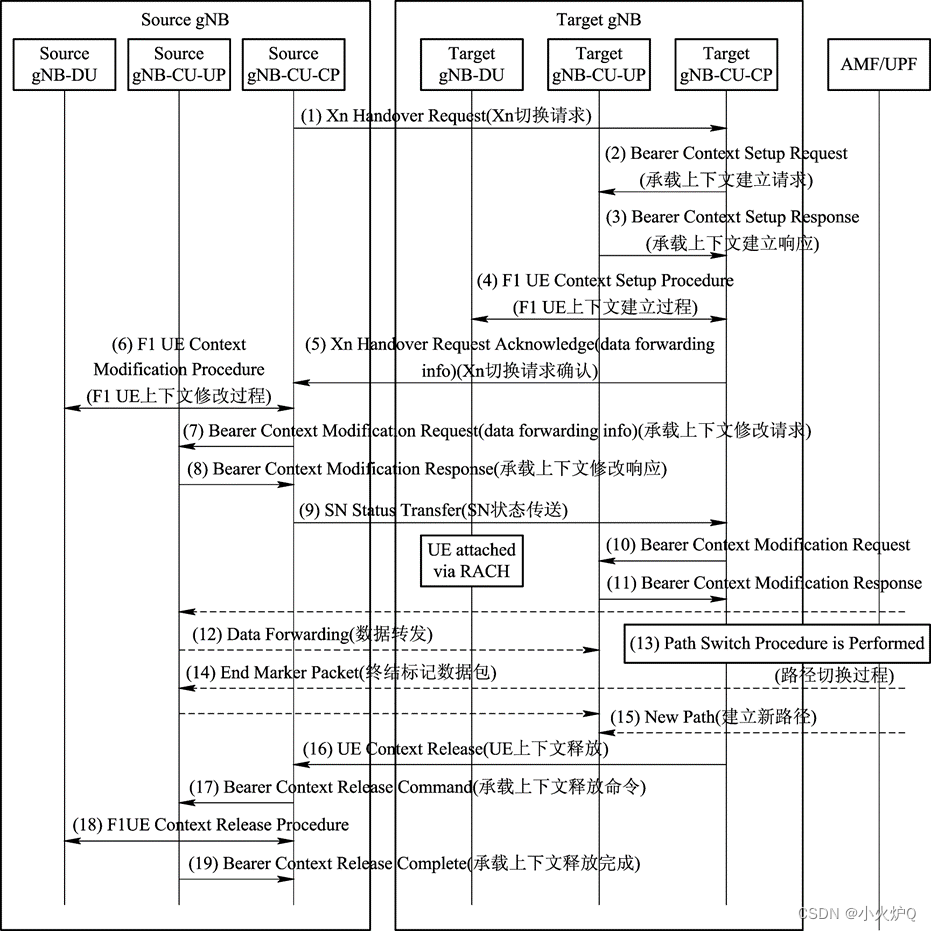
5G无线接入网和接口协议
**部分笔记** 4.3无线协议架构 NR无线协议分为两个平面:用户面和控制面。 用户面(UP):协议栈及用户数据采用的协议 控制面(Control Plane,CP)协议栈即系统的控制信令传输采用的协议簇。 虚线标注的是信令数据的流向。一个UE在…...

【力扣刷题日记】1173.即时食物配送I
前言 练习sql语句,所有题目来自于力扣(https://leetcode.cn/problemset/database/)的免费数据库练习题。 今日题目: 1173.即时食物配送I 表:Delivery 列名类型delivery_idintcustomer_idintorder_datedatecustomer…...

2024年github之node排行榜top50
如果有帮助到您还请动动手帮忙点赞,关注,评论转发,感谢啦!💕💕💕😘😘😘 本文由Butterfly一键发布工具发布 2024年github之node排行榜top50 语言star项目名称…...

当我们在地址栏输入URL的时候浏览器发生了什么
URL 解析 是否合法 首先判断你输入的是一个合法的 URL 还是一个待搜索的关键词,并且根据你输入的内容进行自动完成、字符编码等操作。检查http缓存 DNS 查询 浏览器缓存 -> 操作系统缓存 -> 路由器缓存 -> DNS缓存 -> 根域名服务器查询 TCP 连接 …...
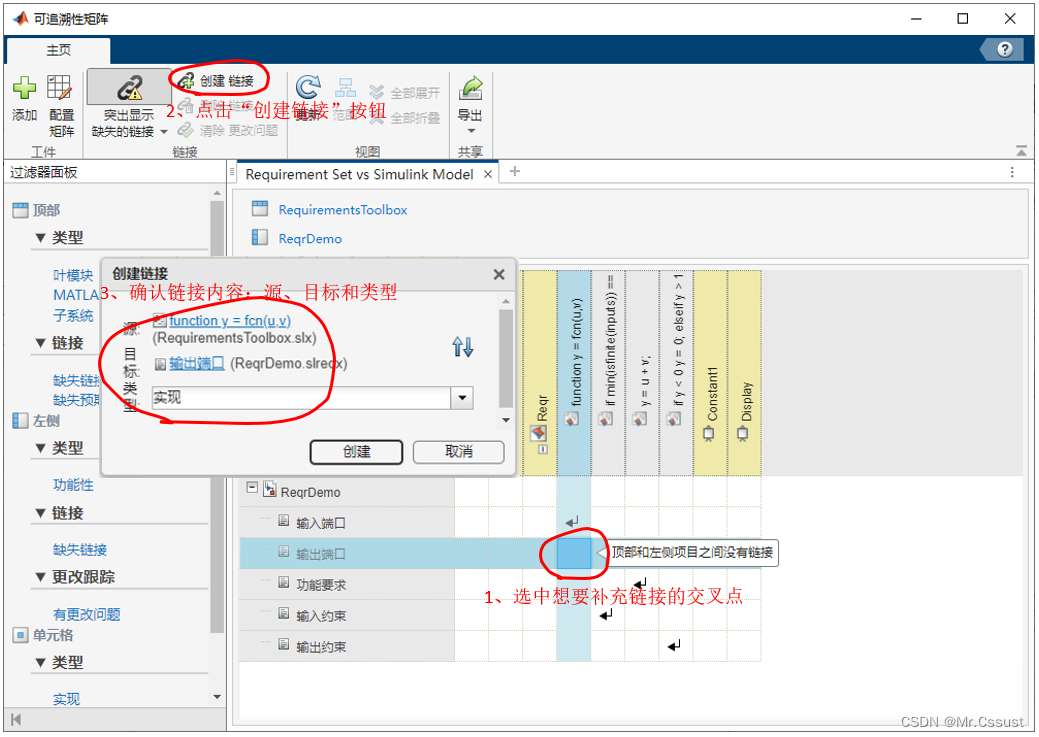
【研发日记】Matlab/Simulink开箱报告(十一)——Requirements Toolbox
目录 前言 Requirements Toolbox 编写需求 需求联接设计 需求跟踪开发进度 追溯性矩阵 分析和应用 总结 前言 见《开箱报告,Simulink Toolbox库模块使用指南(六)——S-Fuction模块(TLC)》 见《开箱报告&#x…...

Elastic 8.13:Elastic AI 助手中 Amazon Bedrock 的正式发布 (GA) 用于可观测性
作者:来自 Elastic Brian Bergholm 今天,我们很高兴地宣布 Elastic 8.13 的正式发布。 有什么新特性? 8.13 版本的三个最重要的组件包括 Elastic AI 助手中 Amazon Bedrock 支持的正式发布 (general availability - GA),新的向量…...
)
MFC 截取对话框生成图片、截取整个屏幕(可取黑白反色或者整体图片取反色)
HWND hwnd ::GetDesktopWindow();//截整个屏幕,用从这往下4句HDC hdc ::GetDC(hwnd);CDC dc;dc.Attach(hdc);CRect rc,rcw;GetWindowRect(&rcw);GetClientRect(&rc);//只截对话框,用这句//rc.SetRect(0, 0, GetSystemMetrics(SM_CXSCREEN), Ge…...

【LeetCode: 331. 验证二叉树的前序序列化 + DFS】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...
【Consul】Linux安装Consul保姆级教程
【Consul】Linux安装Consul保姆级教程 大家好 我是寸铁👊 总结了一篇【Consul】Linux安装Consul保姆级教程✨ 喜欢的小伙伴可以点点关注 💝 前言 今天要把编写的go程序放到linux上进行测试Consul服务注册与发现,那怎么样才能实现这一过程&am…...

pytorch常用的模块函数汇总(1)
目录 torch:核心库,包含张量操作、数学函数等基本功能 torch.nn:神经网络模块,包括各种层、损失函数和优化器等 torch.optim:优化算法模块,提供了各种优化器,如随机梯度下降 (SGD)、Adam、RMS…...
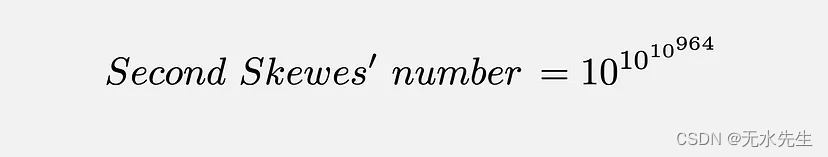
素数的计数律:Π函数、歪斜数
相当多的数字! 一、说明 自从人类开始掌握最起码的算术概念以来,有一类数字一直处于最前沿——素数。素数定义简单,但难以捕捉,众所周知,素数是数学中一些最困难问题的罪魁祸首,让几代最优秀的数学家感到…...

图像识别在农业领域的应用
图像识别技术在农业领域的应用正在逐渐成熟,它通过分析处理拍摄的植物或农田的图像,为农业生产提供决策支持。以下是图像识别在农业中的一些关键应用: 病虫害检测:图像识别技术能够识别作物上的病斑、虫害或异常状况。通过比较高…...
【JavaSE】java刷题--数组练习
前言 本篇讲解了一些数组相关题目(主要以代码的形式呈现),主要目的在于巩固数组相关知识。 上一篇 数组 讲解了一维数组和二维数组的基础知识~ 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎…...

预处理、编译、汇编、链接过程
预处理、编译、汇编、链接过程 预处理 引入头文件 #include 展开宏定义 #define 处理条件编译指令 #ifdef 删除注释 添加行号 在Linux下可以使用gcc -E命令把hello.c文件预处理成hello.i文件。windows这些操作都集成在编译器visual studio这些里面了。 编译 进行语法分…...

3、Cocos Creator 节点和组件
目录 1、 节点和组件 2、 节点层级和显示顺序 3、坐标系和节点变换属性 坐标系 锚点 旋转 缩放 尺寸 4、 常用技巧 5、参考 1、 节点和组件 Cocos Creator 的工作流程是以组件式开发为核心的,组件式架构也称作 组件 — 实体系统(或 Entity-C…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
