红黑树介绍及插入操作的实现
🎉个人名片:
🐼作者简介:一名乐于分享在学习道路上收获的大二在校生
🙈个人主页🎉:GOTXX
🐼个人WeChat:ILXOXVJE
🐼本文由GOTXX原创,首发CSDN🎉🎉🎉
🐵系列专栏:零基础学习C语言----- 数据结构的学习之路----C++的学习之路
🐓每日一句:如果没有特别幸运,那就请特别努力!🎉🎉🎉
————————————————
文章目录
- 1.红黑树的概念
- 2 红黑树的性质
- 3 红黑树节点的定义
- 4.红黑树的插入操作(分类详解)
- 5.红黑树与AVL树的比较
1.红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

2 红黑树的性质
性质:
- 每个结点不是红色就是黑色
- 根节点是黑色的
- 如果一个节点是红色的,则它的两个孩子结点是黑色的
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)
思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
首先,要满足黑色节点数目相同,则当只有黑色节点的时候,路径最短,因为红色节点不能连续出现,所以当黑色节点与红色节点交替的时候,路径最长,并且为最短的两倍。
3 红黑树节点的定义
enum color //颜色
{RED,BLACK
};
template<class K, class V>
struct AVLNode
{AVLNode<K, V>* _left;AVLNode<K, V>* _right;AVLNode<K, V>* _parent;pair<K, V> _kv;color _col; //记录节点颜色AVLNode(pair<K, V>& kv) :_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED) //新节点的颜色默认为红色{}
};
新插入节点的颜色为红色的原因?
原因:因为红黑树有一条规则,就是每条路径的黑色节点数目相等,插入前每条路径的黑色数目是相等的,但是如果插入的是黑色节点的话,那么该条路径的黑色节点的数目就多了一个,直接违反规则,所以插入新节点为红色节点;
4.红黑树的插入操作(分类详解)
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
- 按照二叉搜索的树规则插入新节点
- 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;
但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:
含义解析:
cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
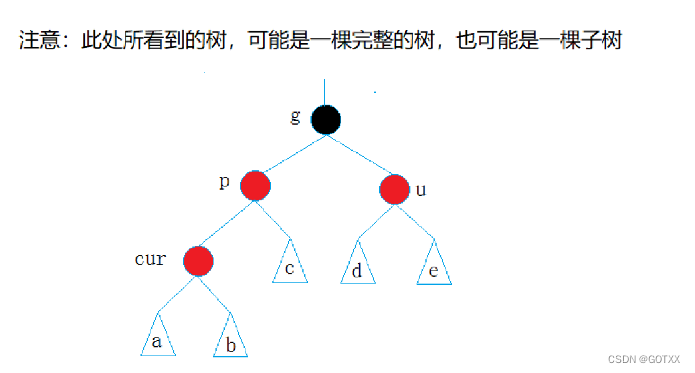
情况一:cur为红色,p为红色,g为黑色,u存在并且为红色
根据上图进行分析:
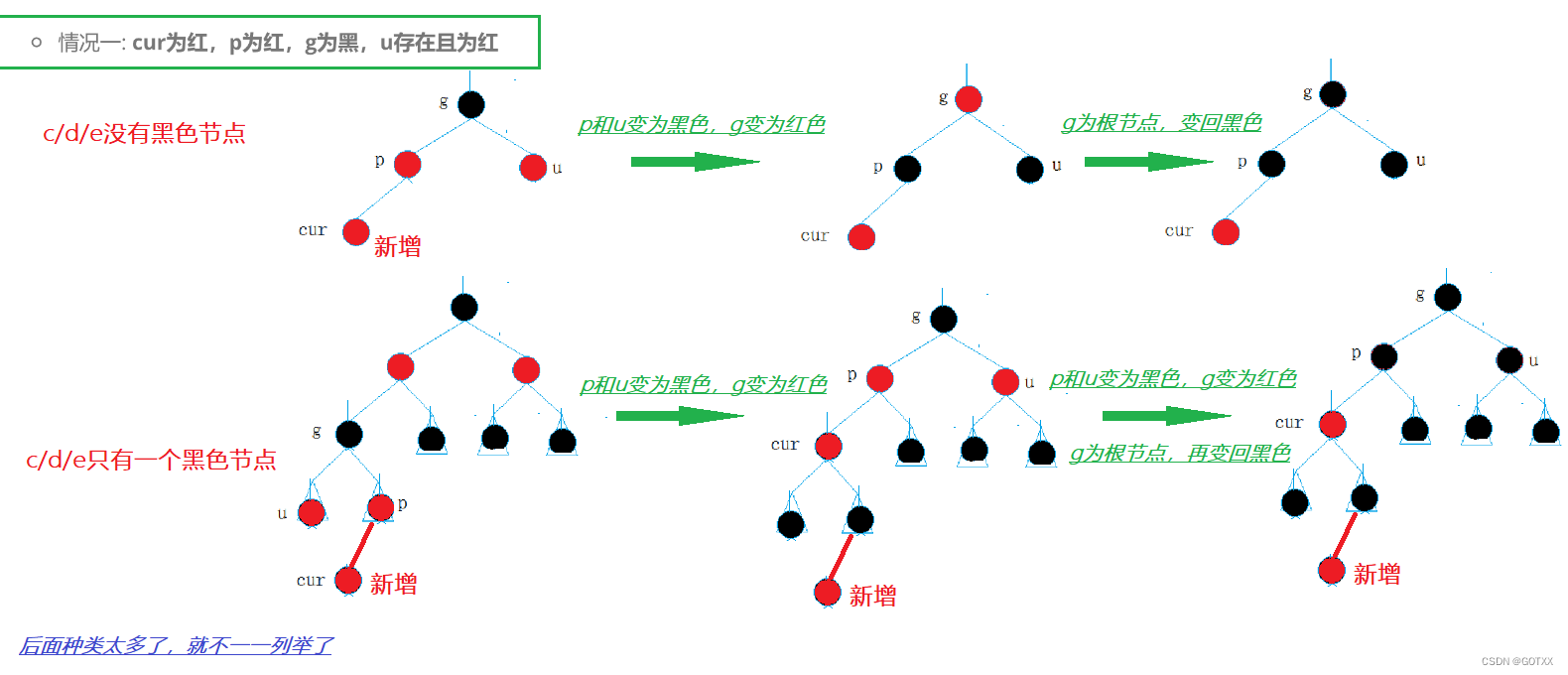
解析:
这里p与cur都为红色,违反规则,我们不能直接将p的颜色改为黑色,如果直接改为黑色的话,则每条路径的黑色节点数目就变化了,违反规则。
我们应该将p与u变为红色,g变为黑色,如果g是子树,还需向上调整(比如上图中的下面一种情况),如果g是根节点,则需要变回黑色,因为规则里根节点必须为黑色;
代码实现
//这里是一个while循环,只展示了循环体里面的代码//情况一:uncle存在并且为红色if (uncle && uncle->_col == RED){uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;parent = grandfather; //如果为子树,则继续向上调整cur = parent; if (_root == grandfather) //如果g为根节点,则改回黑色{grandfather->_col = BLACK;}}
情况二:u不存在或则u存在并且为黑色
下面的分类与AVL树的旋转的分类很类似;
分析一:u不存在/存在且黑色,并且p为g的左,c为p的左 或则 p为g的右,c为p的右(p,g,c在一条线上)
当u不存在时:处理方法:单旋+变色
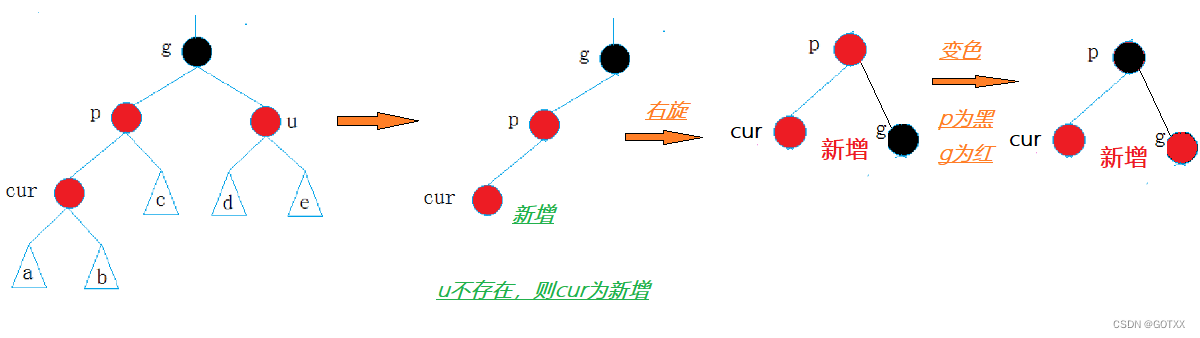
当u存在时:处理方法:也是单旋+变色
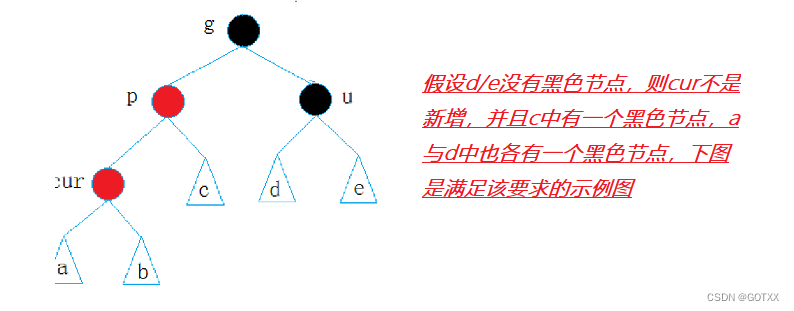
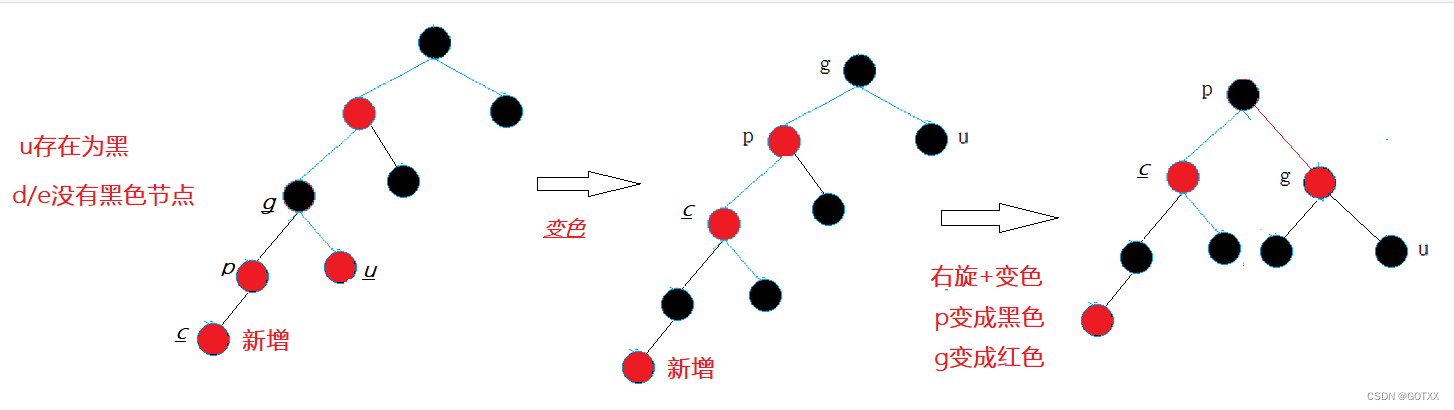
总结:
当u存在为黑色或则不存在时,都需要旋转+变色(这里的旋转与上章AVL旋转一样)
如果c为p的左,并且p为g的左,则右旋
如果c为p的右,并且p为g的右,则左旋
变色: 都是p变成黑色,g变为红色
代码实现
//p为g左,c为p左
if (parent==grandfather->_left && cur==parent->_left)
{ rotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;
}
//p为g右,c为p右
else if (parent == grandfather->_right && cur == parent->_right)
{rotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;
}
分析三:u不存在或则存在为黑色,但是p为g的左,c为p的右边 或则 p为g的右,c为p的左(p,g,c不在一条线上)
当u不存在时:处理方法:双旋+变色
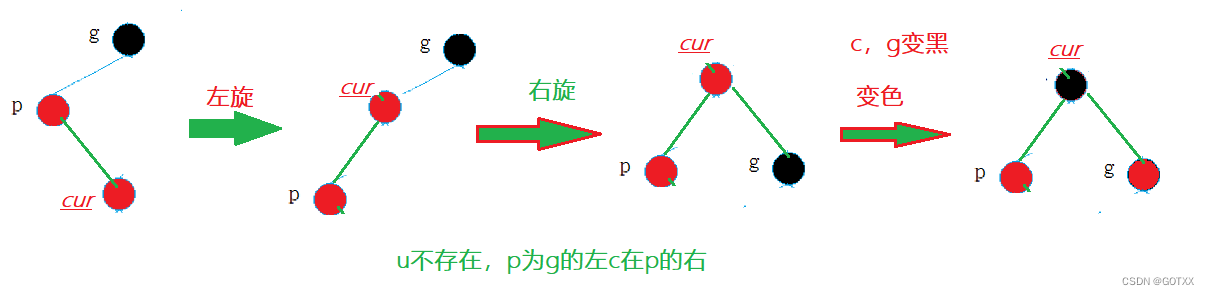
当u存在时:处理方法:双旋+变色
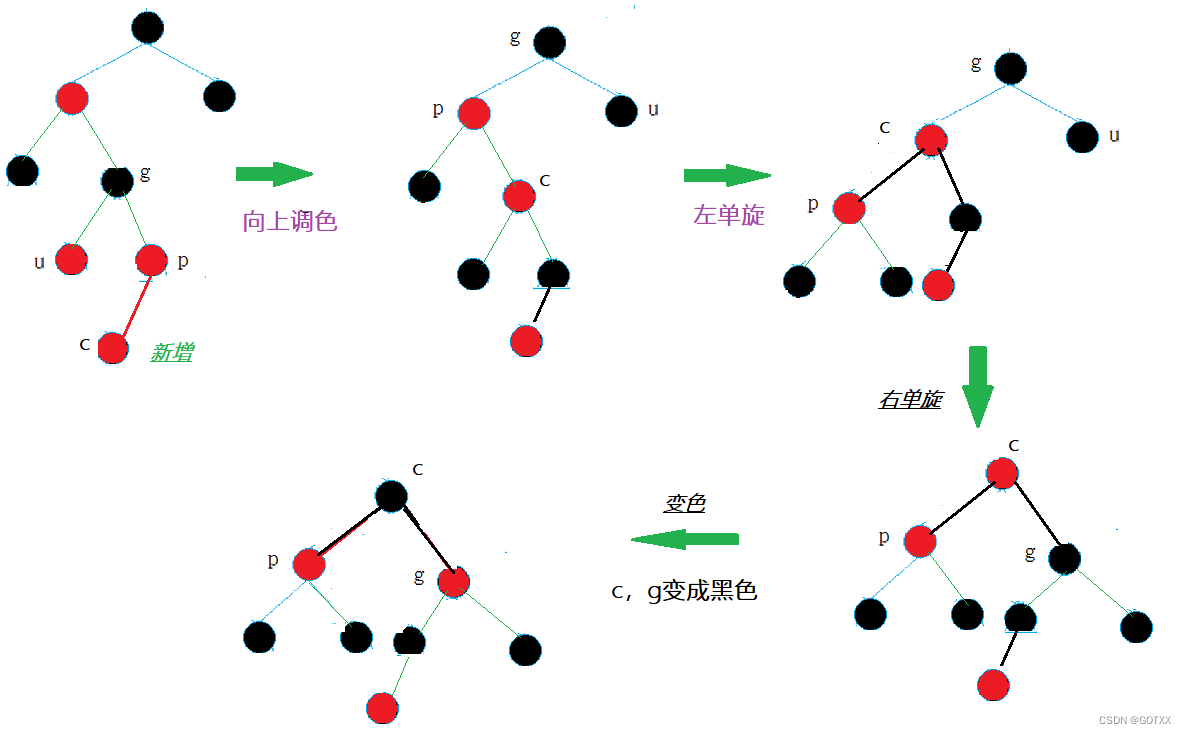
总结:
当g,p,c不在一条街直线上时,需要双旋+变色处理
旋转方向的判定和AVL树的旋转一样;(上章讲过)
代码实现:
//一左一右
else if(parent == grandfather->_left && cur == parent->_right)
{rotateL(parent);rotateR(grandfather);cur->_col = BLACK;parent->_col = BLACK;break;
}
else if (parent == grandfather->_right && cur == parent->_left)
{rotateR(parent);rotateL(grandfather);cur->_col = BLACK;parent->_col = BLACK;break;
}
插入总代码
bool insert(pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;}//找插入点Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv > kv){parent = cur;cur = cur->_left;}else if (cur->_kv < kv){parent = cur;cur = cur->_right;}else{return false;}}//插入if (cur == parent->left){cur = new Node(kv);parent->_left = cur;cur->_parent = parent;}else if (cur == parent->right){cur = new Node(kv);parent->_right = cur;cur->_parent = parent;}//调节颜色/调节使其满足规则while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent = grandfather->_left){Node* uncle = grandfather->_right;}else{Node* uncle = grandfather->_left;}//情况一:uncle存在并且为红色if (uncle && uncle->_col == RED){uncle->_col = BLACK;parent->_col = BLACK;grandfather->_col = RED;parent = grandfather; //如果为子树,则继续向上调整cur = parent; if (_root == grandfather) //如果g为根节点,则改回黑色{grandfather->_col = BLACK;}}//uncle不存在或则存在为黑色else{//p为g左,c为p左if (parent==grandfather->_left && cur==parent->_left){ rotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}//p为g右,c为p右else if (parent == grandfather->_right && cur == parent->_right){rotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;break;}//一左一右else if(parent == grandfather->_left && cur == parent->_right){rotateL(parent);rotateR(grandfather);cur->_col = BLACK;parent->_col = BLACK;break;}else if (parent == grandfather->_right && cur == parent->_left){rotateR(parent);rotateL(grandfather);cur->_col = BLACK;parent->_col = BLACK;break;}}}
}
//左单旋
void rotateL(Node* parent)
{Node* pparent = parent->_parent; //记录所旋转根节点的父亲Node* pNodeR = parent->_right;Node* pNodeRL = pNodeR->_left;if (pNodeRL) //如果该旋转节点的右节点的左孩子存在parent->_right = pNodeRL;pNodeR->_left = parent;//新的父节点的链接if (parent == _root){_root = pNodeR;pparent = nullptr;}else{if (pparent->_left == parent){pparent->_left = pNodeR;}else{pparent->_right = pNodeR;}}
}
//右单旋
void rotateR(Node* parent)
{Node* pparent = parent->_parent;Node* pNodeL = parent->_left;Node* pNodeLR = pNodeL->_right;if (pNodeLR)parent->_left = pNodeLR;pNodeL->_right = parent;if (parent == _root){_root = pNodeL;pparent = nullptr;}else{if (pparent->_left == parent){pparent->_left = pNodeL;}else{pparent->_right = pNodeL;}}
}
5.红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
相关文章:

红黑树介绍及插入操作的实现
🎉个人名片: 🐼作者简介:一名乐于分享在学习道路上收获的大二在校生 🙈个人主页🎉:GOTXX 🐼个人WeChat:ILXOXVJE 🐼本文由GOTXX原创,首发CSDN&…...

[linux初阶][vim-gcc-gdb] TwoCharter: gcc编译器
目录 一.Linux中gcc编译器的下载与安装 二.使用gcc编译器来翻译 C语言程序 ①.编写C语言代码 ②翻译C语言代码 a.预处理 b.编译 c.汇编 d.链接 ③.执行Main 二进制可执行程序(.exe文件) 三.总结 一.Linux中gcc编译器的下载与安装 使用yum命令(相当于手机上的应用…...
)
单例设计模式(2)
单例设计模式(2) 单例模式存在的问题 单例对 OOP 特性的支持不友好 oop的特性:封装、继承、多态、抽象;以Id生成器代码为例,如果未来某一天,我们希望针对不同的业务采用不同的 ID 生成算法。比如&#x…...
队列支持)
boost::asio 启用 io_uring(Linux 5.10)队列支持
欲启用 boost::asio 对于 io_uring 的支持,这需要以下几个先决条件; 1、boost 1.78 及以上发行版本 Revision History - 1.78.0 (boost.org) 2、Linux kernel 5.10 及以上发行版本 3、在预定义头文件(stdafx.h)、或编译器预定义…...
Android 自定义坐标曲线图(二)
Android 自定义坐标曲线图_android 自定义曲线图-CSDN博客 继上一篇文章,点击折线图上的点,显示提示信息进行修改,之前通过回调,调用外部方法,使用popupwindow或dialog来显示,但是这种方法对于弹框显示的位…...

每日OJ题_子序列dp⑧_力扣446. 等差数列划分 II - 子序列
目录 力扣446. 等差数列划分 II - 子序列 解析代码 力扣446. 等差数列划分 II - 子序列 446. 等差数列划分 II - 子序列 难度 困难 给你一个整数数组 nums ,返回 nums 中所有 等差子序列 的数目。 如果一个序列中 至少有三个元素 ,并且任意两个相邻…...

GOPROXY 代理设置
通常报错: 1.http: server gave HTTP response to HTTPS client 2.timeout 解决指令:(会话临时性),长久的可以在配置文件中配置 go env -w GOPROXYhttps://goproxy.cn,direct 长久的,在~/.bashrc文件中添加: expo…...

Redis面经
Redis面经 Redis缓存穿透、缓存击穿和缓存雪崩及解决方案概述缓存穿透详解及解决方案缓存击穿详解及解决方案缓存雪崩详解及解决方案 Redis持久化机制什么是数据持久化?Redis数据持久化概述RDB持久化的优缺点AOF持久化混合持久化 Redis缓存穿透、缓存击穿和缓存雪崩…...
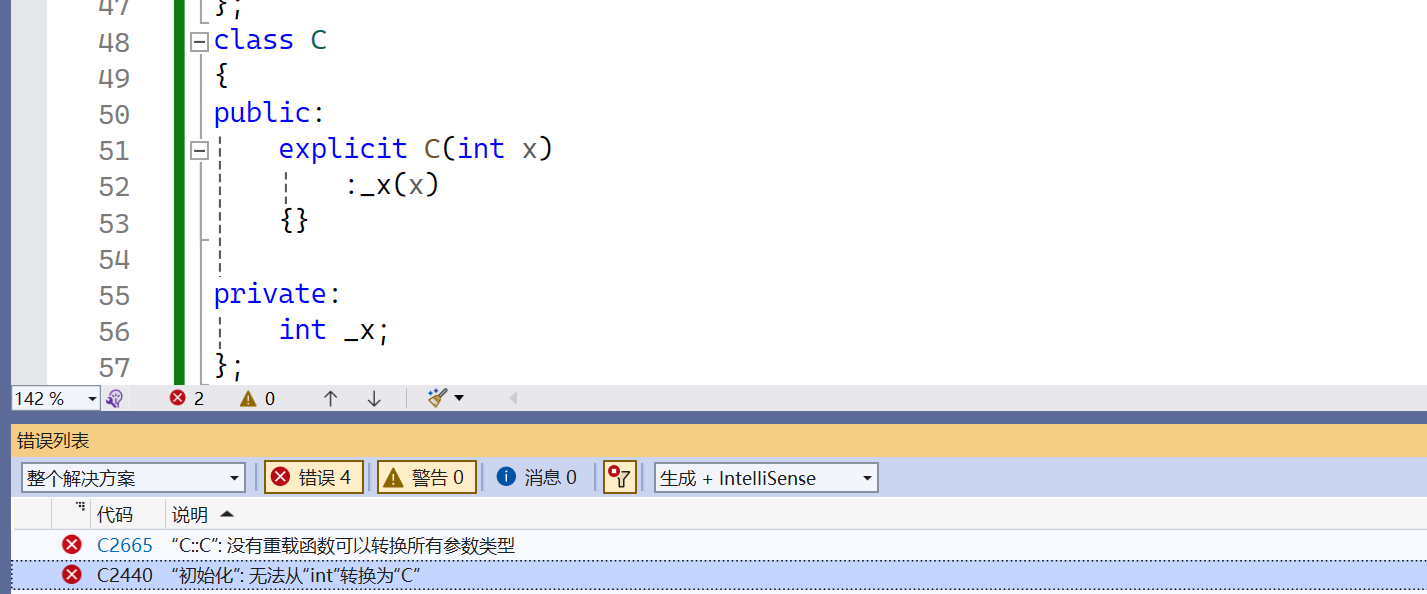
【c++】类和对象(六)深入了解隐式类型转换
🔥个人主页:Quitecoder 🔥专栏:c笔记仓 朋友们大家好,本篇文章我们来到初始化列表,隐式类型转换以及explicit的内容 目录 1.初始化列表1.1构造函数体赋值1.2初始化列表1.2.1隐式类型转换与复制初始化 1.3e…...

什么是nginx正向代理和反向代理?
什么是代理? 代理(Proxy), 简单理解就是自己做不了的事情或实现不了的功能,委托别人去做。 什么是正向代理? 在nginx中,正向代理指委托者是客户端,即被代理的对象是客户端 在这幅图中,由于左边内网中…...

【Go】面向萌新的Gin框架知识梳理学习笔记
目录 Gin框架简介 路由&路由组 1. 定义基本路由 2. 参数传递 3. 查询字符串参数 4. 路由组 5. 路由中间件 模板渲染 1. 加载模板 2. 定义模板 3. 渲染模板 4. 自定义模板函数 返回json 1. 导入 Gin 包 2. 创建 Gin 引擎 3. 定义路由和处理器函数 4. 运行服…...

baseDao增删改查.
这里写目录标题 1、baseDao增删改查介绍2、basDao类3、BasDao类的作用 1、baseDao增删改查介绍 (1)、增加Create)操作: 通过BaseDao的insert方法可以向数据库中插入一条新的记录。 该方法接受一个实体对象作参数,将该对象的属性映射到表的字…...

什么是面向对象【大白话Java面试题】
什么是面向对象 同样是解决一个问题,面向对象的角度是将问题抽象成对象的形式。通过分类的思维方式,将问题分成几个解决方案的对象。给每个对象赋值属性和方法,对每个对象的细节进行面向过程的思维,执行自己的方法来解决问题。 …...
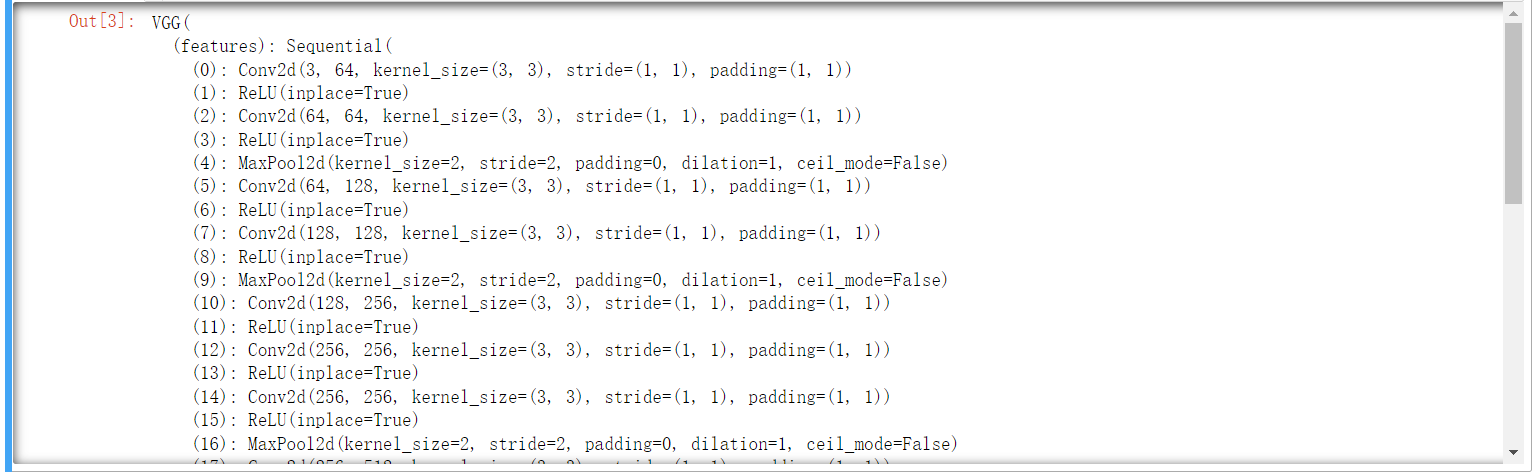
PyTorch 教程-快速上手指南
文章目录 PyTorch Quickstart1.处理数据2.创建模型3.优化模型参数4.保存模型5.加载模型 PyTorch 基础入门1.Tensors1.1初始化张量1.2张量的属性1.3张量运算1.3.1张量的索引和切片1.3.2张量的连接1.3.3算术运算1.3.4单元素张量转变为Python数值 1.4Tensor与NumPy的桥接1.4.1Tens…...

【有芯职说】数字芯片BES工程师
一、 数字芯片BES工程师简介 今天来聊聊数字芯片BES工程师,其中BES是Back End Support的缩写,就是后端支持的意思。其实这个岗位是数字IC前端设计和数字IC后端设计之间的一座桥,完成从寄存器传输级设计到具体工艺的mapping和实现。这个岗位在…...
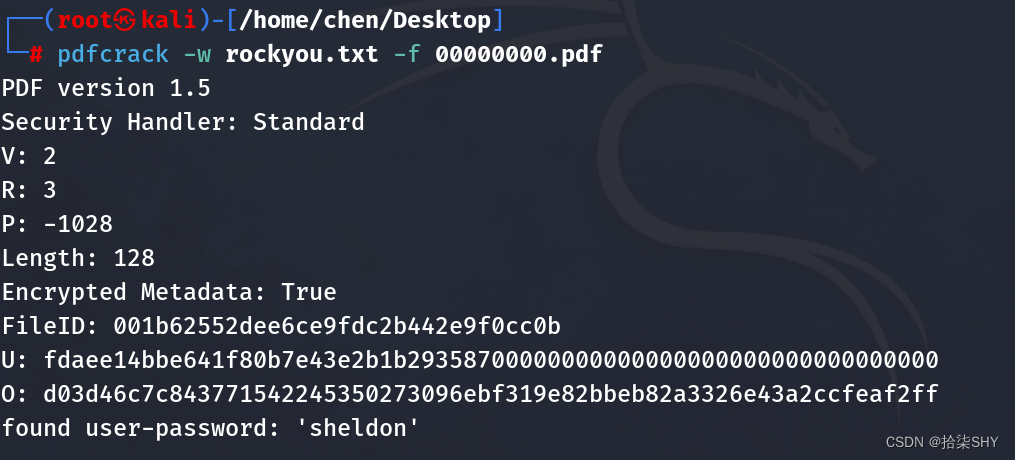
暴力破解pdf文档密码
首先安装pdfcrack工具包 apt install pdfcrack 默认密码字典存储在/usr/share/wordlists里,是gz文件,将它解压并copy到pdf目录 然后使用pdfcrack破解 密码在最后一行user-password的单引号里...

蓝桥杯刷题第四天
思路: 这道题很容易即可发现就是简单的暴力即可完成题目,我们只需满足所有数的和为偶数即可保证有满足条件的分法,同时也不需要存下每个输入的数据,只需要知道他是偶数还是奇数即可,因为我们只需要偶数个奇数搭配在一块…...

03-数据库的用户管理
一、创建新用户 mysql> create user xjzw10.0.0.% identified by 1; Query OK, 0 rows affected (0.01 sec) 二、查看当前数据库正在登录的用户 mysql> select user(); ---------------- | user() | ---------------- | rootlocalhost | ---------------- 1 row …...

每日一题 --- 三数之和[力扣][Go]
三数之和 题目:15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 **注意&#x…...
)
vue render 函数详解 (配参数详解)
vue render 函数详解 (配参数详解) 在 Vue 3 中,render 函数被用来代替 Vue 2 中的模板语法。 它接收一个 h 函数(或者是 createElement 函数的别名),并且返回一个虚拟 DOM。 render 函数的语法结构如下: render(h) …...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...
