数据分析之Tebleau 简介、安装及数据导入
Tebleau简介
Tebleau基于斯坦福大学突破性交互式技术
可以将结构化数据快速生成图表、坐标图、仪表盘与报告
将维度拖放到画布等地方是他的主要操作方式
例:Tebleau是手机相机 (相对来说更简单) POWER BI是单反相机
Tebleau各类产品
- Tebleau Desktop(是收费的)
个人版能连接的数据源是有限的
专业版几乎能连接所有格式或类型的数据文件或数据库
专业版能与Tebleau Server相连,个人版不能
- Tebleau Server
用于发布和管理Tebleau Desktop制作的仪表板和数据源,需要架设一台服务器,收集大家的报表。当仪表盘发送到server上,其他同事可以通过浏览器或平板看到
- Tebleau online
与Tebleau Server是一样的,只是云端的
- Tebleau public (免费的)
数据源的选取保存和发布有一定的限制
- Tebleau reader
用来看别人做的Tebleau 视图
-
下载Tebleau public 地址
https://www.tableau.com/zh-cn/products/public
-
导入数据源-连接excel和CSV数据源
先导入一个excel文件
在导入一个文本文件(可以和第一个一样导入,也可以直接添加)
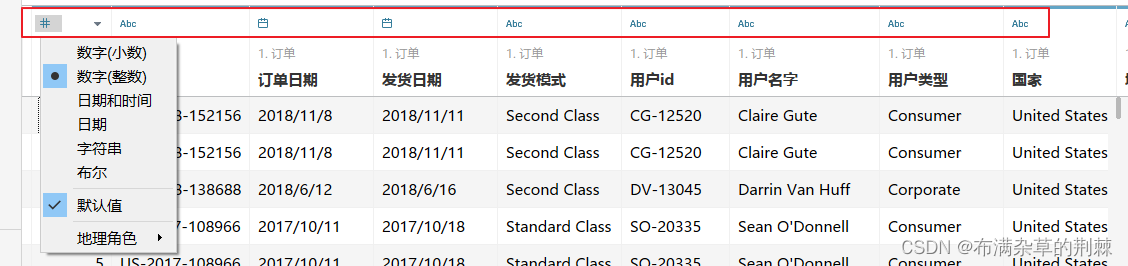
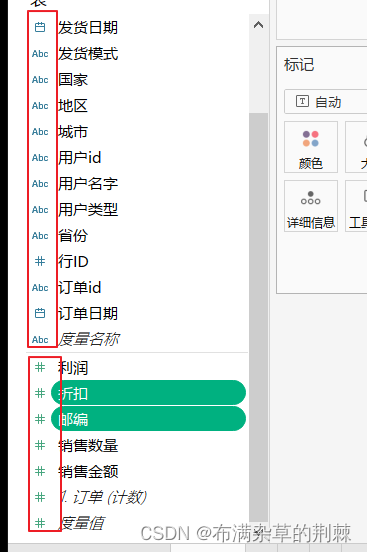
导入数据中的三张表
上面的不同的名字代表不同的类型
右边有一个可以显示的行数(可自定义)
进入到转到工作表界面,开始做图
横线前面是维度,横线后面是数值
-
开始做图
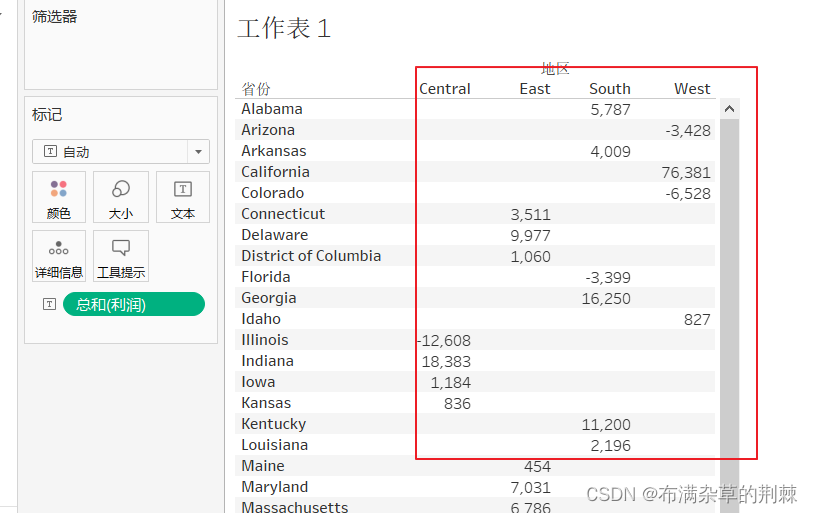
将省份拖入行,地区拖入列,下面还没有显示数据,只是显示了相应的数据类型
可以直接将利润拖入这边的表格中
可以对应修改右边的图表
-
在线的资源库
https://public.tableau.com/app/learn/how-to-videos
相关文章:

数据分析之Tebleau 简介、安装及数据导入
Tebleau简介 Tebleau基于斯坦福大学突破性交互式技术 可以将结构化数据快速生成图表、坐标图、仪表盘与报告 将维度拖放到画布等地方是他的主要操作方式 例:Tebleau是手机相机 (相对来说更简单) POWER BI是单反相机 Tebleau各类产品 Teblea…...

分享一下设计模式的学习
分享一下设计模式的学习 1、什么是设计模式? 设计模式是在软件设计过程中,经过实践和总结得出的描述、解决软件设计问题的一种经验总结。它是一种被广泛接受和验证的最佳实践,用于解决特定类型的问题,并提供了可重用的解决方案。…...

【JavaEE初阶系列】——CAS
目录 🎈什么是 CAS 📝CAS 伪代码 🎈CAS 是怎么实现的 🎈CAS 有哪些应用 🚩实现原子类 🌈伪代码实现: 🚩实现自旋锁 🌈自旋锁伪代码 🎈CAS 的 ABA 问题 &#…...

webGIS 之 智慧校园案例
1.引入资源创建地图 //index.html <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content&qu…...

CVAE——生成0-9数字图像(Pytorch+mnist)
1、简介 CVAE(Conditional Variational Autoencoder,条件变分自编码器)是一种变分自编码器(VAE)的变体,用于生成有条件的数据。在传统的变分自编码器中,生成的数据是完全由潜在变量决定的&…...

【Linux】TCP网络套接字编程+守护进程
文章目录 日志类(完成TCP/UDP套接字常见连接过程中的日志打印)单进程版本的服务器客户端通信多进程版本和多线程版本守护进程化的多线程服务器 日志类(完成TCP/UDP套接字常见连接过程中的日志打印) 为了让我们的代码更规范化&…...

【Qt 学习笔记】Day2 | 认识QtSDK中的重要工具
博客主页:Duck Bro 博客主页系列专栏:Qt 专栏关注博主,后期持续更新系列文章如果有错误感谢请大家批评指出,及时修改感谢大家点赞👍收藏⭐评论✍ Day2 | 认识QtSDK中的重要工具 文章编号:Qt 学习笔记 / 03…...

adc123456
DMA主要用于协助CPU完成数据转运的工作 DMA,英文全称Direct Memory Access,DMA这个外设是可以直接访问STM32内部存储器的,包括运行内存SRAM,程序存储器flash和寄存器等等,DMA都有权限访问,所以DMA能完成数据…...

YOLOV5训练自己的数据集教程(万字整理,实现0-1)
文章目录 一、YOLOV5下载地址 二、版本及配置说明 三、初步测试 四、制作自己的数据集及转txt格式 1、数据集要求 2、下载labelme 3、安装依赖库 4、labelme操作 五、.json转txt、.xml转txt 六、修改配置文件 1、coco128.yaml->ddjc_parameter.yaml 2、yolov5x.…...
精通Go语言文件上传:深入探讨r.FormFile函数的应用与优化
1. 介绍 1.1 概述 在 Web 开发中,文件上传是一项常见的功能需求,用于允许用户向服务器提交文件,如图像、文档、视频等。Go 语言作为一门强大的服务器端编程语言,提供了方便且高效的方式来处理文件上传操作。其中,r.F…...

【C语言】字符串
C语言用字符数组存放字符串,字符数组中的各元素依次存放字符串的各字符 一维字符数组:存放一个字符串(每个数组元素存放一个字符)二维字符数组:存放多个一维数组(字符串);二维数组的…...

云计算探索-DAS、NAS与SAN存储技术演进及其应用比较
1,介绍 随着信息技术的飞速发展,数据存储的需求日益增长,各种存储技术也应运而生。在众多的存储解决方案中,直接附加存储(Direct Attached Storage,简称DAS)、网络附加存储(Network …...
手机有线投屏到直播姬pc端教程
1 打开哔哩哔哩直播姬客户端并登录(按下图进行操作) 2 手机用usb数据线连接电脑(若跳出安装驱动的弹窗点击确定或允许),usb的连接方式为仅充电(手机差异要求为仅充电),不同品牌手机要求可能不一样,根据实际的来 3 在投屏过程中不要更改usb的连接方式(不然电脑会死机需要重启) …...

SOA、分布式、微服务之间的关系?
分布式它本身就是一种系统部署的架构理念,意思就是将一个系统拆分为各个部分,然后分别部署到不同的机器上去,SOA和微服务项目的部署方式都可以是分布式架构。 而SOA和微服务它们都是面向服务的架构,但是微服务相比于SOA在服务粒度…...
)
Java多线程学习(概念笔记)
面试题:并行和并发有什么区别? 现在都是多核CPU,在多核CPU下 并发是同一时间应对多件事情的能力,多个线程轮流使用一个或多个CPU 并行是同一时间动手做多件事情的能力,4核CPU同时执行4个线程 面试题:创建线…...
【C++】set和map
set和map就是我们上篇博客说的key模型和keyvalue模型。它们属于是关联式容器,我们之前说过普通容器和容器适配器,这里的关联式容器就是元素之间是有关联的,通过上篇博客的讲解我们也对它们直接的关系有了一定的了解,那么下面我们先…...
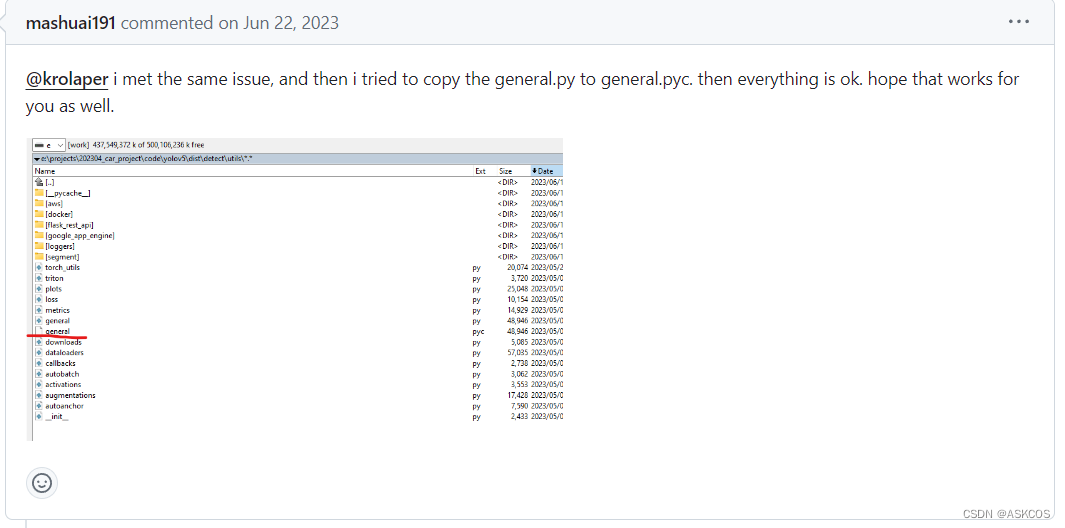
yolov5 v7.0打包exe文件,使用C++调用
cd到yolo5文件夹下 pyinstaller -p 当前路径 -i logo图标 detect.py问题汇总 运行detect.exe找不到default.yaml 这个是yolov8里的文件 1 复制权重文件到exe所在目录。 2 根据报错提示的配置文件路径,把default.yaml复制放到相应的路径下。(缺少相应…...

保研线性代数机器学习基础复习2
1.什么是群(Group)? 对于一个集合 G 以及集合上的操作 ,如果G G-> G,那么称(G,)为一个群,并且满足如下性质: 封闭性:结合性:中性…...
vultr ubuntu 服务器远程桌面安装及连接
一. 概述 vultr 上开启一个linux服务器,都是以终端形式给出的,默认不带 ui 桌面的,那其实对于想使用服务器上浏览器时的情形不是很好。那有没有方法在远程服务器安装桌面,然后原程使用呢?至少ubuntu的服务器是有的&am…...
前端学习<二>CSS基础——12-CSS3属性详解:动画详解
前言 本文主要内容: 过渡:transition 2D 转换 transform 3D 转换 transform 动画:animation 过渡:transition transition的中文含义是过渡。过渡是CSS3中具有颠覆性的一个特征,可以实现元素不同状态间的平滑过渡…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...