数据挖掘|贝叶斯分类器及其Python实现
分类分析|贝叶斯分类器及其Python实现
- 0. 分类分析概述
- 1. Logistics回归模型
- 2. 贝叶斯分类器
- 2.1 贝叶斯定理
- 2.2 朴素贝叶斯分类器
- 2.2.1 高斯朴素贝叶斯分类器
- 2.2.2 多项式朴素贝叶斯分类器
- 2.3 朴素贝叶斯分类的主要优点
- 2.4 朴素贝叶斯分类的主要缺点
- 3. 贝叶斯分类器在生产中的应用
- 4. 朴素贝叶斯分类器的Python实现
- 5. 贝叶斯分类器和Logistic回归分类边界的对比
- 6. 空气污染的分类预测
0. 分类分析概述
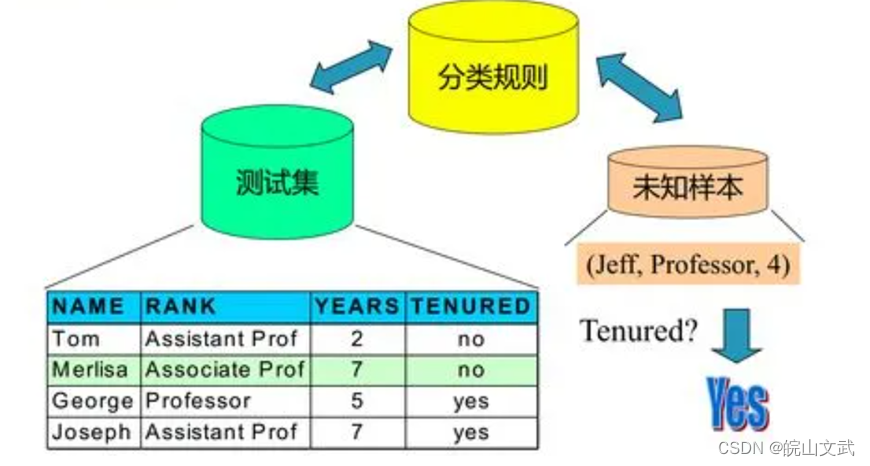
分类是数据挖掘的主要方法,通过有指导的学习训练建立分类模型。
分类的目的是通过学习,得到一个分类函数或分类模型(也常常称作分类器),该模型能够把数据集中的对象映射到给定类别中的某一个类上。
分类和回归都属于预测建模,分类用于预测可分类属性或变量,而回归用于预测连续的属性取值。
1. Logistics回归模型
最常见的分类预测模型为:
l o g ( P 1 − P ) = β 0 + β 1 X 1 + β 2 X 2 + . . . + β p X p + ε log(\frac{P}{1-P})=\beta_0+\beta_1X_1+\beta_2X_2+...+\beta_pX_p+\varepsilon log(1−PP)=β0+β1X1+β2X2+...+βpXp+ε
该模型被称为Logistics回归模型,适用于输出变量仅有0、1两个类别(或分类)值的二分类预测。例如:基于顾客的购买行为预测其是否会参加本次对该类商品的促销。
2. 贝叶斯分类器
在实际应用中,样本的属性集与类别的关系一般是不确定的,但可能存在一种概率关系。贝叶斯分类器是一种基于统计概率的分类器,通过比较样本术语不同类别的概率大小对其进行分类。
这里对朴素贝叶斯分类器进行介绍,朴素贝叶斯分类器是贝叶斯定理(一种样本属性集与类别的概率关系建模方法)的实现。
2.1 贝叶斯定理
假设 X X X和 Y Y Y在分类中可以分别表示样本的属性集和类别。 p ( X , Y ) p(X,Y) p(X,Y)表示它们的联合概率, p ( X ∣ Y ) p(X|Y) p(X∣Y)和 p ( Y ∣ X ) p(Y|X) p(Y∣X)表示条件概率,其中 p ( Y ∣ X ) p(Y|X) p(Y∣X)是后验概率,而 p ( Y ) p(Y) p(Y)称为 Y Y Y的先验概率。 X X X和 Y Y Y的联合概率和条件概率满足下列关系:
p ( X , Y ) = p ( Y ∣ X ) p ( X ) = p ( X ∣ Y ) p ( Y ) p(X,Y)=p(Y|X)p(X)=p(X|Y)p(Y) p(X,Y)=p(Y∣X)p(X)=p(X∣Y)p(Y)
变换后得到:
p ( Y ∣ X ) = p ( X ∣ Y ) p ( Y ) p ( X ) p(Y|X)=\frac {p(X|Y)p(Y)}{p(X)} p(Y∣X)=p(X)p(X∣Y)p(Y)
上式称为贝叶斯定理,它提供了从先验概率 p ( Y ) p(Y) p(Y)计算后验概率 p ( Y ∣ X ) p(Y|X) p(Y∣X)的方法。
在分类时,给定测试样本的属性集 X X X,利用训练样本数据可以计算不同类别 Y Y Y值的后验概率,后验概率 p ( Y ∣ X ) p(Y|X) p(Y∣X)最大的类别 Y Y Y可以作为样本的分类。
2.2 朴素贝叶斯分类器
在应用贝叶斯定理时, p ( X ∣ Y ) p(X|Y) p(X∣Y)的计算比较麻烦。但对于属性集 X = X 1 , X 2 , . . . , X n X={X_1,X_2,...,X_n} X=X1,X2,...,Xn,如果 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn之间互相独立,即 p ( X ∣ Y ) = ∏ i = 1 n p ( X i ∣ Y ) p(X|Y)=\prod \limits ^n _{i=1}p(X_i|Y) p(X∣Y)=i=1∏np(Xi∣Y),这个问题就可以由朴素贝叶斯分类器来解决:
p ( Y ∣ X ) = p ( Y ) ∏ i = 1 n p ( X i ∣ Y ) p ( X ) p(Y|X)=\frac {p(Y)\prod \limits ^n _{i=1}p(X_i|Y)}{p(X)} p(Y∣X)=p(X)p(Y)i=1∏np(Xi∣Y)
其中 p ( X ) p(X) p(X)是常数,先验概率 p ( Y ) p(Y) p(Y)可以通过训练集中每类样本所占的比例估计。给定 Y = y Y=y Y=y,如果要估计测试样本 X X X的分类,由朴素贝叶斯分类器得到 y y y类的后验概率:
p ( Y = y ∣ X ) = p ( Y = y ) ∏ i = 1 n p ( X i ∣ Y = y ) p ( X ) p(Y=y|X)=\frac {p(Y=y)\prod \limits ^n _{i=1}p(X_i|Y=y)}{p(X)} p(Y=y∣X)=p(X)p(Y=y)i=1∏np(Xi∣Y=y)
只要找出使 p ( Y = y ) ∏ i = 1 n p ( X i ∣ Y = y ) p(Y=y)\prod \limits ^n _{i=1}p(X_i|Y=y) p(Y=y)i=1∏np(Xi∣Y=y)最大的类别 y y y即可。
朴素贝叶斯分类器简单高效,常用于入侵检测或文本分类等领域。这种分类模型能较好地处理训练样本的噪声和无关属性,减少对数据的过度拟合。
朴素贝叶斯分类器要求严格的条件独立性假设,但现实属性之间一般都有一定的相关性,因此对于实际应用中某些属性有一定相关性的分类问题,效果往往并不理想。
2.2.1 高斯朴素贝叶斯分类器
在估算条件概率 P ( x i ∣ c ) P(x_i|c) P(xi∣c)时,如果 x i x_i xi为连续值,可以使用高斯朴素贝叶斯(Gaussian Naive Bayes)分类模型,它基于一种经典的假设:与每个类相关的连续变量的分布是属于高斯分布的。
2.2.2 多项式朴素贝叶斯分类器
多项式朴素贝叶斯(Multinomial Naive Bayes)经常被用于离散特征的多分类问题,比原始的朴素贝叶斯分类效果有了较大提升。
2.3 朴素贝叶斯分类的主要优点
(1) 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
(2) 对小规模的数据集表现很好,可以处理多分类任务。适合增量式训练,尤其是数据量超出内存时,可以一批批的去增量训练。
(3) 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
2.4 朴素贝叶斯分类的主要缺点
(1) 理论上,朴素贝叶斯模型与其它分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。
(2) 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型原因导致预测效果不佳。
(3) 由于我们是通过先验概率来决定后验概率从而决定分类,所以分类决策存在一定的错误率。
(4) 对输入数据的表达形式很敏感。
3. 贝叶斯分类器在生产中的应用
供电电容是计算机主板生产商必备的工业组件,质量好的供电电容可以提高主板的供电效率,所以供电电容的质量也就直接决定了主板的使用寿命。假设某段时期内某计算机主板制造商所用的供电电容是由三家电容生产商提供的。对制造商在这段时期内的业务数据进行抽样,得到下表所示数据。
| 生产商标识 | 次品率 | 提供电容的份额 |
|---|---|---|
| 1 | 2% | 15% |
| 2 | 1% | 80% |
| 3 | 3% | 5% |
三家电容工厂的供电电容在电脑主板生产商的仓库中是均匀混合的,并无明显的区别标志。现在电脑主板生产商想通过对数据进行分析,解决下面两个问题:
(1) 随机地从仓库中取一只供电电容是次品的概率。
(2)从仓库中随机地取一只供电电容,若已知取到的是一只次品,那么此次品来自哪家工厂的可能性最大。
假设 X X X表示“取到的是一只次品”, Y = i ( i = 1 , 2 , 3 ) Y=i(i=1,2,3) Y=i(i=1,2,3)表示“取到的产品是由第 i i i家工厂提供的”,则问题转化为求解 p ( X ) p(X) p(X)与 p ( Y = i ∣ X ) p(Y=i|X) p(Y=i∣X)。由上表得到后验概率为:
p ( X ∣ Y = 1 ) = 2 % , p ( X ∣ Y = 2 ) = 1 % , p ( X ∣ Y = 3 ) = 3 % p(X|Y=1)=2 \%, p(X|Y=2)=1 \%, p(X|Y=3)=3 \% p(X∣Y=1)=2%,p(X∣Y=2)=1%,p(X∣Y=3)=3%
先验概率为:
p ( Y = 1 ) = 15 % , p ( Y = 2 ) = 80 % , p ( Y = 3 ) = 5 % p(Y=1)=15 \%, p(Y=2)=80 \%, p(Y=3)=5 \% p(Y=1)=15%,p(Y=2)=80%,p(Y=3)=5%
由全概率公式计算得出:
p ( X ) = p ( X ∣ Y = 1 ) p ( Y = 1 ) + p ( X ∣ Y = 2 ) p ( Y = 2 ) + p ( X ∣ Y = 3 ) p ( Y = 3 ) = 0.02 ∗ 0.15 + 0.01 ∗ 0.8 + 0.03 ∗ 0.05 = 0.0125 p(X) = p(X|Y=1)p(Y=1)+p(X|Y=2)p(Y=2)+p(X|Y=3)p(Y=3) \\ =0.02*0.15+0.01*0.8+0.03*0.05=0.0125 p(X)=p(X∣Y=1)p(Y=1)+p(X∣Y=2)p(Y=2)+p(X∣Y=3)p(Y=3)=0.02∗0.15+0.01∗0.8+0.03∗0.05=0.0125
然后求解 p ( Y = i ∣ X ) p(Y=i|X) p(Y=i∣X),根据贝叶斯定理可得:
p ( Y = i ∣ X ) = p ( X ∣ Y = i ) p ( Y = i ) p ( X ) p(Y=i|X)=\frac {p(X|Y=i)p(Y=i)}{p(X)} p(Y=i∣X)=p(X)p(X∣Y=i)p(Y=i)
由上式可以计算次品出自厂商1的概率为:
p ( Y = 1 ∣ X ) = p ( X ∣ Y = 1 ) p ( Y = 1 ) p ( X ) = 0.02 ∗ 0.15 0.0125 = 0.24 p(Y=1|X)=\frac {p(X|Y=1)p(Y=1)}{p(X)}=\frac{0.02*0.15}{0.0125}=0.24 p(Y=1∣X)=p(X)p(X∣Y=1)p(Y=1)=0.01250.02∗0.15=0.24
类似地可以计算次品出自其他两个厂商的概率为:
p ( Y = 2 ∣ X ) = 0.64 , p ( Y = 3 ∣ X ) = 0.12 p(Y=2|X)=0.64,p(Y=3|X)=0.12 p(Y=2∣X)=0.64,p(Y=3∣X)=0.12
可见,从仓库中随机地取一只电容,如果是一只次品,那么此次品来自工厂2的可能性最大。
4. 朴素贝叶斯分类器的Python实现
利用scikit-learn中朴素贝叶斯的分类算法
from sklearn.datasets import load_iris
from sklearn.naive_bayes import GaussianNB
iris = load_iris()
clf = GaussianNB()# 设置高斯贝叶斯分类器
clf.fit(iris.data,iris.target)# 训练分类器
y_pred = clf.predict(iris.data)# 预测
print("Number of mislabeled points out of %d points:%d" %(iris.data.shape[0],(iris.target!= y_pred).sum()))
Number of mislabeled points out of 150 points:6
from sklearn.datasets import load_iris
from sklearn.naive_bayes import MultinomialNB
iris = load_iris()
gnb =MultinomialNB()# 设置多项式贝叶斯分类器
gnb.fit(iris.data,iris.target)
y_pred=gnb.predict(iris.data)
print('Number of mislabeled points out of a total %d points: %d' %(iris.data.shape[0],(iris.target!= y_pred).sum()))
Number of mislabeled points out of a total 150 points: 7
5. 贝叶斯分类器和Logistic回归分类边界的对比
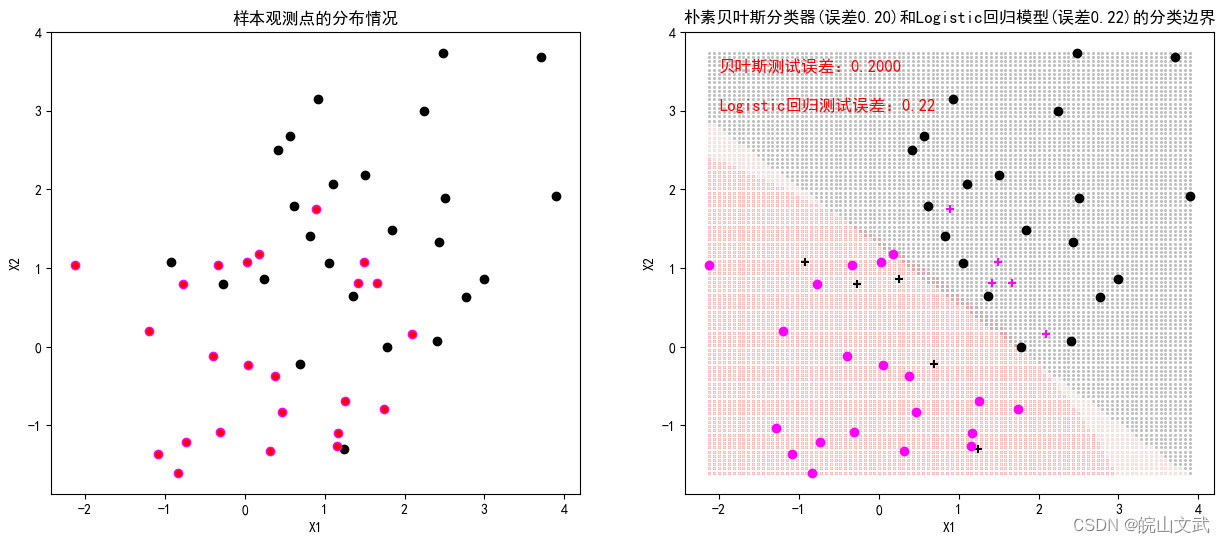
基于模拟数据分别建立朴素贝叶斯分类器和Logistic回归模型,并绘制两个分类模型的分类边界,展示两者的特点和区别。
代码及运行结果如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文显示乱码问题
plt.rcParams['axes.unicode_minus']=False
import warnings
warnings.filterwarnings(action = 'ignore')
from scipy.stats import beta
from sklearn.naive_bayes import GaussianNB
import sklearn.linear_model as LM
from sklearn.model_selection import cross_val_score,cross_validate,train_test_split
from sklearn.metrics import classification_report
from sklearn.metrics import roc_curve, auc,accuracy_score,precision_recall_curve
np.random.seed(123)
N=50
n=int(0.5*N)
X=np.random.normal(0,1,size=100).reshape(N,2)
Y=[0]*n+[1]*n
X[0:n]=X[0:n]+1.5fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(15,6))
axes[0].scatter(X[:n,0],X[:n,1],color='black',marker='o')
axes[0].scatter(X[(n+1):N,0],X[(n+1):N,1],edgecolors='magenta',marker='o',c='r')
axes[0].set_title("样本观测点的分布情况")
axes[0].set_xlabel("X1")
axes[0].set_ylabel("X2")modelNB = GaussianNB()
modelNB.fit(X, Y)
modelLR=LM.LogisticRegression()
modelLR.fit(X,Y)
Data=np.hstack((X,np.array(Y).reshape(N,1)))
Yhat=modelNB.predict(X)
Data=np.hstack((Data,Yhat.reshape(N,1)))
Data=pd.DataFrame(Data)X1,X2 = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),100), np.linspace(X[:,1].min(),X[:,1].max(),100))
New=np.hstack((X1.reshape(10000,1),X2.reshape(10000,1)))
YnewHat1=modelNB.predict(New)
DataNew=np.hstack((New,YnewHat1.reshape(10000,1)))
YnewHat2=modelLR.predict(New)
DataNew=np.hstack((DataNew,YnewHat2.reshape(10000,1)))
DataNew=pd.DataFrame(DataNew)for k,c in [(0,'silver'),(1,'red')]:axes[1].scatter(DataNew.loc[DataNew[2]==k,0],DataNew.loc[DataNew[2]==k,1],color=c,marker='o',s=1)
for k,c in [(0,'silver'),(1,'mistyrose')]:axes[1].scatter(DataNew.loc[DataNew[3]==k,0],DataNew.loc[DataNew[3]==k,1],color=c,marker='o',s=1)axes[1].scatter(X[:n,0],X[:n,1],color='black',marker='+')
axes[1].scatter(X[(n+1):N,0],X[(n+1):N,1],color='magenta',marker='+')
for k,c in [(0,'black'),(1,'magenta')]:axes[1].scatter(Data.loc[(Data[2]==k) & (Data[3]==k),0],Data.loc[(Data[2]==k) & (Data[3]==k),1],color=c,marker='o')
axes[1].set_title("朴素贝叶斯分类器(误差%.2f)和Logistic回归模型(误差%.2f)的分类边界"%(1-modelNB.score(X,Y),1-modelLR.score(X,Y)))
axes[1].set_xlabel("X1")
axes[1].set_ylabel("X2")np.random.seed(123)
k=10
CVscore=cross_validate(modelNB,X,Y,cv=k,scoring='accuracy',return_train_score=True)
axes[1].text(-2,3.5,'贝叶斯测试误差:%.4f' %(1-CVscore['test_score'].mean()),fontsize=12,color='r')
CVscore=cross_validate(modelLR,X,Y,cv=k,scoring='accuracy',return_train_score=True)
axes[1].text(-2,3,"Logistic回归测试误差:%.2f" %(1-CVscore['test_score'].mean()),fontsize=12,color='r')
plt.show()
6. 空气污染的分类预测
基于空气质量监测数据,采用朴素贝叶斯分类器对是否出现空气污染进行二分类预测,然后采用各种方式对预测模型进行评价。
代码及运行结果如下:
data=pd.read_excel('北京市空气质量数据.xlsx')
data=data.replace(0,np.NaN)
data=data.dropna()
data['有无污染']=data['质量等级'].map({'优':0,'良':0,'轻度污染':1,'中度污染':1,'重度污染':1,'严重污染':1})
data['有无污染'].value_counts()
X=data.loc[:,['PM2.5','PM10','SO2','CO','NO2','O3']]
Y=data.loc[:,'有无污染']modelNB = GaussianNB()
modelNB.fit(X, Y)
modelLR=LM.LogisticRegression()
modelLR.fit(X,Y)
print('评价模型结果:\n',classification_report(Y,modelNB.predict(X)))评价模型结果:precision recall f1-score support0 0.86 0.94 0.90 12041 0.90 0.79 0.84 892accuracy 0.88 2096macro avg 0.88 0.87 0.87 2096
weighted avg 0.88 0.88 0.87 2096
接下来,利用ROC和P-R曲线对比朴素贝叶斯分类器和Logistic回归模型的预测性能。
代码及运行结果如下:
fig,axes=plt.subplots(nrows=1,ncols=2,figsize=(10,4))
fpr,tpr,thresholds = roc_curve(Y,modelNB.predict_proba(X)[:,1],pos_label=1)
fpr1,tpr1,thresholds1 = roc_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1)
axes[0].plot(fpr, tpr, color='r',label='贝叶斯ROC(AUC = %0.5f)' % auc(fpr,tpr))
axes[0].plot(fpr1, tpr1, color='blue',linestyle='-.',label='Logistic回归ROC(AUC = %0.5f)' % auc(fpr1,tpr1))
axes[0].plot([0, 1], [0, 1], color='navy', linewidth=2, linestyle='--')
axes[0].set_xlim([-0.01, 1.01])
axes[0].set_ylim([-0.01, 1.01])
axes[0].set_xlabel('FPR')
axes[0].set_ylabel('TPR')
axes[0].set_title('两个分类模型的ROC曲线')
axes[0].legend(loc="lower right")pre, rec, thresholds = precision_recall_curve(Y,modelNB.predict_proba(X)[:,1],pos_label=1)
pre1, rec1, thresholds1 = precision_recall_curve(Y,modelLR.predict_proba(X)[:,1],pos_label=1)
axes[1].plot(rec, pre, color='r',label='贝叶斯总正确率 = %0.3f)' % accuracy_score(Y,modelNB.predict(X)))
axes[1].plot(rec1, pre1, color='blue',linestyle='-.',label='Logistic回归总正确率 = %0.3f)' % accuracy_score(Y,modelLR.predict(X)))
axes[1].plot([0,1],[1,pre.min()],color='navy', linewidth=2, linestyle='--')
axes[1].set_xlim([-0.01, 1.01])
axes[1].set_ylim([pre.min()-0.01, 1.01])
axes[1].set_xlabel('查全率R')
axes[1].set_ylabel('查准率P')
axes[1].set_title('两个分类模型的P-R曲线')
axes[1].legend(loc='lower left')
plt.show()
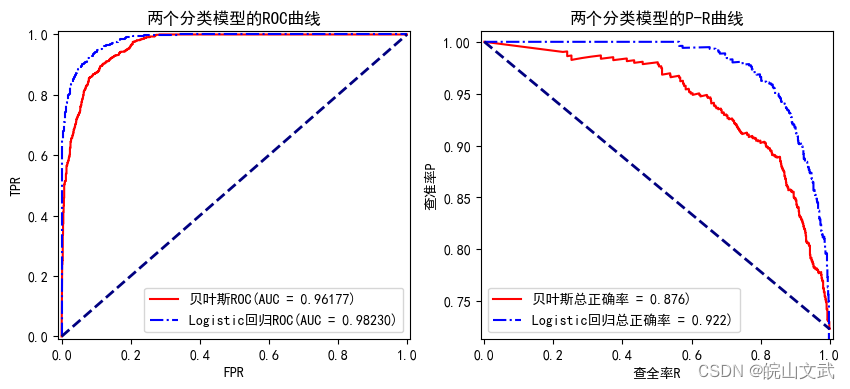
图中,两个回归模型的ROC曲线均远离基准线,且曲线下的面积分别约等于0.96和0.98,表明朴素贝叶斯模型虽然较好地实现二分类预测,但整体性能略低于Logistic回归模型。在P-R曲线中,随着查全率R的增加,Logistic回归模型的查准率P并没有快速下降,优于朴素贝叶斯分类器,且正确率较高。故对于该问题Logistic回归模型表现更好。
相关文章:

数据挖掘|贝叶斯分类器及其Python实现
分类分析|贝叶斯分类器及其Python实现 0. 分类分析概述1. Logistics回归模型2. 贝叶斯分类器2.1 贝叶斯定理2.2 朴素贝叶斯分类器2.2.1 高斯朴素贝叶斯分类器2.2.2 多项式朴素贝叶斯分类器 2.3 朴素贝叶斯分类的主要优点2.4 朴素贝叶斯分类的主要缺点 3. 贝叶斯分类器在生产中的…...
Linux文件(系统)IO(含动静态库的链接操作)
文章目录 Linux文件(系统)IO(含动静态库的链接操作)1、C语言文件IO操作2、三个数据流stdin、stdout、stderr3、系统文件IO3.1、相关系统调用接口的使用3.2、文件描述符fd3.3、文件描述符的分配规则3.3、重定向3.4、自制shell加入重…...
CI/CD实战-jenkins结合ansible 7
配置主机环境 在jenkins上断开并删除docker1节点 重新给master添加构建任务 将server3,server4作为测试主机,停掉其上后面的docker 在server2(jenkins)主机上安装ansible 设置jenkins用户到目标主机的免密 给测试主机创建用户并…...
内网渗透-(黄金票据和白银票据)详解(一)
目录 一、Kerberos协议 二、下面我们来具体分析Kerberos认证流程的每个步骤: 1、KRB_AS-REQ请求包分析 PA-ENC-TIMESTAMP PA_PAC_REQUEST 2、 KRB_AS_REP回复包分析: TGT认购权证 Logon Session Key ticket 3、然后继续来讲相关的TGS的认证过程…...
学习transformer模型-Dropout的简明介绍
Dropout的定义和目的: Dropout 是一种神经网络正则化技术,它在训练时以指定的概率丢弃一个单元(以及连接)p。 这个想法是为了防止神经网络变得过于依赖特定连接的共同适应,因为这可能是过度拟合的症状。直观上&#…...
游戏引擎中的大气和云的渲染
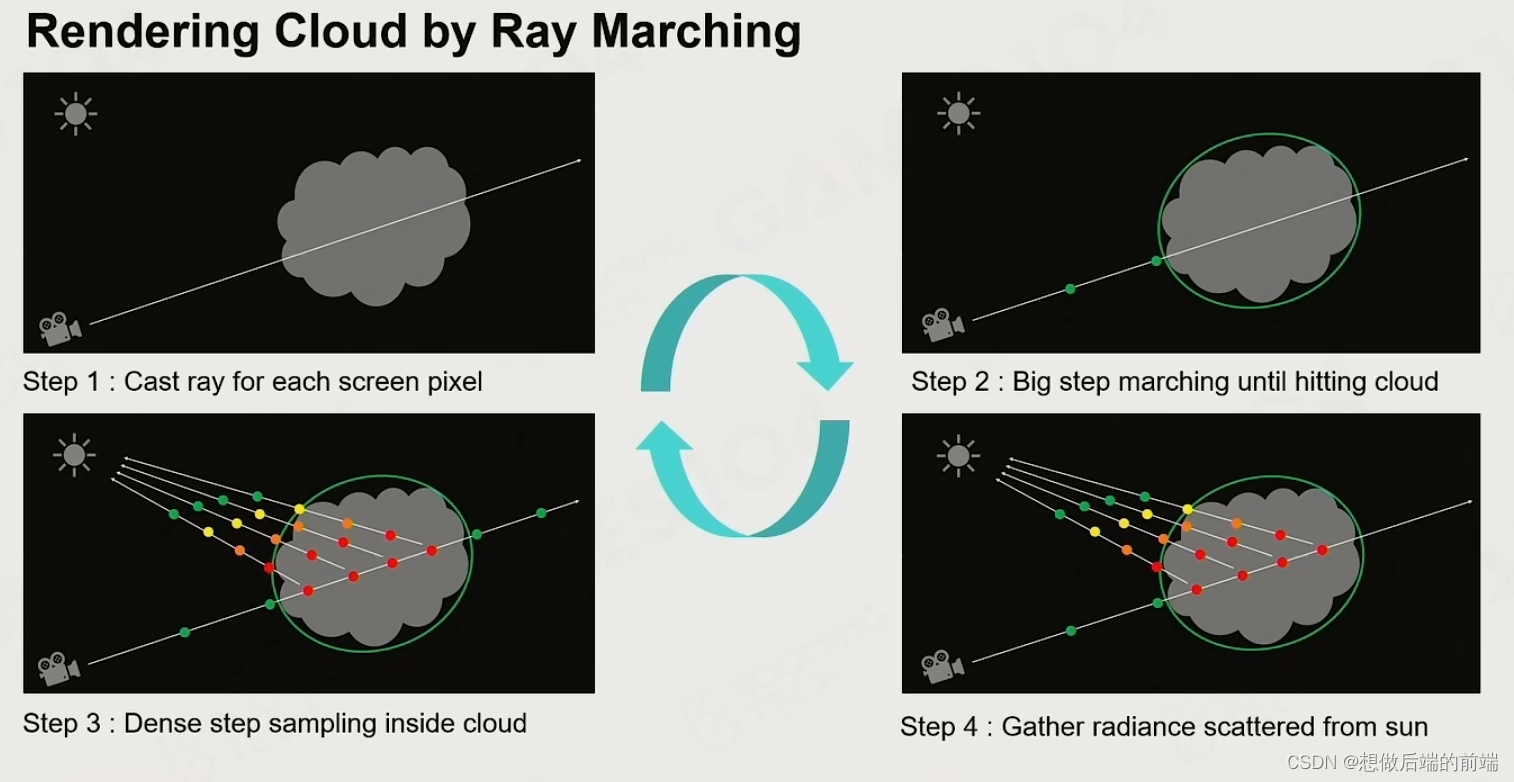
一、大气 首先和光线追踪类似,大气渲染也有类似的渲染公式,在实际处理中也有类似 Blinn-Phong的拟合模型。关键参数是当前点到天顶的角度和到太阳的角度 二、大气散射理论 光和介质的接触: Absorption 吸收Out-scattering 散射Emission …...

华为鲲鹏云认证考试内容有哪些?华为鲲鹏云认证考试报名条件
华为鲲鹏云认证考试是华为公司为了验证IT专业人士在鲲鹏计算及云计算领域的专业能力而设立的一项认证考试。以下是关于华为鲲鹏云认证考试的一些详细信息: 考试内容:华为鲲鹏云认证考试的内容主要包括理论考核和实践考核两大部分。理论考核涉及云计算、…...
v3-admin-vite 改造自动路由,view页面自解释Meta
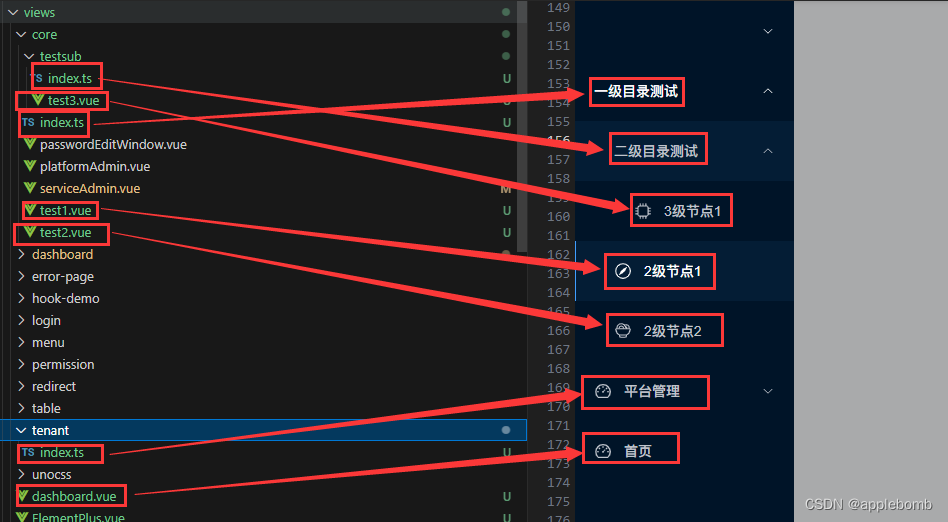
需求 v3-admin-vite是一款不错的后端管理模板,主要是pany一直都在维护,最近将后台管理也进行了升级,顺便完成一直没时间解决的小痛痒: 在不使用后端动态管理的情况下。我不希望单独维护一份路由定义,我希望页面是自解…...

FIFO存储器选型参数,结构原理,工艺与注意问题总结
🏡《总目录》 目录 1,概述2.1,写入操作2.2,读取操作2.3,指针移动与循环2.4,状态检测3,结构特点3.1,双口RAM结构3.2,无外部读写地址线3.3,内部读写指针自动递增3.4,固定深度的缓冲区4,工艺流程4.1,硅晶圆准备...

jvm高级面试题-2024
说下对JVM内存模型的理解 JVM内存模型主要是指Java虚拟机在运行时所使用的内存结构。它主要包括堆、栈、方法区和程序计数器等部分。 堆是JVM中最大的一块内存区域,用于存储对象实例。一般通过new关键字创建的对象都存放在堆中,堆的大小可以通过启动参数…...

DeepL Pro3.1 下载地址及安装教程
DeepL Pro是DeepL公司推出的专业翻译服务。DeepL是一家专注于机器翻译和自然语言处理技术的公司,其翻译引擎被认为在质量和准确性方面表现优秀.DeepL Pro提供了一系列高级功能和服务,以满足专业用户的翻译需求。其中包括: 高质量翻译…...

第十一届 “MathorCup“- B题:基于机器学习的团簇能量预测及结构全局寻优方法
目录 摘 要 第 1 章 问题重述 1.1 问题背景 1.2 问题描述 第 2 章 思路分析...
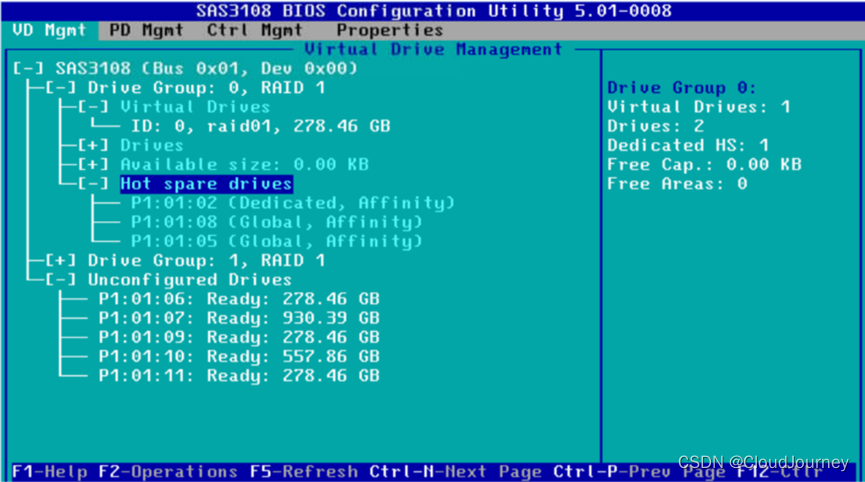
云计算探索-如何在服务器上配置RAID(附模拟器)
一,引言 RAID(Redundant Array of Independent Disks)是一种将多个物理硬盘组合成一个逻辑单元的技术,旨在提升数据存取速度、增大存储容量以及提高数据可靠性。在服务器环境中配置RAID尤其重要,它不仅能够应对高并发访…...
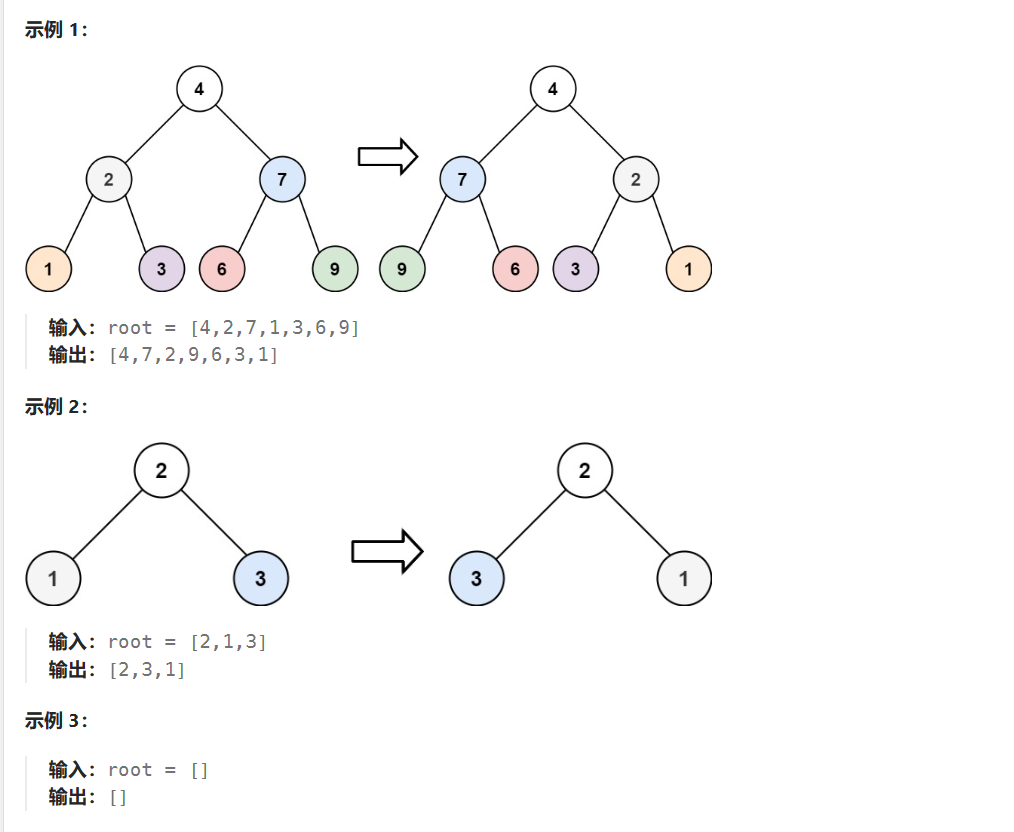
LeetCode226:反转二叉树
题目描述 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 解题思想 使用前序遍历和后序遍历比较方便 代码 class Solution { public:TreeNode* invertTree(TreeNode* root) {if (root nullptr) return root;swap(root->left, root…...

特征融合篇 | 利用RT-DETR的AIFI去替换YOLOv8中的SPPF(附2种改进方法)
前言:Hello大家好,我是小哥谈。RT-DETR模型是一种用于目标检测的深度学习模型,它基于transformer架构,特别适用于实时处理序列数据。在RT-DETR模型中,AIFI(基于注意力的内部尺度特征交互)模块是一个关键组件,它通过引入注意力机制来增强模型对局部和全局信息的处理能力…...
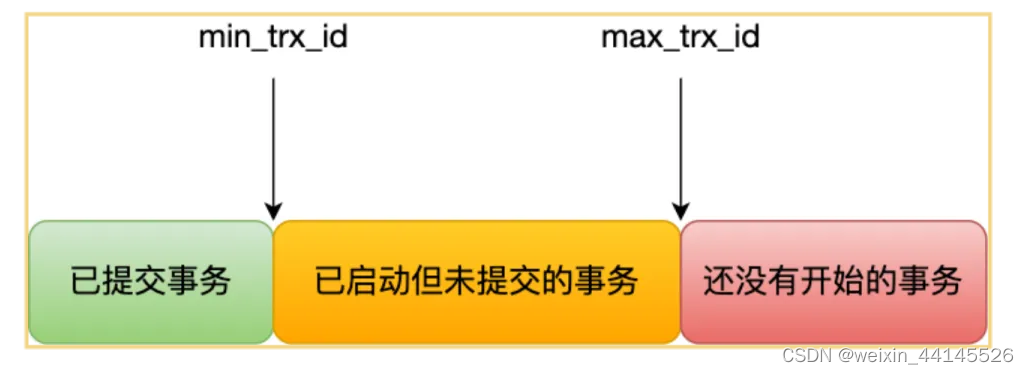
MVCC多版本并发控制
1.什么是MVCC MVCC (Multiversion Concurrency Control),多版本并发控制。MySQL通过MVCC来实现隔离性。隔离性本质上是因为同时存在多个并发事务可能会导致脏读、幻读等情况。要解决并发问题只有一种方案就是加锁。当然,锁不可避免…...

图片转换成base64如何在html文件中使用呢
在HTML文件中使用Base64编码的图片非常简单。Base64编码是一种将二进制数据转换为ASCII字符串的方法,这使得可以直接在网页上嵌入图片数据,而无需引用外部图片文件。以下是如何在HTML中使用Base64编码的图片的步骤: 步骤 1: 将图片转换为Bas…...
【MATLAB源码-第24期】基于matlab的水声通信中海洋噪声的建模仿真,对比不同风速的影响。
操作环境: MATLAB 2022a 1、算法描述 水声通信: 水声通信是一种利用水中传播声波的方式进行信息传递的技术。它在水下环境中被广泛应用,特别是在海洋科学研究、海洋资源勘探、水下军事通信等领域。 1. **传输媒介**:水声通信利…...

七、函数的使用方法
函数的调用 nameinput()#输入参数并赋值name print(name)#d打印name 格式:返回值函数名(参数) def get_sum(n):#形式参数计算累加和:param n::return: sumsum0for i in range(1,n1):sumiprint…...

数据分析之Tebleau 简介、安装及数据导入
Tebleau简介 Tebleau基于斯坦福大学突破性交互式技术 可以将结构化数据快速生成图表、坐标图、仪表盘与报告 将维度拖放到画布等地方是他的主要操作方式 例:Tebleau是手机相机 (相对来说更简单) POWER BI是单反相机 Tebleau各类产品 Teblea…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...

Ray框架:分布式AI训练与调参实践
Ray框架:分布式AI训练与调参实践 系统化学习人工智能网站(收藏):https://www.captainbed.cn/flu 文章目录 Ray框架:分布式AI训练与调参实践摘要引言框架架构解析1. 核心组件设计2. 关键技术实现2.1 动态资源调度2.2 …...

[10-1]I2C通信协议 江协科技学习笔记(17个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17...
