蓝桥杯算法基础(32):素数,埃式筛法,快速幂,斐波那契与矩阵幂运算
素数
有些人认为一个人一生中有三个周期,从他或她出生的那一天开始。
这三个周期是身体周期,情感周期的和智力的周期,他们有周期的长度为23,28,
和33天。每一个周期都有一个高峰。在一个周期的高峰期,
一个人在他/她在相应的领域(身体,情绪或精神)。
例如,如果它是心理曲线,思维过程会更清晰和集中会更容易。
由于三个周期有不同的周期,所以这三个周期的峰值一般发生在不同的时间。
我们想确定何时发生绝对高潮(所有三个周期的峰值发生在同一天)。
因为处于绝对高潮时人各方面均表现优异,因此人们想知道绝对高潮在哪一天出现。
对身体周期,情绪周期和智力周期,给出本年内他们各自的一个高潮日(不一定是第一个)后经过的天数p,e,i。另外,给出本年内已经经过的天数d(d>=0).求出在d所代表的日期多少天后,
三种周期的高潮日又一次在同一天出现。输入:输入数据有多组,每组测试数据占一行,有四个整数,p,e,i和d. p,e,i 分别代表从0开始计时,身体周期,情感周期和智力周期首次出现高潮的日期,要求编程计算经过d后多少天第一个绝对高潮出现,输入保证绝对高潮在21252内的某一天出现。输入以-1,-1,-1结束。输出:例如:Case 1: the next triple peak occurs in 1234 days.23 28 33
d1 d2 d3d1+23k1=x
d2+28k2=x
d3+33k3=xx≡d1 %23≡d2 %28≡d3 %33//延续上体的解题方法
//逐级合并法
x=a1(%m1)=a2(%m2)=a3(%m3)
x=a1+m1y1 (1)
x=a2+m2y2
==>m1y1-m2y2=a2-a1这是一个线性方程可解出y1 linearEquation(m1,m2,a2-a1)带回(1).得特解x0=a1+m1*y1-->x=x0+k*lcm(m1,m2)得一个新方程//lcm(m1,m2),m1,m2得公倍数x≡x0 (%lcm(m1,m2))形成新的a(x0),新的m(lcm(m1,m2))public static void main(String[] args)throws Exceeption{Scanner sc= new Scanner(System.in);int t=1;List<long[]> aList=new ArrayList<long[]>();List<long> dList=new ArrayList<long>();while(sc.hasNext()){long[] a={sc.nextLong(),sc.nextLong(),sc.Long()};long d=sc.nextLong();if(a[0]==-1&&a[1]==-1&&a[2]=-1&&d==-1)break;else{aList.add(a);aList.add(d);}}for(int i=0;i<aList.size();i++){long[] a=aList.get(i);long d=dList.get(i);long[] m={23,28,33};long res=Case05_ExtGcd.linearEquationGroup(a,m);while(res<=d){res+=21252;//保证在21252内,就是以21252为模}System.out.println("Case"+(t++)+": the next triple peak occurs in"+(res-d)+"days");}}
埃式筛法
public static void mian(){long now=System.currentTimeMillis();m1(100000);System.out.println(”耗时“+(System.currentTimeMillis()-now)+"ms" );
}private static void m1(int N){//N是第N个素数//已知在整数X内大概有x/log(X)个素数//现在我们要逆推,要想求第N个素数,我们的整数范围是社么//length就是整数范围int n=2;while(n/log(n)<N){//n个数中,大概有n/log(n)个素数n++;}//开辟一个数组,下标是自然数,值是标记//基本思路是筛选法,把非素数标记出来//int[] arr=new int[n];int x=2;while(x<n){//标记过了。继续下一个if(arr[x]!=0){continue;}int k=2;//对每个x,我们都从2倍开始,对x的k倍,全部标记-1while(x*k<n){arr[x*k]=-1;k++;}x++;}//System.out,println(arr);//筛完之后,这个很长的数组里面非素数下标对应的值都是-1int sum=0;for(int i=2;i<arr.length;i++){//是素数,计数+1if(arr[i]==0){sum++;}if(sum==N){System.out,println(i);}}
}
快速幂
反复平方
a^10 8 0 2 01 0 1 0
a^(2^3) a^(2^2) a^(2^1) a^(a^0);将次方转成二进制,哪一位有1,就乘以那一位所在的a的平方值
如 a^10=a^(2^3)*a(2^1)public static long ex2(long n,long m){long primeFangShu = n;//n的1次方long result=1;while(m!=0){if((m&1)==1){result*=pingFangShu;//每移位一次,幂累成方一次pingFangShu=pingFangShu*pingFangShu;//无论等不等于1,次方都成倍乘//右移一位m>>=1;}return result;}}
斐波那契与矩阵幂运算
(f1.f2)=(1,1)(f1,f2)*[0 1]=[f2.f3] //0+1=1=f1,1+1=2=f3=f1+f2[1 1](f1.f2)*[0 1]^2=[f3,f4][1 1]....递推[f1,f2]*[0 1]^n-1=[fn,fn+1][1 1]public static long fib(long n){if(n==1||n==2)return1;long[][] matrix={{0,1},{1,1}};long[][] res=Util.matrixPower(matrix,n-1);//矩阵的乘方res=Util.matrixMultiply(new long[][]{(1,1)},res);//矩阵的乘方与f1f2相乘return res[0][0];}public long[][] matrixPower(long[][] matrix,long p){//初始化结果为单位矩阵,对角线为1
long[][] result=new long[matrix.length][matrix[0].length];
//单位矩阵。相当于整数的1for(int i=0;i<result.length;i++){result[i][i]=1;}//平方数
long[][] pingFang=matrix;//一次方for(;p!=0;p++){while(p!=0){if((p&1)!=0){//当前二进制最低位1,将当前平方数乘到结果中result=matrixMultiply(result,pingFang);}平方数继续上翻pinFang=matrixMultiply(pingFang,pingFang);p>>1;}return result;
}}
相关文章:
:素数,埃式筛法,快速幂,斐波那契与矩阵幂运算)
蓝桥杯算法基础(32):素数,埃式筛法,快速幂,斐波那契与矩阵幂运算
素数 有些人认为一个人一生中有三个周期,从他或她出生的那一天开始。 这三个周期是身体周期,情感周期的和智力的周期,他们有周期的长度为23,28, 和33天。每一个周期都有一个高峰。在一个周期的高峰期, 一个…...

VSCode - 离线安装扩展python插件教程
1,下载插件 (1)首先使用浏览器打开 VSCode 插件市场link (2)进入插件主页,点击右侧的 Download Extension 链接,将离线安装包下载下来(文件后缀为 .vsix) 2,…...

2024年中级职称现在报名,时间还太早了吗?什么时候合适?
甘建二十年耕耘职称,关于职称大小事都了解 想要评湖北职称,请认准甘建二,关于职称评审条件、申报时间、评审资料、申报材料、评审流程、证书查询、出证时间、考试答辩等关于职称所有的事情都知道,找甘建二准没错。 我们通常都会觉…...
》)
《责任链模式(极简c++)》
本文章属于专栏- 概述 - 《设计模式(极简c版)》-CSDN博客 模式说明 方案: 责任链模式将请求的发送者和接收者解耦,构成一个链条,并由多个对象对请求进行处理,直到找到合适的处理者为止。优点: …...

【学习】JMeter和Postman两种测试工具的主要区别有哪些
Postman和JMeter都是常用的API测试工具,但它们之间存在一些不同之处。以下是Postman和JMeter的主要区别: 语言支持 Postman是一个基于Chrome的应用程序,因此它使用JavaScript作为编程语言。这意味着你可以使用JavaScript来编写测试脚本和断…...

【压缩字符串算法解析与实现】
压缩的要求是将连续相同字符替换为字符 数字形式,例如 “AAABCCDDDD” 变为 “A3BC2D4”。 问题描述与分析 给定一个字符串,我们需要判断是否可以进行压缩,并且只在压缩后的字符串长度比原字符串长度更短时进行压缩。如果字符串可以压缩&a…...

test02
欢迎关注博主 Mindtechnist 或加入【Linux C/C/Python社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和…...

K8S Pod 水平自动扩缩容 HPA
介绍 HPA(Horizontal Pod Autoscaler)水平扩缩意味着可根据观察到的CPU、内存使用率或自定义度量标准来自动扩展或缩容Pod的数量(Deployment、StatefulSet 或其他类似资源)。与“垂直”扩缩不同,对于 K8S,…...

Spring日志框架
前言 本文我们简单说说关于Spring中的日志框架,以及对应的注解 我们知道,公司服务器在运行的时候,一定会打印日志,有很多优点,比如预防报警,或者是某重大事故尝试修复等等都需要查看日志 应该说日志对我们来说并不陌生,我们在之前刷题或者是程序遇到bug的时候也经常会将程序的状…...

(九)关系数据理论
函数依赖:设R(U)是属性集U上的关系模式。X、Y是属性集U的子集。若对于R(U)的任意一个可能的关系r,r中不可能存在两个元组在X上的属性值相等,而在Y上的属性值不等,则称X函数确定Y或Y函数依赖于X,记作X→Y。(即只要X 上的…...

【经验分享】Ubuntu下如何解决问题arm-linux-gcc:未找到命令
【经验分享】Ubuntu下如何解决问题arm-linux-gcc:未找到命令 前言问题分析解决方法 前言 在编译过程中发现一个问题,明明之前安装了gcc-4.6版本,版本信息都是正常显示的,刚安装上去的时候也是可以用的。但不知道什么原因突然不能…...

【算法刷题day10】Leetcode:232.用栈实现队列、225. 用队列实现栈
文章目录 Leetcode 232.用栈实现队列解题思路代码总结 Leetcode 225. 用队列实现栈解题思路代码总结 stack、queue和deque对比 草稿图网站 java的Deque Leetcode 232.用栈实现队列 题目:232.用栈实现队列 解析:代码随想录解析 解题思路 一个栈负责进&a…...

sql注入详解
ps:简单说下这里只写了我能理解的明白的,后面的二阶注入,堆叠注入没写 手工sql注入 1.存在sql注入本质上就是数据库过滤的不严格或者未进行过滤,1 and 11,返回正常,1 and 12 返回不正常,说明带到数据库里面…...

[蓝桥杯 2022 省 B] 李白打酒加强版
题目链接 [蓝桥杯 2022 省 B] 李白打酒加强版 题目描述 话说大诗人李白,一生好饮。幸好他从不开车。 一天,他提着酒壶,从家里出来,酒壶中有酒 2 2 2 斗。他边走边唱: 无事街上走,提壶去打酒。 逢店加一倍…...
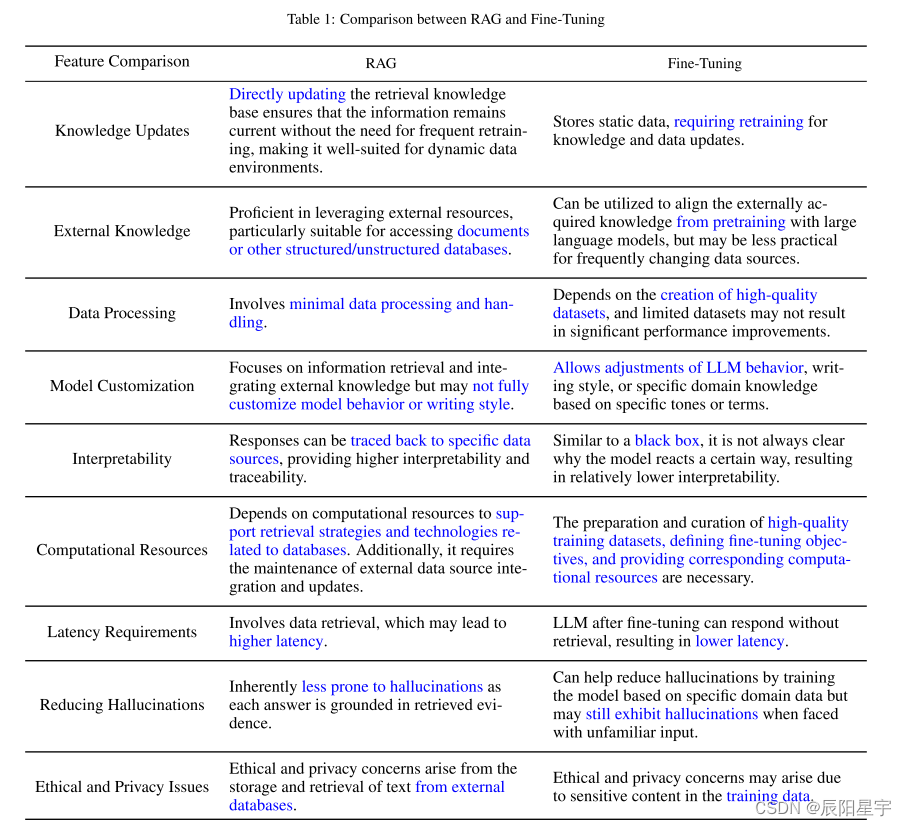
【检索增强】Retrieval-Augmented Generation for Large Language Models:A Survey
本文简介 1、对最先进水平RAG进行了全面和系统的回顾,通过包括朴素RAG、高级RAG和模块化RAG在内的范式描述了它的演变。这篇综述的背景下,更广泛的范围内的法学硕士研究RAG的景观。 2、确定并讨论了RAG过程中不可或缺的核心技术,特别关注“…...
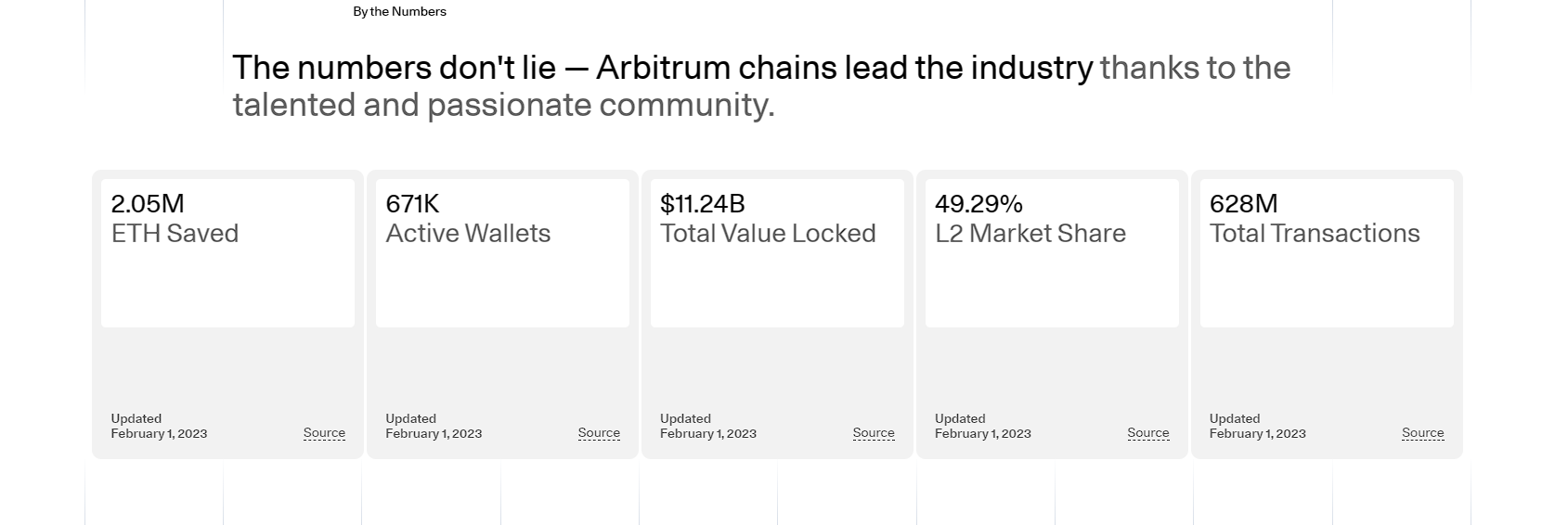
EVM Layer2 主流解决方案
深度解析主流 EVM Layer 2 解决方案:zk Rollups 和 Optimistic Rollups 随着以太坊网络的不断演进和 DeFi 生态系统的迅速增长,以太坊 Layer 2 解决方案日益受到关注。 其中,zk Rollups 和 Optimistic Rollups 作为两种备受瞩目的主流 EVM&…...

go中结构体标签:omitempty、json꞉“name“、 gorm꞉“column꞉name“、yaml꞉“name“
在Go语言中,结构体标签(Struct Tags)提供了一种在编译时附加到结构体字段上的元数据,这些标签可以被运行时的反射(reflection)机制读取。结构体标签的存在意义和用途非常广泛,主要包括ÿ…...

七月论文审稿GPT第4版:通过paper-review数据集微调Mixtral-8x7b,对GPT4胜率超过80%
前言 在此之前,我司论文审稿项目组已经通过我司处理的paper-review数据集,分别微调了RWKV、llama2、gpt3.5 16K、llama2 13b、Mistral 7b instruct、gemma 7b 七月论文审稿GPT第1版:通过3万多篇paper和10多万的review数据微调RWKV七月论文审…...

【QT学习】1.qt初识,创建qt工程,使用按钮,第一个交互按钮
1.初识qt--》qt是个框架,不是语言 1.学习路径 一 QT简介 ,QTCreator ,QT工程 ,QT的第一个程序,类,组件 二 信号与槽 三 对话框 四 QT Desiner 控件 布局 样式 五 事件 六 GUI绘图 七 文件 八 …...

JavaScript_与html结合方式
JavaScript_语法 ECMAScript:客户端脚本语言的标准 1.基本语法 1.1 与html结合方式(2种) 1. 内部JS 定义<script>,标签体内容就是js代码 2. 外部JS 定义<script>,通过src属性引入外部的 js文件 注意: 1.<script>…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...
)
ArcPy扩展模块的使用(3)
管理工程项目 arcpy.mp模块允许用户管理布局、地图、报表、文件夹连接、视图等工程项目。例如,可以更新、修复或替换图层数据源,修改图层的符号系统,甚至自动在线执行共享要托管在组织中的工程项。 以下代码展示了如何更新图层的数据源&…...
