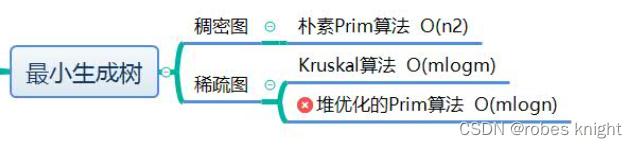
图论- 最小生成树
一、最小生成树-prim算法
1.1 最小生成树概念
一幅图可以有很多不同的生成树,比如下面这幅图,红色的边就组成了两棵不同的生成树:
对于加权图,每条边都有权重(用最小生成树算法的现实场景中,图的边权重一般代表成本、距离这样的标量),所以每棵生成树都有一个权重和。比如上图,右侧生成树的权重和显然比左侧生成树的权重和要小。
那么最小生成树很好理解了,所有可能的生成树(包含所有顶点)中,权重和最小的那棵生成树就叫「最小生成树」。
1.2 稠密图-朴素prim
和djikstra很像
const int INF = 0x3f3f3f3f; // 定义一个非常大的数,用作无穷远的初始化值
int n; // n表示图中的顶点数
int g[N][N]; // 邻接矩阵,用于存储图中所有边的权重
int dist[N]; // 用于存储其他顶点到当前最小生成树的最小距离
bool st[N]; // 用于标记每个顶点是否已经被加入到最小生成树中// Prim算法的实现,返回最小生成树的总权重
int prim() {memset(dist, 0x3f, sizeof dist); // 初始化所有顶点到MST的距离为无穷远int res = 0; // 存储最小生成树的总权重for (int i = 0; i < n; i++) { // 主循环,每次添加一个顶点到MSTint t = -1; // 用于找到当前未加入MST且dist最小的顶点for (int j = 1; j <= n; j++) // 遍历所有顶点,找到tif (!st[j] && (t == -1 || dist[t] > dist[j]))t = j;//t就是当前加入最小生成树的顶点if (i && dist[t] == INF) return INF; // 如果图不连通,则返回INFif (i) res += dist[t]; // 非首次迭代时,累加到MST的距离st[t] = true; // 将顶点t加入到MST中//再从T出发,更新所有未加入顶点到T的距离,用于下一轮新的T的更新for (int j = 1; j <= n; j++) // 更新其他所有顶点到MST的最小距离if (!st[j]) dist[j] = min(dist[j], g[t][j]);}return res; // 返回最小生成树的总权重
}
例题:

#include<cstring>
#include<iostream>
#include<algorithm>using namespace std;const int N = 510,M = 100010,INF = 0x3f3f3f3f;int n,m;
int g[N][N];
int dist[N];
bool used[N];int prim(){memset(dist,0x3f,sizeof dist);int res = 0;for(int i = 0;i < n;i++){int t = -1;for(int j = 1;j <= n; j++){if((!used[j]) && (t == -1 || dist[t] > dist[j]))t = j;}used[t] = true;//第一步的dist[t]为INFif(i && dist[t] == INF) return INF;if(i)res += dist[t];for(int j = 1;j <= n;j++){if(!used[j])dist[j] = min(dist[j],g[t][j]);}}return res;
}int main(){scanf("%d%d",&n,&m);//重要memset(g,0x3f,sizeof(g));for(int i = 0;i < m; i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);g[u][v] = g[v][u] = min(g[u][v],w);}int r = prim();if(r == INF)puts("impossible");else printf("%d",r);return 0;
}1.3 堆优化的prim-不常用,且复杂,一般用kruskal替代
省略
二、最小生成树-kruskal算法
1.并查集复习
1.1 并查集(Union-Find)算法
是一个专门针对「动态连通性」的算法,我之前写过两次,因为这个算法的考察频率高,而且它也是最小生成树算法的前置知识
动态连通性
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:
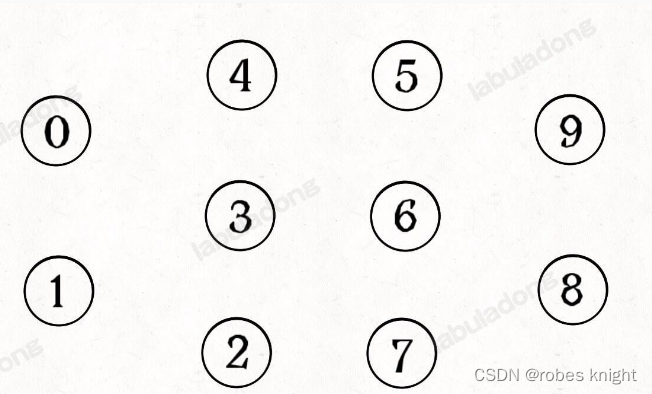
这里所说的「连通」是一种等价关系,也就是说具有如下三个性质:
1、自反性:节点 p 和 p 是连通的。
2、对称性:如果节点 p 和 q 连通,那么 q 和 p 也连通。
3、传递性:如果节点 p 和 q 连通,q 和 r 连通,那么 p 和 r 也连通。
现在我们的 Union-Find 算法主要需要实现这三个 API:
class UF {
public:/* 将 p 和 q 连接 */void union(int p, int q);/* 判断 p 和 q 是否连通 */bool connected(int p, int q);/* 返回图中有多少个连通分量 */int count();
};函数功能说明:
比如说之前那幅图,0~9 任意两个不同的点都不连通,调用 connected 都会返回 false,连通分量为 10 个。
如果现在调用 union(0, 1),那么 0 和 1 被连通,连通分量降为 9 个。
再调用 union(1, 2),这时 0,1,2 都被连通,调用 connected(0, 2) 也会返回 true,连通分量变为 8 个。

初始化:
怎么用森林来表示连通性呢?我们设定树的每个节点有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。比如说刚才那幅 10 个节点的图,一开始的时候没有相互连通,就是这样:

代码如下:
class UF {// 记录连通分量private:int count;// 节点 x 的父节点是 parent[x]int* parent;public:/* 构造函数,n 为图的节点总数 */UF(int n) {// 一开始互不连通this->count = n;// 父节点指针初始指向自己parent = new int[n];for (int i = 0; i < n; i++)parent[i] = i;}/* 其他函数 */
};union实现:
操作如下:
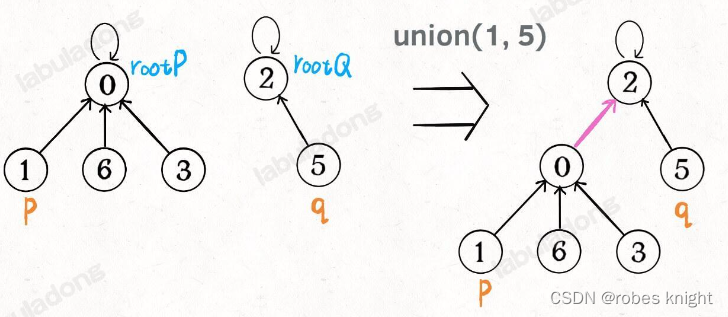
代码如下:
class UF {// 为了节约篇幅,省略上文给出的代码部分...public:void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;// 将两棵树合并为一棵parent[rootP] = rootQ;// parent[rootQ] = rootP 也一样count--; // 两个分量合二为一}/* 返回某个节点 x 的根节点 */int find(int x) {// 根节点的 parent[x] == xwhile (parent[x] != x)x = parent[x];return x;}/* 返回当前的连通分量个数 */int count() {return count;}
};connected实现:
代码如下:
class UF {
private:// 省略上文给出的代码部分...public:bool connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}
};1.2 平衡性优化-union优化
分析union和connected的时间复杂度,我们发现,主要 API connected和 union 中的复杂度都是 find 函数造成的,所以说它们的复杂度和 find 一样。
find 主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 logN,但这并不一定。logN 的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得「树」几乎退化成「链表」,树的高度最坏情况下可能变成 N。
图论解决的都是诸如社交网络这样数据规模巨大的问题,对于 union 和 connected 的调用非常频繁,每次调用需要线性时间完全不可忍受。
关键在于 union 过程,我们一开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:

长此以往,树可能生长得很不平衡。我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些。解决方法是额外使用一个 size 数组,记录每棵树包含的节点数,我们不妨称为「重量」:
class UF {
private:int count;int* parent;// 新增一个数组记录树的“重量”int* size;public:UF(int n) {this->count = n;parent = new int[n];// 最初每棵树只有一个节点// 重量应该初始化 1size = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;size[i] = 1;}}/* 其他函数 */
};比如说 size[3] = 5 表示,以节点 3 为根的那棵树,总共有 5 个节点。这样我们可以修改一下 union 方法:
class UF {
private:// 为了节约篇幅,省略上文给出的代码部分...
public:void union(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;// 小树接到大树下面,较平衡if (size[rootP] > size[rootQ]) {parent[rootQ] = rootP;size[rootP] += size[rootQ];} else {parent[rootP] = rootQ;size[rootQ] += size[rootP];}count--;}
};
这样,通过比较树的重量,就可以保证树的生长相对平衡,树的高度大致在 logN 这个数量级,极大提升执行效率。
此时,find , union , connected 的时间复杂度都下降为 O(logN),即便数据规模上亿,所需时间也非常少。
1.3 路径压缩-find优化
其实我们并不在乎每棵树的结构长什么样,只在乎根节点。
因为无论树长啥样,树上的每个节点的根节点都是相同的,所以能不能进一步压缩每棵树的高度,使树高始终保持为常数?

这样每个节点的父节点就是整棵树的根节点,find 就能以 O(1) 的时间找到某一节点的根节点,相应的,connected 和 union 复杂度都下降为 O(1)。
要做到这一点主要是修改 find 函数逻辑,非常简单,但你可能会看到两种不同的写法。
方法1:
class UF {// 为了节约篇幅,省略上文给出的代码部分...private:int find(int x) {while (parent[x] != x) {// 这行代码进行路径压缩parent[x] = parent[parent[x]];x = parent[x];}return x;}
};每次使得当前x指向父节点的父节点,这样会将一些节点向上移,然后缩短树的长度

压缩结束为:

方法二:
class UF {// 为了节约篇幅,省略上文给出的代码部分...// 第二种路径压缩的 find 方法public:int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}
};其迭代写法如下(便于理解):
int find(int x) {// 先找到根节点int root = x;while (parent[root] != root) {root = parent[root];}// 然后把 x 到根节点之间的所有节点直接接到根节点下面int old_parent = parent[x];while (x != root) {parent[x] = root;x = old_parent;old_parent = parent[old_parent];}return root;
}最终效果:

1.4 并查集框架-优化后
class UF {
private:// 连通分量个数int count;// 存储每个节点的父节点int *parent;public:// n 为图中节点的个数UF(int n) {this->count = n;parent = new int[n];for (int i = 0; i < n; i++) {parent[i] = i;}}// 将节点 p 和节点 q 连通void union_(int p, int q) {int rootP = find(p);int rootQ = find(q);if (rootP == rootQ)return;parent[rootQ] = rootP;// 两个连通分量合并成一个连通分量count--;}// 判断节点 p 和节点 q 是否连通bool connected(int p, int q) {int rootP = find(p);int rootQ = find(q);return rootP == rootQ;}int find(int x) {if (parent[x] != x) {parent[x] = find(parent[x]);}return parent[x];}// 返回图中的连通分量个数int count_() {return count;}
};2.kruskal
给你输入编号从 0 到 n - 1 的 n 个结点,和一个无向边列表 edges(每条边用节点二元组表示),请你判断输入的这些边组成的结构是否是一棵树。
如果输入:
n = 5
edges = [[0,1], [0,2], [0,3], [1,4]]这些边构成的是一棵树,算法应该返回 true:

输入:
n = 5
edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]形成的就不是树结构了,因为包含环:

我们思考为何会产生环?仔细体会下面两种添边的差别

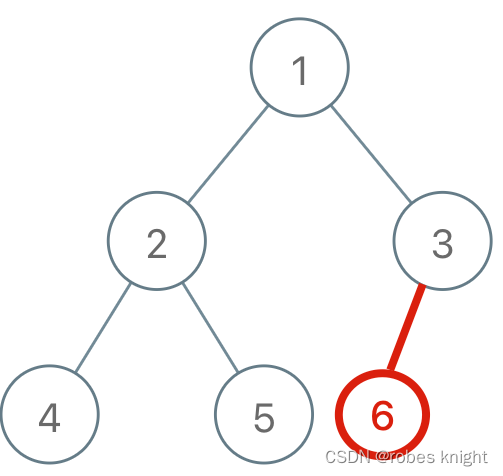
总结一下规律就是:
对于添加的这条边,如果该边的两个节点本来就在同一连通分量里,那么添加这条边会产生环;反之,如果该边的两个节点不在同一连通分量里,则添加这条边不会产生环。
那么只需要在union两节点之前先检测两节点是否已经connection,如果已连接所有添加后会生成环,则返回false。同时需要注意count==1,不然就是森林了。
代码如下:
class UF {
public:vector<int> parent;UF(int n) {for (int i = 0; i < n; i++) {parent.push_back(i);}}int find(int x) {while (x != parent[x]) {parent[x] = parent[parent[x]];x = parent[x];}return x;}void union_(int p, int q) {int root_p = find(p);int root_q = find(q);parent[root_p] = root_q;}bool connected(int p, int q) {int root_p = find(p);int root_q = find(q);return root_p == root_q;}int count() {int cnt = 0;for (int i = 0; i < parent.size(); i++) {if (parent[i] == i) {cnt++;}}return cnt;}
};bool validTree(int n, vector<vector<int>>& edges) {UF uf(n);// 遍历所有边,将组成边的两个节点进行连接for (auto edge : edges) {int u = edge[0];int v = edge[1];// 若两个节点已经在同一连通分量中,会产生环if (uf.connected(u, v)) {return false;}// 这条边不会产生环,可以是树的一部分uf.union_(u, v);}// 要保证最后只形成了一棵树,即只有一个连通分量return uf.count() == 1;
}3.连接所有点的最小费用-kruskal算法
所谓最小生成树,就是图中若干边的集合(我们后文称这个集合为 mst,最小生成树的英文缩写),你要保证这些边:
1、包含图中的所有节点。
2、形成的结构是树结构(即不存在环)。
3、权重和最小。
有之前题目的铺垫,前两条其实可以很容易地利用 Union-Find 算法做到,关键在于第 3 点,如何保证得到的这棵生成树是权重和最小的。
这里就用到了贪心思路:
将所有边按照权重从小到大排序,从权重最小的边开始遍历,如果这条边和 mst 中的其它边不会形成环,则这条边是最小生成树的一部分,将它加入 mst 集合;否则,这条边不是最小生成树的一部分,不要把它加入 mst 集合。
以此题为例:
 此题虽然是使用kruskal算法,但是并不是直接套用,还要有一些值得注意的事项
此题虽然是使用kruskal算法,但是并不是直接套用,还要有一些值得注意的事项
1:我们要将题目中的给出点,转换为点组合并且将权重添加进去
在题中只给出一个点的坐标,我们需要想方法转换为两个点的链接,所以需要将每个点(两个坐标组合)转换为一个符号标记,在链接数组把相连的两个符号放一起就行了,很明显,我们使用0-n-1来记录每一个点是最合适的,不仅方便遍历也一目了然
因此有如下代码:
vector<vector<int>> edges;for(int i =0;i < points.size();i++){//此处不能写为int j = 0,这样会重复导致超时,根据求子集的思想,应该从j=i+1开始for(int j = i+1;j < points.size();j++){// if(i == j)continue;//因为j=i+1开始,所有不需要这句判断int w1 = abs(points[i][0]-points[j][0]);int w2 = abs(points[i][1]-points[j][1]);edges.push_back({i,j,w1+w2});}}2:我们要对得到的数组进行排序,而且是对权重维度排序,这就需要我们利用lambda来自定义sort的排序方式了
有代码如下:
sort(edges.begin(),edges.end(),[](const vector<int>& a,const vector<int>& b){return a[2] < b[2];});依照kruskal算法,可以写出如下完整代码:
class uf{private:int count;vector<int> parent;public:uf(int n){this->count = n;// parent = new int[n];parent.resize(n);for(int i=0;i < n;i++){parent[i] = i;}}int find(int x){if(parent[x]!=x)parent[x] = find(parent[x]);return parent[x];}void Union(int p,int q){int rootp = find(p);int rootq = find(q);if(rootp == rootq)return;parent[rootp] = rootq;count--;}bool connection(int p,int q){int rootp = find(p);int rootq = find(q);return rootp == rootq;}
};class Solution {
public:int minCostConnectPoints(vector<vector<int>>& points) {vector<vector<int>> edges;for(int i =0;i < points.size();i++){//此处不能写为int j = 0,这样会重复导致超时,根据求子集的思想,应该从j=i+1开始for(int j = i+1;j < points.size();j++){// if(i == j)continue;//因为j=i+1开始,所有不需要这句判断int w1 = abs(points[i][0]-points[j][0]);int w2 = abs(points[i][1]-points[j][1]);edges.push_back({i,j,w1+w2});}}sort(edges.begin(),edges.end(),[](const vector<int>& a,const vector<int>& b){return a[2] < b[2];});uf uf(points.size());int sum_w = 0;for(auto& s : edges){int q = s[0],p = s[1],w = s[2];if(uf.connection(p,q))continue;sum_w +=w;uf.Union(p,q);}return sum_w;}
};
相关文章:

图论- 最小生成树
一、最小生成树-prim算法 1.1 最小生成树概念 一幅图可以有很多不同的生成树,比如下面这幅图,红色的边就组成了两棵不同的生成树: 对于加权图,每条边都有权重(用最小生成树算法的现实场景中,图的边权重…...
LeetCode刷题记(一):1~30题
1. 两数之和 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你可以…...
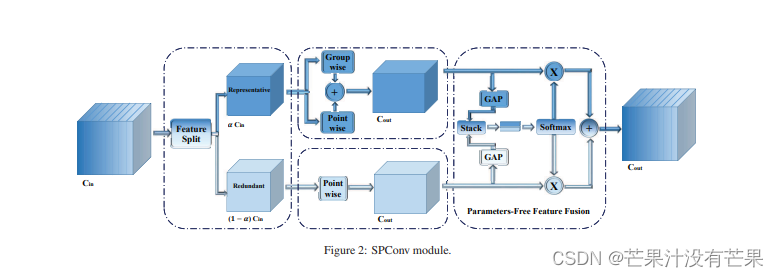
芒果YOLOv5改进89:卷积SPConv篇,即插即用,去除特征图中的冗余,FLOPs 和参数急剧下降,提升小目标检测
芒果专栏 基于 SPConv 的改进结构,改进源码教程 | 详情如下🥇 👉1. SPConv 结构、👉2. CfSPConv 结构 💡本博客 改进源代码改进 适用于 YOLOv5 按步骤操作运行改进后的代码即可 即插即用 结构。博客 包括改进所需的 核心结构代码 文件 YOLOv5改进专栏完整目录链接:…...
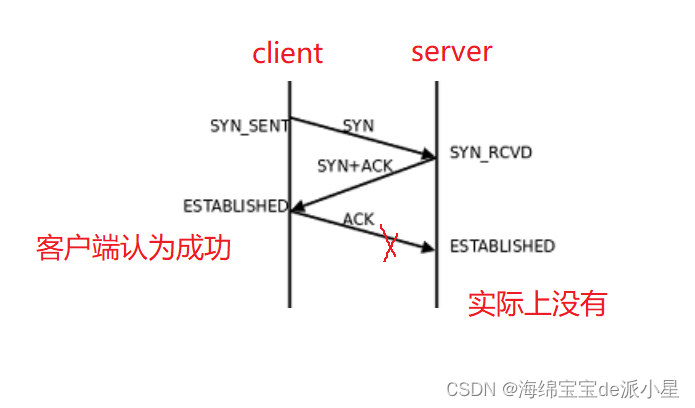
Linux:详解TCP报头类型
文章目录 温习序号的意义序号和确认序号报文的类型 TCP报头类型详解ACK: 确认号是否有效SYN: 请求建立连接; 我们把携带SYN标识的称为同步报文段FIN: 通知对方, 本端要关闭了PSH: 提示接收端应用程序立刻从TCP缓冲区把数据读走RST: 对方要求重新建立连接; 我们把携带RST标识的称…...
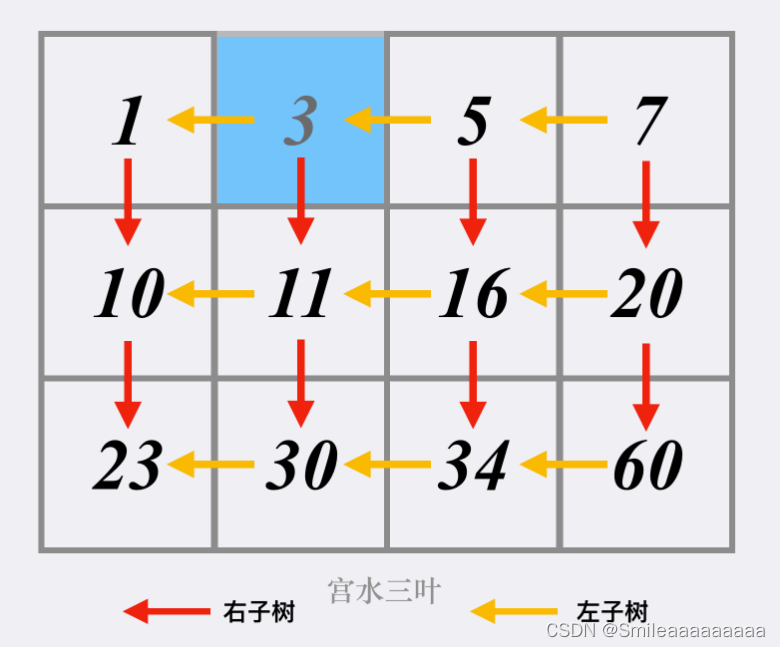
【Leetcode】top 100 二分查找
35 搜索插入位置 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。请必须使用时间复杂度为 O(log n) 的算法。 基础写法!!!牢记…...
Redis高级面试题-2024
说说你对Redis的理解 Redis是一个基于Key-Value存储结构的开源内存数据库,也是一种NoSQL数据库。 它支持多种数据类型,包括String、Map、Set、ZSet和List,以满足不同应用场景的需求。 Redis以内存存储和优化的数据结构为基础,提…...

HarmonyOS 应用开发之FA模型与Stage模型应用组件
应用配置文件概述(FA模型) 每个应用项目必须在项目的代码目录下加入配置文件,这些配置文件会向编译工具、操作系统和应用市场提供描述应用的基本信息。 应用配置文件需申明以下内容: 应用的软件Bundle名称,应用的开发…...

6个黑科技网站,永久免费
1、http://mfsc123.com https://www.mfsc123.com 一个非常赞的免费商用素材导航网站。 收集了各种免费、免版权的图片、插画、视频、视频模板、音乐、音效、字体、图标网站。 再也不用担心版权问题,都能免费商用,自媒体作者必备。 而且还在每个网站…...

Linux 内核优化简笔 - 高并发的系统
简介 Linux 服务器在高并发场景下,默认的内核参数无法利用现有硬件,造成软件崩溃、卡顿、性能瓶颈。 当然,修改参数只是让Linux更好软件的去利用已有的硬件资源,如果硬件资源不够也无法解决问题的。而且当硬件资源不足的时候&am…...
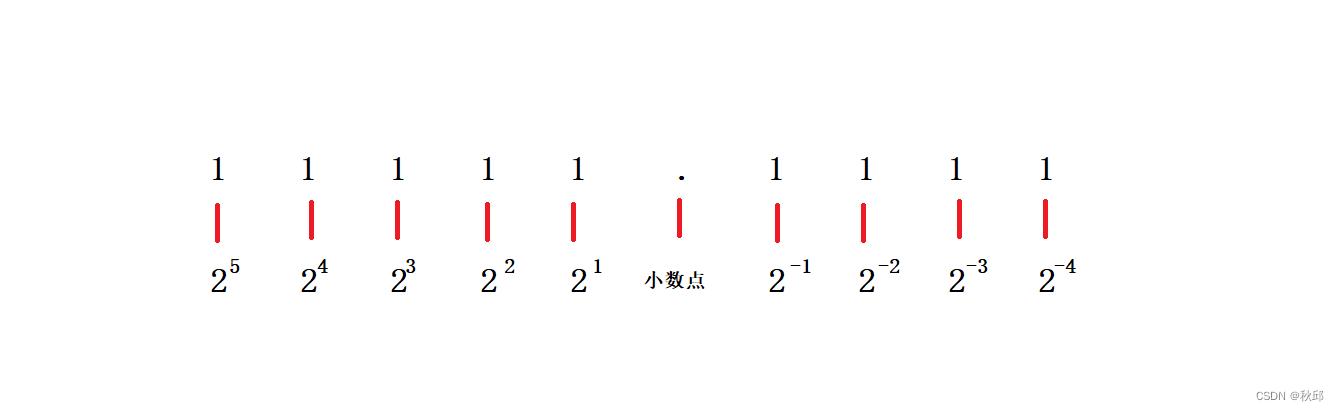
整型之韵,数之舞:大小端与浮点数的内存之旅
✨✨欢迎👍👍点赞☕️☕️收藏✍✍评论 个人主页:秋邱’博客 所属栏目:人工智能 (感谢您的光临,您的光临蓬荜生辉) 1.0 整形提升 我们先来看看代码。 int main() {char a 3;char b 127;char …...

变量作用域
变量作用域 标识符的作用域是定义为其声明在程序里的可应用范围, 或者即是我们所说的变量可见性。换句话说,就好像在问你自己,你可以在程序里的哪些部分去访问一个制定的标识符。变量可以是局部域或者全局域。 全局变量与局部变量 定义在函数内的变量有局部作用域,在一个…...
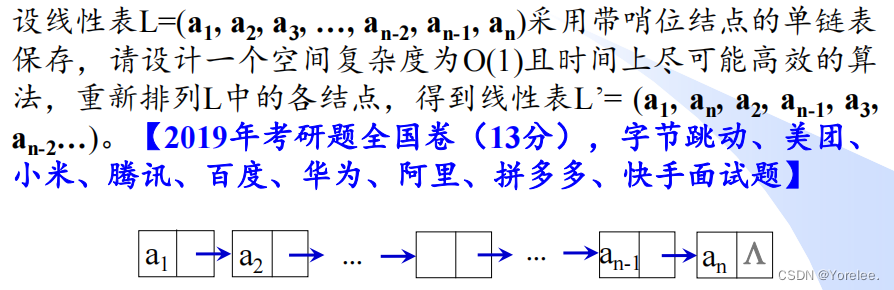
数据结构:链表的双指针技巧
文章目录 一、链表相交问题二、单链表判环问题三、回文链表四、重排链表结点 初学双指针的同学,请先弄懂删除链表的倒数第 N 个结点。 并且在学习这一节时,不要将思维固化,认为只能这样做,这里的做法只是技巧。 一、链表相交问题 …...

用WHERE命令可以在命令行搜索文件
文章目录 用WHERE命令可以在命令行搜索文件概述笔记没用的小程序END 用WHERE命令可以在命令行搜索文件 概述 想确认PATH变量中是否存在某个指定的程序(具体是在PATH环境变量中给出的哪个路径底下?). 开始不知道windows有where这个命令, 还自己花了2个小时写了一个小程序. 后…...

持续交付/持续部署流水线介绍(CD)
目录 一、概述 二、典型操作流程 2.1 CI/CD典型操作流 2.2 CI/CD操作流程说明 2.3 总结 三、基于GitHubDocker的持续交付/持续部署流水线(公有云) 3.1 基于GitHubDocker的持续交付/持续部署操作流程示意图 3.2 GitHubDocker持续交付/持续部署流水…...

第四百三十八回
文章目录 1. 概念介绍2. 思路与方法2.1 实现思路2.2 实现方法 3. 示例代码4. 内容总结 们在上一章回中介绍了"不同平台上换行的问题"相关的内容,本章回中将介绍如何在页面上显示蒙板层.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们…...

Python学习:面相对象
面向对象 面向对象技术简介 类(Class): 用来描述具有相同的属性和方法的对象的集合。它定义了该集合中每个对象所共有的属性和方法。对象是类的实例。方法:类中定义的函数。类变量:类变量在整个实例化的对象中是公用的。类变量定义在类中且在函数体之外。类变量通常不作为实…...
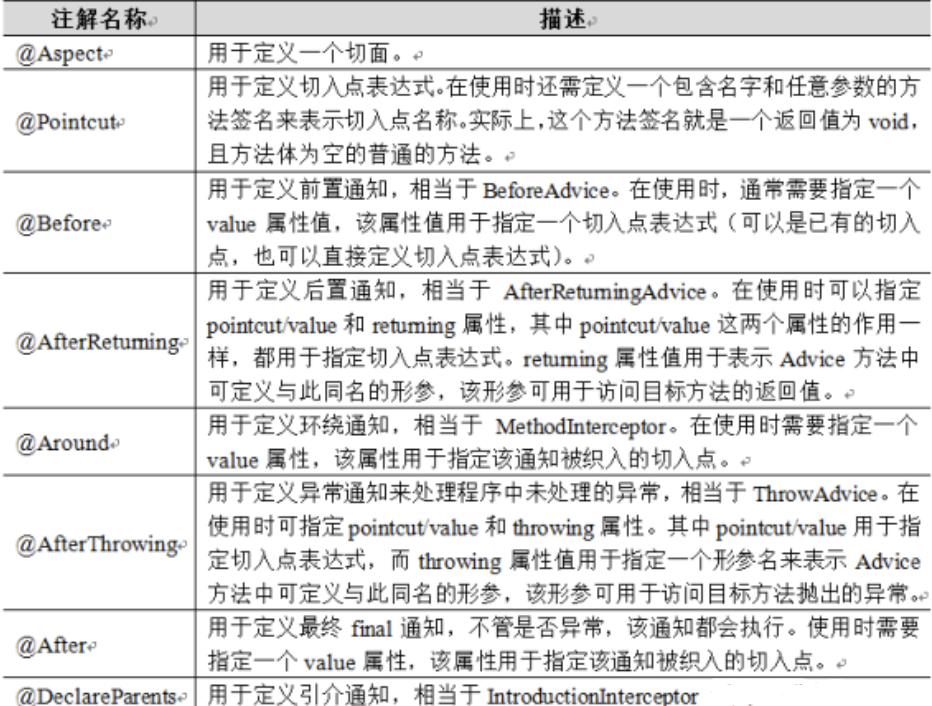
SSM学习——Spring AOP与AspectJ
Spring AOP与AspectJ 概念 AOP的全称为Aspect-Oriented Programming,即面向切面编程。 想象你是汉堡店的厨师,每一份汉堡都有好几层,这每一层都可以视作一个切面。现在有一位顾客想要品尝到不同风味肉馅的汉堡,如果按照传统的方…...

Android 使用LeakCanary检测内存泄漏,分析原因
内存泄漏是指无用对象(不再使用的对象)持续占有内存或无用对象的内存得不到及时释放,从而造成内存空间的浪费称为内存泄漏。 平时我们在使用app时,少量的内存泄漏我们是发现不了的,但是当内存泄漏达到一定数量时&…...
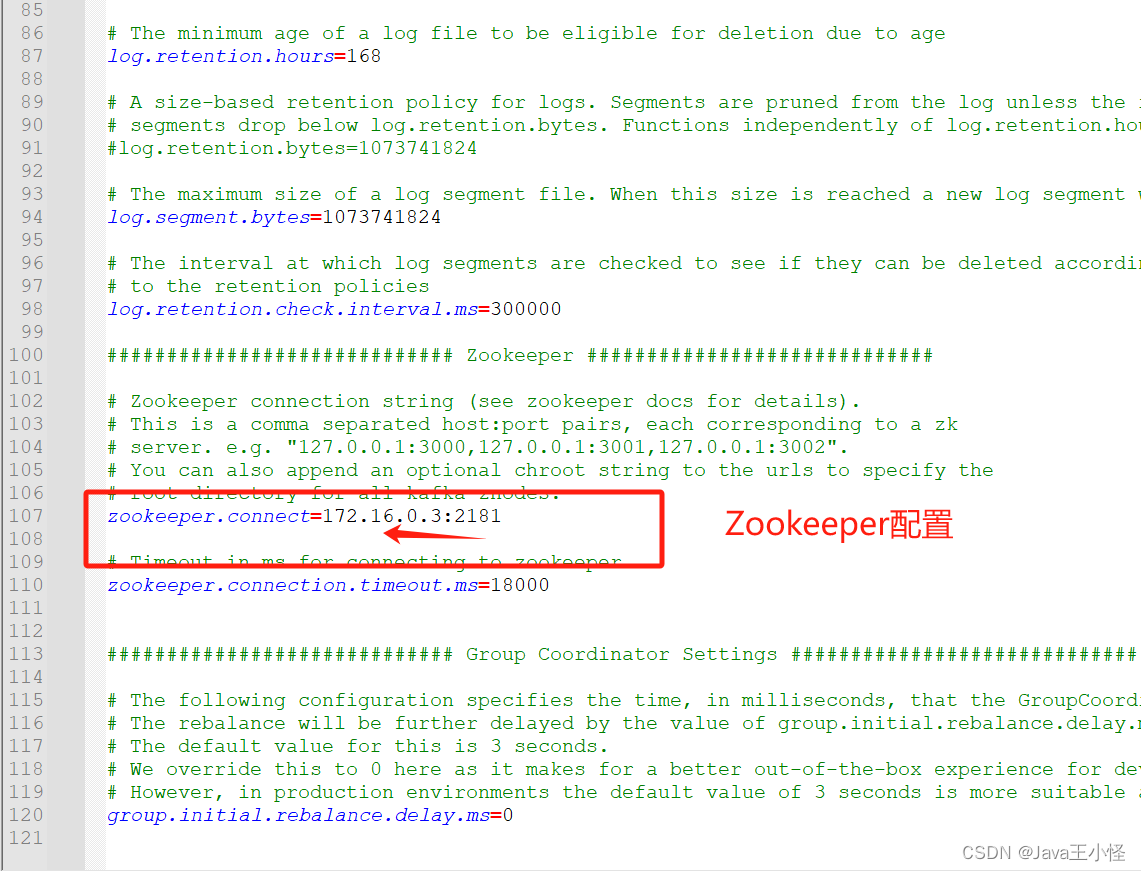
Linux部署Kafka2.8.1
安装Jdk 首先确保你的机器上安装了Jdk,Kafka需要Java运行环境,低版本的Kafka还需要Zookeeper,我此次要安装的Kafka版本为2.8.1,已经内置了一个Zookeeper环境,所以我们可以不部署Zookeeper直接使用。 1、解压Jdk包 t…...
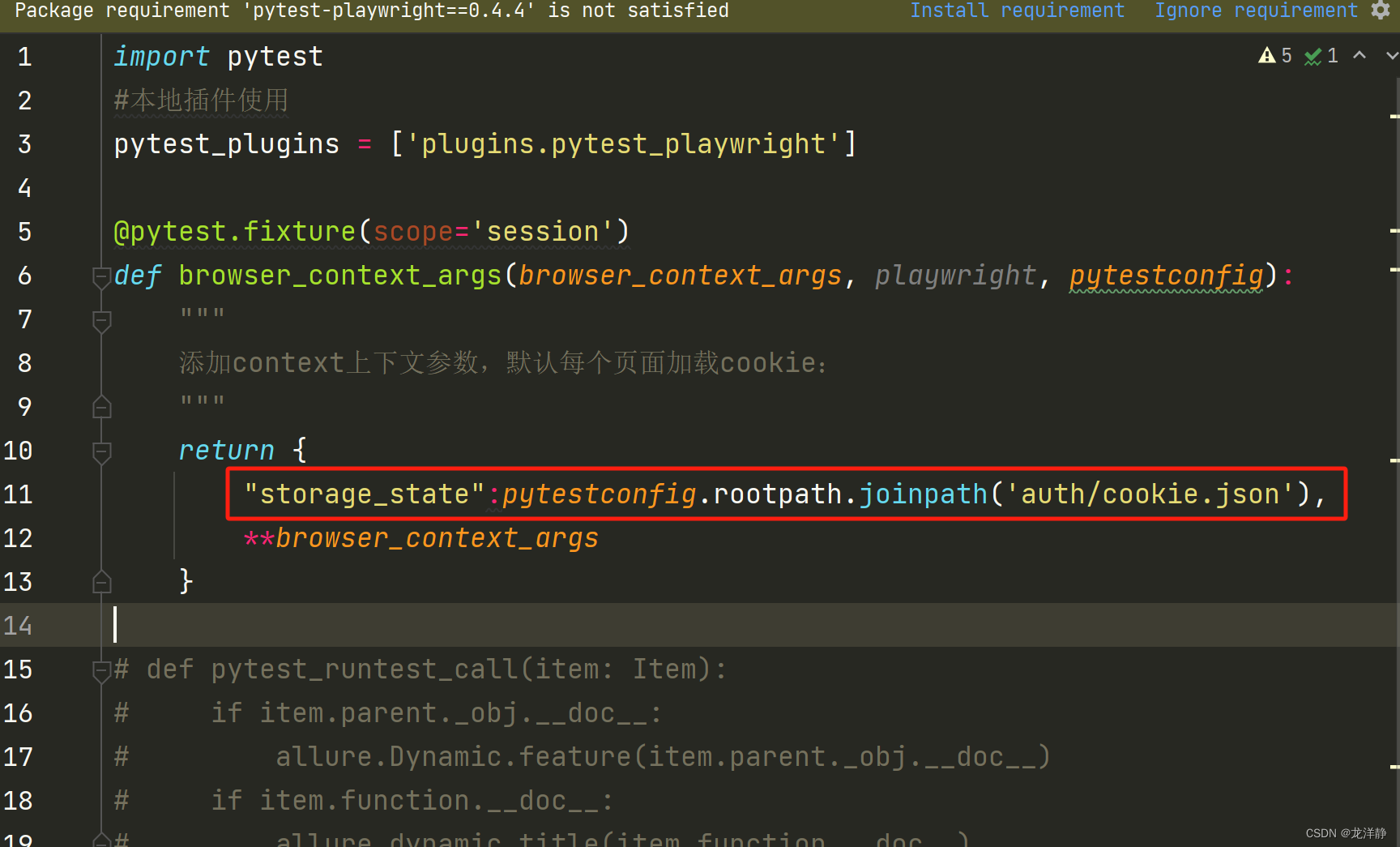
【pytest、playwright】allure报告生成视频和图片
目录 1、修改插件pytest_playwright 2、conftest.py配置 3、修改pytest.ini文件 4、运行case 5、注意事项 1、修改插件pytest_playwright pytest_playwright.py内容如下: # Copyright (c) Microsoft Corporation. # # Licensed under the Apache License, Ver…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...