判断点在多边形内的算法
在计算几何中,判定点是否在多边形内,是个非常有趣的问题。通常有两种方法:
一、Crossing Number(交叉数)
它计算从点P开始的射线穿过多边形边界的次数。当“交叉数”是偶数时,点在外面;当它是奇数时,点在里面。这种方法有时被称为“奇-偶”检验。
如果一个多边形是不自交的(称为“简单多边形”),那么这两种方法对任意点都给出相同的结果。但对于非简单多边形,这两种方法在某些情况下会给出不同的答案。如下图所示,当一个多边形与自身重叠时,对于重叠区域内的点,如果使用交叉数判断,它在外面;而使用环绕数判断则在里面。
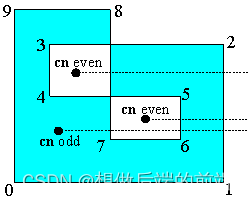
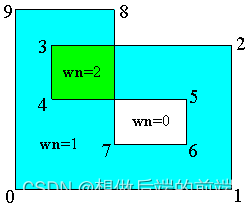
在上图中,绿色区域中的点,wn = 2,表示在多边形中重叠了2次。相比于Crossing number,winding number给出了更内蕴性的答案。
尽管如此,早些时候,crossing number方法应用的更广泛,因为最初计算几何专家们错误地认为crossing number比winding number计算起来更加高效。但事实并非如此,两者的时间复杂度完全一样。Franklin在2000年给出一个计算winding number的非常快的实现。因此,为了几何正确性和效率的原因,在确定一个多边形中的一个点时,wn算法应该总是首选的。
该方法计算从点P开始的射线穿过多边形边界的次数(不管穿过的方向)。如果这个数是偶数,那么点在外面;否则,当交叉数为奇数时,点在多边形内。其正确性很容易理解,因为每次射线穿过多边形边缘时,它的内外奇偶性都会发生变化(因为边界总是分隔内外)。最终,任何射线都在边界多边形之外结束。所以,如果点在多边形内,那么对边界的穿过次序一定是:out>…>in>out,因此交叉数一定是奇数;同样地,如果点在多边形外,那么对边界的穿过次序一定是in > out … > in > out,因此交叉数必是偶数。
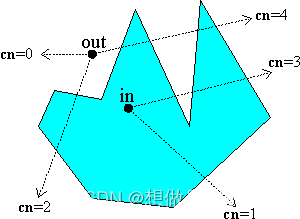 在实现crossing number的算法时,必须确保只计算改变奇偶性的交叉位置。特别是,对于射线穿过顶点的情况需要适当的处理。下图列举了射线与多边形可能的相交情况:
在实现crossing number的算法时,必须确保只计算改变奇偶性的交叉位置。特别是,对于射线穿过顶点的情况需要适当的处理。下图列举了射线与多边形可能的相交情况:

此外,必须确定多边形边界上的点P是在内部还是外部。一般约定:如果点在边的左侧,那么认为点P在内部;如果点在边的右侧,那么认为点P在外部。如果两个不同的多边形共享一个共同的边界线段,那么该线段上的一点将会在一个多边形或另一个多边形中,而不是同时在两个多边形中。这避免了许多可能发生的问题,特别是在计算机图形显示中。
一个简单的做法是选择一条x轴正方向的水平射线,对于这样一条射线,很容易计算多边形的边与它的交点。而且,很容易确定交点是否存在。算法只需沿着多边形的每一条边,依次计算交点,当相交时,cn增加1,从而计算出最终的总交叉数。
此外,相交测试必须遵循如下的规则,处理一些特殊情况(如上图):
- 向上的边,包含起点,但不包含终点;
- 向下的边,包含终点,但不包含起点;
- 水平的边,不包含起点和终点;
- 边与射线的交点必须严格在点P的右侧
按照上述规则,处理特殊的相交情况,就能得到正确的交叉数。其中,规则4将导致在边界右侧的点在多边形外部,在左侧的点将会被判定为在内部。
Crossing Number Pseudo-Code:
对于n个点组成的多边形V={V[0], V[1], …,V[n]},其中V[n]=V[0], 计算几何大牛Franklin给出了一个非常有名的实现:
typedef struct {int x, y;} Point;cn_PnPoly( Point P, Point V[], int n )
{int cn = 0; // the crossing number counter// loop through all edges of the polygonfor (each edge E[i]:V[i]V[i+1] of the polygon) {if (E[i] crosses upward ala Rule #1|| E[i] crosses downward ala Rule #2) {if (P.x < x_intersect of E[i] with y=P.y) // Rule #4++cn; // a valid crossing to the right of P.x}}return (cn&1); // 0 if even (out), and 1 if odd (in)}
注意,对于满足规则1和2的向上和向下交叉的测试也排除了水平边缘(规则3)。总而言之,很多工作是通过几个测试完成的,这使得这个算法很优雅。
然而,交叉数方法的有效性是基于“约当曲线定理”(Jordan Curve Theorem),该定理表明,一条简单的闭合曲线将二维平面分成两个完全连通的分量:一个有界的“内”分量和一个无界的“外”分量。需要注意的是,曲线必须是简单的(没有自身交叉),否则可能有两个以上的组成部分,然后就不能保证跨越边界改变进出奇偶性。因此,该方法不适用于自相交的多边形。
二、Winding Number(环绕数)
它计算多边形绕着点P旋转的次数。只有当“圈数”wn = 0时,点才在外面; 否则,点在里面。
winding number方法能准确判定一个点是否在自交的封闭曲线内。该方法通过计算多边形有多少次环绕点P来实现。只有当多边形不环绕该点,也就是环绕数wn = 0时,一个点才在外面。
不妨定义:平面上的点P相对于任意连续封闭曲线的环绕数为{wn}(P,C)。对于一条水平向右的射线R,我们每一条与R相交的边需要判断其终点在R上面还是下面。如果边从下往上穿过R,wn+1;否则wn-1。所有边遍历一遍,最终得到总的f{wn}(P,C),如下图所示:
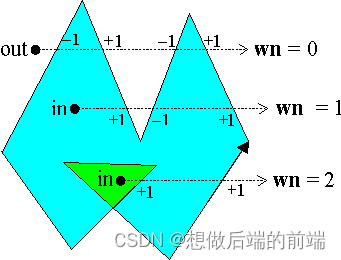
此外,我们没必要计算实际的交点,只需要使用如下方法判断当前穿过的边的环绕数应该+1还是-1:
如下图所示,如果一条边向上穿过射线R,那么P点在边ViVi+1的左侧;而对于一条向下的边,P点在边ViVi+1的右侧。

通过以上分析,容易给出如下的wn计算伪代码(和cn的计算一样使用相同的边相交规则):
typedef struct {int x, y;} Point;wn_PnPoly( Point P, Point V[], int n )
{int wn = 0; // the winding number counter// loop through all edges of the polygonfor (each edge E[i]:V[i]V[i+1] of the polygon) {if (E[i] crosses upward ala Rule #1) {if (P is strictly left of E[i]) // Rule #4++wn; // a valid up intersect right of P.x}elseif (E[i] crosses downward ala Rule #2) {if (P is strictly right of E[i]) // Rule #4--wn; // a valid down intersect right of P.x}}return wn; // =0 <=> P is outside the polygon}
显然,环绕数方法与交叉数方法有着相同的计算效率。但由于该方法更加具有普遍性,因此,在确定一个点是否在任意多边形内时,推荐使用Winding Number方法。
通过一些技巧可以进一步提高wn算法的效率,在下面给出的wn_PnPoly() 的实现中,我们可以看到这一点。在该代码中,所有完全在P以上或完全在P以下的边只经过两次不等式检验就被拒绝(没有交点)。然而,在目前流行的cn算法的实现中,需要3次不等式检验才能做到这一点。由于在实际应用中,大多数边都会被拒绝,因此进行比较的次数减少了大约33%(或更多)。在使用非常大的(1,000,000边)随机多边形(边长<多边形直径的1/10)和1000个随机测试点(在多边形的边界内)进行运行时测试时,测试结果表明wn算法的平均效率提高了20%。
相关文章:

判断点在多边形内的算法
在计算几何中,判定点是否在多边形内,是个非常有趣的问题。通常有两种方法: 一、Crossing Number(交叉数) 它计算从点P开始的射线穿过多边形边界的次数。当“交叉数”是偶数时,点在外面;当它是奇数时&…...

Network AIS Receiver R400N
目录 Introduction OVERVIEW BASIC FEATURES APPLICATIONS SPECIFICATIONS Introduction OVERVIEW The R400N provides a method of monitoring the position, speed and heading of AIS vessels within VHF range. It can decode of Class A, Class B, Aids to Navigat…...

JavaScript循环
JavaScript的循环有两种,一种是for循环,通过初始条件、结束条件和递增条件来循环执行语句块: var x 0; var i; for (i1; i<10000; i) { x x i; } x; // 50005000 for循环的3个条件都是可以省略的,如果没有退出循环的判断条件…...

9Proxy,跨境电商一站式解决方案
文章目录 跨境电商什么是跨境电商跨境电商的机遇跨境电商技术支撑 海外代理IP什么是海外代理IP海外代理IP的作用如何选择海外代理IP 9Proxy9Proxy的优势9Proxy的解决方案价格汇总搜索引擎优化市场调查多重核算数据抓取广告技术 价格上手体验注册登录下载安装数据采集 总结福利 …...
ObjectiveC-08-OOP面向对象程序设计-类的分离与组合
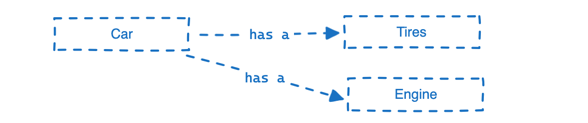
本节用一简短的文章来说下是ObjectiveC中的类。类其实是OOP中的一个概念,概念上简单来讲类是它是一组关系密切属性的集合,所谓的关系就是对现实事物的抽象。 上面提到的关系包括很多种,比如has a, is a,has some等&…...

Qt 总结
由于工作需要用到Qt。把过程中学习到的东西记录下来,希望能帮到他人和将来的自己。 由于需要快速实现需求,所以对Qt只是使用,并没有对原理的深入理解。 故此文只适合入门,不适合深入学习Qt。 文章目录 安装&维护示例&教…...
中间件复习之-RPC框架
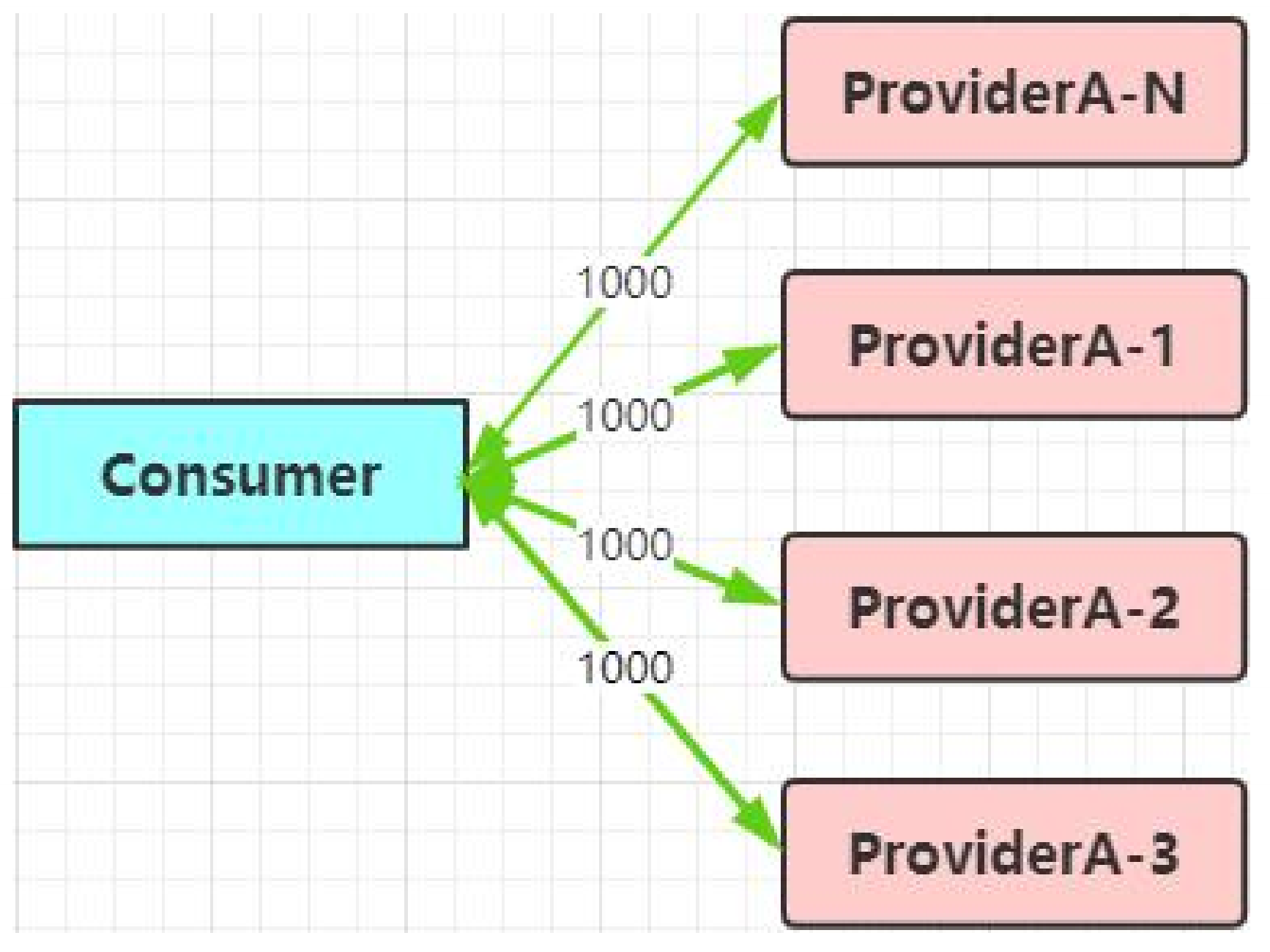
什么是RPC框架? RPC(Remote Procedure Call):远程过程调用。当多个应用部署在多个服务器上时,由于他们不在一个内存空间上,因此需要网络来进行通信,而RPC允许它像调用本地方法一样调用远程服务。 RPC原理 服务消费方通过RPC客户…...

AcWing 787. 归并排序——算法基础课题解
AcWing 787. 归并排序 文章目录 题目描述CGo模板 题目描述 给定你一个长度为 n 的整数数列。 请你使用归并排序对这个数列按照从小到大进行排序。 并将排好序的数列按顺序输出。 输入格式 输入共两行,第一行包含整数 n。 第二行包含 n 个整数(所有…...
力扣1379---找出克隆二叉树的相同节点(Java、DFS、简单题)
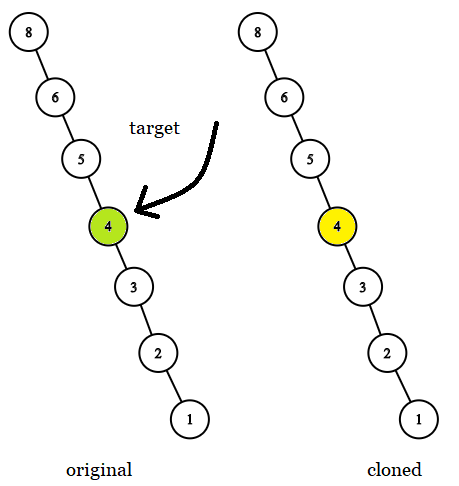
目录 题目描述: 思路描述: 代码: (1): (2): 题目描述: 给你两棵二叉树,原始树 original 和克隆树 cloned,以及一个位于原始树 ori…...
FLink学习(三)-DataStream
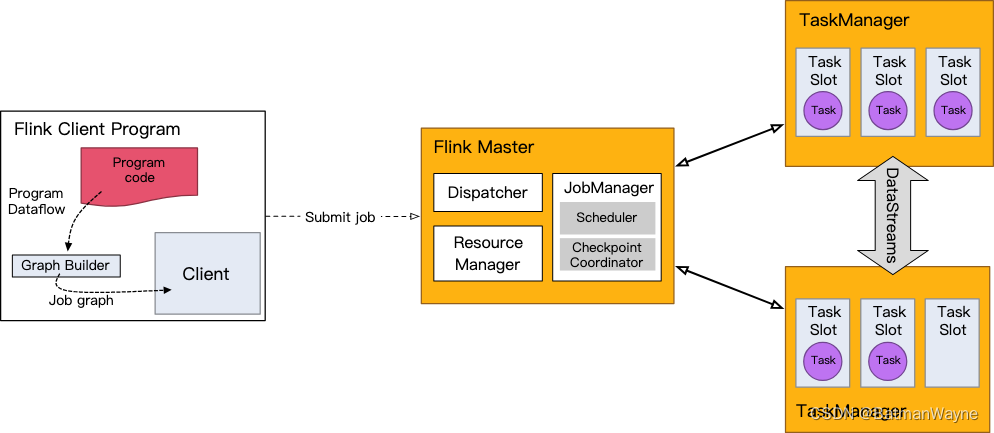
一、DataStream 1,支持序列化的类型有 基本类型,即 String、Long、Integer、Boolean、Array复合类型:Tuples、POJOs 和 Scala case classes Tuples Flink 自带有 Tuple0 到 Tuple25 类型 Tuple2<String, Integer> person Tuple2.…...
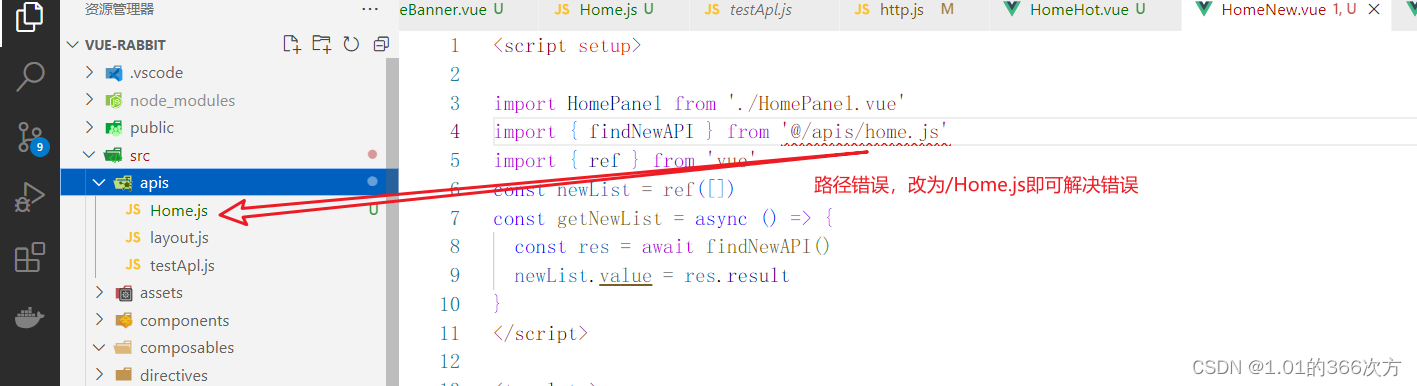
Failed to resolve import “Home/components/HomeNew.vue“. Does the file exist?
错误信息 [plugin:vite:import-analysis] Failed to resolve import "/apis/home.js" from "src/views/Home/components/HomeNew.vue". Does the file exist? 错误原因 路径错误 解决方法...

《价值》-张磊-高瓴资本-3-建立人脉和信任;顺应趋势,把握机遇;
第三章 价值投资初试炼 2005.6.1 创办高瓴资本 许多人问我为什么一直在创业,其实我倒没想到自己非要创业成功不可,只是觉得一定要做点事,做点有意义的事。归根到底,可能是“爱折腾,不满足现状,爱挑战自己”…...

游戏引擎中的物理应用
一、 角色控制器 Character Controller和普通的动态对象(Dynamic Actor )是不同的,主要的三个特点是: 它拥有可控制的刚体间的交互假设它是有无穷的摩擦力(可以站停在位置上),没有弹性加速和刹车几乎立即…...

复现k8s黄金票据学习
1.什么是黄金票据 在 Kubernetes 中,"黄金票据"并不是一个常见的术语。可能你想了解的是服务账户(Service Account)。服务账户是 Kubernetes 中用于身份验证和授权的一种机制。它们允许 Pods 或其他工作负载在 Kubernetes 集群中与…...

08-JavaScript BOM定时器及JS动画
1. 设置定时器 1.1设置超时定时器 超时调用需要使用window对象的setTimeout()方法,该方法接受两个参数:调用函数或计算表达式和以毫秒为单位的时间(即在执行代码前需要等待多少毫秒)。 //setTimeout(callback, after) //callba…...
边缘计算盒子与云计算:谁更适合您的业务需求?
边缘计算盒子和云计算,这两个概念听起来可能有点复杂,但其实它们就是两种不同的数据处理方式。那谁更适合您的业务需求呢?咱们来详细说说。 边缘计算盒子,就像是个小型的数据处理中心,放在离你业务现场比较近的地方。它…...
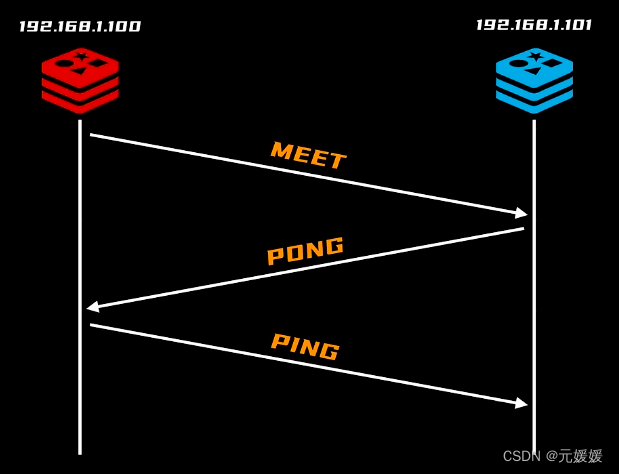
浅聊什么是Redis?
需求:MySQL面临大量的查询,即读写操作,因此类比CPU,给数据加缓存,Redis诞生。应用程序从MySQL查询的数据,在Redis设置缓存(记录在内存中,无需IO操作),后再需要…...

java算法day43 | ● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零
1049. 最后一块石头的重量 II 核心思想: 尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。 是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。那么分成两堆石头,一堆石头的…...

练气第六天
问:ANR怎么分析? ANR问题,这其实是一个非常综合性的问题,因为anr会涉及CPU负载,内存空间大小,线程锁,GC回收,这里面每个点,都是非常考验我们基本功的。 分析ANR问题,需…...

认识 Redis 与 分布式
Redis 官网页面 Redis官网链接 Redis 的简介 Redis 是一个在内存中存储数据的中间件 一方面用于作为数据库,另一方面用于作为数据缓存,适用于分布式系统中 Redis 基于网络,进行进程间通信,把自己内存中的变量给别的进程…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...
