2024.3.2力扣每日一题——受限条件下可到达节点的数目
2024.3.2
- 题目来源
- 我的题解
- 方法一 深度优先搜索
- 方法二 并查集
题目来源
力扣每日一题;题序:2368
我的题解
方法一 深度优先搜索
使用深度优先搜索实现,在搜索过程中根据restricted进行截停。
时间复杂度:O(n)
空间复杂度:O(n)
int res=0;
public int reachableNodes(int n, int[][] edges, int[] restricted) {List<Integer>[] g=createTree(n,edges);boolean[] bRestricted=new boolean[n];for(int i:restricted){bRestricted[i]=true;}dfs(g,0,-1,bRestricted);return res;
}
public List<Integer>[] createTree(int n,int[][] edges){List<Integer>[] g=new ArrayList[n];for(int i=0;i<n;i++){g[i]=new ArrayList<>();}for(int[] t:edges){int from = t[0];int to = t[1];g[from].add(to);g[to].add(from);}return g;
}
public void dfs(List<Integer>[] g,int cur,int pre,boolean[] bRestricted){res++;for(int next:g[cur]){//防止循环遍历 并且不能是受限节点if(next!=pre&&!bRestricted[next])dfs(g,next,cur,bRestricted);}
}
方法二 并查集
如果忽略受限的点,树就会变成若干个连通块,要计算的就是 0号点所在连通块的大小。
因此,可以用并查集来不断地将点集进行合并,依次考虑每一条边,如果边上两个点都没有受限,那么合并这两个点的所在集合,否则跳过该边。最终查询 0号点所在连通块的大小即可。
时间复杂度:O(n×α(n)),其中 n 是无向树中点的个数,α是反阿克曼函数。使用路径压缩和按秩合并优化后的并查集,单次查询和合并操作的时间复杂度是 O(α(n)),通常比较小,可以忽略。
空间复杂度:O(n)
public int reachableNodes(int n, int[][] edges, int[] restricted) {boolean[] bRestricted=new boolean[n];for(int i:restricted){bRestricted[i]=true;}UF uf=new UF(n);for(int[] v:edges){//如果起始和结束节点有一个是受限的节点,则不合并if(bRestricted[v[0]]||bRestricted[v[1]]){continue;}uf.union(v[0],v[1]);}return uf.getCount();
}
class UF{private int count;private int parent[];public UF(int n){count=n;parent=new int[n];for (int i = 0; i < n; i++) {parent[i]=i;}}public void union(int p,int q){int parentP=find(p);int parentQ=find(q);if (parentP==parentQ)return;parent[parentQ]=parentP;count--;}public boolean isConnection(int p,int q){int parentP=find(p);int parentQ=find(q);return parentP==parentQ;}public int find(int x){if(parent[x]!=x){parent[x]=find(parent[x]);//路径压缩}return parent[x];}public int getCount(){int cnt=0;//找0所在的集合int rt=find(0);for(int i=0;i<parent.length;i++){if(rt==find(i))cnt++;}return cnt;}
}
有任何问题,欢迎评论区交流,欢迎评论区提供其它解题思路(代码),也可以点个赞支持一下作者哈😄~
相关文章:

2024.3.2力扣每日一题——受限条件下可到达节点的数目
2024.3.2 题目来源我的题解方法一 深度优先搜索方法二 并查集 题目来源 力扣每日一题;题序:2368 我的题解 方法一 深度优先搜索 使用深度优先搜索实现,在搜索过程中根据restricted进行截停。 时间复杂度:O(n) 空间复杂度&#…...
在云端遇见雨云:一位服务器寻觅者的指南
引言:寻觅一座云端归宿 当我踏入数字世界的边缘,带着对网络的探索与期待,我迫切需要一座安全可靠的数字栖息地。云计算技术正如一场魔法般的变革,而在这片广袤的云端中,雨云就像是一位友善的向导,引领我穿越…...
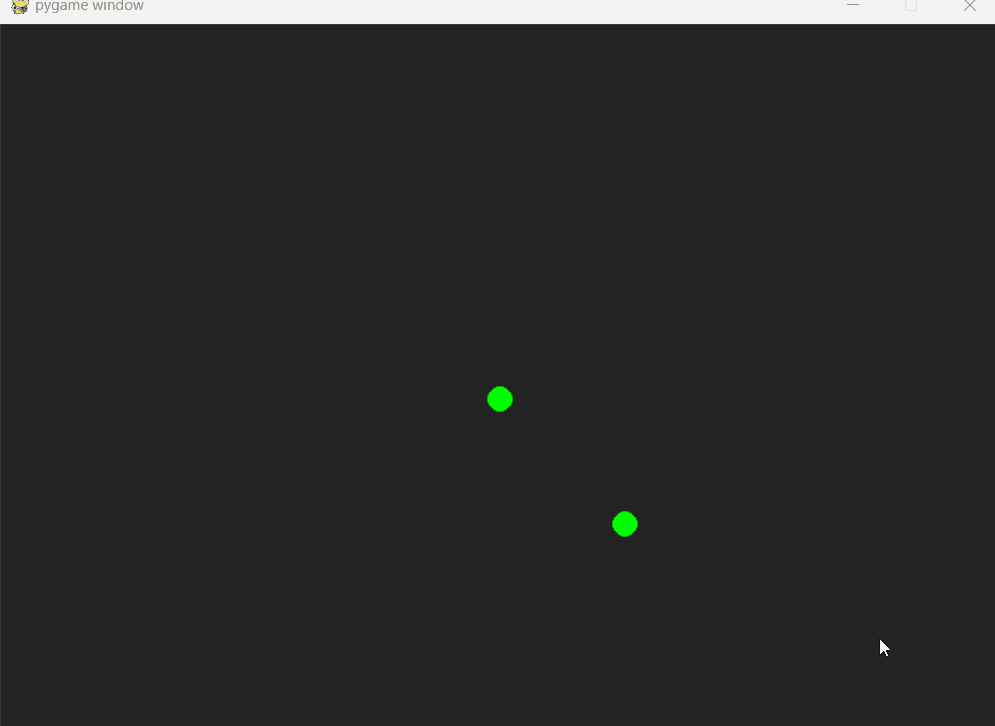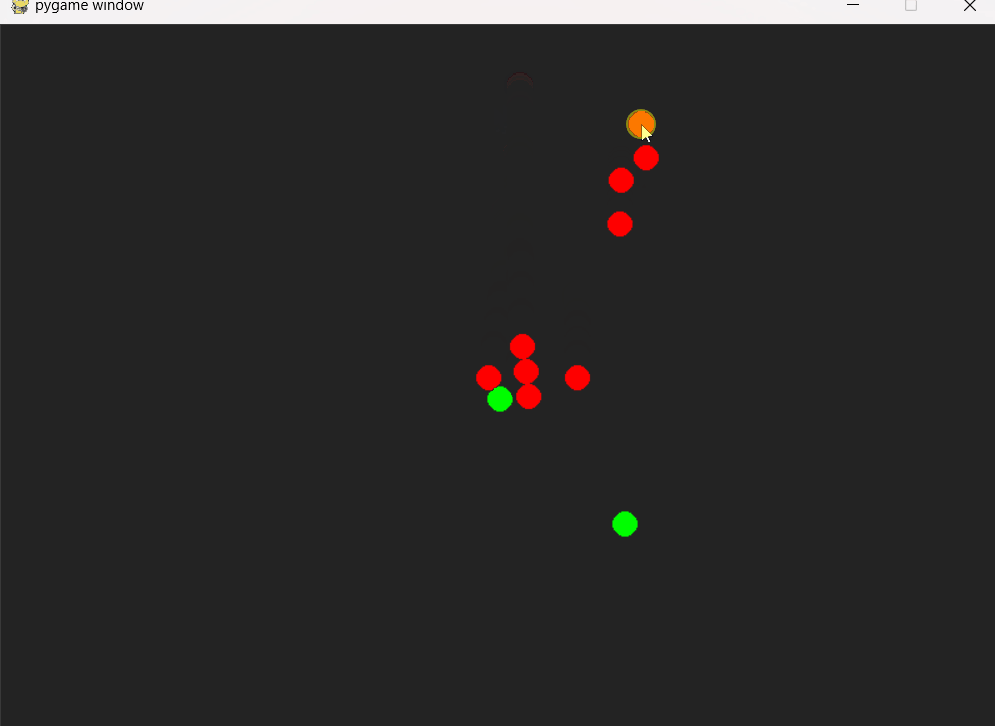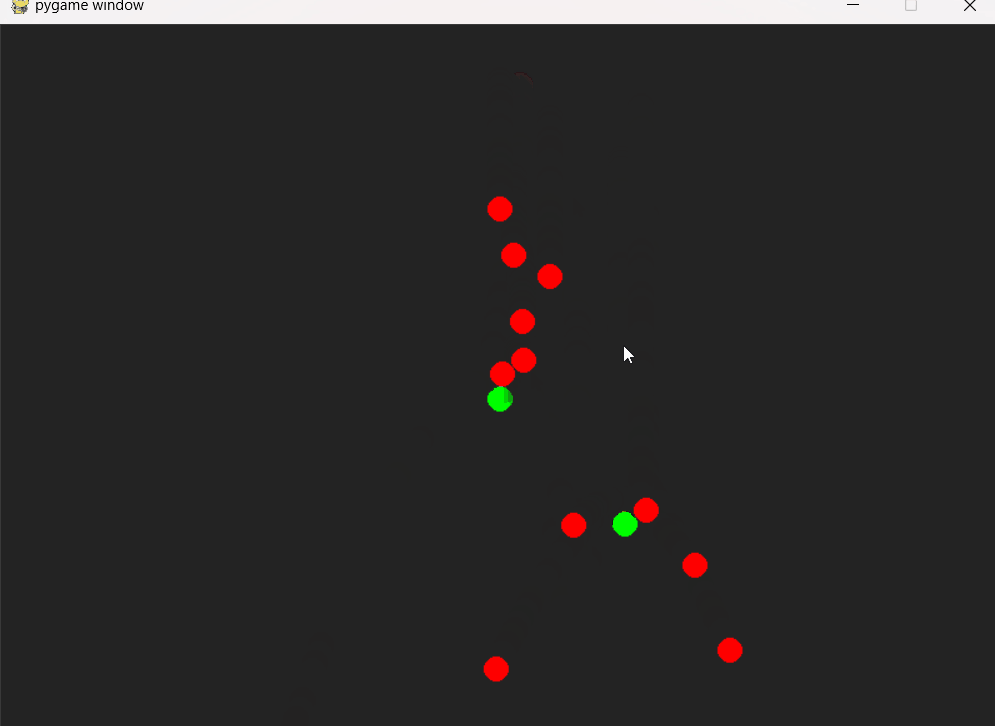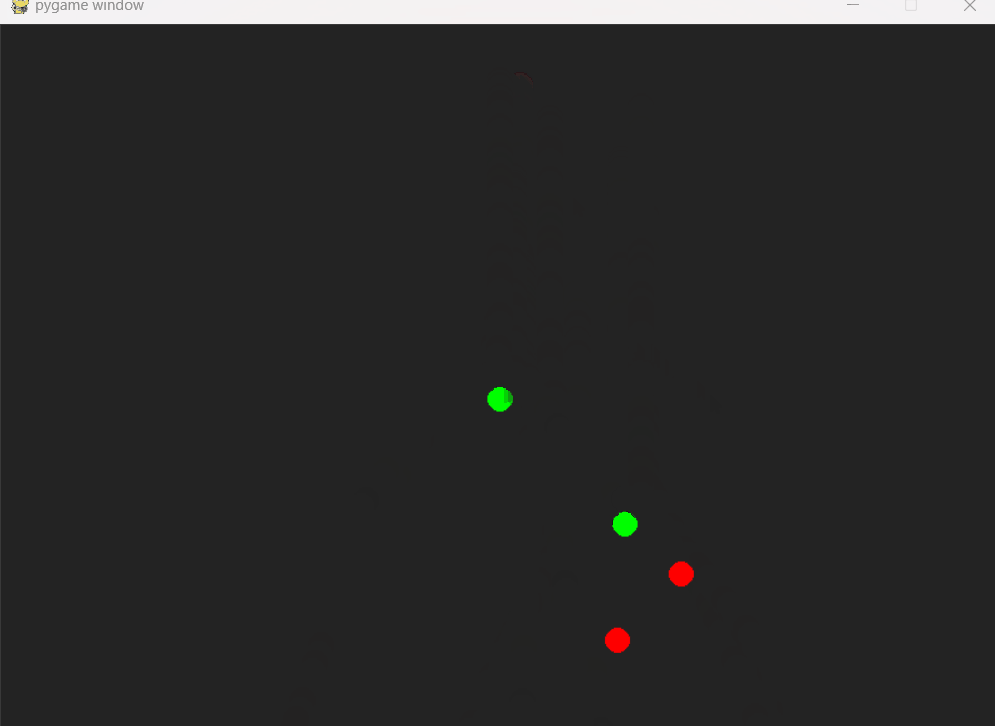
Pygame基础10-物理模拟
PyMunk PyMunk是一个模拟物理的库。 注意,PyMunk只是进行物理模拟,不包含可视化的功能。如果需要可视化,可使用pygame等库。 可用pip安装pymunk pip install pymunk pymunk中的概念: space: 物理空间。 包含gravity 模…...

蓝桥杯 --- 日期问题模板
目录 1.如何判断闰年 2.如何遍历当前年份的每一天 3.如果想要输出某一年某一天到某一年某一天之间一共有多少天。 4.精确到具体周几到周几的问题分析 5.如何直接通过一层for循环枚举年月日 习题: 蓝桥杯竞赛特别喜欢考日期问题,今天给大家分享一下…...

Java 处理Mysql获取树形的数据
Mysql数据: 代码如下: Entity: Data Accessors(chain true) public class Region {private BigInteger id;//名称private String name;//父idprivate BigInteger parentId;private List<Region> children;private Integer createTim…...

前端三剑客 —— CSS ( 坐标问题 、定位问题和图片居中 )
前期内容回顾: 1.常见样式 text-shadow x轴 y轴 阴影的模糊程度 阴影的颜色 box-shadow border-radio 实现圆角 margin 内边距 padding 外边距 background 2.特殊样式 媒体查询:media 自定义字体:font-face { font-family:自定义名称&#…...

向量数据库 | AI时代的航道灯塔
向量数据库 | AI时代的航道灯塔 什么是向量检索服务拍照搜商品 你使用过向量数据库吗?使用体验?为什么向量数据库能借由大模型引起众多关注向量数据库在当前AI热潮中是昙花一现,还是未来AI时代的航道灯塔? 今天的话题主要是讨论向…...

Linux中的conntrack命令深入解析
在Linux网络管理和监控领域,conntrack命令是一个强大的工具,它提供了对netfilter连接跟踪系统的直接访问🔍。这篇文章将深入探讨conntrack的由来、底层原理、参数意义,以及其常见用法,并对返回结果的每个字段进行详细解…...
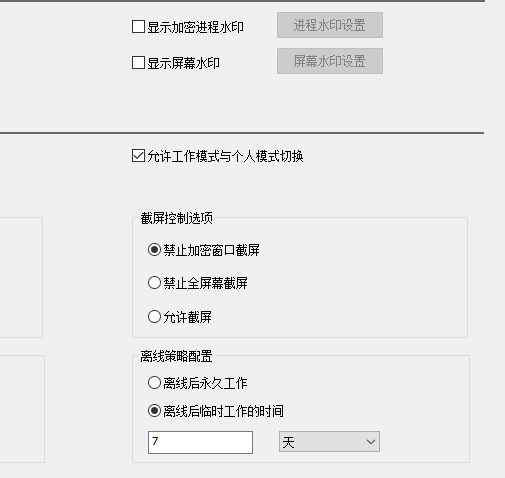
反截屏控制技术如何防止信息通过手机拍照泄漏?
反截屏控制技术为企业数据安全提供了重要的防护措施。通过以下几点,有效阻止了信息通过拍照等方式的泄漏: 反截屏控制开启,用户启动截屏操作时,允许非涉密内容截屏操作,但所有涉密内容窗口会自动隐藏,防止涉…...

0.k8s简介
目录 k8s是什么 k8s不是什么 云原生 微服务 整体式架构与微服务架构 微服务的特性 微服务的优势 k8s是什么 Kubernetes 是一个可移植、可扩展的开源平台,用于管理容器化的工作负载和服务,可促进声明式配置和自动化。 Kubernetes 拥有一个庞大且快…...
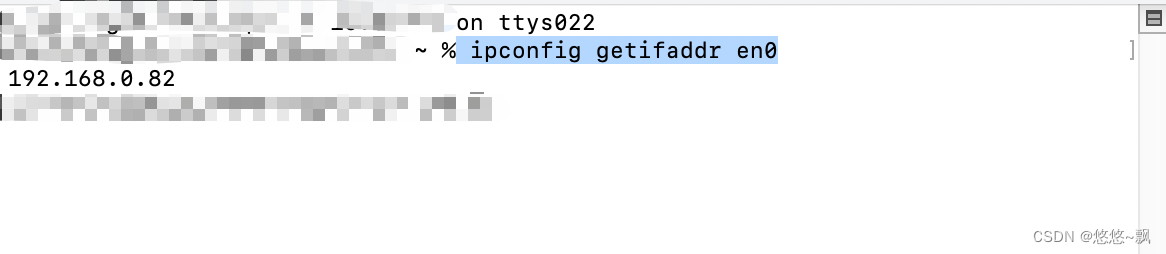
VScode 集成终端设置默认打开当前文件夹 mac系统
一.快捷键设置 搜索 openInIntegratedTerminal 如图: 二.设置cmd 默认打开位置 点击设置 搜索 ntegrated:cwd 如下图: 三.查看ip 快捷指令: ipconfig getifaddr en0...
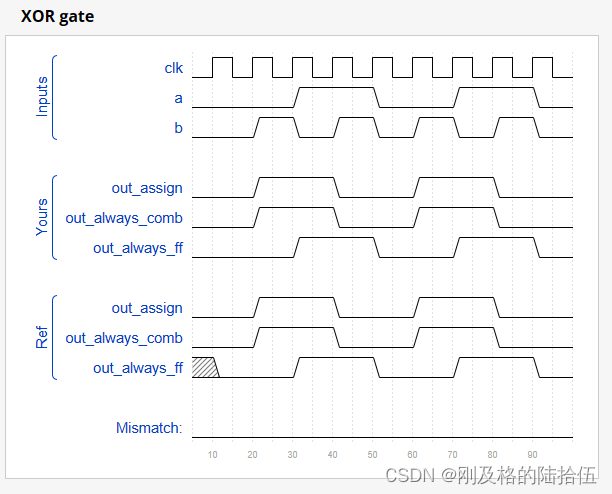
HDLbits 刷题 -- Alwaysblock2
学习: For hardware synthesis, there are two types of always blocks that are relevant: Combinational: always (*)Clocked: always (posedge clk) Clocked always blocks create a blob of combinational logic just like combinational always blocks, but…...
一、Docker部署GitLab(详细步骤)
Docker部署GitLab(详细步骤) 一、拉取镜像二、启动容器三、修改配置四、修改密码五、浏览器访问 一、拉取镜像 docker安装教程:https://qingsi.blog.csdn.net/article/details/131270071 docker pull gitlab/gitlab-ce:latest二、启动容器 …...
)
Vue3 Ajax(axios)
Vue 版本推荐使用 axios 来完成 ajax 请求。 安装方法 使用 cdn: <script src"https://unpkg.com/axios/dist/axios.min.js"></script> 使用 npm: $ npm install axios GET 方法 我们可以简单的读取 JSON 数据: const app {data() {r…...
正则表达式引擎库汇合
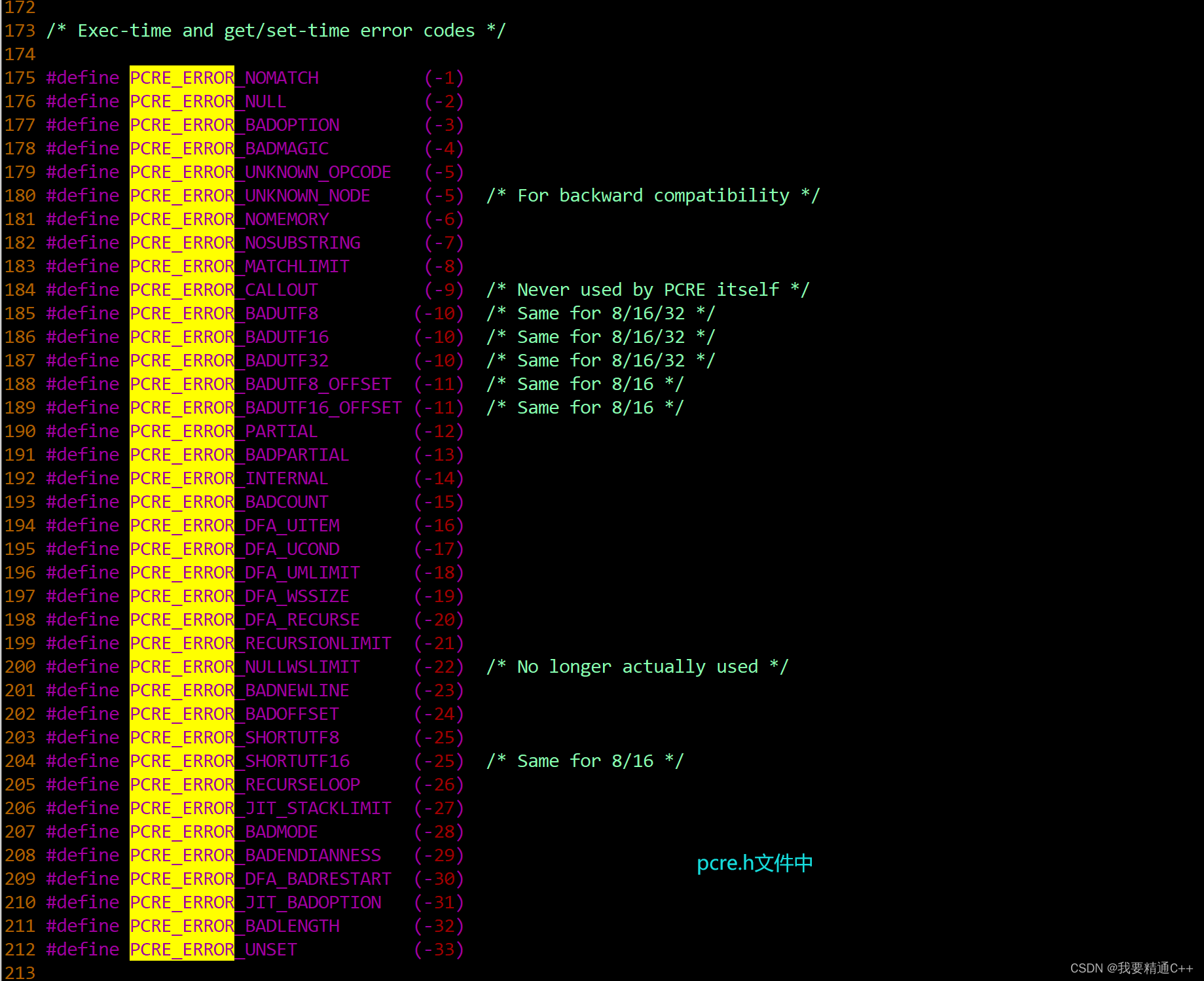
1.总览表格 一些正则表达式库的对比 index库名编程语言说明代码示例编译指令1Posix正则C语言是C标准库中用于编译POSIX风格的正则表达式库 posix-re.cgcc posix-re.c 2PCRE库C语言提供类似Perl语言的一个正则表达式引擎库。 一般系统上对应/usr/lib64/libpcre.so这个库文件&am…...

eBay买家号注册下单容易死号?是什么原因导致?
随着电子商务的迅猛发展,跨境电商平台eBay日益成为众多消费者和商家的首选。然而,自去年下半年以来,eBay推出的新规则给买家号的注册带来了前所未有的挑战。许多新用户反映,在注册eBay买家号后,往往遭遇刚注册就被冻结…...
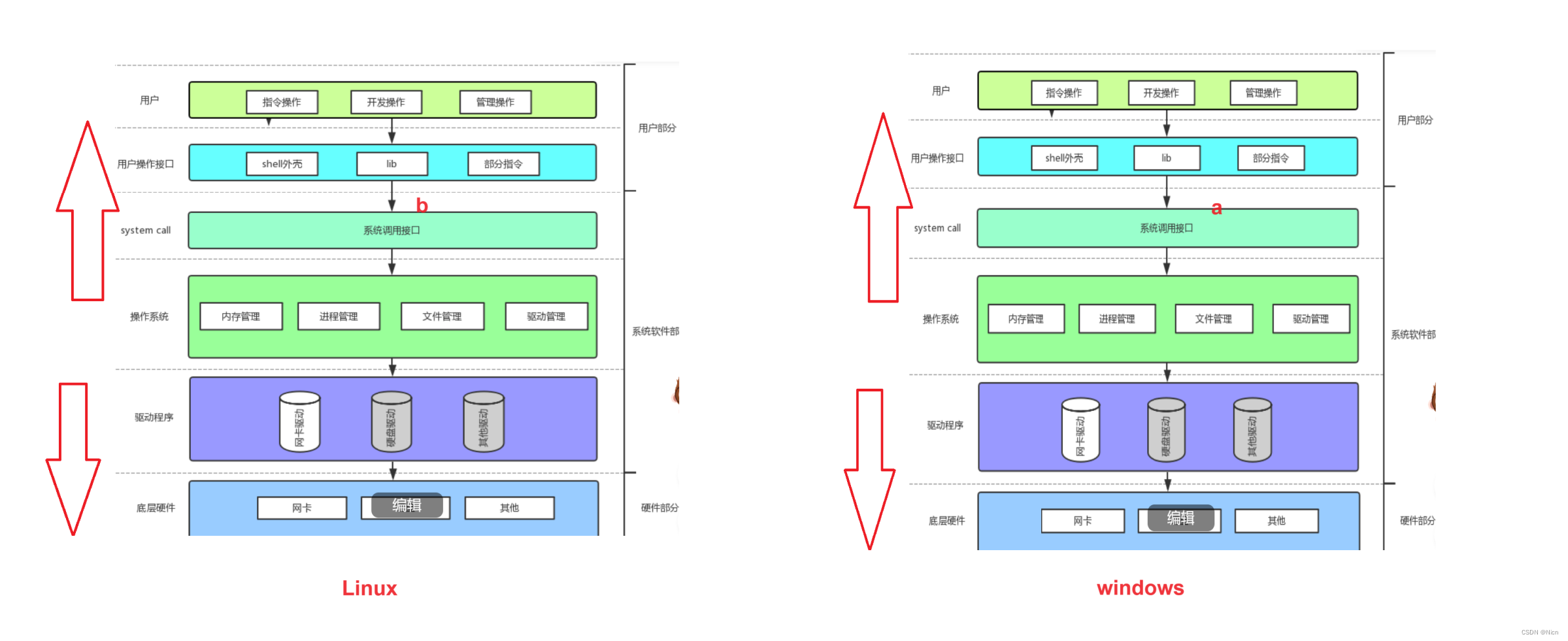
【Linux】-进程知识铺垫①计算机硬件的组织:冯诺依曼体系结构详细解读②关于操作系统对软硬件及用户的意义
目录 编辑 1.关于计算机的体系结构 1.1 冯诺依曼体系结构的诞生 2.冯诺依曼体系结构 2.1 cpu:运算器:更多的是让cpu具有特殊的数据计算功能: 2.2 控制器 2.3输入设备 2.4输出设备 3.计算机各个硬件设备之间的关系 4.内存与计算机效率 5.关于为什么总说…...

让ECC升级S/4HANA一步到位的“全面升级方案包”
SAP最新一代商务套件S/4HANA比ECC系统拥有更高性能的存储数据库HANA、更个性化的Fiori用户界面设计系统,能够大大提升系统效率,带来便捷、高效、良好的用户体验。但企业原先使用的ECC系统里面保存了积累多年的关键流程和数据,让企业面对系统升…...

AutoGluon
官网 amazon (base) PS C:\Users\gg葱> conda env list # conda environments: # pytorch1 C:\Users\gg葱\.conda\envs\pytorch1 base * D:\ANCDD:\Documents\LMm\env\pytorch2(base) PS C:\Users\gg葱> conda create --prefixD:/Doc…...
【网站项目】少儿编程管理系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...
