Linux线程概念
重新认识一下进程
在之前写过的与进程相关的博文中,都把进程看作是只有一个PCB的进程。如图:
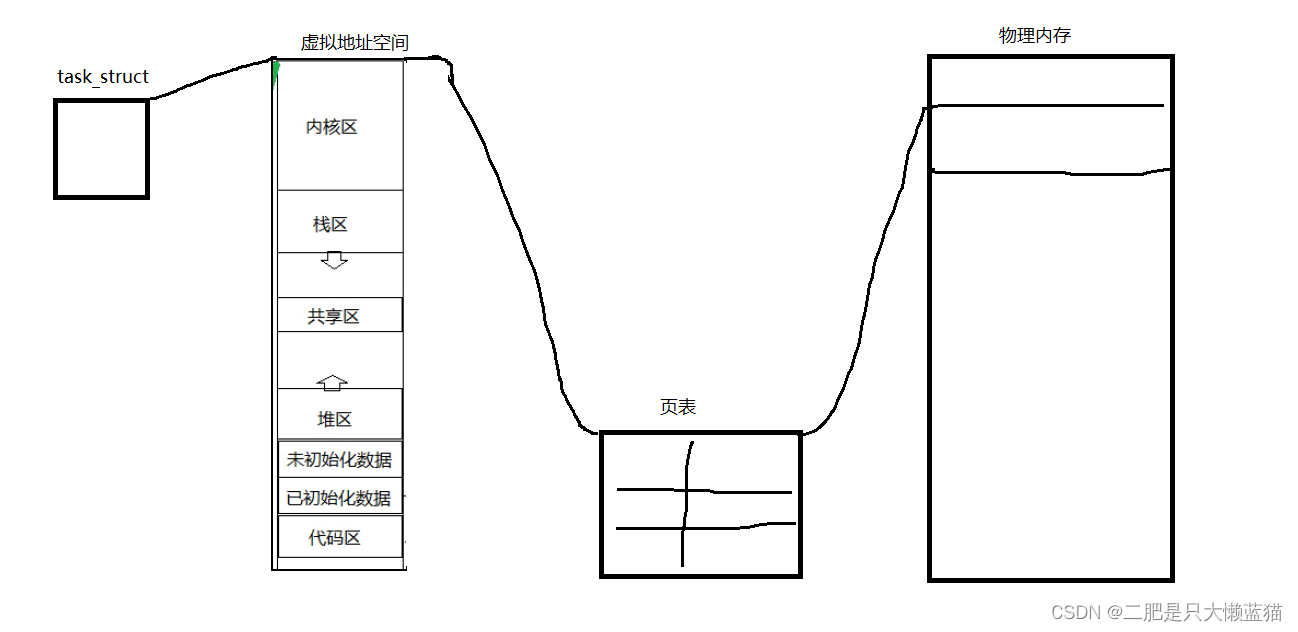
而实际上,在Linux中,进程不止一个执行流,而是可能会有几个或很多个。同一个进程中,每一个执行流都指向同一个虚拟地址空间,由操作系统创建。即在完整的进程中,进程包括:若干个执行流,虚拟地址空间,页表,以及存在物理内存中属于该进程的数据和代码。
我们透过进程虚拟地址空间,可以看到进程的大部分资源,将进程资源合理分配给每个执行流。当CPU调度进程的时候,只看执行流PCB。
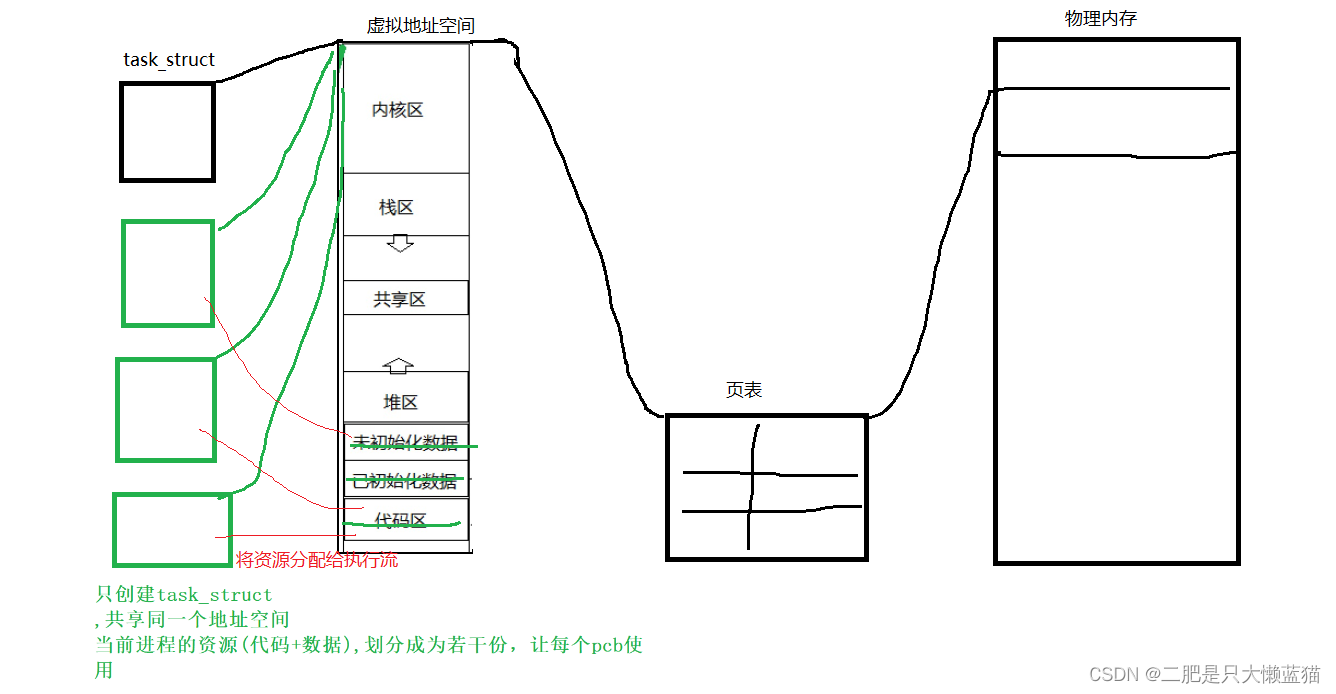
通过上述对进程的重新认识,我们可以知道了一个进程内可以有1个执行流,也可以有多个。
线程的概念
首先我们得知道一件事:在Linux中,没有专门为线程设计的TCB,而是使用进程的PCB来模拟线程。
在教科书上面,对线程的概念是:在进程内部运行的一个执行流,属于进程的一部分,粒度要比进程更加细和轻量化。
我们可以对这句话进行解析:在进程内部运行,即线程在地址空间中运行。所谓执行流,即对于CPU来说,它只看PCB,而在进程中的每一个PCB都被分配了若干资源,CPU可以直接调度它们,按照一定的序列去调度。
因此,我们可以理解线程是"一个进程内部的控制序列"。
了解了什么是线程后,我们来看看在Linux中进程和线程的关系。
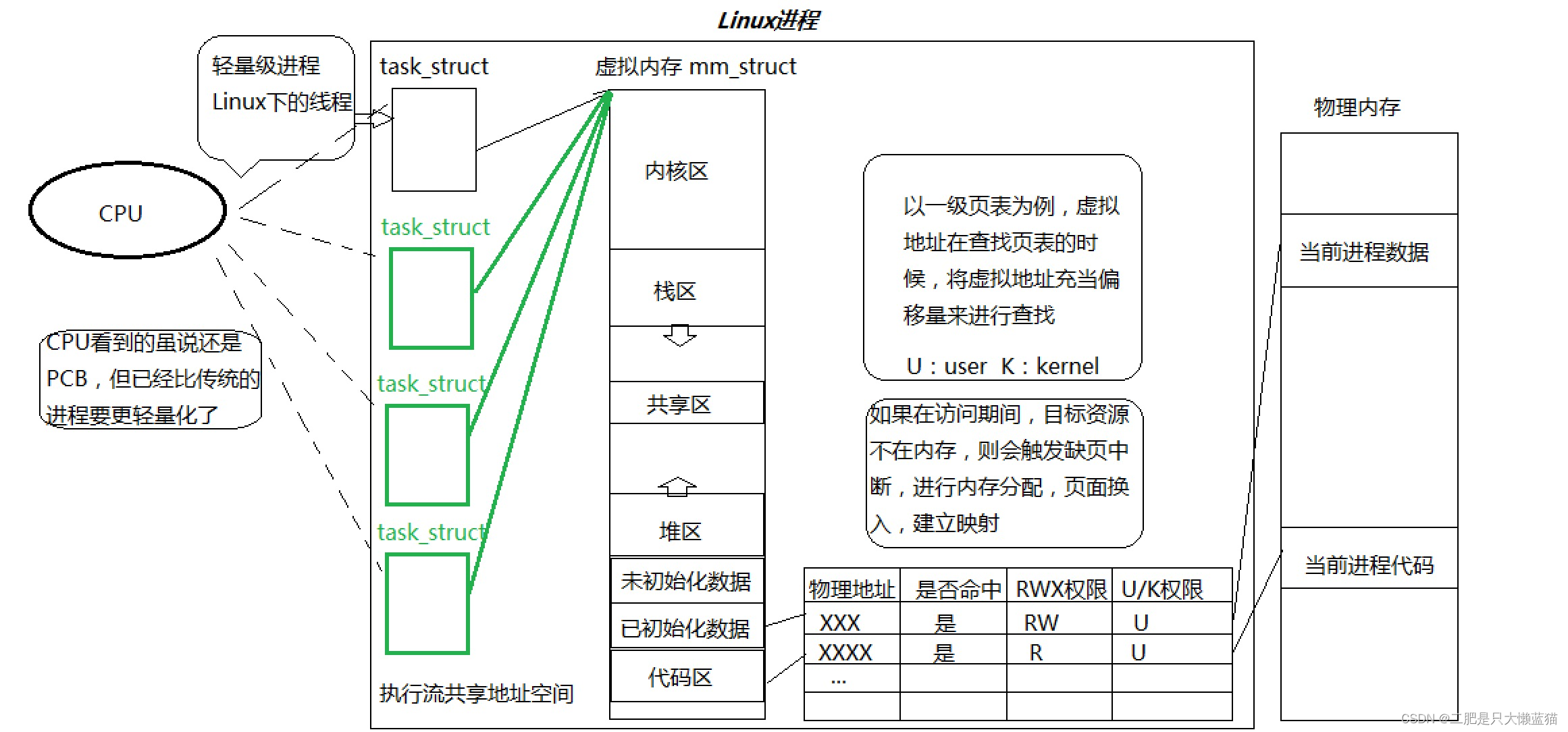
进程和线程
因为Linux中的线程是进程的PCB模拟出来的,因此不用维护线程和进程的复杂关系,不用单独为线程设计任何算法,而是直接使用进程的的一套相关的方法即可。OS只需聚焦在线程的资源分配上就可以了。
从内核视角看进程和线程的关系:
进程是承担分配系统资源的基本实体。线程是CPU调度的基本单位,承担进程资源的一部分的基本实体。也就是说,线程是向进程要资源,进程向OS要资源,CPU调度进程中的执行流,即线程。
看待Linux线程和接口:
Linux进程是轻量级的进程,在进程中,OS创建线程,CPU调度线程。Linux没有给一般用户提供直接操作线程的接口,而是提供了在同一个地址空间内创建PCB的方法和分配资源给指定PCB的接口。
进程和线程的共享和私有:
其实在Linux中没有线程这个东西,我的意思是没有真正独特设计出来的线程。因此在Linux中,所谓的线程,是轻量级的进程。所有的轻量级进程(可能是“线程”)都是在进程内部运行的(地址空间)。
对于进程,它大部分是具有独立性的,而有部分是共享资源(管道,ipc资源)。
对于线程,大部分资源都是共享的,有部分资源是“私有”的(线程ID、一组寄存器、栈、errno、信号屏蔽字、调度优先级等等)。
进程的多个线程共享 同一地址空间,因此Text Segment、Data Segment都是共享的,如果定义一个函数,在各线程中都可以调用,如果定义一个全局变量,在各线程中都可以访问到,除此之外,各线程还共享以下进程资源和环境:文件描述符表、每种信号的处理方式(SIG_ IGN、SIG_ DFL或者自定义的信号处理函数)、当前工作目录、用户id和组id。
线程的优点:
①创建一个新线程的代价要比创建一个新进程小得多
②与进程之间的切换相比,线程之间的切换需要操作系统做的工作要少很多
③线程占用的资源要比进程少很多
④能充分利用多处理器的可并行数量
⑤在等待慢速I/O操作结束的同时,程序可执行其他的计算任务
⑥计算密集型应用,为了能在多处理器系统上运行,将计算分解到多个线程中实现
⑦I/O密集型应用,为了提高性能,将I/O操作重叠。线程可以同时等待不同的I/O操作
线程的缺点:
①性能损失:一个很少被外部事件阻塞的计算密集型线程往往无法与共它线程共享同一个处理器。如果计算密集型线程的数量比可用的处理器多,那么可能会有较大的性能损失,这里的性能损失指的是增加了额外的同步和调度开销,而可用的资源不变。
②健壮性降低:编写多线程需要更全面更深入的考虑,在一个多线程程序里,因时间分配上的细微偏差或者因共享了不该共享的变量而造成不良影响的可能性是很大的,换句话说线程之间是缺乏保护的。
③缺乏访问控制:进程是访问控制的基本粒度,在一个线程中调用某些OS函数会对整个进程造成影响。
④编程难度提高:编写与调试一个多线程程序比单线程程序困难得多
线程异常:
①单个线程如果出现除零,野指针问题导致线程崩溃,进程也会随着崩溃
②线程是进程的执行分支,线程出异常,就类似进程出异常,进而触发信号机制,终止进程,进程终止,该进程内的所有线程也就随即退出
合理的使用多线程,能提高CPU密集型程序的执行效率,能提高IO密集型程序的用户体验(如生活中我们一边写代码一边下载开发工具,就是多线程运行的一种表现)。
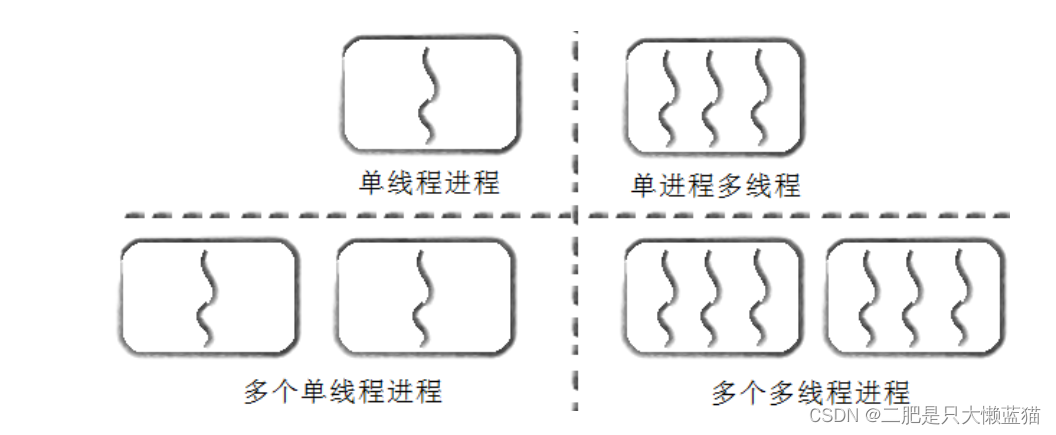
Linux下线程和进程的关系图:
可以看到,线程是进程的每一个执行流,一个进程中可以包含多个线程,也可以只有一个线程。
相关文章:

Linux线程概念
重新认识一下进程 在之前写过的与进程相关的博文中,都把进程看作是只有一个PCB的进程。如图: 而实际上,在Linux中,进程不止一个执行流,而是可能会有几个或很多个。同一个进程中,每一个执行流都指向同一个虚…...

C#基础教程10 方法
C#方法 方法的语法访问修饰符:返回类型:方法名称:参数列表:方法体:返回值:方法的调用参数传递按值传递按引用传递输出参数方法的重载总结方法是C#中最基本的代码结构之一。方法是一组可重复使用的代码,它接受输入,执行一些操作并返回结果。在本教程中,我们将深入了解C…...
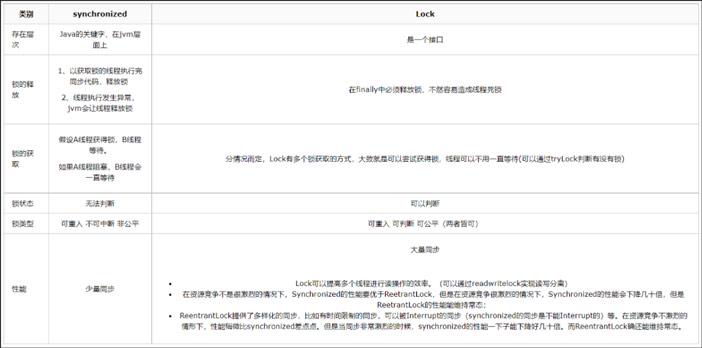
java高性能并发计数器之巅峰对决
并发计数器各个方案介绍方案概述1. jdk5提供的原子更新长整型类 AtomicLong2. synchronized3. jdk8提供的 LongAdder 【单机推荐】4. Redisson分布式累加器【分布式推荐】方案介绍jdk5提供的原子更新长整型类 AtomicLong在JDK1.5开始就新增了并发的Integer/Long的操作工具类Ato…...

HTTPS简介
HTTPS是HTTP开启TLS传输协议,客户端要拿到服务端的公钥,用公钥加密数据后再进行传输,防止数据泄露后背篡改。它要解决两个问题:怎么保证公钥可信怎么加密数据公钥可信问题客户端从服务端获取公钥的时候,存在请求被拦截…...

K-means聚类
原理说明 Kmeans是一种常见的聚类算法,用于将相似的数据点归类到不同的群组中。Kmeans的原理如下: 初始化:Kmeans算法首先需要初始化一个用户指定数量的聚类中心点,通常是随机选取K个数据点作为聚类中心点。 分配:对…...

04-SQL基础(表管理,约束,多表连接,子查询)
本文章主要内容 1、表的管理:创建表,修改表结构,删除字段,修改字段,添加字段,删除表,添加表约束; 2、数据管理:新增记录,修改记录,删除记录&…...
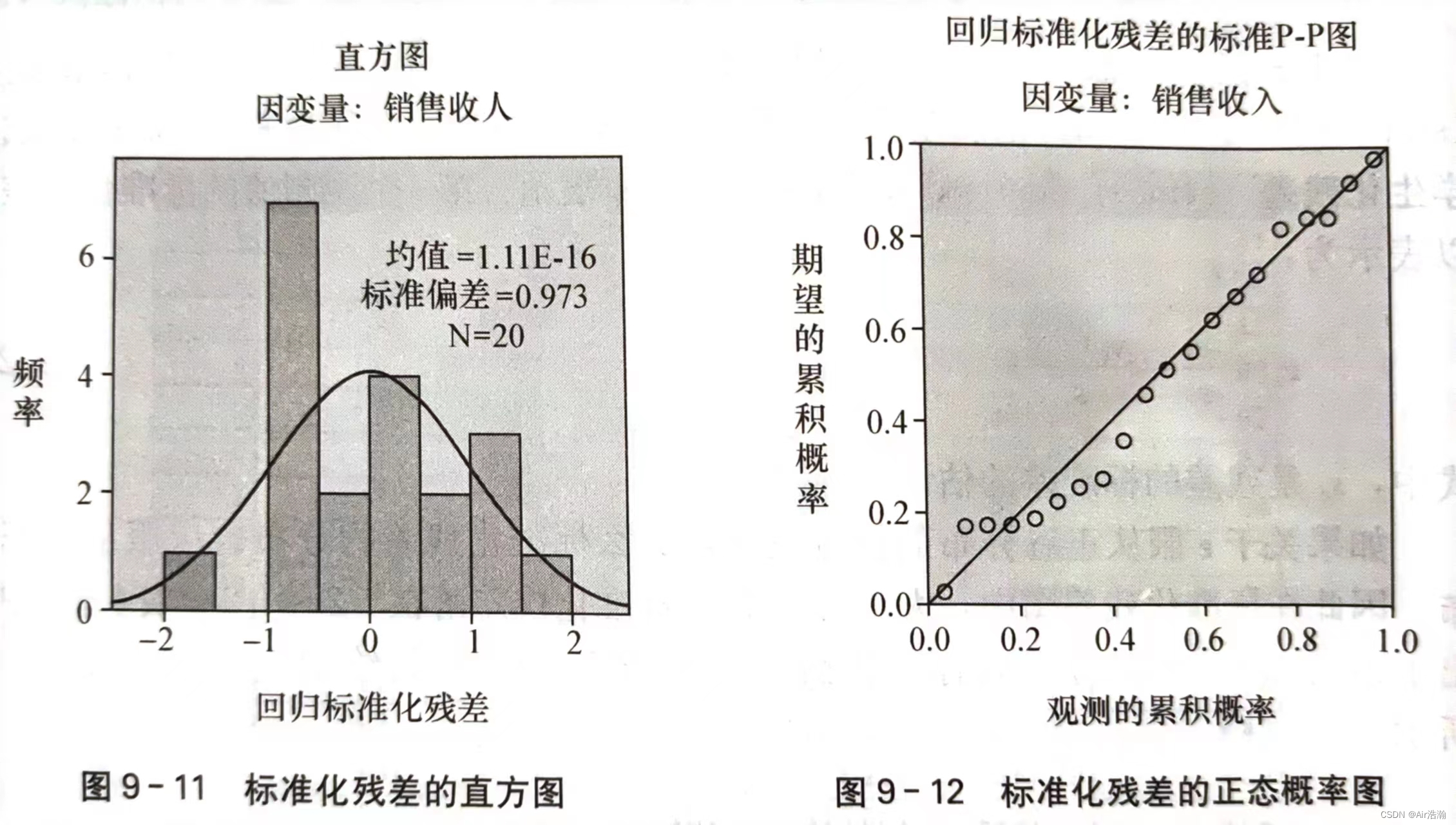
统计学 一元线性回归
统计学 一元线性回归 回归(Regression):假定因变量与自变量之间有某种关系,并把这种关系用适当的数学模型表达出来,利用该模型根据给定的自变量来预测因变量 线性回归:因变量和自变量之间是线性关系 非线…...

【软件开发】基于PyQt5开发的标注软件
这里是基于PyQt5写的面向目标检测的各类标注PC端软件系统。目前现有的labelme软件和labelImg开源软件无法满足特殊数据集的标注要求,而且没有标注顺序的报错提示。当然我设计的软件就会不具有适用性了(毕竟从下面开发的软件可以明显看出来我做的基本上是…...

CSS3新特性
CSS3新特性前言css3选择器边框特性背景参考前言 css3作为css的升级版本,css3提供了更加丰富实用的规范。新特性有: css3选择器边框特性多背景图颜色与透明度多列布局与弹性盒模型布局盒子的变形过渡与动画web字体媒体查询阴影 css3选择器 css3选择器…...

35 openEuler搭建repo(yum)服务器-创建、更新本地repo源
文章目录35 openEuler搭建repo(yum)服务器-创建、更新本地repo源35.1 获取ISO发布包35.2 挂载ISO创建repo源35.3 创建本地repo源35.4 更新repo源35 openEuler搭建repo(yum)服务器-创建、更新本地repo源 使用mount挂载,…...
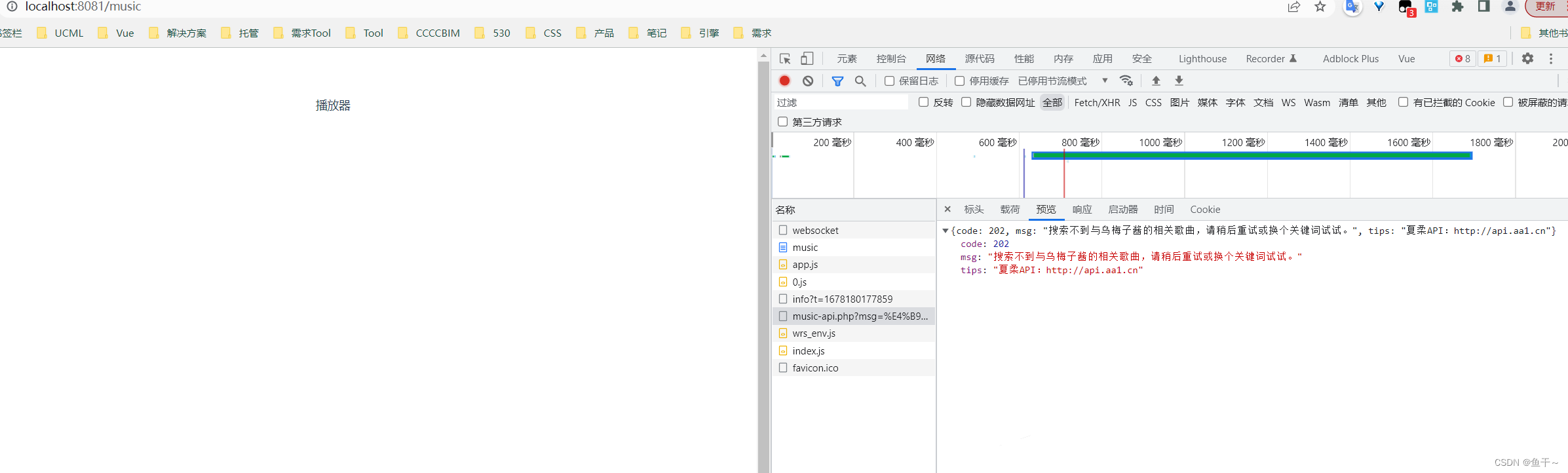
【三.项目引入axios、申明全局变量、设置跨域】
根据前文《二.项目使用vue-router,引入ant-design-vue的UI框架,引入less》搭建好脚手架后使用 需求: 1.项目引入axios 2.申明全局变量 3.设置跨域 简介:axios本质上还是对原生XMLHttpRequest的封装,可用于浏览器和nodejs的HTTP客…...

启动u盘还原成普通u盘(Windows Diskpart)
使用windows系统的diskpart 命令解决系统盘恢复成普通U盘的问题:1. 按Windows R键打开运行窗口。在搜索框中输入“ Diskpart ”,然后按 Enter 键。2. 现在输入“ list disk ”并回车。3. 然后输入“ select disk X ”(将 X 替换为可启动U盘的…...
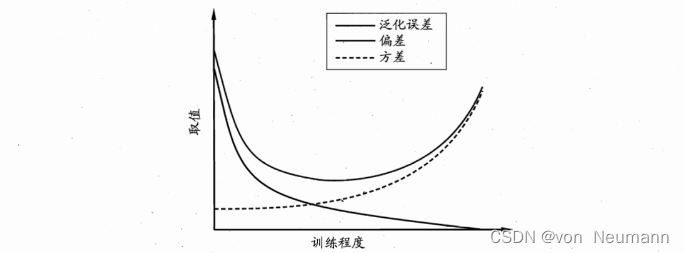
深入理解机器学习——偏差(Bias)与方差(Variance)
分类目录:《深入理解机器学习》总目录 偏差(Bias)与方差(Variance)是解释学习算法泛化性能的一种重要工具。偏差方差分解试图对学习算法的期望泛化错误率进行拆解,我们知道,算法在不同训练集上学…...

分布式新闻项目实战 - 13.项目部署_持续集成(Jenkins) ^_^ 完结啦 ~
欲买桂花同载酒,终不似,少年游。 系列文章目录 项目搭建App登录及网关App文章自媒体平台(博主后台)自媒体文章审核延迟任务kafka及文章上下架App端文章搜索后台系统管理Long类型精度丢失问题定时计算热点文章(xxl-Job…...

Linux c/c++技术方向分析
一、C与C介绍 1.1 说明 c语言是一门面向过程的、抽象化的通用程序设计语言,广泛应用于底层开发,如嵌入式。C语言能以简易的方式编译、处理低级存储器。是一种高效率程序设计语言。 c(c plus plus)是一种计算机高级程序设计语言&a…...
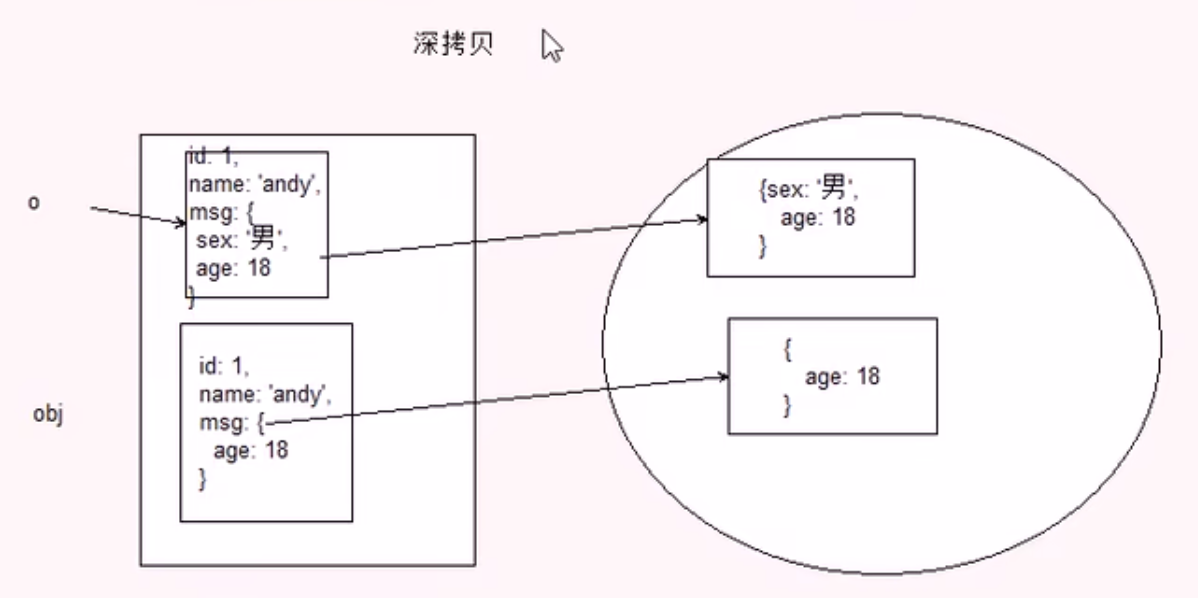
JavaScript 高级3 :函数进阶
JavaScript 高级3 :函数进阶 Date: January 19, 2023 Text: 函数的定义和调用、this、严格模式、高阶函数、闭包、递归 目标: 能够说出函数的多种定义和调用方式 能够说出和改变函数内部 this 的指向 能够说出严格模式的特点 能够把函数作为参数和返…...
【项目】Java树形结构集合分页,java对list集合进行分页
Java树形结构集合分页需求难点实现第一步:查出所有树形集合数据 (需进行缓存处理)selectTree 方法步骤:TreeUtil类:第二步:分页 GoodsCategoryController分页getGoodsCategoryTree方法步骤:第三…...
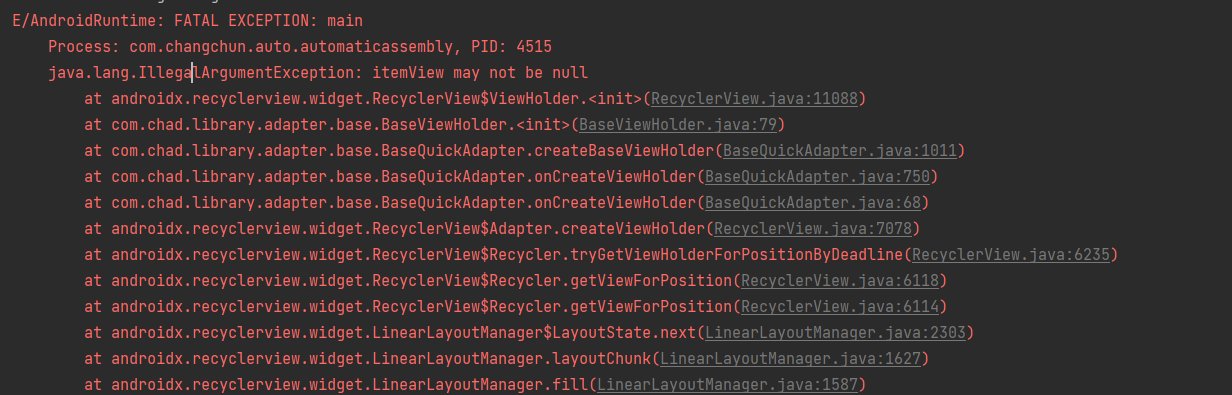
java.lang.IllegalArgumentException: itemView may not be null
报错截图:场景介绍:在使用recycleView 自动递增数据,且自动滚动到最新行; 当数据达到273条 时出现ANR;项目中 全部的列表适配器使用的三方库:BaseRecyclerViewAdapterHelper (很早之前的项目&am…...
[ 攻防演练演示篇 ] 利用 shiro 反序列化漏洞获取主机权限
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

达人合作加持品牌布局,3.8女神玩转流量策略!
随着迅猛发展的“她经济”,使社区本就作为内容种草的平台,自带“营销基因”。在3.8女神节即将到来之际,如何充分利用平台女性资源优势,借助达人合作等手段,实现迅速引流,来为大家详细解读下。一、小红书节日…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...
