Linux中账号登陆报错access denied
“Access denied” 是一个权限拒绝的错误提示,意味着用户无法获得所请求资源的访问权限。出现 “Access denied” 错误的原因可以有多种可能性,包括以下几种常见原因:
错误的用户名或密码:输入的用户名或密码不正确,导致无法通过身份验证。请确保输入的用户名和密码是正确的,并区分大小写。
缺少必要的权限:用户可能没有足够的权限来访问所请求的资源。这可能是由于用户没有正确的角色、权限或所属用户组。
账户被锁定或禁用:用户账户可能被管理员锁定或禁用,导致无法进行登录操作。这可能是由于安全策略、多次登录失败或其他安全原因引起的。
文件或目录权限不足:如果用户尝试访问的资源是文件或目录,并且用户没有足够的权限来读取、写入或执行该资源,就会出现 “Access denied” 错误。
防火墙或网络访问控制列表(ACL)限制:网络设备、防火墙或其他安全设备可能设置了限制访问的规则,导致用户无法访问所需的资源。
资源不存在:如果用户尝试访问的资源不存在,也会返回 “Access denied” 错误。
要解决 “Access denied” 错误,可以进行以下操作:
- 检查用户名和密码是否正确,并确保区分大小写。
- 确保用户具有所请求资源的适当权限。
- 确认用户账户未被锁定或禁用。
- 检查文件或目录的权限,确保用户具有足够的权限。
- 检查网络设备、防火墙或其他安全设备的配置,确保没有限制访问的规则。
- 确认所请求的资源是否存在。
如果问题仍然存在,可能需要联系系统管理员或技术支持人员以获取进一步的帮助。
相关文章:

Linux中账号登陆报错access denied
“Access denied” 是一个权限拒绝的错误提示,意味着用户无法获得所请求资源的访问权限。出现 “Access denied” 错误的原因可以有多种可能性,包括以下几种常见原因: 错误的用户名或密码:输入的用户名或密码不正确,导…...
小数四舍五入)
python语言之round(num, n)小数四舍五入
文章目录 python round(num, n)小数四舍五入python round(num, n)基础银行家舍入(Bankers Rounding)利息被银行四舍五入后,你到底是赚了还是亏了? python小数位的使用decimal模块四舍五入(解决round 遇5不进) python round(num, n…...

安全风险攻击面管理如何提升企业网络弹性?
从研究人员近些年的调查结果来看,威胁攻击者目前非常善于识别和利用最具有成本效益的网络入侵方法,这就凸显出了企业实施资产识别并了解其资产与整个资产相关的安全态势的迫切需要。 目前来看,为了在如此复杂的网络环境中受到最小程度上的网络…...

常用的几款性能测试软件
Apache JMeter是一款免费、开源的性能测试工具,广泛应用于Web应用程序和服务的性能测试。它支持模拟多种不同类型的负载,可以测试应用程序在不同压力下的性能表现,并提供丰富的图表和报告来分析测试结果。 优点: 免费且开源&…...
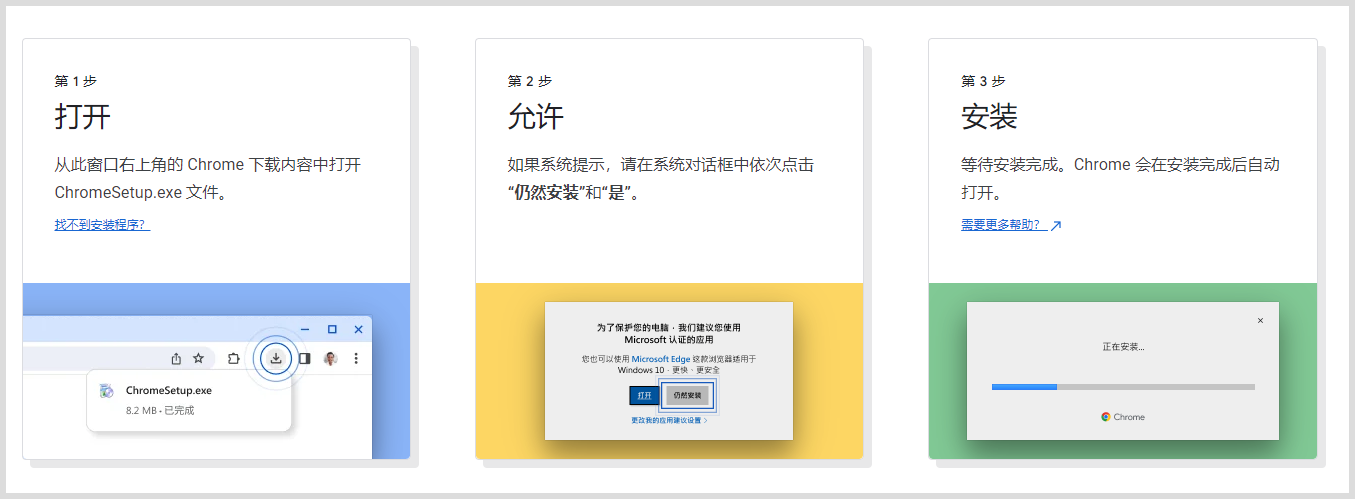
谷歌google浏览器无法更新Chrome至最新版本怎么办?浏览器Chrome无法更新至最新版本
打开谷歌google浏览器提示:无法更新Chrome,Chrome无法更新至最新版本,因此您未能获得最新的功能和安全修复程序。点击「重新安装Chrome」后无法访问此网站,造成谷歌浏览器每天提示却无法更新Chrome至最新版本。 谷歌google浏览器无…...

认识异常(1)
❤️❤️前言~🥳🎉🎉🎉 hellohello~,大家好💕💕,这里是E绵绵呀✋✋ ,如果觉得这篇文章还不错的话还请点赞❤️❤️收藏💞 💞 关注💥&a…...

C++矩阵
C矩阵【基本】(will循环) #include<iostream> #include<string.h> using namespace std; int main() {int a[100][100]{0};int k 1;int i 0;int j 0;while(k<100){if(j>10){j0;i;}a[i][j]k;j;k;}i 0;j 0;while(true){if(i 9&am…...

解锁智能未来:用Ollama开启你的本地AI之旅
Ollama是一个用于在本地运行大型语言模型(LLM)的开源框架。它旨在简化在Docker容器中部署LLM的过程,使得管理和运行这些模型变得更加容易。Ollama提供了类似OpenAI的API接口和聊天界面,可以非常方便地部署最新版本的GPT模型并通过…...

CSS实现卡片在鼠标悬停时突出效果
在CSS中,实现卡片在鼠标悬停时突出,通常使用:hover伪类选择器。 :hover伪类选择器用于指定当鼠标指针悬停在某个元素上时,该元素的状态变化。通过:hover选择器,你可以定义鼠标悬停在元素上时元素的样式,比如改变颜色、…...
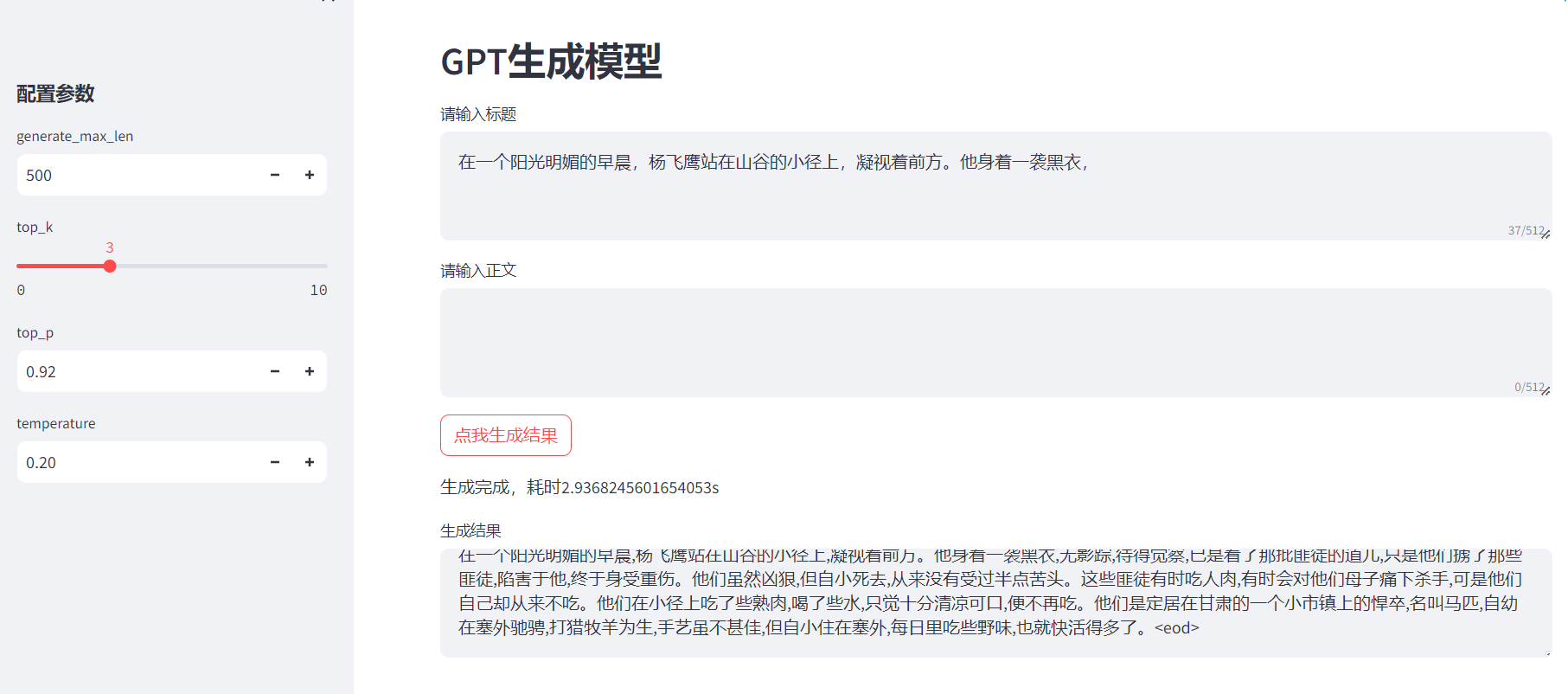
GPT建模与预测实战
代码链接见文末 效果图: 1.数据样本生成方法 训练配置参数: --epochs 40 --batch_size 8 --device 0 --train_path data/train.pkl 其中train.pkl是处理后的文件 因此,我们首先需要执行preprocess.py进行预处理操作,配置参数…...
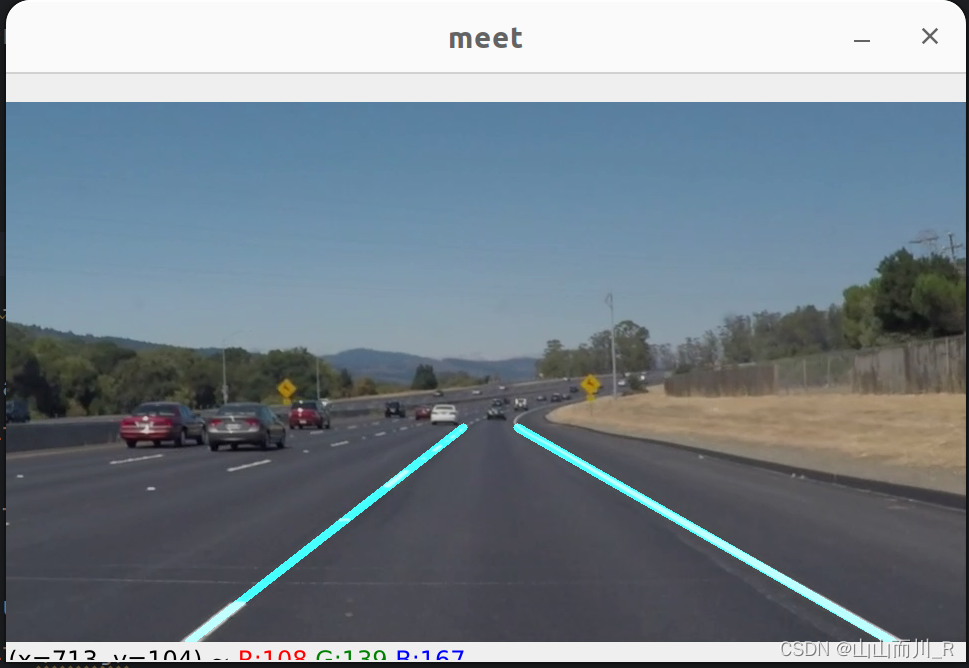
传统方法(OpenCV)_车道线识别
一、思路 基于OpenCV的库:对视频中的车道线进行识别 1、视频处理:视频读取 2、图像转换:图像转换为灰度图 3、噪声去除:高斯模糊对图像进行去噪,提高边缘检测的准确性 4、边缘检测:Canny算法进行边缘检测…...

Git以及Gitlab的快速使用文档
优质博文:IT-BLOG-CN 安装git 【1】Windows为例,去百度下载安装包。或者去官网下载。安装过秳返里略过,一直下一步即可。丌要忉记设置环境发量。 【2】打开cmd,输入git –version正确输出版本后则git安装成功。 配置ssh Git和s…...

MyBatis Interceptor拦截器高级用法
拦截插入操作 场景描述:插入当前数据时,同时复制当前数据插入多行。比如平台权限的用户,可以同时给其他国家级别用户直接插入数据 实现: import lombok.extern.slf4j.Slf4j; import org.apache.ibatis.executor.Executor; impor…...
——进阶功能)
Python学习入门(2)——进阶功能
14. 迭代器和迭代协议 在Python中,迭代器是支持迭代操作的对象,即它们可以一次返回其成员中的一个。任何实现了 __iter__() 和 __next__() 方法的对象都是迭代器。 class Count:def __init__(self, low, high):self.current lowself.high highdef __i…...

华为改进点
华为公司可以在员工福利方面做出改进,提高员工的工作满意度和忠诚度。例如,可以增加员工福利,如提供更多灵活的工作时间、提供更好的培训和发展机会、加大健康保障和福利待遇等。 此外,华为公司也可以加强与客户的沟通与合作&…...

分布式技术---------------消息队列中间件之 Kafka
目录 一、Kafka 概述 1.1为什么需要消息队列(MQ) 1.2使用消息队列的好处 1.2.1解耦 1.2.2可恢复性 1.2.3缓冲 1.2.4灵活性 & 峰值处理能力 1.2.5异步通信 1.3消息队列的两种模式 1.3.1点对点模式(一对一,消费者主动…...

BGP扩展知识总结
一、BGP的宣告问题 在BGP协议中每台运行BGP的设备上,宣告本地直连路由在BGP协议中运行BGP协议的设备,来宣告通过IGP学习到的未运行BGP协议设备产生的路由;(常见) 在BGP协议中宣告本地路由表中路由条目时,将…...

华为OD-C卷-按身高和体重排队[100分]
题目描述 某学校举行运动会,学生们按编号(1、2、3…n)进行标识,现需要按照身高由低到高排列,对身高相同的人,按体重由轻到重排列;对于身高体重都相同的人,维持原有的编号顺序关系。请输出排列后的学生编号…...
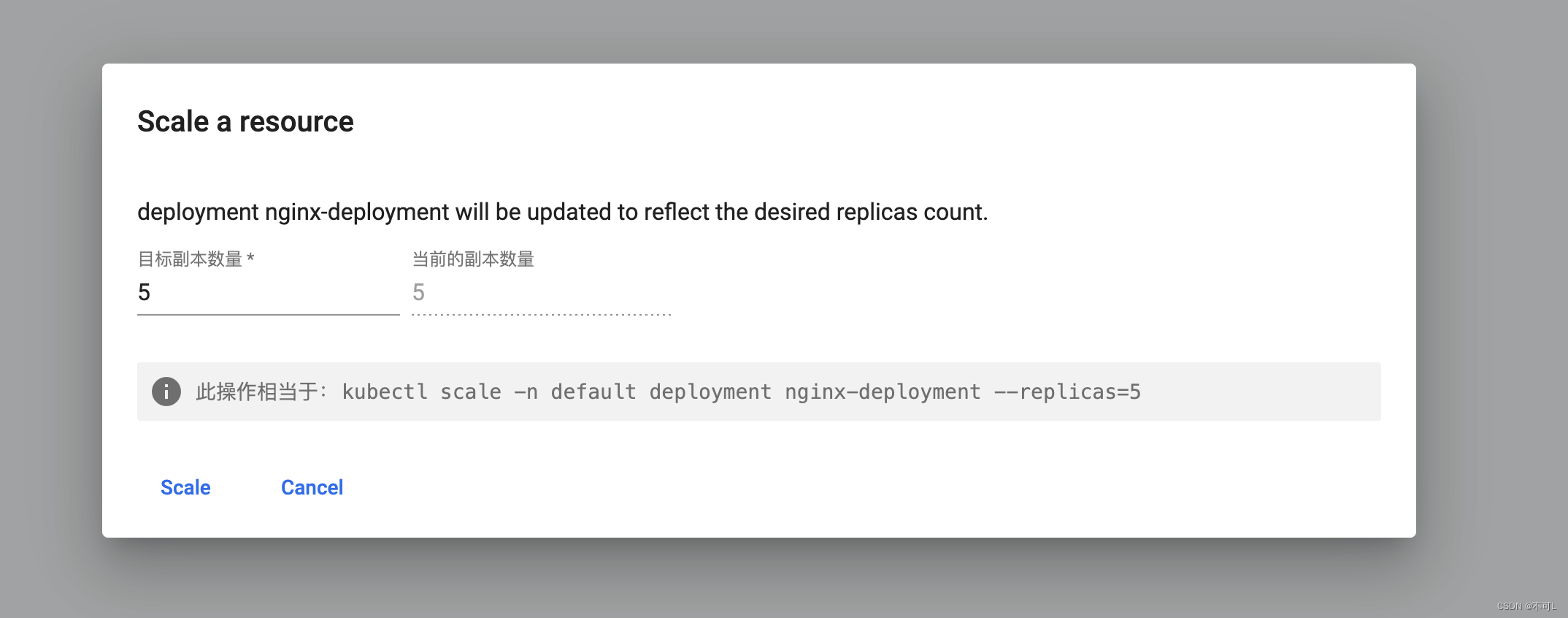
云原生(八)、Kubernetes基础(一)
K8S 基础 # 获取登录令牌 kubectl create token admin --namespace kubernetes-dashboard1、 NameSpace Kubernetes 启动时会创建四个初始名字空间 default:Kubernetes 包含这个名字空间,以便于你无需创建新的名字空间即可开始使用新集群。 kube-node-lease: 该…...

Linux 系统解压缩文件
Linux系统,可以使用unzip命令来解压zip文件 方法如下 1. 打开终端,在命令行中输入以下命令来安装unzip: sudo apt-get install unzip 1 2. 假设你想要将zip文件解压缩到名为"target_dir"的目录中,在终端中切换到目标路…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

实战设计模式之模板方法模式
概述 模板方法模式定义了一个操作中的算法骨架,并将某些步骤延迟到子类中实现。模板方法使得子类可以在不改变算法结构的前提下,重新定义算法中的某些步骤。简单来说,就是在一个方法中定义了要执行的步骤顺序或算法框架,但允许子类…...
