浅述python中NumPy包
NumPy(Numerical Python)是Python的一种开源的数值计算扩展,提供了多维数组对象ndarray,是一个快速、灵活的大数据容器,可以用来存储和处理大型矩阵,支持大量的维度数组与矩阵运算,并针对数组运算提供大量的数学函数库。这些函数可以直接在数组和矩阵上操作,大大简化了数据处理和分析的复杂度。
NumPy数组的元素类型必须相同,具有同质性,以提高元素查找效率。同时,NumPy数组的元素可以通过基于0的下标单独访问。NumPy数组还通过dtype和shape属性表示元素的类型和维度,其中维度的类型是元组,按照从高到低的顺序来排列每一维的大小。
NumPy的优点在于其提供了大量数值计算的函数,能够进行线性代数的相关操作,并且由于其底层用C编写,因此执行效率非常高。这使得NumPy在科学计算、数据分析、机器学习、深度学习以及人工智能等领域有着广泛的应用。
安装NumPy的方法有多种,包括使用pip、conda或者从源码进行安装。在命令行中输入pip install numpy即可从Python官方的包索引中下载和安装最新版的NumPy。如果需要安装特定版本的NumPy,可以在命令中指定版本号,例如pip install numpy==1.19.3将安装NumPy的1.19.3版本。
简单举例:
以下是一些NumPy的简单使用例子:
- 创建数组:
使用np.array()函数可以直接创建一个NumPy数组。
import numpy as np | |
# 创建一个一维数组 | |
arr1 = np.array([1, 2, 3, 4, 5]) | |
print(arr1) # 输出: [1 2 3 4 5] | |
# 创建一个二维数组 | |
arr2 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) | |
print(arr2) | |
# 输出: | |
# [[1 2 3] | |
# [4 5 6] | |
# [7 8 9]] |
2.基本数学运算:
NumPy支持对数组进行基本的数学运算,如加法、减法、乘法、除法等。
# 创建两个数组 | |
a = np.array([1, 2, 3]) | |
b = np.array([4, 5, 6]) | |
# 数组加法 | |
c = a + b | |
print(c) # 输出: [5 7 9] | |
# 数组乘法 | |
d = a * b | |
print(d) # 输出: [ 4 10 18] |
3.索引和切片:
可以使用索引和切片来访问和修改数组中的元素。
# 使用索引访问数组元素 | |
element = arr2[0, 1] # 访问第一行第二列的元素 | |
print(element) # 输出: 2 | |
# 使用切片访问数组的子集 | |
subset = arr2[:2, 1:] # 访问前两行,从第二列开始到最后的所有列 | |
print(subset) | |
# 输出: | |
# [[2 3] | |
# [5 6]] |
4.创建特殊数组:
NumPy提供了创建特殊类型数组的函数,如零数组、一数组、等差数组等。
# 创建零数组 | |
zeros_arr = np.zeros((3, 3)) | |
print(zeros_arr) | |
# 输出: | |
# [[0. 0. 0.] | |
# [0. 0. 0.] | |
# [0. 0. 0.]] | |
# 创建一数组 | |
ones_arr = np.ones((2, 2), dtype=np.int) | |
print(ones_arr) | |
# 输出: | |
# [[1 1] | |
# [1 1]] | |
# 创建等差数组 | |
linspace_arr = np.linspace(0, 10, 5) # 从0到10,生成5个数 | |
print(linspace_arr) # 输出: [ 0. 2.5 5. 7.5 10. ] |
NumPy作为Python中科学计算的基础包,功能丰富且强大,除了上述的基本功能外,还有许多其他高级功能。以下是一些NumPy的高级功能示例:
1.数组重塑:
NumPy提供了reshape方法,允许用户改变数组的形状而不改变其数据。例如,你可以将一个一维数组重塑为二维数组,或者将一个二维数组重塑为三维数组等。
import numpy as np | |
a = np.array([1, 2, 3, 4, 5, 6]) | |
b = a.reshape(2, 3) | |
print(b) | |
# 输出: | |
# [[1 2 3] | |
# [4 5 6]] |
2.数组合并:
使用np.concatenate函数,你可以沿着指定的轴将多个数组合并成一个数组。
a = np.array([1, 2, 3]) | |
b = np.array([4, 5, 6]) | |
c = np.concatenate((a, b)) | |
print(c) | |
# 输出: [1 2 3 4 5 6] |
3.布尔索引:
通过布尔索引,你可以基于条件选择数组中的元素。
arr = np.array([1, 2, 3, 4, 5]) | |
filtered_arr = arr[arr > 3] | |
print(filtered_arr) | |
# 输出: [4 5] |
4.花式索引:
花式索引允许你使用整数数组来索引数组中的元素。这可以用于选择非连续的元素或进行复杂的切片操作。
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) | |
selected_elements = arr[[0, 1, 2], [0, 1, 2]]#在NumPy中,使用两个整数数组进行索引时,第一个数组指定了行索引,第二个数组指定了列索引。这种方式被称为“花式索引”或“高级索引”。 | |
print(selected_elements) | |
# 输出: [1 5 9] 这里的 arr[[0, 1, 2], [0, 1, 2]] 实际上选择的是 (0, 0), (1, 1), 和 (2, 2) 这三个位置的元素,即对角线元素。 |
5.线性代数运算:
NumPy提供了许多线性代数函数,如矩阵乘法、矩阵转置、求解线性方程组、计算特征值和特征向量等。
A = np.array([[1, 2], [3, 4]]) | |
B = np.array([[5, 6], [7, 8]]) | |
C = np.dot(A, B) # 矩阵乘法 | |
print(C) | |
# 输出: | |
# [[19 22] | |
# [43 50]] |
6.随机数生成:
NumPy提供了多种随机数生成函数,可以用于生成均匀分布、正态分布等不同分布的随机数。
# 生成0到1之间的随机浮点数 | |
random_float = np.random.rand() | |
print(random_float) | |
# 生成形状为(3, 3)的随机数矩阵 也是01之间的数 | |
random_matrix = np.random.rand(3, 3) | |
print(random_matrix) |
如果随机数矩阵不在0到1之间,而是具有其他范围或分布,NumPy提供了多种函数来满足这些需求。以下是一些常用的方法:
- 指定范围:使用
np.random.uniform函数可以指定随机数的下限和上限。
import numpy as np | |
# 生成形状为(3, 3)的随机数矩阵,元素范围在a和b之间 | |
a, b = 5, 10 # 指定范围 | |
random_matrix = np.random.uniform(a, b, size=(3, 3)) | |
print("随机数矩阵:\n", random_matrix) |
2.整数随机数:使用np.random.randint函数可以生成指定范围内的整数随机数。
import numpy as np | |
# 生成形状为(3, 3)的整数随机矩阵,元素范围在low和high之间(包括low,不包括high) | |
low, high = 5, 10 # 指定范围 | |
random_matrix = np.random.randint(low, high, size=(3, 3)) | |
print("整数随机数矩阵:\n", random_matrix) |
3.正态分布:使用np.random.randn或np.random.normal函数可以生成符合正态分布的随机数。
import numpy as np | |
# 生成形状为(3, 3)的正态分布随机数矩阵,均值为mu,标准差为sigma | |
mu, sigma = 0, 1 # 均值和标准差 | |
random_matrix = np.random.normal(mu, sigma, size=(3, 3)) | |
print("正态分布随机数矩阵:\n", random_matrix) |
3.其他分布:NumPy还提供了其他分布,如指数分布(np.random.exponential)、泊松分布(np.random.poisson)等,您可以根据需要选择合适的函数。
请注意,上述函数中的size参数用于指定输出数组的形状。如果您想生成一个3x3的矩阵,就应该将size设置为(3, 3)。此外,还可以通过调整分布的参数(如均值、标准差、范围等)来控制随机数的特性。
这些只是NumPy功能的冰山一角。NumPy还提供了大量的数学函数、统计函数、线性代数函数等,可以方便地处理各种数值计算任务。无论是数据科学、机器学习还是科学计算,NumPy都是一个非常强大的工具。
总的来说,NumPy是一个强大且灵活的工具,对于需要进行数值计算和数据处理的任务来说,它是一个不可或缺的选择。
相关文章:

浅述python中NumPy包
NumPy(Numerical Python)是Python的一种开源的数值计算扩展,提供了多维数组对象ndarray,是一个快速、灵活的大数据容器,可以用来存储和处理大型矩阵,支持大量的维度数组与矩阵运算,并针对数组运…...

jvm的面试回答
1、jvm由本地方法栈、虚拟机栈、方法区、程序计数器、堆组成,其中堆和方法区是线程间共享的,程序计数器、虚拟机栈和本地方法栈是线程私有的。 2、虚拟机栈: 保存每个java方法的调用、保存局部变量表、等 栈可能出现内存溢出,如果…...

打不动的蓝桥杯
打不动的蓝桥杯 2024-4-13 今天的蓝桥杯打得很烂,8题写了4题,100分可能有20来分吧。我写了的题好像都很简单,没什么竞争力。又觉得我知道的东西不止这么点,没能发挥。 这次比赛,首先,有强烈的陌生感。pytho…...
)
学习笔记——C语言基本概念文件——(13)
1、文件操作 1.1、文件概念 文件:实现数据存储的载体 1.2、文件的分类 按照数据的组织形式分类: 1.字符文件/文本文件 2.二进制文件 按照用途分类: 1.系统文件 2.库文件--标准库文件/非标准库文件(第三方库) 3.用…...
【MySQL】事务篇
SueWakeup 个人主页:SueWakeup 系列专栏:学习技术栈 个性签名:保留赤子之心也许是种幸运吧 目录 本系列专栏 1. 什么是事务 2. 事务的特征 原子性(Atomicity) 一致性(Consistency) 隔离性&…...
tsconfig.json文件常用配置
最近在学ts,因为tsconfig的配置实在太多啦,所以写此文章用作记录,也作分享 作用? tsconfig.jsono是ts编译器的配置文件,ts编译器可以根据它的信息来对代码进行编译 初始化一个tsconfig文件 tsc -init配置参数解释 …...

【Linux】tcpdump P1 - 网络过滤选项
文章目录 选项 -D选项 -c X选项 -n选项 -s端口捕获 port选项 -w总结 tcpdump 实用程序用于捕获和分析网络流量。系统管理员可以使用它来查看实时流量或将输出保存到文件中稍后分析。本文将演示在日常使用 tcpdump时可能想要使用的几种常见选项。 选项 -D 使用-D 选项的 tcpdu…...
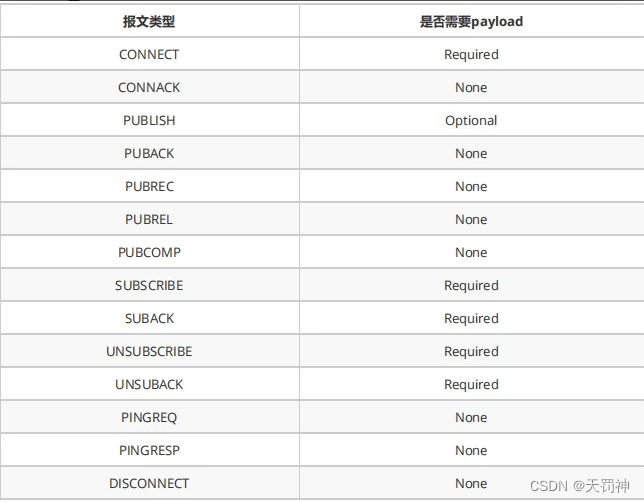
网络篇04 | 应用层 mqtt(物联网)
网络篇04 | 应用层 mqtt(物联网) 1. MQTT协议介绍1.1 MQTT简介1.2 MQTT协议设计规范1.3 MQTT协议主要特性 2 MQTT协议原理2.1 MQTT协议实现方式2.2 发布/订阅、主题、会话2.3 MQTT协议中的方法 3. MQTT协议数据包结构3.1 固定头(Fixed header…...

Transformer模型-decoder解码器,target mask目标掩码的简明介绍
今天介绍transformer模型的decoder解码器,target mask目标掩码 背景 解码器层是对前面文章中提到的子层的包装器。它接受位置嵌入的目标序列,并将它们通过带掩码的多头注意力机制传递。使用掩码是为了防止解码器查看序列中的下一个标记。它迫使模型仅使用…...

All in One:Prometheus 多实例数据统一管理最佳实践
作者:淡唯(啃唯)、阳其凯(逸陵) 引言 Prometheus 作为目前最主流的可观测开源项目之一,已经成为云原生监控的事实标准,被众多企业广泛应用。在使用 Prometheus 的时候,我们经常会遇…...
mysql报错-mysql服务启动停止后,某些服务在未由其他服务或程序使用时将自动停止和数据恢复
启动mysql服务时出现该错误: 本地计算机上的mysql服务启动停止后,某些服务在未由其他服务或程序使用时将自动停止。 我的mysql版本是8.0.18 系统:win10 如何安装mysql,可以看我这一篇文章:mysql的安装 ---必会 - bigbigbrid - 博客园 (cn…...

Java开发从入门到精通(二十):Java的面向对象编程OOP:File文件操作的增删改查
Java大数据开发和安全开发 (一)Java的文件操作1.1 Java的File和IO流概念1.2 File类的使用1.2.1 创建File类的对象1.2.2 常用方法1:判断文件类型、获取文件信息1.2.3 常用方法2:创建文件、删除文件1.2.4 常用方法3:遍历文件夹 1.3 java File的方法递归1.3…...
)
10.list的模拟实现(普通迭代器和const迭代器的类模板)
1. list的介绍及使用 1.1 list的介绍 list的文档介绍 list是可以在常数范围内在任意位置进行插入和删除的序列式容器,并且该容器可以前后双向迭代。 list的底层是双向链表结构,双向链表中每个元素存储在互不相关的独立节点中,在节点中通过…...
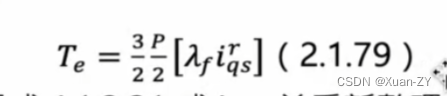
【电控笔记5】电流环速度环三环参数整定
旋转坐标系下的电压方程,由id和iq计算出ud和uq Lq:q轴电感 Ld:d轴电感 输入是电流,输出是电压? 内嵌式pmsm(ipmsm)模型建立: 其中: λf是转子磁场在定子绕组所产生的磁通链,为一常数,在psms中转子磁场非常稳定几乎不变。 ipmsm转矩方程式: 对永磁同步马达而言,使…...

AI克隆语音(基于GPT-SoVITS)
概述 使用GPT-SoVITS训练声音模型,实现文本转语音功能。可以模拟出语气,语速。如果数据质量足够高,可以达到非常相似的结果。相比于So-VITS-SVC需要的显卡配置更低,数据集更小(我的笔记本NVIDIA GeForce RTX 4050 Lap…...

小蚕爬树问题
小蚕爬树问题 问题描述: 编写一个函数 int day(int k,int m,int n),其功能是:返回小蚕需要多少天才能爬到树顶(树高 k 厘米,小蚕每天白天向上爬 m 厘米,每天晚上下滑 n 厘米,爬到树顶后不再下滑࿰…...
科研学习|科研软件——如何使用SmartPLS软件进行结构方程建模
SmartPLS是一种用于结构方程建模(SEM)的软件,它可以用于定量研究,尤其是在商业和社会科学领域中,如市场研究、管理研究、心理学研究等。 一、准备数据 在使用SmartPLS之前,您需要准备一个符合要求的数据集。…...
实用工具系列-ADB使用方式
作者持续关注 WPS二次开发专题系列,持续为大家带来更多有价值的WPS开发技术细节,如果能够帮助到您,请帮忙来个一键三连,更多问题请联系我(WPS二次开发QQ群:250325397),摸鱼吹牛嗨起来࿰…...

计算机网络书籍--《网络是怎样连接的》阅读笔记
第一章 浏览器生成信息 1.1 生成HTTP请求信息 1.1.1 URL Uniform Resource Locator, 统一资源定位符。就是网址。 不同的URL能够用来判断使用哪种功能来访问相应的数据,比如访问Web服务器就要用”http:”,而访问FTP服务器用”ftp:”。 FTPÿ…...

antd+vue——datepicker日期控件——禁用日期功能
需求:今天之前的日期禁用 <a-date-pickerv-model.trim"formNE.deliveryTime":disabled-date"disabledDate"valueFormat"YYYY-MM-DD"allowClearstyle"width: 100%" />禁用日期的范围: //时间范围 disab…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
