当前位置： 首页 > news >正文

Docker安装Kong网关

news 2026/2/7 18:49:55

文章目录

  • 一、kong是什么？
  • 二、搭建步骤
    • 1.搭建PostgreSQL
    • 2.搭建Kong网关
      • 2.1、制作镜像
      • 2.2、数据库初始化
      • 2.3、启动Kong网关

一、kong是什么？

Github地址：https://github.com/Kong/kong

Kong是一个可扩展、开源的云原生API网关，可以在分布式环境中管理、监控和安全地发布API。它基于nginx，但比nginx更加强大和灵活。Kong的主要作用是为API提供保护、安全性、可伸缩性和可控性，实现动态配置，并基于插件化实现更多功能，如身份认证、请求限流、黑白名单配置等。

Kong网关可以处理流量路由、请求的验证和授权、负载均衡、缓存、日志记录和监控等任务。它可以根据配置规则路由传入的请求，将请求发送到不同的后端服务上。基于URL、HTTP方法、请求头和查询参数等进行请求路由。此外，Kong网关还可以处理用户验

相关文章：

Docker安装Kong网关

文章目录 一、kong是什么？二、搭建步骤1.搭建PostgreSQL2.搭建Kong网关2.1、制作镜像2.2、数据库初始化2.3、启动Kong网关一、kong是什么？ Github地址：https://github.com/Kong/kong Kong是一个可扩展、开源的云原生API网关，可以在分布式环境中管理、监控和安全地发布API…...

编程日记 2024/4/17 2:58:02

spispispi

SPI C.. & C.. logic是SPI的控制逻辑，芯片内部进行地址锁存、数据读写等操作，都是由控制逻辑自动完成。控制逻辑的左边是SPI的通信引脚，这些引脚和主控芯片相连，主控芯片通过SPI协议，把指令和数据发送给控制逻辑&a…...

编程日记 2024/4/17 2:55:58

MySQL——创建和插入

一、插入数据 INSERT 使用建议; 在任何情况下建议列出列名，在 VALUES 中插入值时，注意值和列的意义对应关系 values 指定的值顺序非常重要，决定了值是否被保存到正确的列中 在指定了列名的情况下，你可以仅对需要插入的列给到…...

编程日记 2024/4/17 2:50:50

【BUG】element-ui表格中使用video标签，数据翻页，video中的视频仍然显示第一页的视频，没有重新加载

BUG描述 遇到一个问题&#xff0c;使用element-ui构建的管理端后台&#xff0c;表格里面每一行都有一个video标签&#xff0c;里面有视频&#xff0c;当我翻页了以后&#xff0c;视频不会重新加载&#xff0c;仍然显示的是第一页的视频&#xff0c;代码如下&#xff1a; <e…...

编程日记 2024/4/17 2:49:49

【JavaSE】你真的了解内部类吗？

前言 本篇会详细讲解内部类的四种形式&#xff0c;让你掌握内部类~ 欢迎关注个人主页&#xff1a;逸狼 创造不易&#xff0c;可以点点赞吗~ 如有错误&#xff0c;欢迎指出~ 目录 前言 内部类介绍 实例内部类 定义 调用 静态内部类 定义 调用 匿名内部类 定义和调用1 调用方法2 …...

编程日记 2024/4/17 2:48:48

Vue3（二）：报错调试，vue3响应式原理、computed和watch,ref,props,接口

一、准备工作调试 跟着张天禹老师看前几集的时候可能会遇到如下问题&#xff1a; 1.下载插件&#xff1a;Vue Language Features (Volar)或者直接下载vue-offical 2.npm run serve时运行时出现错误&#xff1a;Error: vitejs/plugin-vue requires vue (&#xff1e;3.2.13) …...

编程日记 2024/4/17 2:45:45

前端console用法分享

console对于前端人员来讲肯定都不陌生&#xff0c;相信大部分开发者都会使用console来进行调试&#xff0c;但它能做的绝不仅限于调试。 最常见的控制台方法 作为开发者&#xff0c;最常用的 console 方法如下&#xff1a; 控制台打印结果&#xff1a; 今天我分享的是一些 co…...

编程日记 2024/4/17 2:39:37

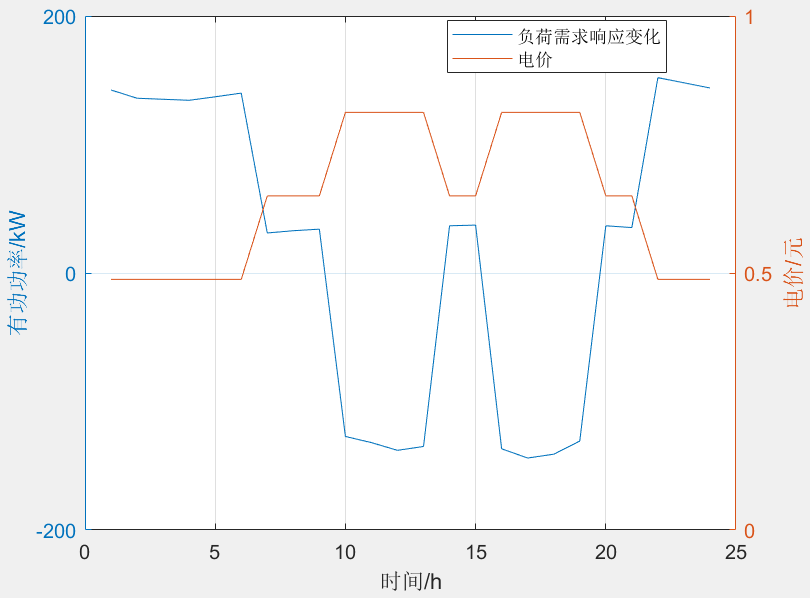
Matlab|电价型负荷需求响应（考虑电价变化）

程序复现来源于《计及需求响应消纳风电的电-热综合能源系统经济调度 》第四章内容。 一、原理 需求响应的基本原理是需求侧根据电力市场价格和电网要求改变其负荷需求以 获取一定的利益回报。其中 PDR 可通过直观的电价变化信号引导用户调节用电方式&#xff0c; 从而达到优…...

编程日记 2024/4/17 2:37:35

PySide QWebChannel实现Python与JS双向通信的前后端分离桌面应用

文章目录 一、前言二、实现方法1.前端部分2.后端部分3.依赖文件三、运行结果一、前言 以往开发桌面应用通常都是页面接口一起写，这样开发周期比较长，且页面样式不灵活，如果能把页面交给前端写的话，就可前后端并行开发桌面应用了，并且css语言灵活好用样式丰富。下面介绍一…...

编程日记 2024/4/17 2:36:33

清明三天，用Python赚了4万？

每年4月&#xff0c;是Python圈子里接私活的旺季&#xff0c;特别是在节假日这种数据暴增的时间段&#xff0c;爬虫采集、逆向破解类的私活订单会集中爆发&#xff0c;量大价高。几乎所有的圈内人都在趁着旺季接私活。 正好&#xff0c;我昨天就做了一单爬虫逆向私活&#xff…...

编程日记 2024/4/17 2:35:32

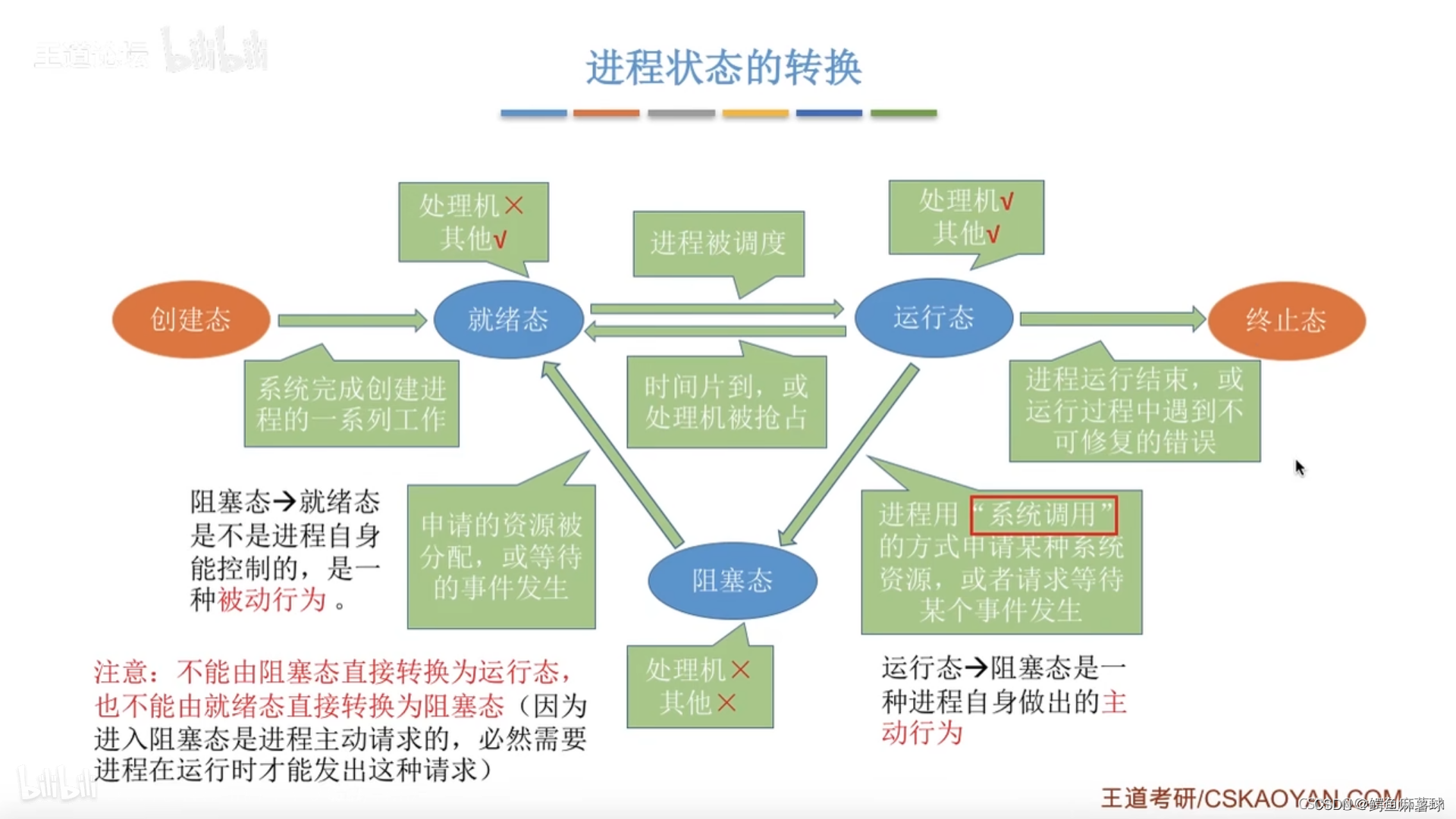
【C/C++笔试练习】read函数、虚拟存储、用户态、线程特点、缺页处理、调度算法、进程优先级、锁的使用、创建进程、不用加减乘除做加法、三角形

文章目录 C/C笔试练习选择部分&#xff08;1&#xff09;read函数&#xff08;2&#xff09;虚拟存储&#xff08;3&#xff09;用户态&#xff08;4&#xff09;线程特点&#xff08;5&#xff09;缺页处理&#xff08;6&#xff09;调度算法&#xff08;7&#xff09;进程优先…...

编程日记 2024/4/17 2:31:25

设计模式(021)行为型之访问者模式

访问者模式是一种行为型设计模式&#xff0c;它可以在不修改现有代码结构的情况下&#xff0c;为复杂的对象结构添加新的操作。该模式将数据结构和数据操作进行分离&#xff0c;使得数据结构可以独立于操作进行变化&#xff0c;同时也可以在不改变操作的前提下增加新的操作。 在…...

编程日记 2024/4/17 2:30:24

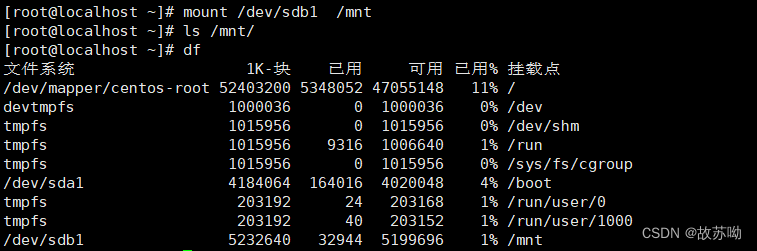
Linux中磁盘的分区，格式化，挂载和文件系统的修复

一.分区工具 1.分区工具介绍 fdisk 2t及以下分区 推荐 (分完区不保存不生效&#xff0c;有反悔的可能) gdisk 全支持 推荐 parted 全支持 不推荐 ( 即时生效&#xff0c;分完立即生效) 2.fdisk 分区,查看磁盘 格式:fdisk -l [磁盘设备] fdisk -l 查看…...

编程日记 2024/4/17 2:28:22

Android retrofit

目录 一.简介 二.基本使用 三.注解 四.转换器 五.适配器 六.文件上传与下载 一.简介 A type-safe HTTP client for Android and Java。封装了OkHttp&#xff0c;也是由Square公司贡献的一个处理网络请求的开源项目。 square/retrofit: A type-safe HTTP client for Andr…...

编程日记 2024/4/17 2:26:21

【C++风云录】五款 C++ 库的探索与应用：物联网、嵌入式与数据处理

提升你的C技能&#xff1a;五个关键库的使用与指南 前言 在今天的数字化世界里&#xff0c;C 作为一种强大且快速的编程语言&#xff0c;在各类复杂系统和应用的开发中扮演着重要角色。然而&#xff0c;单凭语言本身的能力&#xff0c;我们往往无法实现所有的功能需求&#x…...

编程日记 2024/4/17 2:25:20

Qt_30道常见面试题及答案

1. 简述 Qt 是什么&#xff1f; 答&#xff1a;Qt 是一个跨平台的应用程序开发框架&#xff0c;它提供了一系列的工具和库&#xff0c;用于开发图形用户界面&#xff08;GUI&#xff09;应用程序。 2. Qt 有哪些主要模块&#xff1f; 答&#xff1a;Qt 的主要模块包括 Qt Co…...

编程日记 2024/4/17 2:24:18

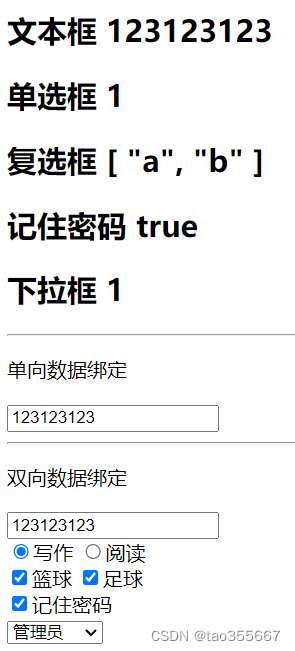
【vue】v-model 双向数据绑定

:value&#xff1a;单向数据绑定v-model&#xff1a;双向数据绑定 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0">…...

编程日记 2024/4/17 2:23:16

C#创建磁性窗体的方法：创建特殊窗体

目录 一、磁性窗体 二、磁性窗体的实现方法 (1)无标题窗体的移动 (2)Left属性 (3)Top属性 二、设计一个磁性窗体的实例 &#xff08;1&#xff09;资源管理器Resources.Designer.cs设计 &#xff08;2&#xff09;公共类Frm_Play.cs &#xff08;3&#xff09;主窗体 …...

编程日记 2024/4/17 2:21:14

Gateway 基本配置指南：构建高效的网络接入网关

简介&#xff1a; Gateway 是一个常用的网络接入网关&#xff0c;它可以帮助组织实现安全、可靠和高性能的网络连接。本文将介绍 Gateway 的基本配置&#xff0c;帮助读者了解如何正确配置和部署一个高效的 Gateway 网关。 1.网络拓扑规划&#xff1a; 在配置 Gateway 前&#…...

编程日记 2024/4/17 2:16:08

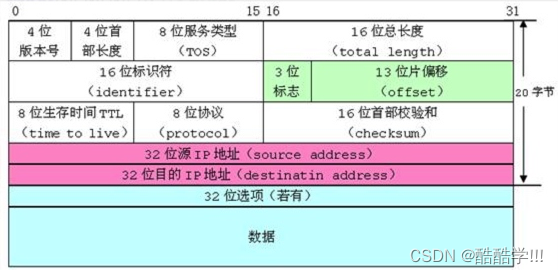
自定义类型: 结构体 (详解)

本文索引 一. 结构体类型的声明1. 结构体的声明和初始化2. 结构体的特殊声明3. 结构体的自引用 二. 结构体内存对齐1. 对齐规则2. 为啥存在对齐?3. 修改默认对齐值 三. 结构体传参四. 结构体实现位段1. 什么是位段?2. 位段的内存分配3. 位段的应用4. 位段的注意事项 ​ 前言:…...

编程日记 2024/4/17 2:14:06

ESP32读取DHT11温湿度数据

芯片&#xff1a;ESP32 环境&#xff1a;Arduino 一、安装DHT11传感器库 红框的库&#xff0c;别安装错了 二、代码 注意&#xff0c;DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

编程新知 2026/1/30 8:46:45

CocosCreator 之 JavaScript/TypeScript和Java的相互交互

引擎版本&#xff1a; 3.8.1 语言&#xff1a; JavaScript/TypeScript、C、Java 环境&#xff1a;Window 参考&#xff1a;Java原生反射机制 您好&#xff0c;我是鹤九日&#xff01; 回顾 在上篇文章中&#xff1a;CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

编程新知 2026/1/30 12:10:19

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战

“&#x1f916;手搓TuyaAI语音指令 &#x1f60d;秒变表情包大师&#xff0c;让萌系Otto机器人&#x1f525;玩出智能新花样&#xff01;开整&#xff01;” &#x1f916; Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制&#xff08;TuyaAI…...

编程新知 2026/1/30 16:09:53

Element Plus 表单(el-form)中关于正整数输入的校验规则

目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入&#xff08;联动&#xff09;2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

编程新知 2025/11/10 19:08:45

稳定币的深度剖析与展望

一、引言 在当今数字化浪潮席卷全球的时代&#xff0c;加密货币作为一种新兴的金融现象&#xff0c;正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而&#xff0c;加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下&#xff0c;稳定…...

编程新知 2025/10/24 12:31:26

【生成模型】视频生成论文调研

工作清单 上游应用方向&#xff1a;控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

编程新知 2025/9/9 8:40:47

安宝特案例丨Vuzix AR智能眼镜集成专业软件，助力卢森堡医院药房转型，赢得辉瑞创新奖

在Vuzix M400 AR智能眼镜的助力下&#xff0c;卢森堡罗伯特舒曼医院&#xff08;the Robert Schuman Hospitals, HRS&#xff09;凭借在无菌制剂生产流程中引入增强现实技术&#xff08;AR&#xff09;创新项目&#xff0c;荣获了2024年6月7日由卢森堡医院药剂师协会&#xff0…...

编程新知 2026/1/24 13:01:05

深度学习水论文：mamba＋图像增强

&#x1f9c0;当前视觉领域对高效长序列建模需求激增&#xff0c;对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模&#xff0c;以及动态计算优势&#xff0c;在图像质量提升和细节恢复方面有难以替代的作用。 &#x1f9c0;因此短时间内&#xff0c;就有不…...

编程新知 2026/1/26 4:52:47

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程（6.3）

目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 ​编辑​编辑 UDP的特征 socke函数 bind函数 recvfrom函数&#xff08;接收函数&#xff09; sendto函数&#xff08;发送函数&#xff09; 五、网络编程之 UDP 用…...

编程新知 2026/2/6 5:57:59

机器学习的数学基础：线性模型

线性模型 线性模型的基本形式为&#xff1a; f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法&#xff0c;得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

编程新知 2025/10/2 9:07:50