概率论 科普
符号优先级
概率公式中一共有三种符号:分号 ; 、逗号 , 、竖线 | 。
; 分号代表前后是两类东西,以概率P(x;θ)为例,分号前面是x样本,分号后边是模型参数。分号前的 表示的是这个式子用来预测分布的随机变量x,分号后的 表示所需的相关参数θ。
, 逗号代表两个事件同时发生的概率,逗号连接两个事件,有时可以省略,如联合概率P(AB),等价于P(A,B)
| 竖线代表 if,以条件概率P(A|B)为例,A,B是随机试验E的两个随机试验,P(A|B)就是如果B事件发生的条件下,发生A事件的概率,结合图进行理解:
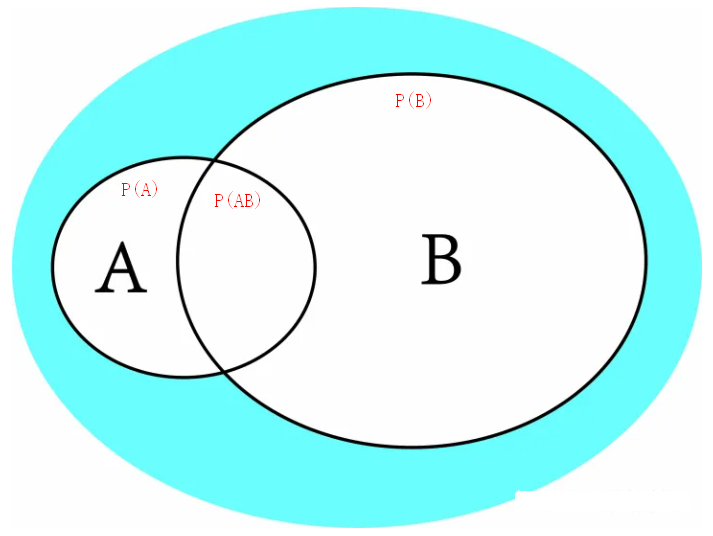
优先级: , > | > ;
例子1: P(A|B,C)表示在B,C的条件下,发生A的概率。
例子2:P(y∣x ; α,ω)表示:x发生条件下y的条件概率,该条件概率模型用参数α,ω建模(或者说用参数a,ω表示)。
注意:
p ( x ∣ θ ) p(x | \theta) p(x∣θ)不总是代表条件概率,也就是说 p ( x ∣ θ ) p(x | \theta) p(x∣θ) 不代表条件概率时与 p ( x ; θ ) p(x ; \theta) p(x;θ) 等价。而一般地,写竖杠表示条件概率,是随机变量。
p ( x ; θ ) p(x ; \theta) p(x;θ) 中,分号后的 表示待估参数(是固定的,只是当前未知),应该可以直接认为是 p ( x ) p(x) p(x),加了,是为了强调说明这里有个 θ \theta θ 的参数, p ( x ; θ ) p(x ; \theta) p(x;θ) 意思是随机变量 X = x X=x X=x 的概率。在 贝叶斯理论下又叫 X = x X=x X=x 的先验概率。
和 扩散模型推导公式的联系
根据以上讨论的这些,现在讨论一个比较复杂的情况。比如, N ( x ; 0 , I ) \mathcal{N}(x;0,I) N(x;0,I)的意思是什么?
我们知道, N ( 0 , I ) \mathcal{N}(0,I) N(0,I)表示标准高斯分布,均值为0,方差为1,其本质上也是一个概率密度函数 f ( x ) = 1 σ 2 π e − 1 2 ( x − μ σ ) 2 f(x) = \frac{1}{{\sigma \sqrt{2\pi}}} e^{ -\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} f(x)=σ2π1e−21(σx−μ)2(标准高斯分布情况下为 f ( x ) = 1 2 π e − x 2 2 f(x) = \frac{1}{{\sqrt{2\pi}}} e^{ -\frac{x^2}{2}} f(x)=2π1e−2x2 )。从这里可以发现,一般的函数我们都是强调自变量本身(比如 x x x),而在概率论里面有时候强调的是函数参数本身(比如高斯分布的均值和方差),而淡化了输入变量 x x x。因此 N ( x ; 0 , I ) \mathcal{N}(x;0,I) N(x;0,I)相比与 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)的区别就在于显式强调了函数的输入为 x x x。
这下,就好理解扩散模型中的噪声公式了:

那么, q ( x t ∣ x t − 1 ) = N ( x t ; 1 − β t x t − 1 , β t I ) q(x_t | x_{t-1})=\mathcal{N}(x_t; \sqrt{1-\beta_t }x_{t-1}, \beta_t I) q(xt∣xt−1)=N(xt;1−βtxt−1,βtI),这个公式何意义?
这个东西分多步看。首先,函数本身是个条件概率分布, q ( x t ∣ x t − 1 ) q(x_t | x_{t-1}) q(xt∣xt−1) 表示 x t − 1 x_{t-1} xt−1 已知的情况下, x t x_t xt 的分布 ( x t x_t xt取各种值的概率)。而后面的这个高斯分布则强调了其输入自变量为 x t x_t xt(因为是 x t x_t xt的概率密度函数,所以自变量当然是 x t x_t xt),而高斯分布的均值和方差则分别为
1 − β t x t − 1 和 β t I \sqrt{1-\beta_t }x_{t-1} 和 \beta_t I 1−βtxt−1和βtI,与条件分布的条件 x t − 1 x_{t-1} xt−1 有关。
全概率(概率函数连乘)

图示可表示为:
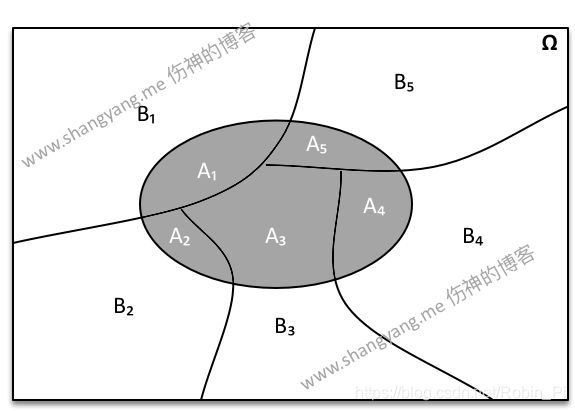
参考:
https://blog.csdn.net/shyjhyp11/article/details/133969095
相关文章:

概率论 科普
符号优先级 概率公式中一共有三种符号:分号 ; 、逗号 , 、竖线 | 。 ; 分号代表前后是两类东西,以概率P(x;θ)为例,分号前面是x样本,分号后边是模型参数。分号前的 表示的是这个式子用来预测分布的随机变量x,分号后的…...
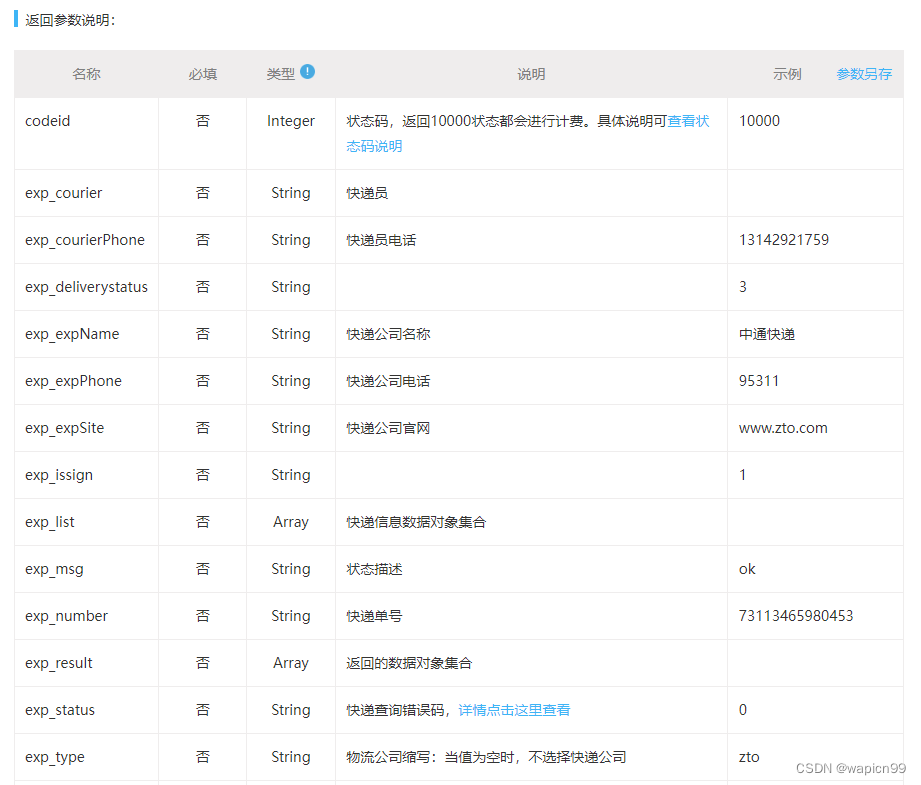
全面解读快递查询API接口,帮你轻松查询快递物流信息
随着电子商务的快速发展,快递业务正变得越来越重要。无论是买家还是卖家,都希望能够及时了解自己的快递物流信息,以便更好地掌控商品的运输过程。而现在,通过快递查询API接口,我们可以实现快速、准确地查询几百家国内快…...

【图书推荐】《JSP+Servlet+Tomcat应用开发从零开始学(第3版)》
本书目的 系统讲解JSPServletTomcat开发技术,帮助读者用最短的时间掌握Java Web应用开发技能。 内容简介 本书全面系统地介绍JSPServletTomcat开发中涉及的相关技术要点和实战技巧。本书内容讲解循序渐进,结合丰富的示例使零基础的读者能够熟练掌握JSP…...

C++容器——set
set容器 是一个关联容器,按一定的顺序存储一组唯一的元素。 set容器中的元素会根据元素的值自动进行排序,并且不允许包含重复的元素,基于二叉树实现的。 特点: 唯一性: set容器中的元素是唯一的,即容器中…...

.NET WebService \ WCF \ WebAPI 部署总结 以及 window 服务 调试
一、webservice 部署只能部署IIS上, 比较简单,就不做说明了 二、 WCF 部署 1 部署到IIS 跟部署 webservice 部署方法一样的 wcf 部署2 部署到控制台 要以管理员运行vs,或者 管理员运行 控制台的exe 在控制器项目中 创建IUserInfoService 接口…...
)
Centos系统实用运维命令记录(持续更新)
本文记录Centos服务器常用的运维命令,备忘 查询当前内存占用最高(前10)的进程列表和占用比例,进程ID ps -eo pid,comm,%mem,cmd --sort-%mem | head -n 11注: 内存警报时定位问题时非常有用 查询占用某个端口号的进程id lsof -i :9000注: 后面的9000…...

大势模方在修模过程中,如何导入su单体模型?
答:在单体化界面右键即可显示导入入口,若仍不可行,需要换最新版dv 模方是一款针对实景三维模型的冗余碎片、水面残缺、道路不平、标牌破损、纹理拉伸模糊等共性问题研发的实景三维模型修复编辑软件。模方4.1新增自动单体化建模功能ÿ…...

uniapp百度地图聚合
// loadBMap.js ak 百度key export default function loadBMap(ak) {return new Promise((resolve, reject) > {//聚合API依赖基础库,因此先加载基础库再加载聚合APIasyncLoadBaiduJs(ak).then(() > {// 调用加载第三方组件js公共方法加载其他资源库// 加载聚合API// Ma…...
nginx的应用部署nginx
这里写目录标题 nginxnginx的优点什么是集群常见的集群什么是正向代理、反向代理、透明代理常见的代理技术正向代理反向代理透明代理 nginx部署 nginx nginx(发音同enginex)是一款轻量级的Web服务器/反向代理服务器及电子邮件(IMAP/POP3&…...
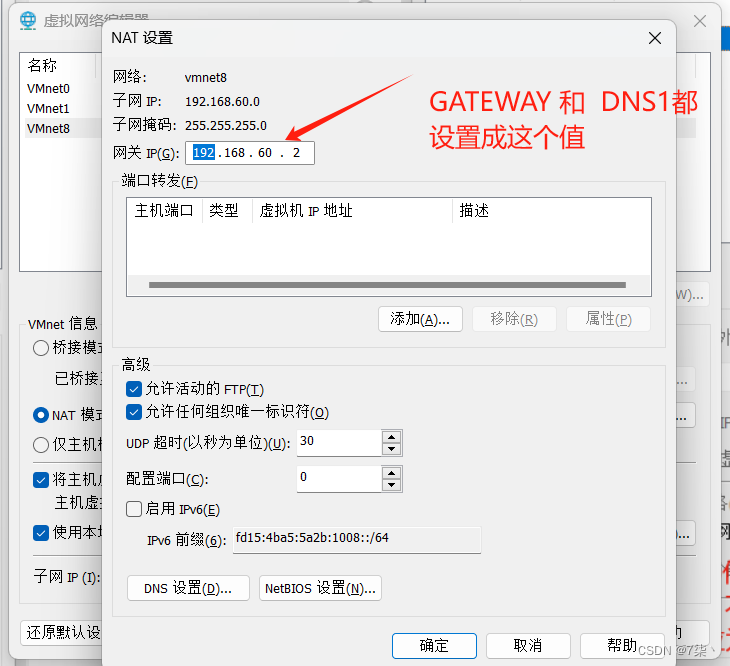
Centos固定静态ip地址
这里我用的是Vmware虚拟机搭建的三台机器 进入 cd /etc/sysconfig/network-scripts然后使用 ip addr命令,查看自己虚拟机的以太网地址。 我这里是ens33 上面的第一个选项是本地环回地址,不用管它 然后查看刚刚进入的network-scripts目录下的文件 找到…...

豆芽机置入语音芯片WTN6040-8S:开启智能生活新篇章,让豆芽制作更便捷有趣
豆芽机的开发背景: 豆芽作为一种营养丰富、味道鲜美的食品,深受广大消费者的喜爱。然而,传统的豆芽生产过程繁琐,需要耗费大量的时间和人力,且存在生产效率低、质量不稳定等问题。随着人们生活节奏的加快和对健康饮食的…...
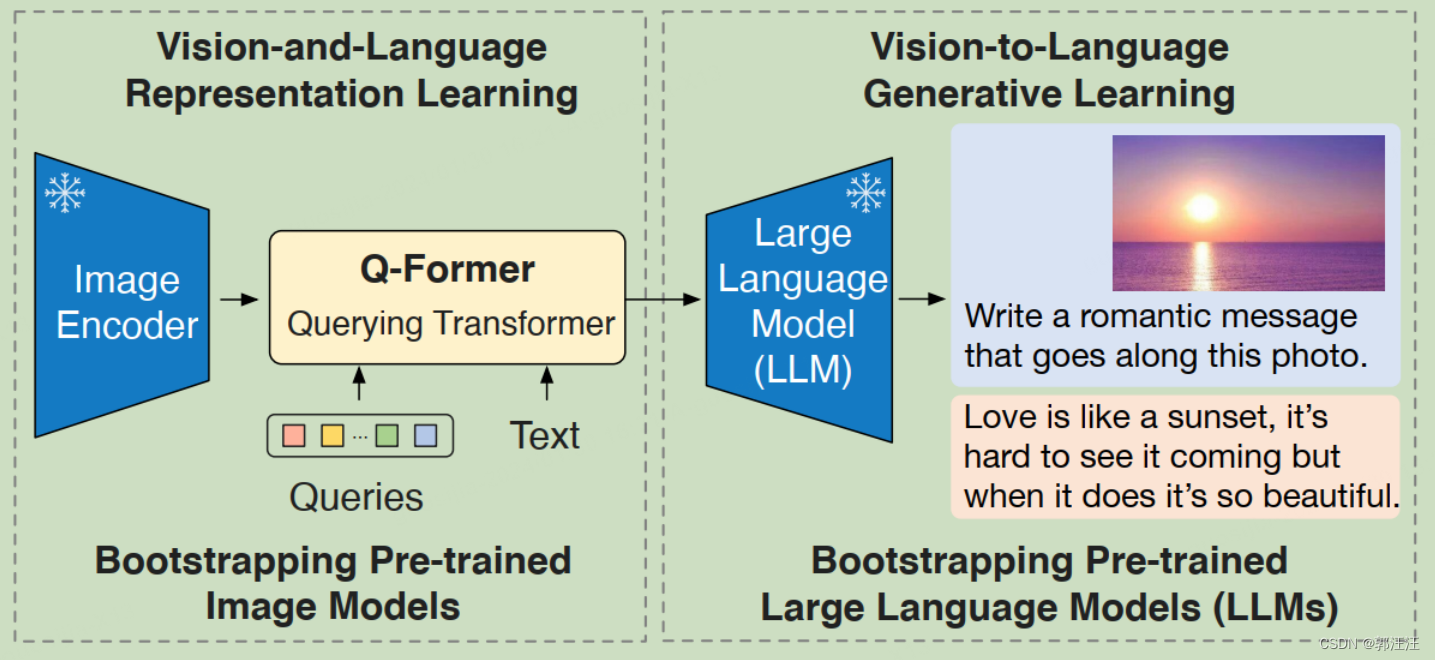
BLIP2预研笔记
0. 前言 文章是公司内部分享学习写的预研报告,里面有小部分文段是直接从网上借鉴的,侵删 1. 任务和方法历史进化: 在大模型等类似的预训练模型的方式(以包含“预训练阶段”等n阶段训练方式为特色)为主流之前…...

安卓开发问题:安卓Ble出现动态鉴权失败以及扫描设备一直进入不了的问题
问题1描述 1、安卓12需要动态鉴权 // 鉴权函数 requestPermissions(permissionsList.toArray(strings), MyConstants.REQUEST_CODE_PERMISSIONS);但是在鉴权回调函数中如Manifest.permission.BLUETOOTH_SCAN、Manifest.permission.BLUETOOTH_CONNECT一直显示失败&…...
DSP ARM FPGA 实验箱_音频处理_滤波操作教程:3-9 音频信号的滤波实验
一、实验目的 掌握Matlab辅助设计滤波器系数的方法,并实现音频混噪及IIR滤波器滤除,并在LCD上显示音频信号的FFT计算结果。 二、实验原理 音频接口采用的是24.576MHz(读兆赫兹)晶振,实验板上共有3个音频端口&#x…...

Rust多线程交叉打印+Send Sync特征讲解
导航 Rust多线程交叉打印Send Sync特征讲解 一、Rust多线程交叉打印二、Send Sync 特征讲解 Rust多线程交叉打印Send Sync特征讲解 一、Rust多线程交叉打印 先说背景有两个线程,分别为0号线程和1号线线程两个线程交叉打印共享值,并将共享值1当标志为fa…...

C#爬虫爬取某东商品信息
🏆作者:科技、互联网行业优质创作者 🏆专注领域:.Net技术、软件架构、人工智能、数字化转型、DeveloperSharp、微服务、工业互联网、智能制造 🏆欢迎关注我(Net数字智慧化基地),里面…...
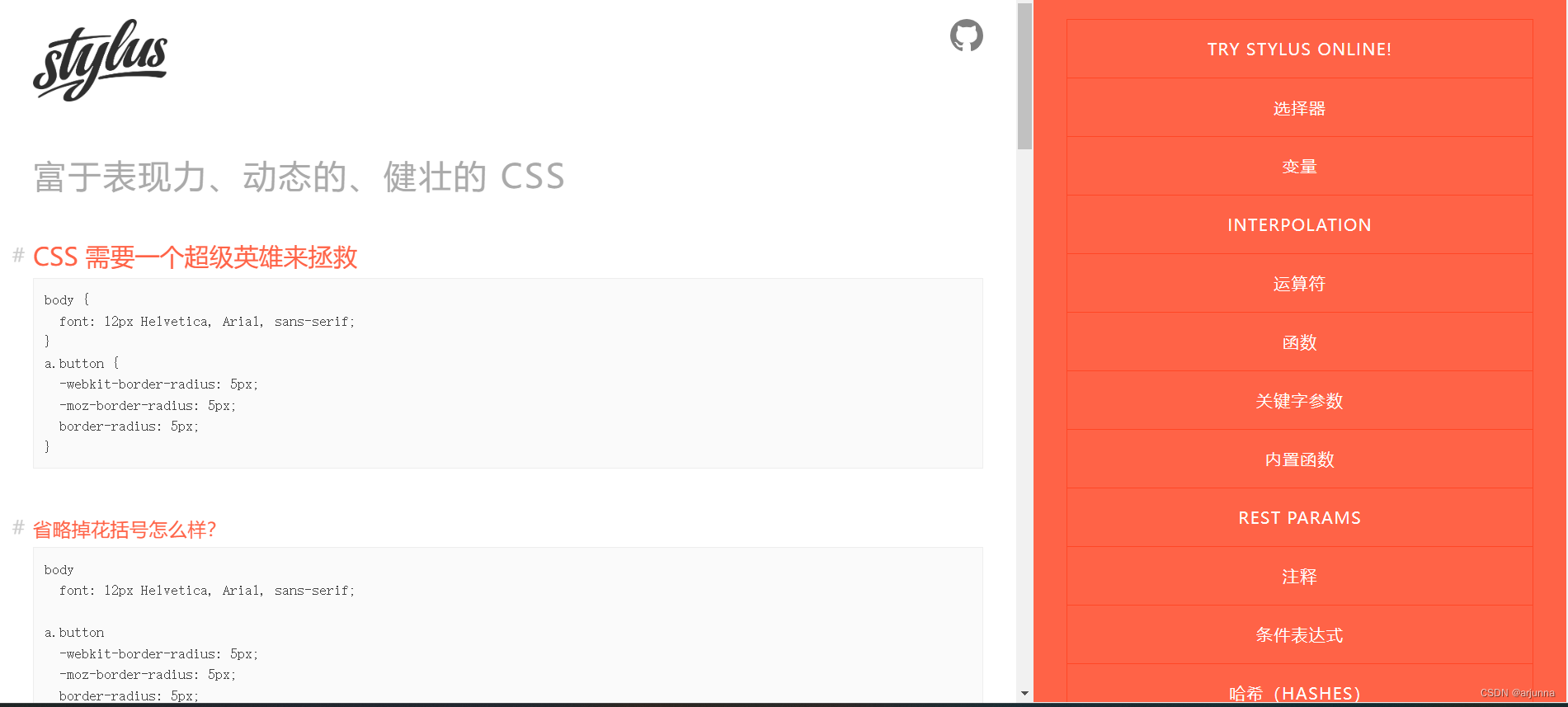
【Stylus详解与引入】
文章目录 Stylus详解与引入一、Stylus简介二、Stylus的特性1. 变量2. 嵌套规则3. 混合(Mixins)4. 函数5. 条件语句和循环 三、Stylus的引入与配置1. 安装Stylus和stylus-loader2. 配置Webpack3. 在Vue项目中使用Stylus4. 编译Stylus代码四、Stylus的性能…...
)
001 登录(md5加密)
文章目录 pom.xmlLoginController.javaUserMapper.javaUser.javaUserServiceImpl.javaUserService.javaMD5Util.javaMD5UtilTest.javaValidatorUtil.javaLoginVo.javaRespBean.javaRespBeanEnum.javaSeckillApplication.javaUserMapper.xmllogin.htmlapplication.yamlsql 传统方…...
Linux学习笔记5---WSL2编译裸机程序并烧录至SD卡
在用WLS进行开发的时候发现在mnt/底下竟然识别不了U盘!!也识别不了SD卡!!那程序不就不能烧录到SD卡上了???那还开发个锤子。 在网上查找了一些相关资料,发现可以通过Win32DiskImager…...
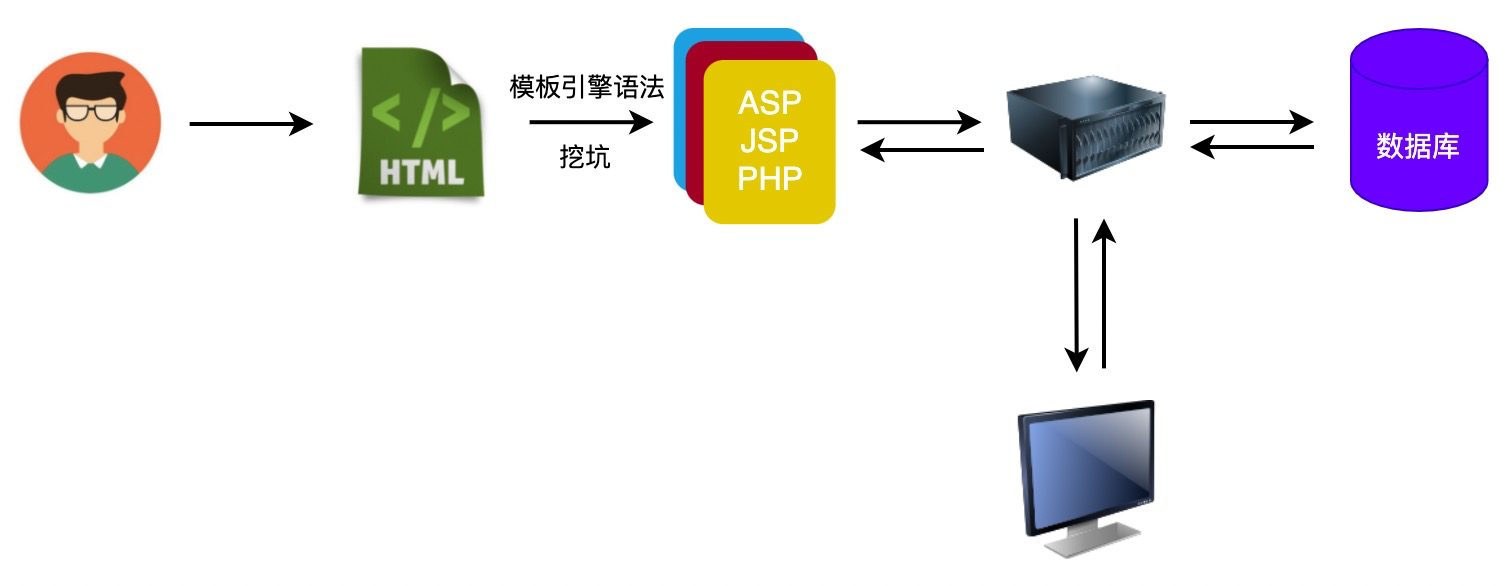
React 第二十九章 React 和 Vue 描述页面的区别
面试题:React 和 Vue 是如何描述 UI 界面的?有一些什么样的区别? 标准且浅显的回答: React 中使用的是 JSX,Vue 中使用的是模板来描述界面 前端领域经过长期的发展,目前有两种主流的描述 UI 的方案…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
