快速了解原码、反码、补码和位运算
我们知道计算机使用的是二进制,我们⽤⼀个字节,也就是8个bit 来表示⼆进制数。
原码
| 十进制 | 原码 |
| 2 | 0000 0010 |
| -2 | 1000 0010 |
原码其实是最容易理解的,只不过需要利⽤⼆进制中的第⼀位来表示符号位,0表示正数,1表示负数,所 以可以看到,⼀个数字⽤⼆进制原码表示的话,取值范围是 -111 1111 ~ +111 1111 ,换成⼗进制就 是 -127 ~ 127 。
反码
对于计算机来说最好只有加法,这样计算机会更加简单⾼效,我们知道在数学中 5-3=2 ,其实可以转换成 5+(-3)=2 ,这就表示减法可以⽤加法表示,⽽乘法是加法的累积,除法是减法的累积,所以在计算机中只要有加法就够了。 ⼀个数字⽤原码表示是容易理解的,但是需要单独的⼀个bit来表示符号位。并且在进⾏加法时,计算机需要先识别某个⼆进制原码是正数还是负数,识别出来之后再进⾏相应的运算。这样效率不⾼,能不能让计 算机在进⾏运算时不⽤去管符号位,也就是说让符号位也参与运算,这就要⽤到反码。
| 十进制 | 原码 | 反码 |
| 2 | 0000 0010 | 0000 0010 |
| -2 | 1000 0010 | 1111 1101 |
我们可以看到,对于正数,反码等于原码,对于负数就是符号位保持不变,其余各位对原码取反。那么我们来看⼀下,⽤反码直接运算会是什么情况,我们以 5-3 举例。
5 - 3 = 5+(-3)
| 十进制 | 原码 | 反码 |
| 5 | 0000 0101 | 0000 0101 |
| -3 | 1000 0011 | 1111 1100 |
5-3
= 5+(-3)
= 0000 0101(反码) + 1111 1100(反码)
= 0000 0001(反码)
= 0000 0001(原码)
= 1计算结果为1,为什么差了1?我们来看⼀个特殊的运算:1-1
1-1
= 1+(-1)
= 0000 0001(反码) + 1111 1110(反码)
= 1111 1111(反码)
= 1000 0000(原码)
= -0
0+0 运算如下:
0+0
= 0000 0000(反码) + 0000 0000(反码)
= 0000 0000(反码)
= 0000 0000(原码)
= 0从以上的运算中,我们可以看到1000 0000表示-0,0000 0000表示0,虽然-0和0是⼀样的,但是在⽤原码和反码表示时 是不同的,我们可以理解为在⽤⼀个字节表示数字取值范围时,这些数字中多了⼀个-0,所以导致我们在 ⽤反码直接运算时符号位可以直接参加运算,但是结果会不对。
补码
为了解决上面的问题,我们可以采用补码:
| 十进制 | 原码 | 反码 | 补码 |
| 2 | 0000 0010 | 0000 0010 | 0000 0010 |
| -2 | 1000 0010 | 1111 1101 | 1111 1110 |
也就是说:正数的补码和原码、反码⼀样,负数的补码就是反码+1。
| 十进制 | 原码 | 反码 | 补码 |
| 5 | 0000 0101 | 0000 0101 | 0000 0101 |
| -3 | 1000 0011 | 1111 1100 | 1111 1101 |
采用补码后,我们在来看5-3的执行过程:
5-3
= 5+(-3)
= 0000 0101(补码) + 1111 1101(补码)
= 0000 0010(补码)
= 0000 0010(原码)
= 25-3=2,结果真确。再来看一个特殊的:1-1
1-1
= 1+(-1)
= 0000 0001(补码) + 1111 1111(补码)
= 0000 0000(补码)
= 0000 0000(原码)
= 0继续:0+0
0+0
= 0000 0000(补码) + 0000 0000(补码)
= 0000 0000(补码)
= 0000 0000(原码)
= 0所以,我们可以看到补码解决了反码的问题。 所以对于数字,我们可以使⽤补码的形式来进⾏⼆进制表示。
位移运算
java中的位移运算有:
< 左移
> 右移
>>> ⽆符号右移
正数位移运算
System.out.println(2 << 1); // 4
System.out.println(2 >> 1); // 1
System.out.println(2 >>> 1); // 1
System.out.println(-2 << 1); // -4
System.out.println(-2 >> 1); // -1
System.out.println(-2 >>> 1); // 2147483647乍⼀眼看到上⾯Demo的打印结果,你应该是懵逼的,接下来我来解释⼀下这个结果到底是如何运算出来的。
2<<1 :⼗进制“2”转换成⼆进制为“00000000 00000000 00000000 00000010”,再将⼆进制左移⼀位,⾼位丢弃,低位补0,所以结果为“00000000 00000000 00000000 00000100”,换算 成⼗进制则为“4”。(一个数字左移N位相当于乘以2的N次方)。
2>>1: ⼗进制“2”转换成⼆进制为“00000000 00000000 00000000 00000010”,再将⼆进制 右移⼀位,低位丢弃,⾼位补0,所以结果为“00000000 00000000 00000000 00000001”,换算 成⼗进制则为“1" 。(一个数右移N位相当于除以2的N次方)。
对于这两种情况⾮常好理解,那什么是⽆符号右移,以及负数是怎么运算的呢? 我们先来看 -2 > 1 ,这两个负数的左移与右移操作其实和正数类似,都是先将⼗进制 数转换成⼆进制数,再将⼆进制数进⾏移动,所以现在的关键是负数如何⽤⼆进制数进⾏表示。
负数位移运算
我们再来看 -2 > 1 。 -2⽤原码表示为 10000000 00000000 00000000 00000010 -2⽤反码表示为 11111111 11111111 11111111 11111101 -2⽤补码表示为 11111111 11111111 11111111 11111110 -2 << 1 ,表示-2的补码左移⼀位后为 11111111 11111111 11111111 11111100 ,该补码对应 的反码为:
11111111 11111111 11111111 11111100
- 1
= 11111111 11111111 11111111 11111011该反码对应的原码为:符号位不变,其他位取反,为 10000000 00000000 00000000 00000100 , 表示-4。 所以 -2 > 1 是⼀样的计算⽅法,这⾥就不演示了。
⽆符号右移
上⾯在进⾏左移和右移时,有一点需要注意,就是在对补码进⾏移动时,符号位是固定不动的,⽽⽆符号 右移是指在进⾏移动时,符号位也会跟着⼀起移动。 ⽐如 -2 >>> 1 。 -2⽤原码表示为 10000000 00000000 00000000 00000010 -2⽤反码表示为 11111111 11111111 11111111 11111101 -2⽤补码表示为 11111111 11111111 11111111 11111110 -2的补码右移1位为: 01111111 11111111 11111111 11111111 右移后的补码对应的反码、原码为: 01111111 11111111 11111111 11111111 (因为现在的符号 位为0,表示正数,正数的原、反、补码都相同) 所以,对应的⼗进制为2147483647。 也就是 -2 >>> 1 = 2147483647
总结
这⾥总结⼀下,我们可以发现: 2 << 1 = 4 = 2*2
2 << 2 = 8 = 2*2*2
2 << n = 2*2 m << n = m * 2 右移则相反,所以⼤家以后在源码中再看到位运算时,可以参考上⾯的公式。
相关文章:

快速了解原码、反码、补码和位运算
我们知道计算机使用的是二进制,我们⽤⼀个字节,也就是8个bit 来表示⼆进制数。 原码 十进制 原码20000 0010-21000 0010 原码其实是最容易理解的,只不过需要利⽤⼆进制中的第⼀位来表示符号位,0表示正数,1表示…...

算法的复杂度介绍
算法的复杂度介绍 算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别。 为什么要进行算法分析&…...

教你如何搭建店铺—收支管理系统,demo可分享
1、简介1.1、案例简介本文将介绍,如何搭建店铺-收支管理。1.2、应用场景以店铺收支管理为核心,维度数据分析,智能指导门店经营,账目清晰一目了然,店铺经营更高效。2、设置方法2.1、表单搭建1)新建表单【客户…...

java性能分析-堆内存最佳实践-堆分析
堆内存最佳实践 优化垃圾回收器标志参数很重要但是采用更好的编程实践获得更大的性能提升 1.谨慎的创建对象并尽快的丢弃,是更好的内存是提高gc更好的方法 2.频繁创建某种类型的对象会导致整体的性能变差 对象复用设计 线程局部变量 每个线程中创建一个局部变量…...
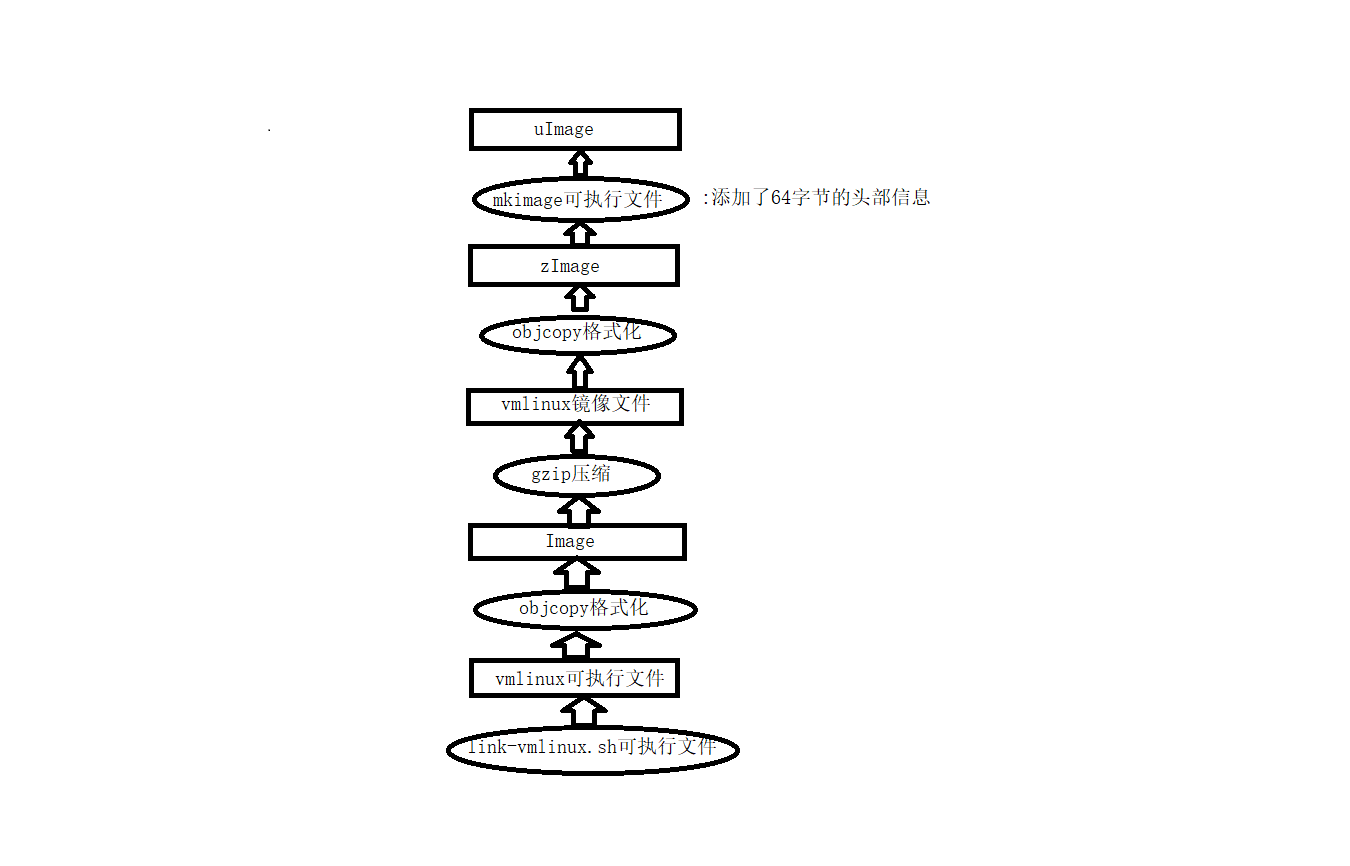
3月8号作业
题目:题目一:vmlinux可执行文件如何产生题目二:整理内核编译流程:uImage,zImage,Image,vmlinux之间的关系答案一:在内核源码目录下vi Makefile,搜索vmlinux目标,vmlinux: scripts/li…...
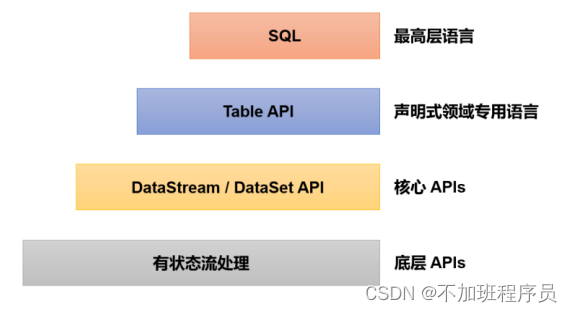
Flink相关介绍
简介 Flink的定位是:Apache Flink是一个框架和分布式处理引擎,如图所示,用于对无界和有界数据流进行有状态计算。Flink被设计在所有常见的集群环境运行,以内存执行速度和任意规模来执行计算。 Flink 框架处理流程应用场景 1、电…...

Java 8 排序
今天分享 Java 8 进行排序的 10 个姿势,其实就是把 Java 8 中的 Lambda、Stream、方法引用等知识点串起来 传统排序 现在有一个 List 集合: public static List<User> LIST new ArrayList() {{add(new User("Lisa", 23));add(new Us…...

Blazor_WASM之4:路由
Blazor_WASM之4:路由 路由模板 通过 Router组件可在 Blazor 应用中路由到 Razor 组件。 Router 组件在 Blazor 应用的 App 组件中使用。App组件模板如下 <Router AppAssembly"typeof(Program).Assembly"><Found Context"routeData"…...

对Vue响应式的理解
1. 啥是响应式? (1).所谓的数据响应式就是能够使数据变化可以被检测到并且对这种变化做出响应式的机制 2. 为什么vue需要响应式? (1).MVVM框架中要解决的核心问题数据驱动视图,数据的改变引起视图的更新ÿ…...

磁盘阵列Raid探讨
最近公司买服务器,顺便了解一下服务器配置方面的问题 以下讨论的都是入门级服务器配置,全部是主观意见,没有任何科学依据,欢迎大家讨论 Raid0,Raid1,Raid10,Raid5,Raid6(Raid5热备)…...

基于MyBatis依次、批量、分页增删改查
我们知道处理数据有三种思路:依次、批量、分页,对应方法如下 依次处理:在 Java 里面写 for 循环,依次使用 SQL 语句,频繁连接断开数据库批量处理:在 MyBatis 里面用 <foreach> 拼接成一条长 SQL 语句…...

Tomcat源码分析-Session源码解析
tomcat session 设计分析 tomcat session 组件图如下所示,其中 Context 对应一个 webapp 应用,每个 webapp 有多个 HttpSessionListener, 并且每个应用的 session 是独立管理的,而 session 的创建、销毁由 Manager 组件完成&…...

常见数据模型
目录 1.1两类数据模型 1.2概念模型 1.3数据模型的组成要素 1.4常见数据模型 层次模型 网状模型 关系模型 数据模型是对现实世界数据特征的抽象,也就是说数据模型是用来描述数据、组织数据和对数据进行操作的。数据模型是数据库系统的核心和基础。 1.1两类数…...

Lesson 8.3 ID3、C4.5 决策树的建模流程 Lesson 8.4 CART 回归树的建模流程与 sklearn 参数详解
文章目录一、ID3 决策树的基本建模流程二、C4.5 决策树的基本建模流程1. 信息值(information value)2. C4.5 的连续变量处理方法三、CART 回归树的基本建模流程1. 数据准备2. 生成备选规则3. 挑选规则4. 进行多轮迭代5. 回归树的预测过程四、CART 回归树…...

阿里云手机短信登录
阿里云短信服务介绍阿里云短信服务(Short Message Service)是广大企业客户快速触达手机用户所优选使用的通信能力。调用API或用群发助手,即可发送验证码、通知类和营销类短信;国内验证短信秒级触达,到达率最高可达99%&…...
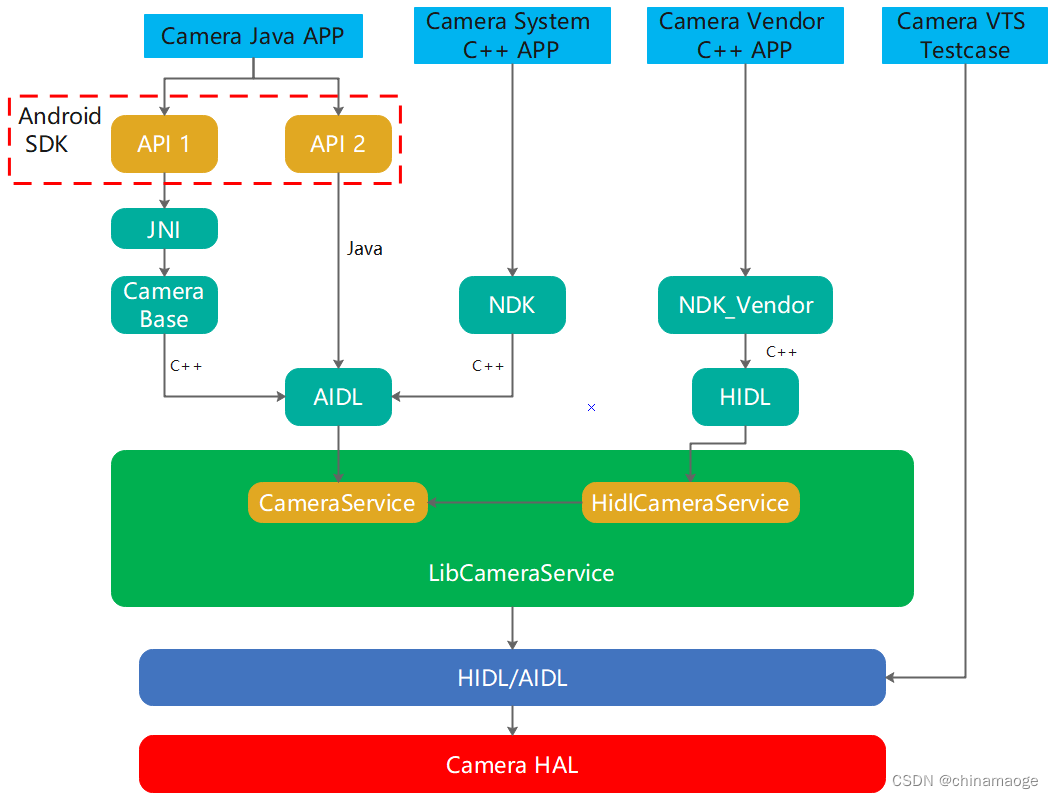
Android Camera SDK NDK NDK_vendor介绍
Android Camera JNI NDK NDK_vendor介绍前言主要有哪几种interface?Android SDKCamera API 1Camera API 2小结Android NDKNDK InterfaceNDK Vendor Interface小结Camera VTS Testcase总结Reference前言 本篇博客是想介绍Android camera从application layer到camera…...

SQL基础语句小结
🍎道阻且长,行则将至。🍓 目录 一、SQL概述 1.简介 2.格式语法 3.SQL分类 二、DDL操作数据库 1.创建数据库 2.查询与使用 3.删除数据库 三、DDL:操作表 (1)数据类型 (2)创建表 (3)查询当前数据库的表 (4)删除表 (5)修改表 四、DML…...

管理类书籍推荐
管理类书籍对于每一位想要获得管理能力提升或者实现职业生涯更上一层楼的企业管理者或领导者而言,都是不可或缺的一项重要学习工具。作为管理工作从事者的职场必需品,一本出色的管理类书籍可以为我们提供大量宝贵的经验与专业建议,从而让管理…...
win10 mingw 调用python
ubuntu调用pythonhttps://blog.csdn.net/qq_39942341/article/details/129333969 我这里mingw是用msys2的 opencv也是msys2装的 安装msys2和opencv可以参考这个https://blog.csdn.net/qq_39942341/article/details/129380197?spm1001.2014.3001.5502 环境变量里加入python路…...

教你使用三种方式写一个最基本的spark程序
当需要处理大规模数据并且需要进行复杂的数据处理时,通常会使用Hadoop生态系统中的Hive和Spark来完成任务。在下面的例子中,我将说明如何使用Spark编写一个程序来处理Hive中的数据,以满足某个特定需求。假设我们有一个Hive表,其中…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...
